轴承测量仪圆度测量误差分析及调整

杨泳烽

(新昌皮尔轴承有限分司 浙江 新昌 312500)

在轴承加工过程中,对圆度的控制通常采用两种方法,一种是利用轴承测量仪对圆度值进行估算,另一种则是通过圆度仪进行测量。其中，利用轴承测量仪进行圆度估算在生产应用中极为广泛,但得到的估算值只是一个近似值,而圆度仪测量采用的是符合圆度定义标准的计算方法,因此,采用这两种方法所得到的测量值都存在着一定的误差。特别是在实际工作中,针对同一个产品采用两种方法所得到的测量值相差很大,有时甚至会怀疑测量方法的正确性。因而,需要对轴承测量仪测量圆度误差的方法进行分析和研究,找出改进的办法,以消除这种误差。

1 反映系数推导

1.1 圆度误差富氏级数

圆度误差富氏级数表达式为

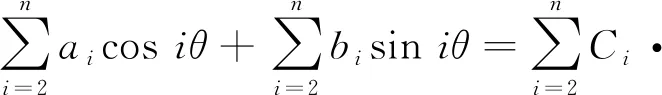
cos (iθ+iφ),

(1)

1.2 圆度误差与反映系数

反映系数反映了测量值对真实圆度误差值的放大或缩小程度，即

Kn=S/Δr,

(2)

式中：下标n为谐波数；S为量表指针最大值与最小值之差；Δr为实际圆度误差值。结合(1)式可得

利用图1所示结构及产品测量时各支承点对量表的反应值变化，并依据(1)式，可以推导出反映系数Kn的函数表达式[1]为：

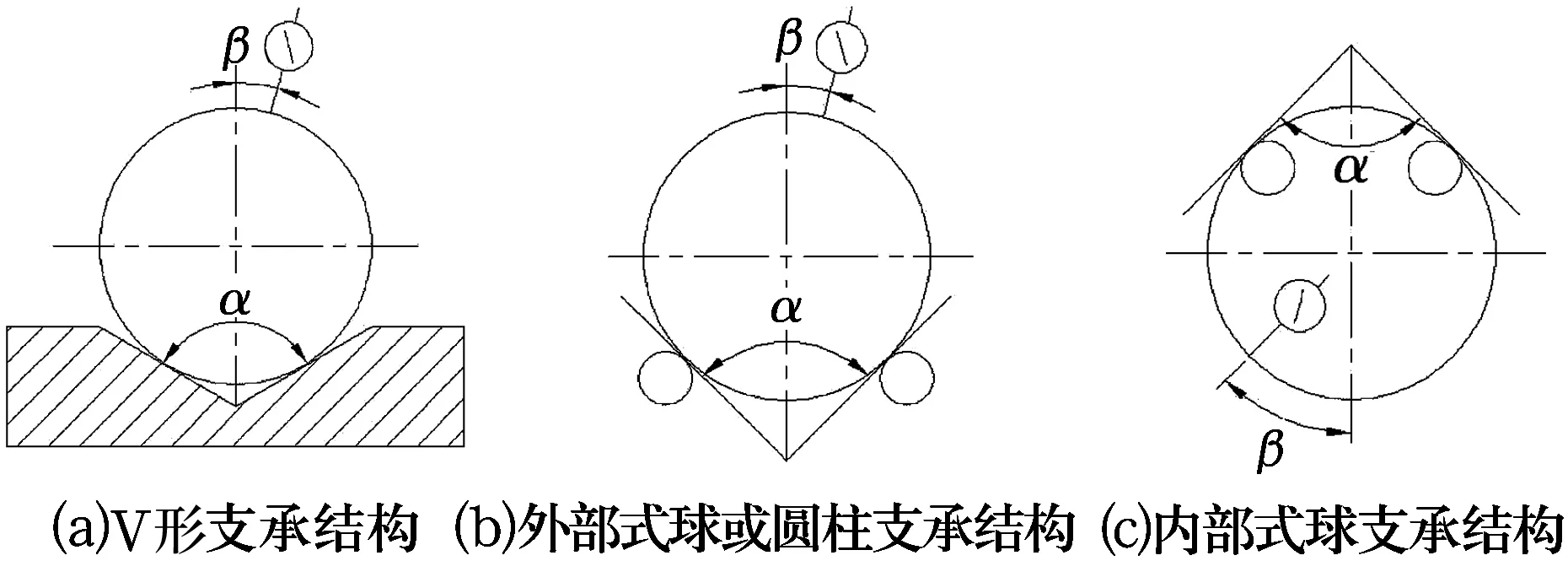
图1 支承结构类型

图1所示α为测量支承夹角，β为量表测量角，即测量方向与测量支承夹角平分线之间的角度。从 (3) 式可得，当产品棱数确定时，α和β角将决定反映系数Kn值，最终影响圆度测量结果。

2 轴承测量仪结构及调整的误差分析

根据图1所示的3种不同结构类型，结合实际工作中常见D022,D923A,D012及D913A轴承测量仪，对其结构类型进行分析，并根据这4款轴承测量仪现有调整方式所得到的α和β，分别进行产品圆度测量误差的分析，并提出调整方法。

2.1 D022轴承测量仪

D022轴承测量仪采用的是顶式非对称三点测量,其结构类型与图1b所示结构一致，两支承理想夹角成90°，并可通过导槽进行上下调整，因此α和β角会因为支承的调整高度以及两支承的平行度而发生变化，调整状态如图2所示。若测量同一产品，当两支承的高度改变时,支承与产品的公共切线会发生旋转和偏移,因此，在实际调整过程中，可将指向端面的表针作为参照调整支承高度，以有效控制α角的一个变动范围。以测量内圈沟道直径D=50 mm的产品为例，采用直径d=6 mm的钢球支承(即轴承测量仪上的定位支点)，通过目视控制的办法，支承调整时偏离理想高度可在±1.5 mm范围内等概率分布，则可利用以下公式计算出因支承调整误差所引起的α角的变动范围。

1—导槽；2—支承垫块；3—钢球支承；4—测量产品；5—侧导槽；6—量表

(4)

(5)

式中：L为α=90°时理想支承的中心距；Δh为支承高度调整误差，即调整偏离量；α′为需计算的变动后的α值。

根据已知条件可计算得到上述α角的变动范围为80°≤α≤90°。当两支承之间的平行度发生变化时,支承夹角的中心线也会发生旋转和偏移,但由于尺寸量表可在与水平成135°的方向上进行调整，通过产品中心并能找到最大值，因此，β角的变动范围也可计算求得。以上例为相同条件,对单面支承偏离理想高度±1.5 mm进行计算，得

(6)

得到β角的变动范围为42°≤β≤48°。根据α和β角的变动范围以及(4)式,可对D022轴承测量仪进行变动范围内圆度误差反映系数的分析。

从表1中分析得到，D022轴承测量仪测量圆度误差时对偶次棱状产品的反映较为明显，而对于奇次棱状产品，反映系数较小，因此，量表对于圆度误差的反映很小或没反映。只有当两支承与产品接触点的公共切线相互垂直时，得到的才是偶次棱状产品较为准确的圆度值，虽然这适用于偶次棱状产品，但并不符合圆度所定义的范畴。因此，D022轴承测量仪可以通过调整两支承的高度位置，使支承夹角α和测量角β发生变化，改变反映系数Kn，利用组合测量[2]的方式得到较为准确的圆度值。测量方案如表2所示，在实际调整前，应根椐选择方案的α和β计算出相对应的调整距离和高度。

表1 反映系数Kn调整误差变动量

表2 DO22轴承测量仪组合测量调整方案

(7)

(8)

式中：h为支承垫块高度。调整时可先根据计算得到的支承距离，利用量具或相同尺寸的卡具在相等高度上对支承进行定位，并根据计算结果，利用垫块垫高支承。

2.2 D923A轴承测量仪

D923A轴承测量仪采用顶式非对称三点测量，其结构类型与图1c所示结构一致，调整时可如图3所示。

两支承可分别沿导槽两个相互垂直的方向进行移动调整，支承夹角可随着支承位置的移动而改变即图3中α变为α′，但由于受到导槽方向限制，无法调整量表通过产品最大直径，因而也就无法相应的调整β角。而在实际调整时，量表及同一方向导槽内支承需通过产品最大直径，而另一支承则由于受到导槽可移动方向及产品直径的制约，其调整位置相应固定，所以，每次调整都可以得到相同的支承夹角α=90°及量表角度β=45°，并根据(3)式求得相应棱数产品的反映系数，即产品为偶次棱数时反映系数Kn=2。因此，D923A轴承测量仪由于受β角调整制约，无法满足产品圆度的组合测量方案要求，则只能在已知产品棱数为偶数情况下，才能较为准确地测量出产品的圆度值，而对于奇次棱数产品，由于反映系数无法确定，在各产品棱数相等的情况下，其圆度测量误差也各不相同。

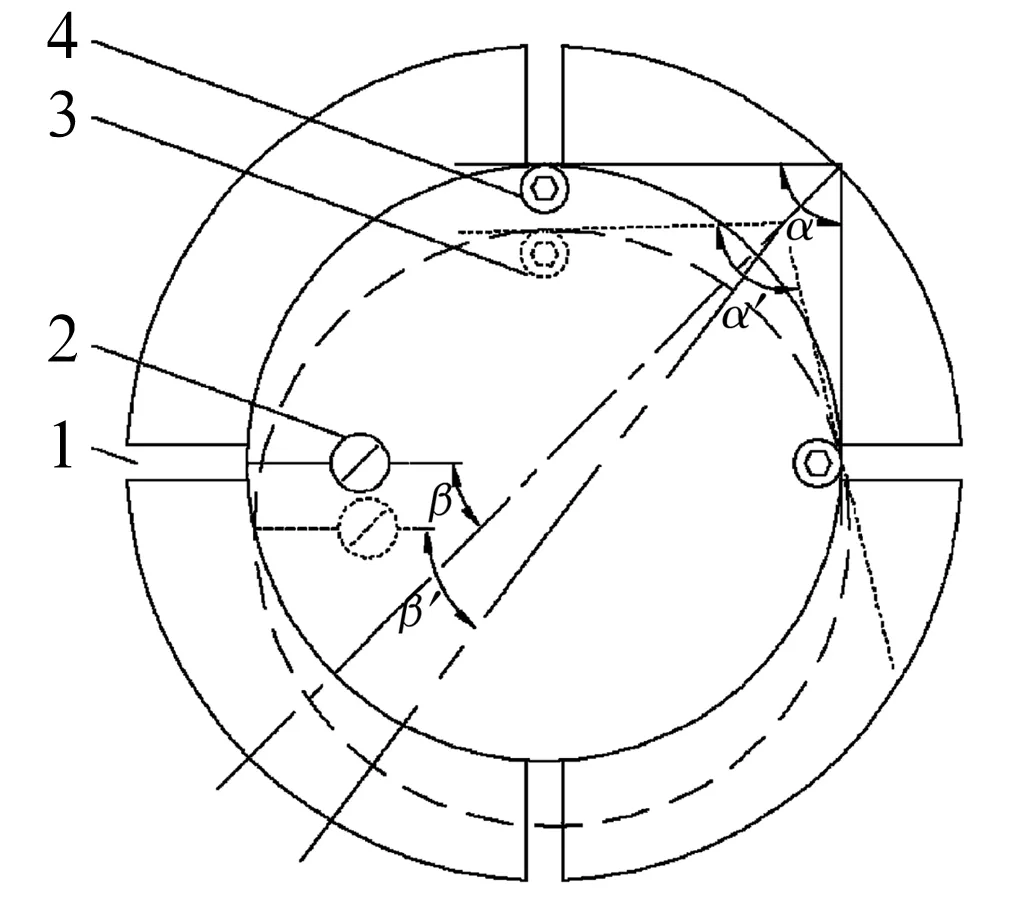
1—导槽；2—量表；3—移动调整后支承；4—移动调整前支承

2.3 D012轴承测量仪

D012轴承测量仪采用顶式对称三点测量，结构类型与图1c所示结构一致，支承调整时，以目测方式旋转并调整两定位钢球支承高度及产品的测量接触点，使支承夹角α=90°，并同样以目测方式旋转并调整量表支承与产品的测量接触点，使量表角度β=0°。由于受目测调整偏差的影响，两定位钢球支承高度以及两定位钢球支承与产品测量的接触位置会存在一定的差异，再加上量表支承测量接触点的调整偏差，则量表支承测量方向与测量支承夹角平分线之间就会产生一定的偏离，而受到量表位置调整限制，无法对β角进行调整，也就得不到相应的反映系数。若假设支承调整为理想结构时，即=90°，β=0°，则可利用(3)式求出相应的反映系数，如表3所示。

表3 D012轴承测量仪理想结构圆度测量的反映系数Kn

从表3可以看出，该调整结构对于不同棱数产品之间的反映系数差异较大，如4，12棱数产品测量时，其圆度对于量表的反映将可能变的很不明显，所以，在产品棱数未知的情况下，圆度值是很难进行判断的。而在实际调整时，由于该轴承测量仪的可调整结构无法满足组合测量方案，再加上支承调整偏差而可能引起的量表测量角的偏离，因此，产品棱数无论是在已知或未知情况下，都无法得到准确的圆度测量值。

2.4 D913A轴承测量仪

D913A轴承测量仪按其结构和调整方法，既可用顶式对称三点测量，也可用顶式非对称三点测量，如图4所示。

1—平板；2—45°导槽；3—支承；4—测量产品；5—量表

图4a，4b为顶式非对称三点测量，实际调整时，支承的位置随着产品尺寸的大小而进行调整，其α和β角都会发生变化，因此，对于各个产品圆度的反映系数差别较大，在产品棱数未知及反映系数未能确定的情况下评定圆度误差是不正确的。但当支承和产品的公共切线与45°导槽垂直或支承与量表方向垂直且通过产品中心时，对于偶次棱状产品的反映系数为2，可以容易控制产品圆度，但仍无法反映全部的圆度误差。通过组合测量的方式，在产品棱数未知的情况下可以较为准确地计算圆度误差值，具体方案如表4所示。

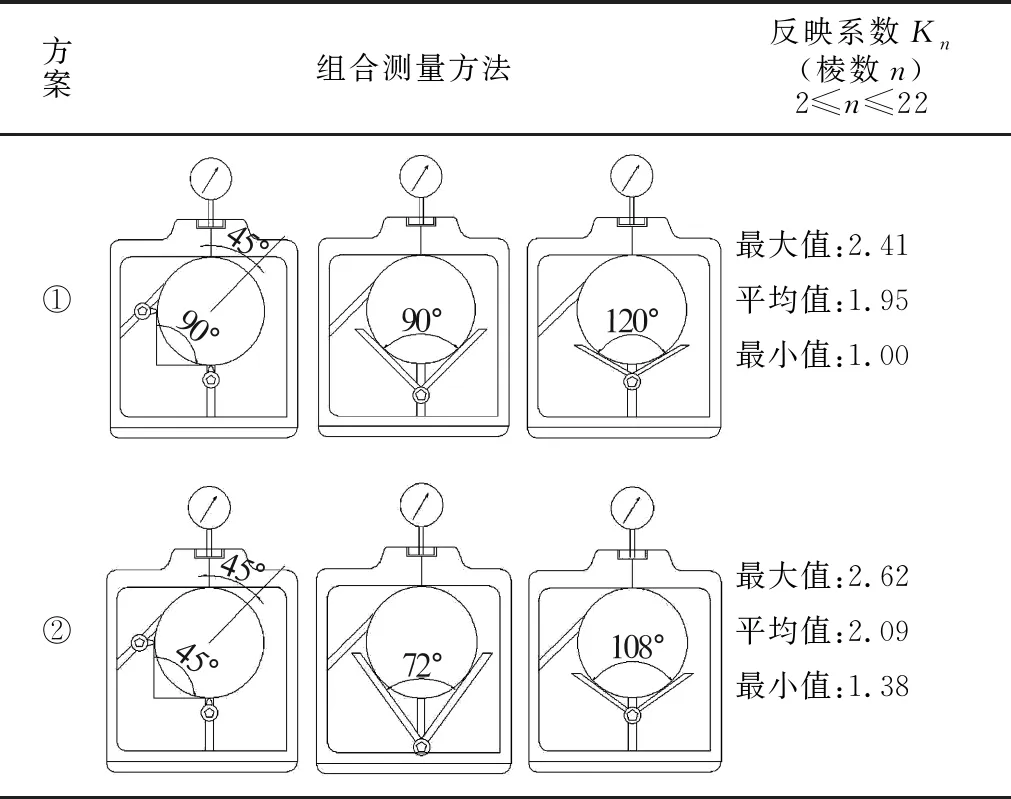
表4 D913A轴承测量仪组合测量调整方案

3 组合测量方案与圆度仪测量值对比

根据以上对D022及D913A轴承测量仪所提出的组合测量调整方案，分别进行调整，并利用Taylor圆度仪与该组合方案分别对同一内、外圈产品进行圆度测量，得到测量结果如表5所示。

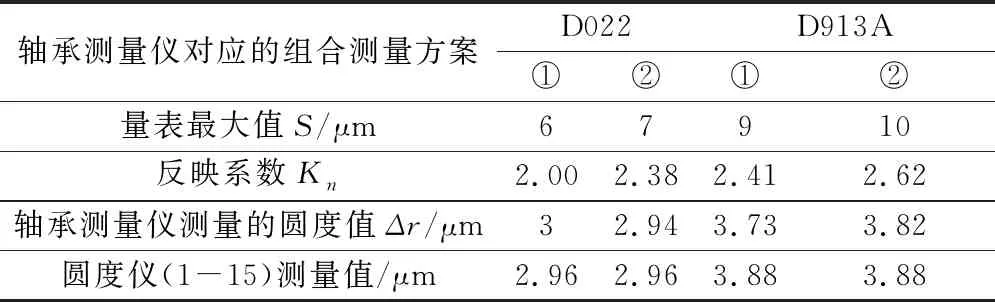
表5 组合方案与圆度仪测量值对比

4 结束语

通过对以上几种轴承测量仪圆度测量的误差分析得到，影响误差的主要因素是其支承与量表的调整结构以及调整时所出现的偏差。由于实际测量时，棱数都是为未知的，则只能通过组合测量方案的调整才能最大程度消除误差，并且通过对比试验结果可以看到，采用这种方法所得到圆度值与符合圆度定义标准的圆度仪测量值非常接近，完全可以满足圆度测量控制的要求。