汽车水泵轴承密封圈接触应力有限元分析
周琼,李正美,唐建平,徐泽民,安琦
(1.华东理工大学 机械与动力工程学院,上海 200237;2.江苏容天乐机械股份有限公司,江苏 常州 213000)
带骨架的唇形密封圈是汽车水泵轴承的关键部件,具有双重作用:一方面避免润滑脂的泄漏及对整个系统的污染;另一方面防止外界的水以及灰尘等杂物侵入轴承内部,避免轴承内润滑油的污染失效,从而维护轴承的正常运转。
汽车水泵轴承为接触式密封,轴与密封唇的接触保持一定的过盈量,可产生一定的接触密封压紧力。如果过盈量过大,会导致过大的摩擦发热,降低密封圈的使用寿命;过盈量过小,会使密封压力过小,密封效果差。可见,密封圈密封性能的好坏在很大程度上取决于过盈量的大小。目前国内、外汽车水泵轴承密封圈的过盈量主要依靠经验选取,不能满足现代精确设计的要求[1-3]。为此,以某公司生产的WR3258152型汽车水泵轴承密封圈为研究对象,利用ANSYS建立密封圈的有限元模型,对接触宽度上的唇口接触应力及其分布进行分析,以研究接触过盈量对接触应力大小的影响规律,为汽车水泵轴承密封圈的设计及优化提供借鉴。
1 密封圈有限元模型
1.1 几何模型
汽车水泵轴承密封圈为圆环体,其边界受力条件具有圆周对称性,结合ANSYS软件的功能,密封圈可简化为二维轴对称模型。该二维轴对称模型如图1所示,δ为密封圈主唇口初始过盈量。这种简化能在很大程度上减少建模及分析的时间,同时不会影响分析结果。

1—轴;2—第2唇;3—骨架;4—主唇
采用三节点的自动网格划分功能对密封圈进行网格划分,由于主要对密封唇部与轴之间的接触应力及其分布进行分析,故对唇部进行网格细化(图2),从而能使计算结果更加精确。
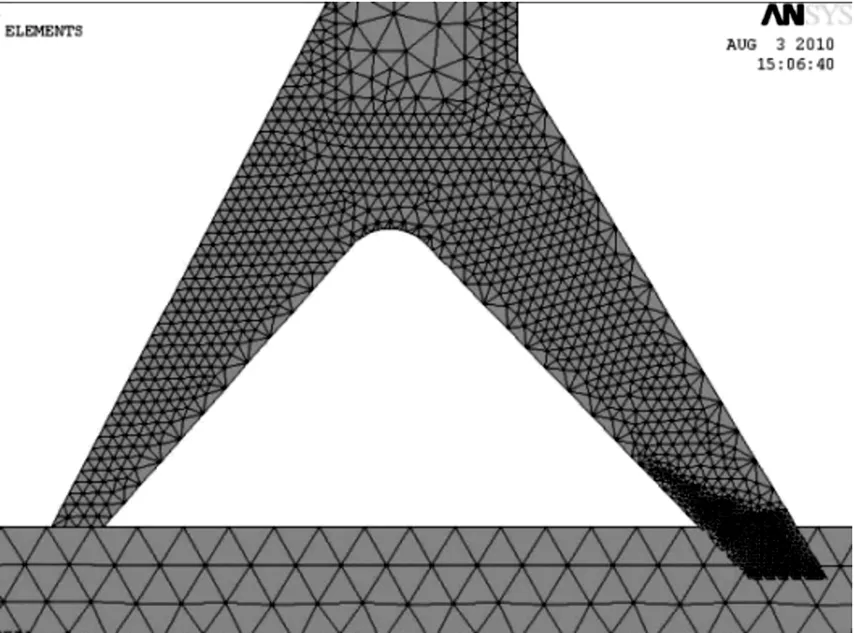
图2 密封圈的有限元模型
1.2 密封圈材料的有限元模型
密封圈材料为氟橡胶。橡胶材料为非线性超弹性材料,受载后表现出大变形,而密封圈中的钢骨架为小变形,这样使得密封圈变形成为复杂的非线性问题,其中包括材料非线性、接触非线性和结构非线性(大变形)[4]。
在橡胶密封圈有限元计算中,材料的应变能函数,即应力应变关系是必不可少的,用Mooney-Rivlin模型[5]可以较好地描述橡胶类不可压缩超弹性材料在大变形下的力学特性,其应变能密度函数为
W=C1(I1-3)+C2(I2-3)+k(I3-1)2/2,
(1)
式中:Ii为第i方向的应变不变量,i=1,2,3;k为体积弹性模量;C1和C2为待定的Mooney-Rivlin常数,根据文献[6-7]中橡胶材料系数的确定方法取C1=1.25,C2=0.313。对不可压缩的超弹性体,I3=1,则(1)式可简化为
W=C1(I1-3)+C2(I2-3)。
(2)
橡胶材料在受力下表现为大位移和大应变,可用大应变理论进行研究,且不采用一步直接求解的方案,而采用增量求解法和完全拉格朗日公式[8]求解。首先,将载荷分成若干级逐步加载,然后按各个阶段不同的非线性特性逐步求解。实质上是把一个复杂的非线性加载过程,分割成若干个非线性程度较轻的加载小段,分别对每一小段迭代求解,这样可避免非线性方程求解过程中较严重的发散现象。其次,将整个物体离散化后,采用全拉格朗日法以未变形时(或某一基准时刻)结构构形为参照构形,推导出非线性平衡方程为
([tK]L+[[tK]NL){uk}={t+ΔtR}-{tF},
(3)
式中:[tK]L为线性总体刚度阵;[tK]NL为非线性影响刚度阵,反映应变位移中非线性部分对刚度阵的影响;uk为节点位移增量;t+ΔtR为t+Δt时刻的外载荷阵列;tF为t时刻物体原有的应力引起的等效节点力阵,也称初应力影响项。
接触问题的复杂性是由于接触前、后系统状态的改变及接触边界条件的高度非线性所引起,正确处理接触问题是计算成功的关键。汽车水泵轴承密封圈和轴的接触属于柔性体与刚体的面面接触。有限元分析中,密封圈和轴可抽象为轴对称问题,密封圈作为接触体, 轴为目标体。由于密封结构中同时存在几何、材料及结构非线性,这里采用接触单元的罚函数算法进行分析。当物体接触时,单元具有一定的刚度,可阻止物体接触边界的相互嵌入;当物体脱离开时,接触单元的刚度为零,对物体的变形没有任何约束。从变分的角度看,是将结构的总势能π表达为应变势能W、外力势能We和接触势能Q之和[9],即
π=W+We+Q,
(4)
通过罚单元给出Q的表达式,从而可以解决接触面不被穿透的问题。
1.3 边界条件
由于密封圈的第2唇在接触过程中变形很小,只研究密封圈主唇的过盈量产生的接触应力及其分布,即对密封圈进行静态分析。密封圈外径面与轴承外圈密封槽过盈配合,为提高计算效率,建模时将密封圈外径面所有自由度进行约束即可,无需建立外圈钢筒模型。同时,由于骨架和轴的刚度相对橡胶密封唇很高,这里不考虑接触过程中骨架和轴的变形影响,即约束其所有自由度。
2 数值模拟结果及分析
当汽车水泵轴承密封圈安装后,唇口受到压缩,以初始过盈量δ=0.2 mm为例,密封圈变形及Von-mises应力分布如图3所示。可见密封圈与轴配合后主唇有明显的翘起,与轴表面形成线接触。变形和应力分布主要集中在唇口和主唇上,与实际情况相符。
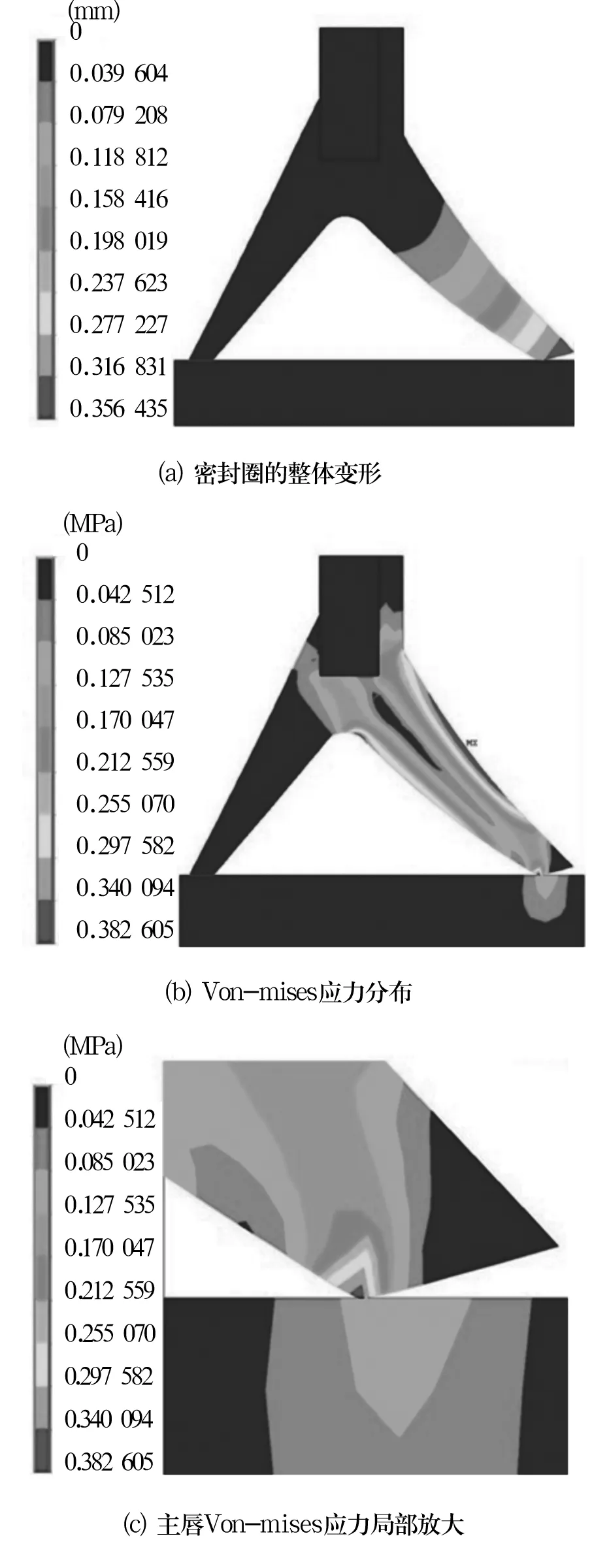
图3 δ=0.2 mm时密封圈的变形及Von-mises应力
图4表示的是密封圈主唇口接触应力分布,可以看出密封圈的接触应力呈三角形分布,且接触应力的峰值几乎在接触面宽度的正中间,这样的接触应力分布对密封圈的疲劳寿命是不利的。因此,根据分析,在后期密封圈的改进过程中可以改变唇口接触尖角结构,使其具有一定的圆角弧度,以改善唇口接触应力分布,从而提高密封圈的接触疲劳寿命。

图4 δ=0.2 mm时密封圈接触宽度上的接触应力分布曲线
目前汽车水泵轴承密封圈主唇口的初始过盈量一般为δ=0.1~0.2 mm,这里研究了δ=0.05 ~ 0.20 mm时密封圈主唇口最大接触应力的变化规律。用有限元分析软件分别计算此区间内各个过盈量下的最大接触应力,结果如图5所示,取步长为0.01 mm。
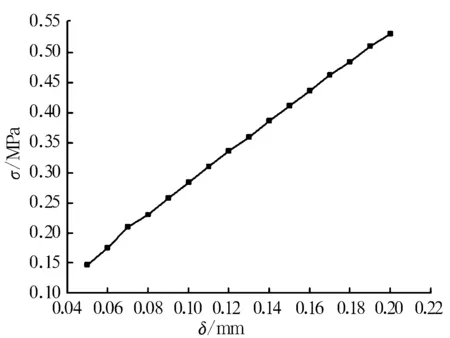
图5 密封圈与轴的接触应力随过盈量的变化规律
由图5可见,密封圈与轴接触面间的接触应力随初始过盈量的增加而增大,呈近似线性关系。接触应力增加会提高密封压力,增加密封效果;但过盈量增加也会使唇口与轴之间的压紧力增大,摩擦力增大,进而使摩擦发热增加,磨损加剧。因此,初始过盈量的选择对密封圈的密封性能有着至关重要的影响。
3 结论
(1)汽车水泵轴承密封圈主唇口沿轴线方向接触宽度上的接触应力呈三角形分布。
(2)汽车水泵轴承密封圈与轴接触面间的最大接触应力与过盈量之间呈近似线性关系。

