高职建筑专业微积分教学策略研究*

庞 杰1徐 伟1殷堰工2（1.苏州建设交通高等职业技术学校 江苏 苏州215104;2.苏州市教育科学研究院 江苏 苏州215004）

高职建筑专业微积分教学策略研究*

庞 杰1徐 伟1殷堰工2
（1.苏州建设交通高等职业技术学校 江苏 苏州215104;2.苏州市教育科学研究院 江苏 苏州215004）

高等职业学校中微积分课程教学状况令人堪忧，许多数学教师“本本主义”的教学倾向较严重，本文结合建筑专业课的教学探讨了微积分课程的教学策略。

高职；建筑专业；微积分教学；数学思想

高等院校微积分课程的任务是:一方面使学生进一步学习和掌握本课程的基础知识和基本能力;另一方面要为学生学习专业课程提供必需和够用的工具，使他们具有学习专业知识的基础和计算能力。然而，高职微积分课程的教学现状令人堪忧，具体表现为学生学习微积分的兴趣低下，没有体会到微积分的应用价值，高职建筑专业微积分的教学状况亦是如此。

高职建筑专业微积分教学存在的问题

我们课题组从微积分的教学内容，教师的教学，学生的学习，与专业课的衔接四个维度进行了调查研究。

高职微积分的教学内容 微积分是微分学和积分学的统称，主要以动态的、变化的、无限的观点来研究问题，本身具有一定的难度。现行的高职微积分教材大多用ε-δ语言进行陈述，逻辑非常严谨，但过于抽象，学生难以理解掌握。

高职教师的教学 通过对数学教师的听课以及问卷调查，我们发现受传统教学观念的影响，许多职业学校教师注重书本知识的理论教学，严格按照教材编写的严密体系实施教学，数学教师努力以数学系的标准来培养高职学生。调查还发现，相当一部分教师为提高学生成绩，把主要精力放在形式化的计算上，对微积分中蕴涵的重要思想方法却一带而过。

高职生对微积分的学习 高职生由于生源质量偏低，数学基础较差，对微积分的学习困难较大。并且高职学生对学习微积分的目的、意义认识不够，学习态度不端正，劲头不足。在对个别学生进行的访谈中，我们得知许多学生认为学习微积分没什么用，跟专业课没什么关系，只要学好专业课就行了。

微积分课程与建筑专业课程的衔接 我们对建筑专业课教师进行了访谈，他们认为建筑专业很多地方都用得到微积分，而且数学教师对微积分的教学内容讲得还不够深入，例如，曲面积分就没有讲，他们要用曲面积分时，学生根本不会用。为此，我们课题组挑选了一些建筑专业课教材进行浏览，发现建筑专业课程中有许多内容涉及微积分的知识，可以说建筑力学和弹性力学是以微积分知识为基础才能学习的。

高职建筑专业微积分教学存在问题的原因

建构主义认为，知识不是通过教师传授的，而是学习者在一定的情境即社会文化背景下，借助其他人（包括教师和学习伙伴）的帮助，利用必要的学习资料，通过意义建构的方式而获得的。建构主义要求教师帮助学生对当前学习内容所反映的事物的性质、规律以及该事物与其他事物之间的内在联系达到较深刻的理解。因此，高职数学教师要关注学生的知识层面，学生学习联系生活实际，数学课堂教学才有意义。

荷兰数学家弗赖登塔尔提倡“现实数学”的教育思想，即数学教育要联系学生的两个现实，客观现实和数学现实，让学生看到数学是有实际意义和学习价值的。他认为数学教育的任务就是要充分利用学生的客观现实，不断丰富和扩展学生的数学现实。高职院校建筑专业学生的客观现实和数学现实就是他们的建筑专业课。因此，数学课的教学要与专业课衔接和渗透起来，才能达到最优的教学效果。

高职建筑专业微积分教学策略

实际上，抽象化、严密化的微积分在创立之初并非如此。微积分是微分学和积分学的统称。积分学源自曲线的长度、区域的面积、物体的体积的计算方法。古希腊的Eudoxusde的穷竭法和Archimedes的平衡法，中国魏晋时期刘徽的割圆术和祖冲之的圆周率计算以及求体积的原理都涉及积分学。微分学的起源比积分学晚。它主要源自求曲线的切线、运动物体的瞬时速度、一些极大极小值的问题。Newton和G.W.Leibniz建立了微积分基本定理，创立了微积分。创立之初的微积分是不严格的微积分，然而正是这样的微积分所蕴含的思想对微积分的应用产生了深远的影响，为此本文提出以下教学策略：

重视微积分思想的教学 在历史发展进程中，微积分不是一下子就严谨精确的。例如，导数概念的发展，导数引入之初，Newton指出:“两个量之比，如果在有限时间内不断趋于相等，且在这一时间终止前互相靠近，使得其差小于任意给定的差别，则最终就成为相等。”这个定义实际上是导数为变化率极限的直观描述。因此就可以用这个直观概念对导数概念的课程教学内容进行设计。

人们通常所说的物体作直线运动的速度，是指在一段时间内物体运动的平均速度，在客现实际中，仅知平均速度是不行的，还必须知道它在每一时刻的瞬时速度。已知自由落体的运动方程为S=gt2，试讨论落体在时刻t0=1秒时的瞬时速度。为此，可取一邻近于t.=1秒的时刻t，并求出落体由1秒到t秒，这一段时间内的平均速度。

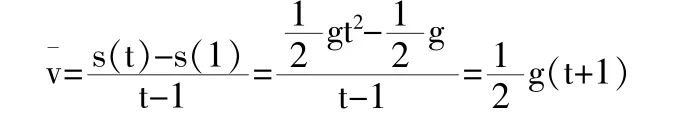
具体说，如t=1.5秒时，落体在1秒到1.5秒之间的平均速度是v

t=1.1秒时，落体在1秒到1.1秒之间的平均速度是v¯[1，1.1]=

t=1.01秒时，落体在1秒到1.01秒之间的平均速度是v¯[1，1.1]

由此可以推断，落体在t0=1秒时的瞬时速度，为趋近的值v

这样的教学设计是从导数起源思想出发，较直观贴近生活实际，高职生较易理解、掌握。

避免冰冷、抽象的教学方式 在Newton和G.W.Leibniz建创立微积分之后，一批伟大的数学家A.L.Cauchy，G.Cantor对微积分进行了严谨化的工作，而严谨的ε-δ定义则是由大数学家K.T.L.Weierstrass给出的，使微积分朝着精确化、严格化的方向发展。同时，微积分的表述方式也变得愈加冰冷和抽象。以至于一些高职微积分教科书亦采用严格化、精确化的方式表述。我们同样以导数的概念为例。有些高职微积分教科书采用下列方式直接引入导数概念。定义：设函数y=f（x）在x0的某个邻域内有定义，当自变量x在x0处有增量x时，函数y有相应的增量；△y=f（x0+△x）-f（x0）;如果当x→0时，的极限存在，则称函数y=f（x）在点x0可导，这个极限的值较函数y=f（x）在点x0的导数，记为f'（x0），f'（x0）或之后，再引入导数的几何意义——切线斜率。这种教学方法过于抽象，脱离现实生活，学生难以理解和掌握。

高职微积分教学与专业课相结合 建筑专业课程中有许多内容涉及微积分的知识，甚至建筑力学和弹性力学是以微积分知识为基础，根据弗赖登塔尔的教学思想，微积分的教学要与专业课衔接和渗透，才能达到较好的教学效果。本文以导数的概念教学为例，来说明微积分教学和建筑专业课的结合策略。建筑力学中有一个概念称作应力，应力是指内力在构件横截面上的密集程度。例如两根材料相同、横截面的面积不同的杆，受同样大小的轴向拉力P，随着拉力的逐渐增大，截面面积小的杆件必然先断。

为了说明截面上某一点K处的应力，可先围绕K点取一微小面积△A，作用在微小面积△A上的内力为△P，那么比值称为作用在微小面积△A上的平均应力。当内力分布不均匀时，平均应力pm的值将随着△A的大小而变化，不能准确地反映K点处内力集度。只有当△A无限趋近于零时，平均应力pm的极限值p才能代表K点的内力集度，用公式表示为，p称为K点处的应力。实际上，应力是内力对微小面积变化率的极限，数学教师可以在讲述导数的概念之后，结合应力加深学生对导数的概念的理解。

此外，高职微积分与建筑专业课的衔接还可以采用数学建模的方法，针对高职生的学习特点还可以采用小步子，快节奏，精讲多练的方法，这也是我们课题组下一步研究的主要内容。

[1]何小亚.高中数学新课程微积分的课程设计分析[J].数学通报，2006，（4）：9-12.

[2]何克抗.建构主义——革新传统教学的理论基础 （三）[J].学科教育理论研究，1998，（5）：24-28.

[3]张奠宙，林永伟.关于“现实数学”和“数学现实”[J].数学教育学报，2008，（4）：1-4.

[4]梁春光.建筑力学[M].武汉：武汉理工大学出版社，2007.

庞杰，硕士，苏州建设交通高等职业技术学校讲师，主要从事数学教法研究。

徐伟，苏州建设交通高等职业技术学校副教授，主要从事基础数学及数学教育研究。

殷堰工，苏州市教育科学研究院副教授，苏州大学兼职硕士研究生导师，主要从事基础数学及数学教育研究。

G712

A

1672-5727（2011）09-0120-02

*本文系苏州市教育科学“十一五”规划课题《高职校微积分课程与建筑专业课程的衔接和渗透》（课题编号：090104325）的部分成果