NURBS方法的深V型三体船稳性

胡开业，卢友敏，2，丁勇

(1.哈尔滨工程大学多体船国防重点学科实验室，黑龙江 哈尔滨150001;2.武昌船舶重工有限责任公司潜艇设计工艺所，湖北武汉430060)

近年来，以三体为典型代表的多体船型引起了人们广泛关注［1］.三体船兴波阻力较小，两个片体不仅可以增加稳性，横摇时还可以增大横摇阻尼，具有优良的耐波性能［2］.在稳性计算方面，传统的稳性计算是基于型值表的二维数值积分，输入量大，步骤繁复，并引入各种假设，计算精度和效率不高.与单体船相比，三体船与波面的交点较多，情况复杂，需要编制专门的三体船稳性计算程序.另外，在进行三体船稳性分析时通常将片体作为附体计入，事实上虽然片体所占排水量比例不大，但是由于其位置距船体纵中面较远，片体对稳性的影响不容忽略.

深V船型是国际上近几十年来开发的一种新的高速船型［3］，这种船型的突出优点是在汹涛中的耐波性能较常规圆舭船型有较大改善.目前对三体船型的研究主要集中在常规圆舭型三体船型方面，而对深V型三体船的研究确相对较少，鉴于深V船型优良的总体性能，有必要开展深V型三体船型性能的研究.

本文开发了一种基于NURBS技术的深V型三体船稳性计算程序:采用NURBS方法对深V型三体船曲面进行拟合，并在此基础上计算任意倾斜姿态下船体的几何要素和三体船稳性，并讨论不同的船体形状和片体要素对其稳性的影响.

1 计算模型

1.1 NUBRS 相关原理

NURBS方法是计算机曲面造型技术中的重要方法［4］，能够实现二次解析曲线曲面和自由曲线曲面的统一，特别适用于复杂的船体曲面造型［5-6］，因此基于NURBS方法的自由曲面和曲面体的几何特性计算为三体船的稳性计算提供了更为便捷的处理思路和方法，可在三维曲面表达的基础上，直接对深V型三体船进行整体处理和计算.

NURBS曲线为一分段的矢值有理多项式函数，其表达式为

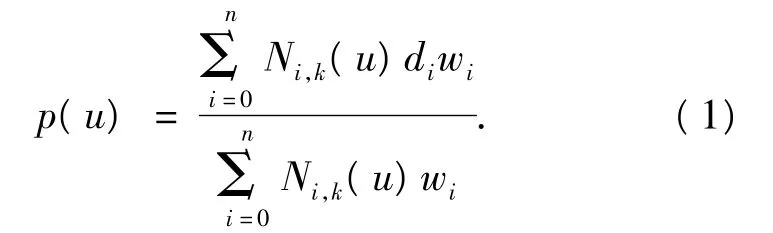
式中:p(u)为参数船体曲面上的点，di为控制顶点，wi为权因子，Ni，k为 k次样条基函数，由递推公式定义，u为节点，由其形成节点矢量U.

NURBS曲面有3种等价表示形式，其中较常用的一种有理分式表示为

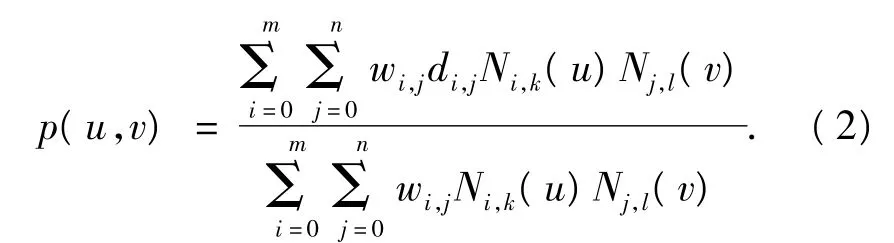
控制顶点 di，j(i=0，1，…，m;j=0，1，…，n)呈拓扑矩形阵列，形成一个控制网格.wi，j是与顶点 di，j联系的权因子，规定四角顶点处用正权因子即w0，0，wm，0，w0，n，wm，n＞0，其余 wi，j≥0 且顺序 k × l个权因子不同时为零.Ni，k(u)和 Nj，l(v)分别为 u 向 k 次和v向l次的规范B样条基，它们分别由u向与v向的节点矢量U=［u0u1… um+k+1］与V=［v0v1… vn+l+1］按德布尔递推公式决定.

本文使用到的NUBRS相关技术主要包括:

1)升阶:主要用于构造组合曲线，对直线段和二次曲线升阶，使其与自由曲线的幂次相同而不改变其形状，计算公式为

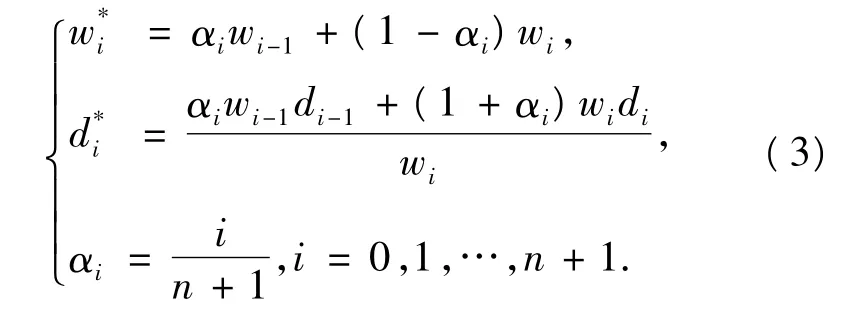
式中:di和d*i分别为升阶后的控制顶点，wi和w*i为升阶前后的权因子.

2)节点插入与删除.用于曲线分段的构造和局部修改，对于不同的曲线插入节点以获得相同的节点矢量，删除节点为插入节点的逆运算，其删除节点的次数应小于曲线的重合度与曲线次数.

3)蒙皮法拟合曲面.先沿某一方向譬如v方向进行，以所给v参数值对v向的m+1个控制多边形及其联系的权因子执行用于计算NURBS曲线上点的算法，求得m+1个点及其权因子作为中间顶点及其权因子，然后以所给u参数值对这些中间顶点及其权因子执行用于NURBS曲线上的算法，所得一点即为所求NURBS曲面的点.

1.2 NUBRS曲面表示与网格划分

船体曲面几何表示方法通常可以分为2种:1)由曲线方程表示，由一组按某种规律变化的平行平面曲线(如横剖线、水线)构成;2)直接用曲面方程来描述船体曲面，如利用Bezier曲面，则需要将船体曲面分成几块曲面片，然后按照位置连续、切平面连续条件拼接得到船体曲面.由于曲线方法是用某些函数来表达型线，和用样条来表达型线相比在控制线条上的拐点数、拐点位置、曲率均匀变化和UV度变化等方面易于控制.本文先采用第一种方法，即在型值表基础上生成曲线，然后由曲线生成NUBRS三维曲面模型.

在船舶型线设计等工程实际中，通常给出有限的离散坐标点，据此构造出所需曲线，即根据已有的型值表，通过定位于曲面上的一些点，对边界条件进行设置，进行插值和相应的变换处理.并根据需要，沿船长和型深方向划分确定合适的网格步长或网格数目，对船体进行横向和纵向加密以生成插值点，建立起曲面控制网格，见图1.

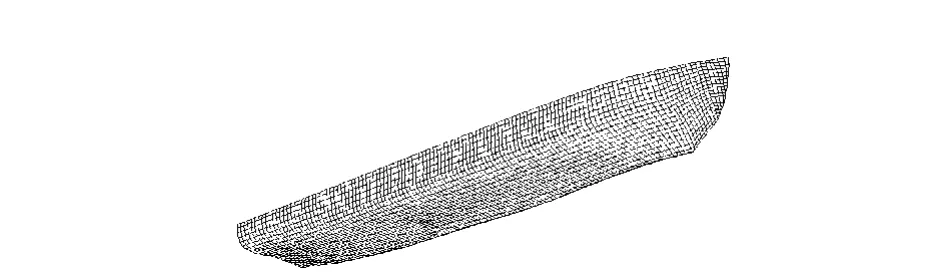
图1 曲面片与控制网格示意Fig.1 Sketch of surface and control mesh

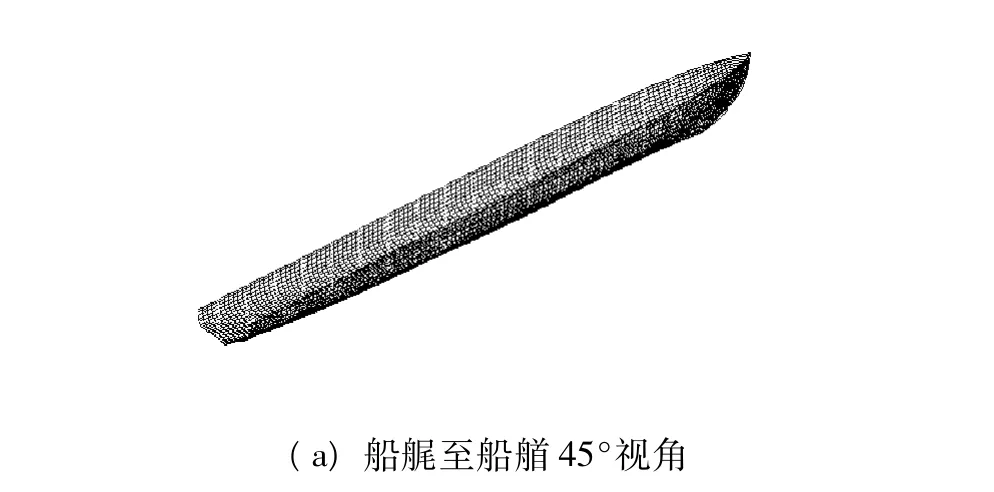
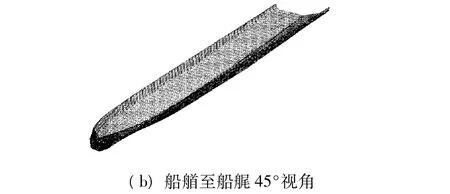
图2 带有折角线的船体曲面图Fig.2 Ship-hull surface with knuckle line

与单体船相比，深V型三体船表面具有一定的特殊性，如通常具有折角线，且有多个船体，涉及二次曲面、自由曲面与平面的组合和尖点处的表达，难点在于对其进行统一表示.因此，对原有的曲线曲面打断，进行局部修改，对曲面次数进行相容性处理［5］，采用升阶、节点插入、删除等技术构造特殊形状.图2为带有折角船体曲面的示例.

1.3 深V型三体船曲面模型

在进行三体船型线设计和曲面造型时，由于型值表提供的母型船型值较单体船复杂，例如同时存在3个船体的横剖面处，某一水线高度处有3个半宽值，应事先对这些型值进行统一处理并按一定顺序排列，以避免在拟合曲线时出现交叉和重复处理.

为便于对3个船体进行同步整体操作，提高拟合速度，考虑以纵向型值参与横剖面的构造的方法，即以水线为基础，先对主体和两个侧体沿纵向统一进行水线加密和拟合，包括对水线、龙骨线、轮廓线的拟合，利用加密后的纵向型值并插入特殊点，在同一纵向位置处形成横剖面型值，并对其加密，拟合出更为精确的横剖线，在两个方向上顺次连接相邻的各插值点，就能生成船体曲面网格.依据以上理论和方法，基于已知主尺度(见表1)和型值，建立某深V型三体船的NUBRS曲面模型，如图3.

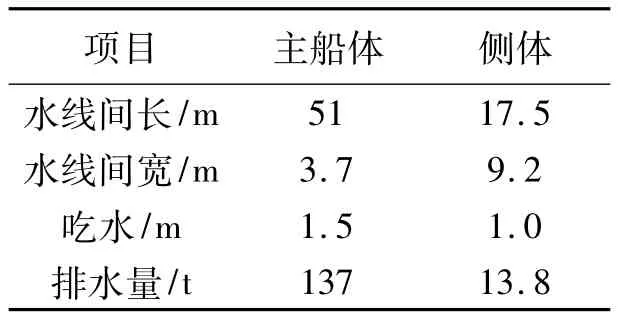
表1 深V型三体船主尺度与排水量Table 1 Principal dimensions of deep-vee trimaran

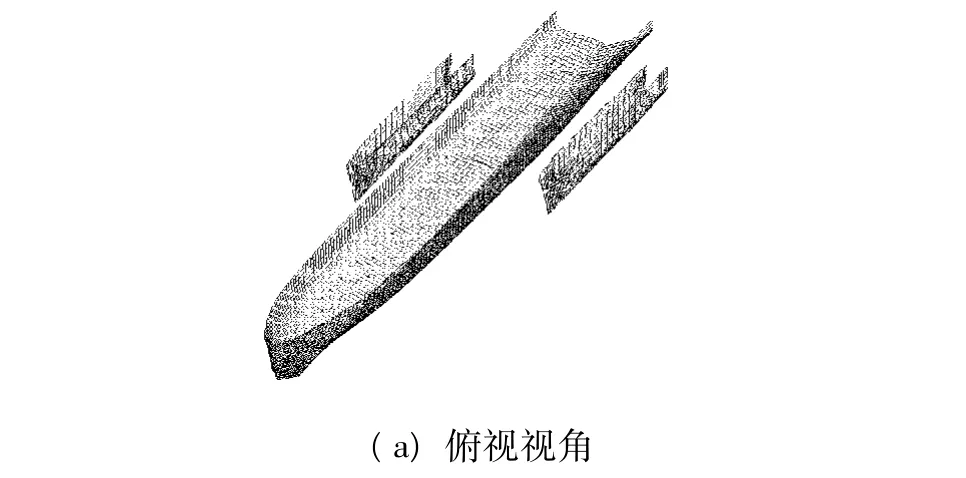
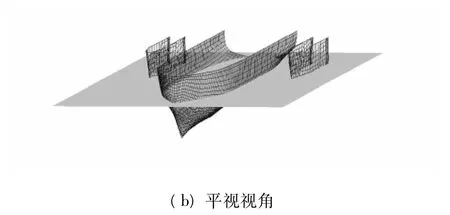
图3 深V型三体船曲面模型实例Fig.3 An example of deep-vee trimaran surface model

1.4 浮态与稳性计算

在建立了深V型三体船的NURBS曲面模型之后，可较为方便地与水面(通常以隐式曲面表示，如图3(b))进行相交计算.本文采用逼近方法中的离散法，对NURBS船体曲面和表示为隐式平面的水面进行相交处理，找出不同船体和甲板与波面的交点，从而得到水线以下的船体形状.具体计算中，应对各个船体与倾斜水面进行求交计算［7］，并根据三体船特点对交点分布进行简化处理，得到倾斜水线下的横剖面形状，从而实现船体在任意浮态下水线面、横剖面、排水体积和重心与浮心位置等相关几何要素的计算.

选择吃水T，横倾角θ，纵倾角ψ作为浮态参数，根据力的平衡条件，建立浮态方程组:

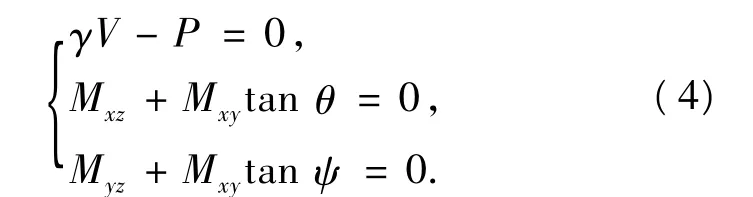
式中:V为排水体积，γ为水的比重，P为重力，Mxz、Myz、Mxy表达式如下:

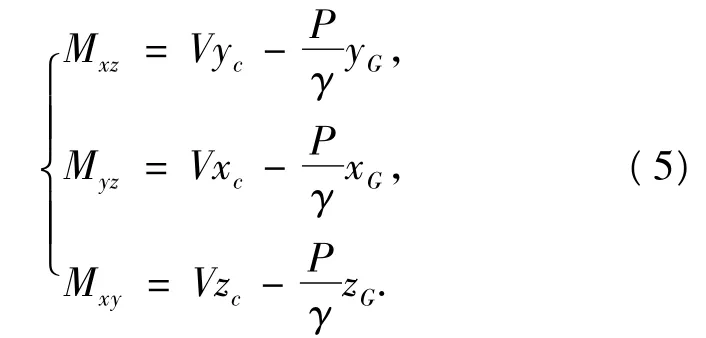
式中:xc、yc、zc为浮心坐标，xG、yG、zG为重心坐标，此时，可利用以几何要素表示的偏导数所组成的jacobi矩阵［8］，求解以浮态参数的修正值为未知数的逐次线性化方程组，得到浮态参数.

在多体船稳性衡准［9］中，主要通过考察静稳性曲线下的各种面积是否符合要求来衡量多体船稳性，因此，本文通过对静稳性曲线进行计算来研究深V型三体船的稳性特点.由上文所述方法，已经得出任意倾斜状态下三体船的浮态，并根据浮态计算相应的静稳性臂GZ值，即在该浮态时重力作用线与浮力作用线之间的距离.根据空间倾斜的几何关系，静稳性臂可表示为以下形式:

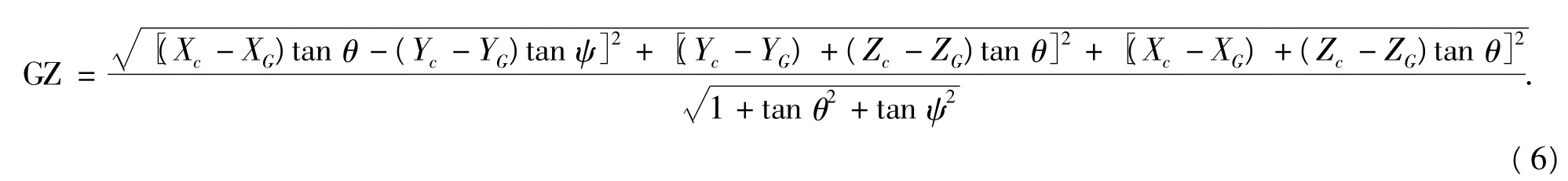
在由上式计算对应一定横倾角的静稳性臂后，进而可以得到该浮态下三体船的稳性曲线.

2 算例分析

2.1 等排水量不同船型的稳性性能比较

为比较深V型三体船与常规圆舭型三体船的稳性性能差异，该文也建立了一同主尺度同排水量的圆舭型三体船，横剖面形状如图4所示.

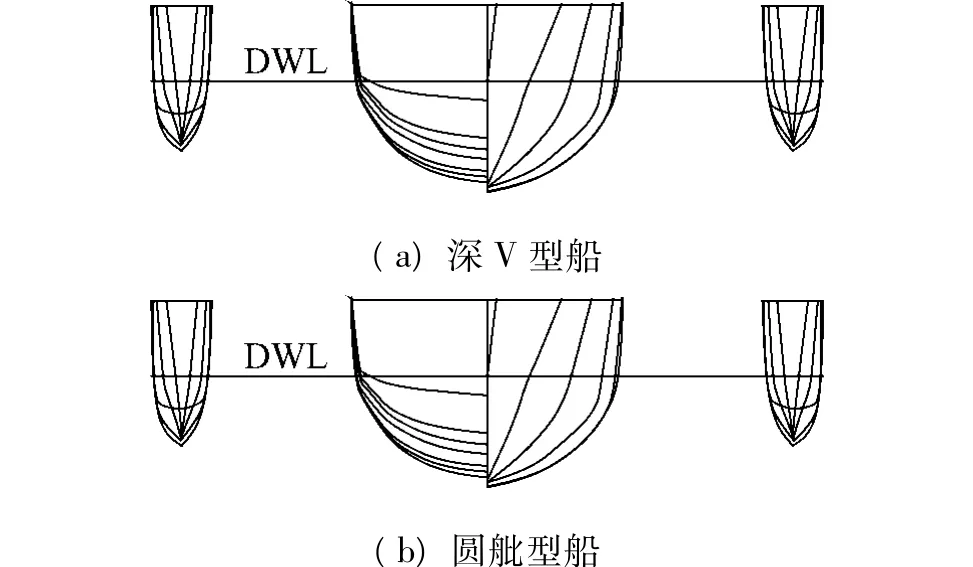
图4 深V型船与圆舭型船横剖面形状Fig.4 Transversal section of deep-vee and round-bilge trimaran

为验证该文方法及所编制程序的正确性，该文同时也采用文献［10］提供的传统稳性计算方法对所建立的圆舭型三体船的稳性进行了计算，图5为这2种方法的比较结果及同排水量深V型、圆舭型2种三体船型静稳性曲线的计算结果.

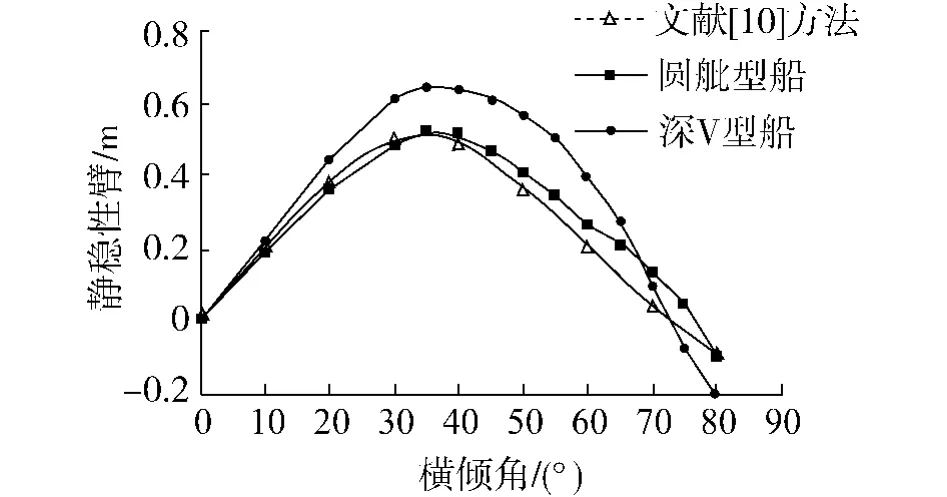
图5 2种三体船型稳性的比较Fig.5 Intact stability of two kinds of trimaran hulls

从图5可以看出，对于圆舭型三体船，该文方法计算结果同采用文献［10］提供的传统方法计算所得结果基本吻合，证明了该程序的正确性.此外，在同排水量的情况下，深V型三体船的最大静稳性臂GZ明显大于圆舭型三体船，且静稳性曲线下的面积大于圆舭型船，表现出更加优异的稳性性能，这是由于深V型船的水线面面积及底升角较大，横倾时浮心横向移动距离大于圆舭型三体船的浮心横向移动距离，从而获得较大的GZ值;但是深V型三体船的稳性消失角较圆舭型船稳性消失角要小，即稳距范围相对较小.

2.2 片体布局对深V型三体船稳性的影响

为了研究片体在不同的横向和纵向位置时对深V型三体船稳性的影响，该文选取了片体在不同的横向位置b(跨距)和纵向位置a的方案，分别计算其稳性来考察片体在不同横向和纵向位置时对稳性的影响.片体与主体位置关系如图6所示.

图6 主船体与片体的相对位置Fig.6 Layout position of main-hull and side-hull

首先研究片体横向位置的不同对三体船稳性的影响，图7是当片体纵向位置a=-10 m时，片体横向位置 b 分别为 3.5、3.7、3.9、4.1 m 时稳性计算结果.

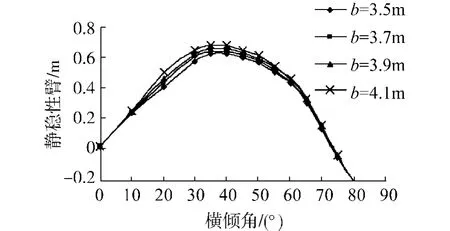
图7 侧体跨距对稳性的影响Fig.7 Influence of side-hull transverse position on stability

从图7的计算结果可以看出，片体跨距b对初稳性影响不大，因为在小角度倾斜时，左右两侧体的排水体积相差不大，其参与构成力矩的作用相当，但在大倾角稳性方面，随着b的增加，三体船最大静稳性臂GZ也越大，可见，在一定范围内适当增加片体与主体的跨距可有效提高三体船的大倾角稳性.

片体横向位置(b=3.7 m)不变，纵向位置a为-0.8、-3.8、-6.8、-9.8 m 时对三体船稳性影响的计算结果见图8所示.

图8表明，片体纵向位置的不同对三体船稳性的影响不大，因此，要想有效提高三体船的稳性性能，并不能通过改变片体的纵向位置来获得.

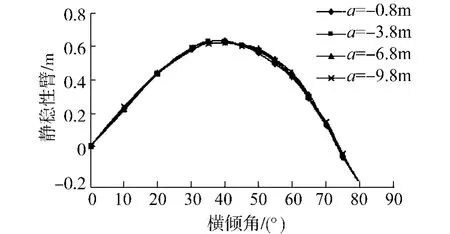
图8 片体纵向位置对稳性的影响Fig.8 Influence of side-hull longitudinal position on stability

2.3 片体吃水的不同对深V型三体船稳性的影响

当片体的吃水 t分别为 1.1、1.0、0.9、0.8 m时，其稳性计算结果如图9所示(此时保持片体的横向位置为3.7 m，纵向位置为-10 m不变).

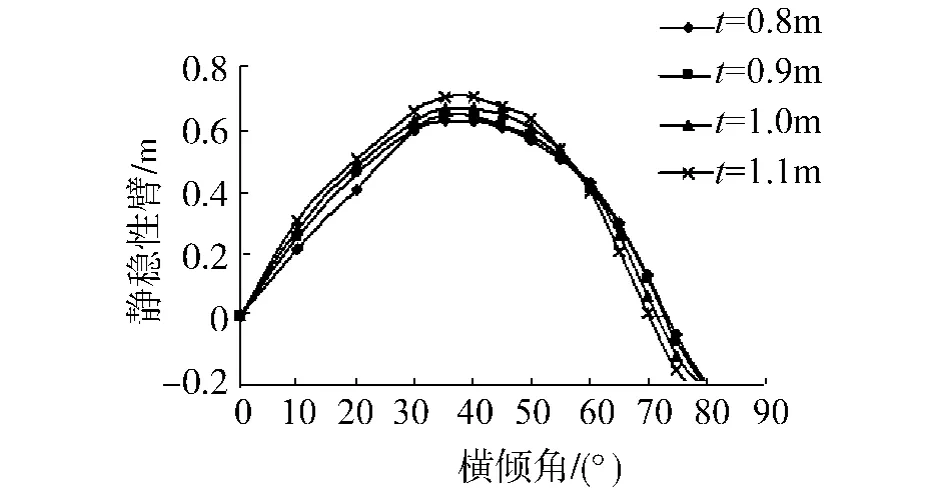
图9 片体吃水对稳性的影响Fig.9 Influence of side-hull draft on stability

从图9的计算结果可以看出，增加片体的吃水，最大静稳性臂GZ随之增大，这是由于随着吃水的增加，片体参与的排水体积比例增大，使得片体对稳性的贡献增加，但在某一角度范围时，几条静稳性臂曲线出现交叉，原因是在超出一定角度后，一侧片体完全入水，而另一侧片体完全出水，因此片体吃水大时的静稳性臂比吃水小时减少迅速，且稳性消失角也比后者小得多.因此，不同的片体吃水情况对三体船的稳性性能也具有较大影响.

2.4 底部横向斜升角对深V型三体船稳性的影响

为研究底部横向斜升角度对深V型三体船稳性的影响，分别选取斜升角为20°、25°、30°时进行计算，结果如图10所示.

从图10的计算结果可以看出，取不同的底部斜升角，静稳性臂变化情况不同，增大深V型三体船斜升角度时，最大静稳性臂GZ随之增加，稳性提高，但是增加到某一角度时，稳性性能反而变差.当斜升角较小如20°时，初稳性较好，但最大静稳性臂偏低，且原点处的斜率即初稳性高GM值较大，摇摆周期短，在风浪中摇摆会比较剧烈;底部斜升角取为25°时，最大静稳性臂值和稳性消失角最大;取30°时，其最大静稳性臂值也偏低，不利于稳性.底部斜升角对稳性的影响主要是由于垂向棱形系数 的改变，使得排水量沿吃水方向的分布产生变化，水线面面积也发生了改变.

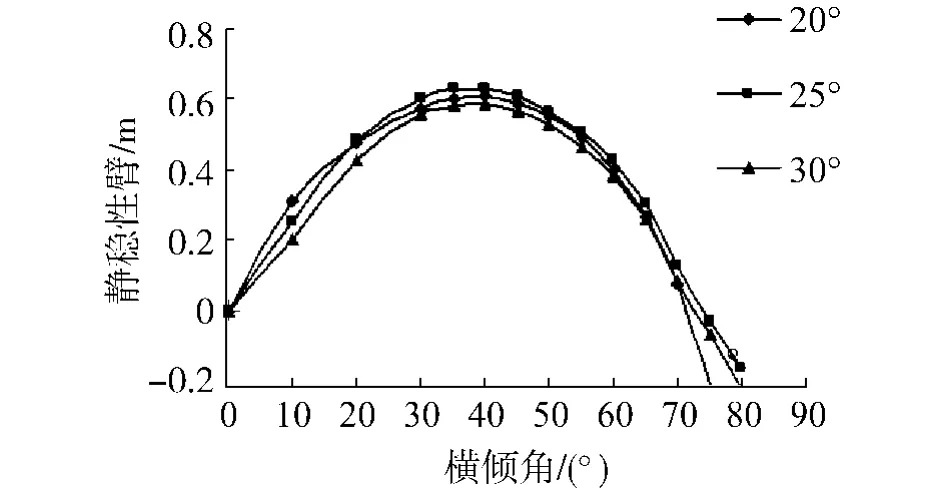
图10 底部横向斜升角对稳性的影响Fig.10 Influence of section oblique angle on stability

3 结论

该文应用NUBRS曲面造型理论，构造一深V型三体船模型，并进行了相应的网格划分，展示了三体船从传统的二维型线图表示向三维立体表示的转化过程，在此基础上进行了深V型三体船稳性计算，并分析了船体形状、片体布局和吃水及底部横向斜升角度对三体船稳性的影响，得出如下结论:

1)不同的船型对三体船稳性有不同的影响，深V型三体船具有比圆舭型三体船更为优异的稳性，因此可以通过适当改变三体船型线获得更好的稳性.

2)片体的位置对深V型三体船稳性的影响主要体现在横向位置上，增大片体跨距可显著提高三体船的大倾角稳性，但纵向位置对稳性影响不大.

3)片体吃水对深V型三体船的初稳性和大倾角稳性都具有较大影响，一般来说，增加侧体吃水可有效提高三体船稳性，但应当注意片体的出入水角度，避免稳性消失角过小，对稳性造成不利影响.

4)底部横向斜升角度对深V型三体船稳性，特别是初稳性高GM产生影响，应选择适当的斜升角以获得适宜的GM值并提高深V型三体船的稳性.

［1］ANDREWS D J，ZHANG J W.Trimaran ships——the configuration for the frigate of the future［J］.Naval Engineers Journal，1995，107(1):77-93.

［2］HENDRIX D，PERCIVAL S，NOBLESSE F.Practical hydrodynamic optimization of a monohull［J］.SNAME Transactions，2001，109(1):173-183.

［3］赵连恩，谢永和.高性能船舶原理与设计［M］.北京:国防工业出版社，2009:51-70.

［4］施法中.计算机辅助几何设计与非均匀有理 B样条［M］.北京:北京航空航天大学出版社，1994:211-254.

［5］林焰，纪卓尚，戴寅生.船体B样条曲面的数学描述及计算机方法［J］.中国造船，1996(4):83-86.LIN Yan，JI Zhuoshang，DAI Yinsheng.Mathematical description and computer method for B-spline hull surface［J］.Shipbuilding of China，1996(4):83-86.

［6］HAZEN G S.FastShip ＆ NURBS modeling:a historical note［J］.Computer-Aided Design，2002，34(7):541-543.

［7］董艳秋，纪凯，黄衍顺.波浪中船舶横摇稳性的研究［J］.船舶力学，1999，3(2):1-6.DONG Yanqiu，JI Kai，HUANG Yanshun.Study on the ship stability in rolling in waves［J］.Journal of Ship Mechanics，1999，3(2):1-6.

［8］赵晓非，林焰.关于解船舶浮态问题的矩阵方法［J］.中国造船，1985(3):55-56.ZHAO Xiaofei，LIN Yan.Matrix method of ship floating problem［J］.Shipbuilding of China，1985(3):55-56.

［9］中国船舶检验局.国际海事组织国际高速船安全规则［S］.北京:人民交通出版社，1995:125-157.

［10］李培勇，裴泳铭，顾敏童，等.三体船完整稳性计算［J］.上海交通大学学报，2002，36(11):1560-1563.LI Peiyong，PEI Yongming，GU Mintong，et al.Intact stability research for multi-hulls［J］.Journal of Shanghai Jiao Tong University，2002，36(11):1560-1563.