无线传感器网络节能型数据融合算法

林蔚，祝启龙

(哈尔滨工程大学理学院，黑龙江哈尔滨150001)

近年来，无线传感器网络的应用范围越来越大，除军事以外，还包括工业、农业、医疗、防疫、科研等各个领域［1］.例如高密度人群细菌监测环境，农业的蔬菜塑料大棚环境监测，森林防火监测、煤矿井下监测，水质量监测等，都是无线传感器网络在不同行业中的应用，无线传感器网络也因此得到迅速发展.然而，网络的稳定性、生命期是网络正常工作的关键.决定网络生命期的主要因素是节点的能量.由于无线传感器网络节点采用易消耗的电池供给，其数据处理和通信能力受到限制，节能对于网络至关重要，也因此成为研究的重点.数据融合能够降低网络数据传输的数量，本文就节能问题提出一种基于数据融合的节能型无线传感器网络.

无线传感器网络数据融合包括数据级融合(低级)，特征级融合(中级)，决策级融合(高级)3个部分.数据级融合在传感器节点处进行，称为下位机融合.特征级融合和决策级融合在基站处进行数据融合，称为上位机融合.数据级融合是最低层融合，即直接对传感器采集的数据进行融合处理，将融合结果向基站或中心节点传输.特征级融合属于中间层融合，一般称作多传感器数据融合.将传感器节点传输的数据进行数据处理，以进行数据校准和状态估计.常见方法有加权平均、卡尔曼滤波、模糊逻辑、神经网络等方法.

由于数据融合技术已成为无线传感器网络节约能源研究的重点，许多学者针对多传感器数据的融合问题进行了研究.文献［2］、［3］采用模糊理论对各传感器测得数据之间的接近程度进行处理，通过接近度矩阵度量各传感器测得数据的综合接近程度，分配数据在融合过程中的权重，得出特性指标.文献［4］、［5］通过讨论分簇的融合方式，分析簇内数据的融合算法误差成因，提出先进行簇内测量修正、再进行簇内数据融合.文献［6］通过传感器的重要度，从各个传感器对模糊命题支持度的一致度，以及传感器重要度对数据融合结果的复合作用等三方面分析，提出一种模糊传感器数据融合.上述数据融合均运行在上位机，底层数据仍采用采集一个数据发送一个数据的方法，这种方法不利于节省节点能源.

1 TFA数据融合算法

本文提出算法TFA(twice fusion algorithm)，其目标是降低节点能量消耗.其工作原理是:首先在网络的数据采集点处，采用阈值限定和均值融合方法，进行下位机(节点)的数据融合;再在上位机(控制中心或网关)进行多传感器数据补偿和融合.通过对节点采集数据的融合，减少节点通信量，从而减少能耗，延长WSN生存时间.虽然计算会增加能耗，然而计算上的能耗与通信消耗的能量相比是10-3倍［7］，并且由于传感器的相对误差小于 0.01［8-9］，当设定合适的参数和阈值时，不影响融合结果.因此，节能方面的优势可以得到充分体现.

图1 传感器数据融合结构图Fig.1 Wireless sensor network data fusion chart

TFA数据融合模型如图1所示.它包含了传感器网络从数据采集到上位机融合的全过程.其中包括:1)传感器节点采集数据后的数据融合，2)上位机数据补偿，3)上位机数据融合.

1.1 下位机(节点)数据处理

每个传感器节点采集数据，形成各自的列矩阵.其中，每列表示同一传感器每过一个φ时刻测得的数据.K个传感器产生k列数据，形成一个矩阵.

由于节点在相邻时间测得的数据相似，本文将相似数据融合，去除冗余.

假设无线传感器网络:

1)由k个传感器节点监测同一环境.

2)每个传感器以等时间间隔 采集数据:aij，(i=1，2，3，…;j=1，2，3，…).

采集后从同一时刻开始计算.则测得的数据用矩阵表示为A:

其中，每一列数据都存储在本地节点内存中，它是同一个传感器在不同φ时刻测量值.每行表示同一时刻不同传感器采集的数据，显然，由于传感器测得的数据在相邻的时间上具有相似性，节点的相邻数据具有相似性.为了节省节点能量，同时由于在底层观测值的不稳定性以及不确定性，对每列数据进行均值融合方法，并发送这个均值给控制中心(上位机).均值计算的过程如下:

设定2个阈值δ和τ.其中δ限定了数据最大距离，δ取传感器的最大误差.τ是限定采集次数，由于节点每隔时间采集一次数据，设定阈值τ是为了避免传感器发送时间间隔过长.每个传感器将采集的数据保存在节点存储器中，直到当这些数据之间的任意两个差值超过阈值δ，或采集次数超过τ时，以本次采集的数据次数为第i次，对已采集的前i-1次的数据进行均值计算，然后发送到控制中心.发送条件:1)当第i个采集的数据与之前的i-1个数据中的某个差值过大，数据出现突变趋势，为保持数据的一致性，TFA算法对前i-1次的数据进行均值计算;2)当采集数据的次数达到τ次时，为了与1)中的i取得一致，TFA算法同样取第i-1次之前的进行均值计算，将第i次的数据作为下一次采集的第一个数据，由此得到节点数据融合算法如下:

1)设a1j为节点j采集的第1个数据;

2)每采集一次数据aij，分别与前i-1次的数据a1j，a2j，…，ai-1j进行比较，即:|aij-akj|，(k=1，2，…，i-1).

①当其中的任一数据距离超过阈值δ时，即

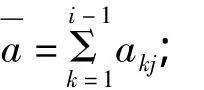
3)将第i次采集的数据aij作为下一次采集的第一个数据a1j;

5)重复1)～4).

1.2 上位机数据补偿

由于数据在下位机进行了融合，使数据存在一定的失真，在上位机应尽可能给予补偿.补偿原则是:在每行补偿该节点在φ时刻的均值.上位机数据仍是一个矩阵.其行是φ时刻，列是每个传感器在φ时刻的均值.算法是:当上位机接收到某传感器的一个均值，在为(这个)传感器预留的存储空间(矩阵B中)补偿传感器的均值，方法是:补偿上位机接收时刻的前一时刻(以φ为单位)以及之前各时刻未补偿的值，这些补偿的时刻，即为矩阵B中元素的行标，传感器号为列标.即每过一个φ时间，就应该产生一行数据，一行中每个数据值以传感器在该时刻的平均值作为该位置的补偿数据值，这就形成了数据补偿矩阵B:

其中，bij表示第i个φ时刻第j个传感器的数据补偿值，bij的取值满足:

其中，|ak'1-ak1|＜ δ，k、k'=1，2，3，k≠k';i≤τ.

1.3 上位机数据融合

在上位机对矩阵A进行数据补偿和时间上的统一后，得到数据补偿矩阵B.当上位机接收完每个传感器同一时刻的数据，即得到矩阵B的一行，为了得到这一时刻的数据，算法TFA对某一行数据进行多传感器数据融合，这一行数据来自于不同传感器.融合方法是对期望真值进行拟合，每一时刻(即每一行)融合为一个数据，它代表这一时刻的监测值，本文采用加权平均的方法对矩阵B中的每行数据进行拟合.算法如下:

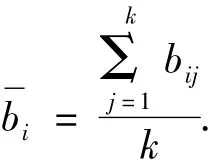
1.3.2 权重及融合值计算

因为距离越大，偏离均值越远，故权值取均值距离的倒数.

则融合值Ci(第i行的融合值):

2 仿真实验与分析

仿真环境采用C51RF-3-PK的软件仿真系统，同时为了进行算法比较，底层数据算法TFA采用文献［10］的原始数据，对其进行数据融合.设参数值为:τ=5，δ=5.

表1是文献［10］的原始数据，是3个传感器在算法TFA对表1中数据进行融合处理.

首先进行节点数据融合，得到融合矩阵A，再发送给上位机，得到数据补偿矩阵B，如表2所示.

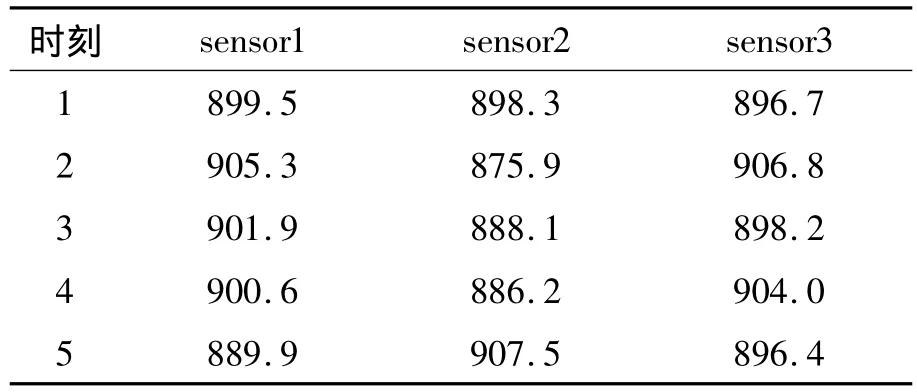
表1 传感器测量值Table 1 Measured value ℃

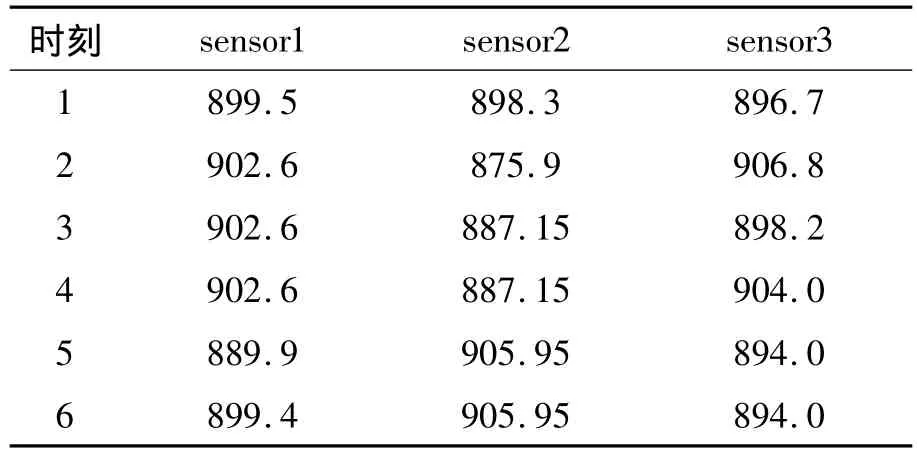
表2 数据补偿值Table 2 Compensation for the value of data ℃

表3是算法TFA在上位机的融合值以及相对误差和绝对误差.

表3 下位机数据融合值Table 3 Lower machine data fusion value

表4给出算法TFA、主成分分析方法PCA(principal component analysis)、平均值方法AA(averaging algrithm)以及可靠性分析方法RA(reliability analysis)等，针对同一原始采集数据进行不同融合算法后的结果比较.

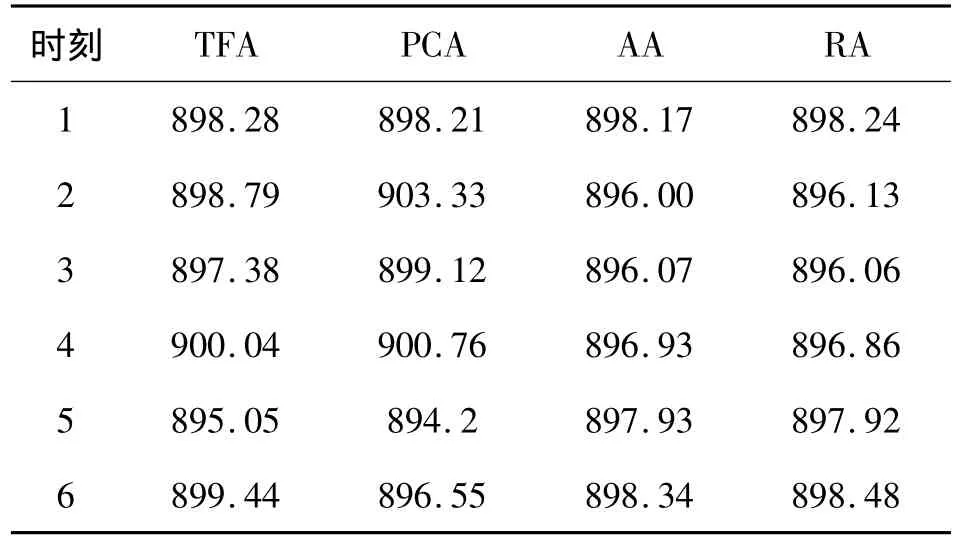
表4 各种方法的融合结果Table 4 The results of various methods of fusion (°)

图2给出误差分析.从图2的误差分析图可以看出，算法TFA更接近于真值(900℃)，说明算法TFA比其他算法更合理.

图2 不同方法的绝对误差分析图Fig.2 The absolute error analysis chart

为了说明算法TFA在能量节约上的效果，用TFA算法与未经过传感器节点融合，而是直接将采集的数据发送给上位机的算法所消耗的能量进行比较，得到表5.仿真结果表明，随着阈值δ的增加，节点节约较多的能量;但随着δ值的增加，融合结果的精度会降低，再加上节点存储能力有限，因此，阈值不能无限增大;反之，随着阈值减小，能量消耗多，但精度会提高.当取适当的阈值时，算法TFA的绝对误差较小，可以保证数据的精确性和稳定性，而且节省能源消耗的绝对误差较小.

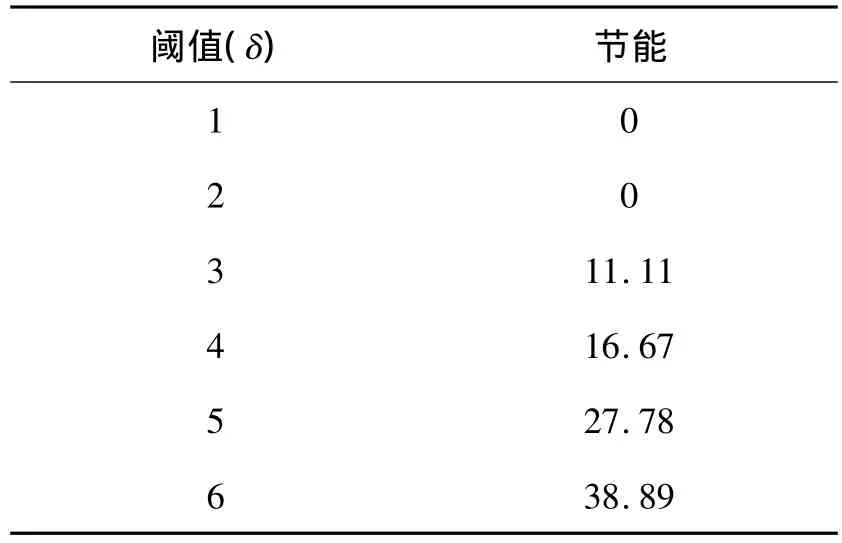
表5 不同δ参数值节约能源的百分率Table 5 δ values for different parameters of the node＇s energy savings %

3 结束语

由于传感器节点数量的冗余性、分布的随机性以及相邻传感器对同一目标区域监测数据具有相似性，使得无限传感器网络的监测数据具有冗余性;又因为传感器节点在能源、存储空间和计算能力的局限性，因而过多地传送冗余数据将消耗过多的能量，将缩短WSN的生存期.为减轻上述客观因素对网络生命期的影响，有必要将数据进行融合.本文提出的二次融合算法TFA，首先在各个节点采集数据的过程中，对数据进行底层的数据融合，以减少冗余信息的传输量，节省监测网络的能量;其次算法TFA利用监测值在时间和空间上相似的特点，在上位机(控制中心)以多传感器数据融合方式，对数据进行补偿和融合，进而得到某一段时间对监测环境的监测结果.仿真结果表明，TFA算法在节能方面以及数据精度方面都取得较好的结果.此外，本文没有考虑无线传感器网络的多跳路由情况，有待于进一步讨论.

［1］王志宇，车承钧，王阳.基于物联网的区域农田土壤墒情监测系统研究［J］.自动化技术与应用，2010，28(12):39-42.

WANG Zhiyu，CHE Cheng jun，WANG Yang.Research of self-congnitive internet of things model and its applications［J］.Techniques of Automation＆Applications，2010，28(12):39-42.

［2］焦竹青，熊伟丽，张林，等.基于信任度的多传感器数据融合及其应用［J］.东南大学学报自然科学版，2008，38(A01):253-257.

JIAO Zhuqing，XIONG Weili，ZHANG Lin，et al.Multi-sensor data fusion method based on belief degree and its applications［J］.Journal of Southeast University:Natural Science Edition，2008，38(A01):253-257.

［3］LEE M F R，STANLEY K，WU Q M J.Implementation of sensor selection and fusion using fuzzy logic［C］//IFSA World Congress and 20th NAFIPS International Conference.Vancouver，BC:2001，328-333.

［4］MARTALO M，FERRARI G.A simple information-theoretic analysis of clustered sensor networks with decentralized detection［J］.IEEE Communications Letters，2010，14(6):560-562.

［5］翟建设，李娜，吴青.基于分簇的无线传感器网络簇内数据融合算法［J］.计算机工程，2008，34(11):134-136.

ZHAI Jianshe，LI Na，WU Qing.Improved algorithm of clustering-based data fusion for WSN［J］.Computer Engineering，2008，34(11):134-136.

［6］马琦，张记龙，王志斌.无线传感器网络簇内自适应融合算法研究［J］.计算机应用研究，2009，7(26):2502-2503，2507 .

MA Qi，ZHANG Jilong，WANG Zhibin.Study of adaptive data fusion algorithm within clusters for WSN［J］.Application Research of Computers，2009，7(26):2502-2503，2507.

［7］张强，杨涛.用于环境监测的自供电传感器网络［J］.仪表技术与传感器，2008，2:34-36.

ZHANG Qiang，YANG Tao.Self-powered wireless sensor network for environment monitoring［J］.Instrument technique and sensor，2008，2:34-36.

［8］齐志才，马占敖，江萍.提高带隙温度传感器精度方法的研究［J］.仪表技术与传感器，2004，7:46-47.

QI Zhicai，MA Zhanao，JIANG Ping.Study of method improving accuracy of band-gap temperature sensor［J］.Instrument Technique and Sensor，2004，7:46-47.

［9］杨雪芳，蔡萍，杨重远.提高容栅位移传感器精度的有效方法［J］.传感器技术，2005，24(9):32-34 .

YANG Xuefang，CAI Ping，YANG Chongyuan.Effective ways to improve accuracy of capacitive grating displacement sensor［J］.Journal of Transducer Technology，2005，24(9):32-34.

［10］董九英.多传感器数据融合的主成分方法研究［J］.计算机工程与应用，2009，45(33):111-113.

DONG Jiuying.Study on principle component method for multi-sensor data fusion［J］.Computer Engineering and Applications，2009，45(33):111-113.