B-半（E，F）-凸半无限规划的对偶性及鞍点理论

刘婷婷，张庆祥，高 颖，张永战

（延安大学数学与计算机科学学院，陕西延安 716000）

B-半（E，F）-凸半无限规划的对偶性及鞍点理论

刘婷婷，张庆祥，高 颖，张永战

（延安大学数学与计算机科学学院，陕西延安 716000）

利用B-半（E，F）-凸函数的有关性质讨论了B-半-（E，F）-凸半无限规划的几个对偶定理及鞍点理论。

B-半（E，F）-凸函数；半无限规划；对偶理论；鞍点理论

定义1［1］称集合M⊂Rn为（E，F）-凸的，若存在两映射E，F：Rn→Rn，使对任意x，y∈M和λ∈［0，1］，有λE（x）+（1-λ）F（y）∈M。

定义2［2］称f：M→R为半（E，F）-凸函数，若存在两映射E，F：Rn→Rn，使对任意x，y∈M和λ∈［0，1］，有f［λE（x）+（1-λ）F（y）］≤λf（x）+（1-λ）f（y）。

定义3［3］称f：M→R为B-半（E，F）-凸函数，若存在两映射E，F：Rn→Rn，使M为（E，F）-凸集，实值函数b（x，y，λ）≥0，使

性质1若f是局部Lipschitz函数，且f是B-半（E，F）-凸的，则

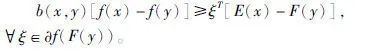
1 对偶理论

以下均假设任意的x∈M，有E（x）∈M，F（x）∈M。考虑半无限规划（P）：

min f（x），

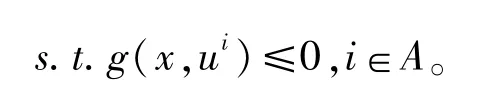
其中A=｛i：g（x，ui）≤0，u∈Y⊂Rn｝，Y为无限可数集。

假设 （1）存在一个乘子集｛λi：i∈A，i≥0，并且只有有限多个λi≠0｝。任意的有x0∈M以下条件成立：（2）（P）的Lagrange对偶规划（D）：

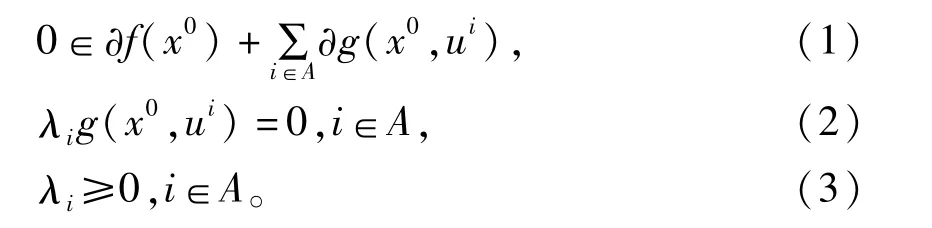
（2）（P）的Lagrange对偶规划（Ｄ）：

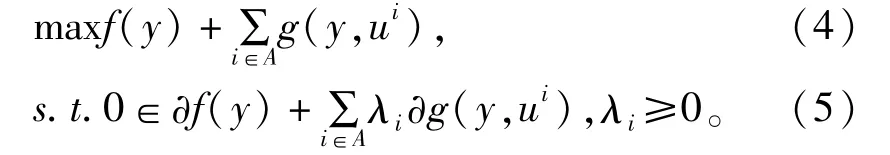
对于一切i∈A，仅有有限个λi≠0。

定理1设f（x），g（x，ui）（i∈A）对于任意的ui∈Y关于点y是B-半（E，F）-凸函数，若x和y分别是（P）和（D）的可行解，且有y∈F（y），则

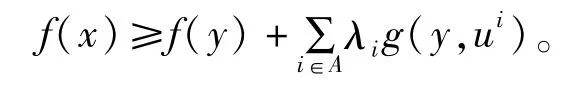
证明因为f（x），g（x，ui）（i∈A）关于点y是B -半（E，F）-凸的，所以

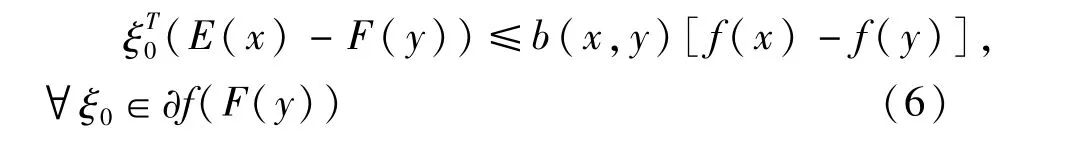
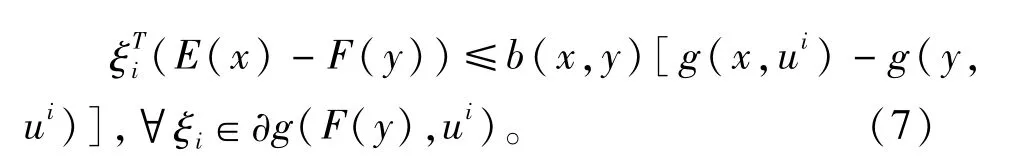
给（7）式乘以λi≥0，并求和，得

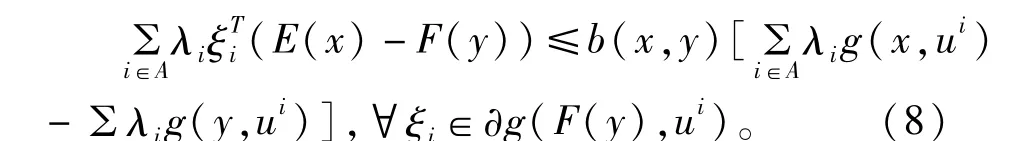
利用假设及（6），（8），（9），得

因为x∈M，g（x，ui）≤0，b（x，y）≥0，-b（x，y）i∑∈Aλig（x，ui）≥0，b（x，y）［f（x）-f（y）-i∑∈Aλig（y，ui）］≥0，所以f（x）≥f（y）+i∑∈Aλig（y，ui）。

定理2设f（x），g（x，ui）（i∈A）对于任意的ui∈Y关于点x0是B-半（E，F）-凸函数，y∈F（y），若x0是（P）的最优解，（x0，ui，λ）为（D）的可行解，且i∑∈Aλig（x0，ui）=0，则（x0，ui，λ）为（D）的最优解。

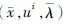
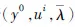
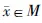
2 鞍点理论

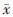
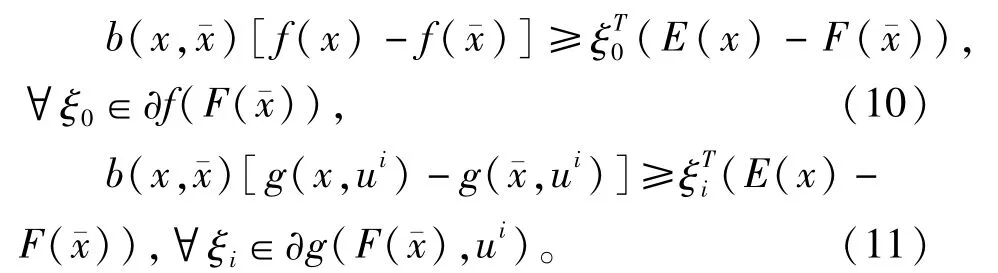
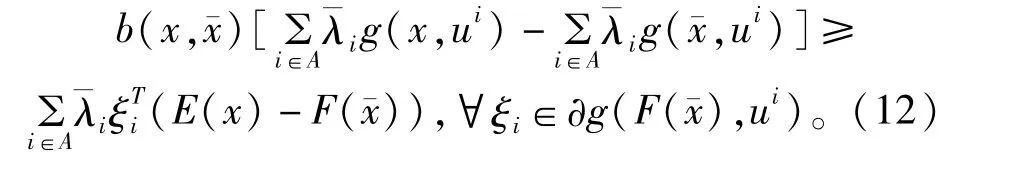
结合（10），（11）和（13），有

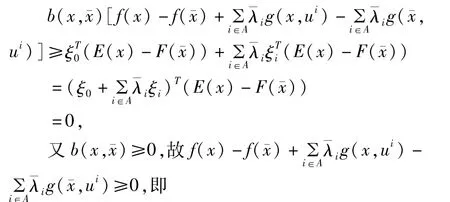
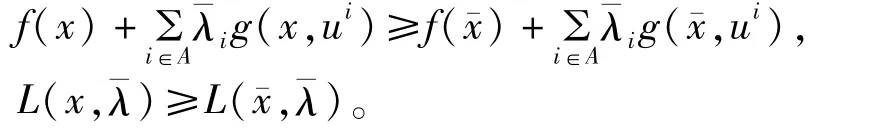
证明结合定理4和定理5可知。

［1］Jian J.B.，On（E，F）-Generalized Convexity［J］.International Journal of Mathematical Sciences，2003，2（1）：121-132.

［2］胡清洁，梁远信，简金宝.一类新的广义凸函数及相应凸规划的最优性条件与对偶［M］.香港：Globle-Link出版社，2004：65-71.

［3］曾友芳，简金宝，晁绵涛.B-半（E，F）-凸函数和规划［J］.运筹学学报，2009，13（2）：68-82.

［4］S.K.Mishra.Onmultiple-objective optimization with generalized univexity［J］.J.Math.Anal.Appl.1998，224：131-148.

［4］张蕾蕾，张庆祥.一类Eb，ρ-凸半无限规划的对偶性及鞍点理论.西安邮电学报，2006，11（3）：123-127.

［责任编辑 贺小林］

Duality and Sadd le-Point Theory for B-Sem i-（E，F）-Convex Sem i-Infinite Programm ing

LIU Ting-ting，ZHANG Qing-xiang，GAO YING，ZHANG Yong-zhan
（College of Mathematics and Computer Science，Yan an University，Yan an 716000，China）

In this paper，the duality and saddle-point theory of semi-infinite programming for B-semi-（E，F）-convex functions are discussed by using properties of B-semi-（E，F）-convex functions.

B-semi-（E，F）-convex function；semi-infinite programming；duality theorem；saddle-point theorem

O221.2

A 文章编号：1004-602X（2011）04-0012-03

20111008

刘婷婷（1987—），女，陕西绥德人，延安大学在读硕士研究生。