弱积分C-半群拓扑
董晓丽,赵华新
(延安大学数学与计算机科学学院,陕西延安 716000)
弱积分C-半群拓扑
董晓丽,赵华新
(延安大学数学与计算机科学学院,陕西延安 716000)
利用积分C-半群及连续线性泛函的概念,引入了一个新的局部凸向量拓扑,并对其基本性质及积分C-半群在新的局部凸线性拓扑意义下的性质进行了初步研究。
积分C-半群;局部凸向量拓扑;生成元;弱积分C-半群拓扑
1 预备知识
定义1.1设(X,‖·‖)是一个Banach空间,(X,‖·‖)′为X的共轭空间,B(X)为X到X的有界线性算子的全体构成的算子空间,n∈N+,C∈B(X),B(X)中的一个强连续算子族{T(t):t≥0}称为(X,‖·‖)上的一个n次积分C-半群,即满足下列条件:
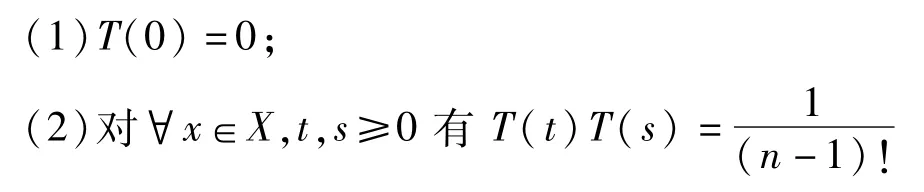
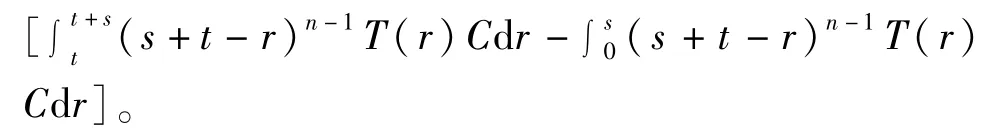
又称{T(t):t≥0}是非退化的,如果
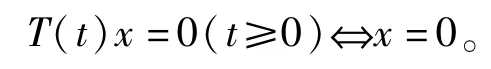
定义1.2n次积分C-半群{T(t):t≥0}的无穷小生成元A是如下定义的算子:

定义1.3A的C-预解式定义如下:
PC(A)={λ:λ-A为单射且R(C)⊂R(λ-A)}。对∀λ>ω,及x′∈(X,‖·‖)′,令
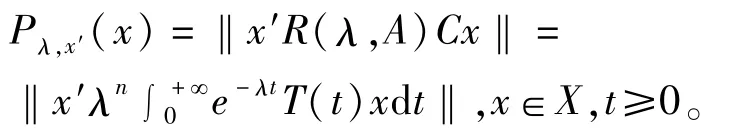
则利用积分C-半群的定义容易验证,对∀x,y∈X及λ>ω有:
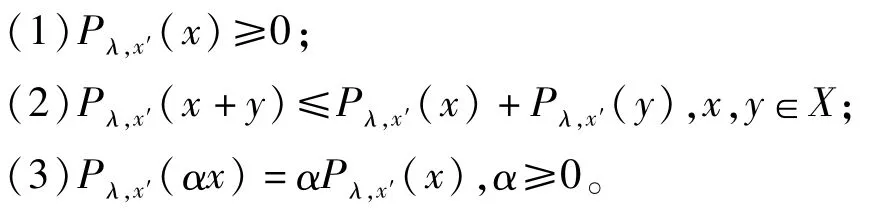
即Pλ,x′(x)是X上的一个半范数,从而由半范数族S={Pλ,x′:λ>ω}可以确定一局部凸向量拓扑,记为τ*。
2 主要结果
定义2.1由上述半范数族S={Pλ,x′:λ>ω}所确定的X上的局部凸向量拓扑,称为X上的相应于x′的弱积分C-半群拓扑,相应的局部凸线性拓扑空间记为(X,τ*)。
引理2.1[5]设E是线性空间,A,B是E上的两族半范数,则由A确定的拓扑弱于由确B定的拓扑的充要条件是:对每个q∈A,必存在p1,p2,…,pm∈B以及正数c1,c2,…,cm,使得对一切x∈E成立:
q(x)≤c1p1(x)+c2p2(x)+…+cmpm(x)。
定理2.1X上的弱积分C-半群拓扑弱于积分C-半群拓扑,也弱于由范数所确定的局部凸向量拓扑。
证明因为对∀λ>ω及x′∈X′,x∈X有
Pλ,x′(x)=‖x′R(λ,A)Cx‖≤‖x′‖·‖R(λ,A)Cx‖≤‖x′‖·‖R(λ,A)C‖·‖x‖,由此及引理2.1与积分C-半群拓扑的概念,易见命题成立。
定义2.2在一个局部凸线性拓扑空间X中,若对任意Cauchy序列{xn},{x′R(λ,A)Cxn}(λ>ω)都收敛,则称X关于相应于x′的弱积分C-半群是完备的。
定理2.2局部凸线性拓扑空间(X,τ*)是弱积分C-半群完备的。
证明设{xn}是(X,τ*)的任意Cauchy序列,则对于任意连续半范数q(x)及ε>0,集合U=
{x:q(x)<ε}构成0的一个邻域,从而必存在自然数N,使得当n,m>N时,有
(xn-xm)∈U,即q(xn-xm)<ε。
特别地,对任意Pλ,x′(x)∈S有
Pλ,x′(xn-xm)=‖x′R(λ,A)C(xn-xm)‖
=‖x′λn∫0+∞e-λtT(t)(xn-xm)dt‖
=‖x′λn∫0+∞e-λtT(t)xndt-x′λn∫0+∞e-λtT(t)xmdt‖<ε。
可知{x′R(λ,A)Cxn}(λ>ω)为Banach空间(X,‖·‖)中的Cauchy序列,从而{x′R(λ,A)Cxn}(λ>ω)必收敛,由定义2.2得证。
定理2.3当{T(t):t≥0}是非退化的积分C-半群且x′≠0时,弱积分C-半群拓扑τ*是分离的。
证明由于{T(t):t≥0}是非退化的,即如果对∀t有T(t)x=0,必有x=0。所以对∀x≠0有sαu>pωPα,x′(x)=sαu>pω‖x′R(α,A)Cx‖>0。从而对∀x≠y,即x-y≠0,必存在一α∈(ω,+∞),使得
Pα,x′(x-y)=3d>0,令V={x:Pα,x′(x)≤1},则x的邻域x+dV与y的邻域y+dV彼此分离,即半群拓扑τ*是分离的。
由于Pλ,x′(x)=‖x′R(λ,A)Cx‖≤‖x′‖·‖R(λ,A)C‖·‖x‖,所以拓扑τ*弱于由范数所确定的局部凸向量拓扑,从而当{T(t):t≥0}是(X,‖·‖)上的积分C-半群时,它也是局部凸线性拓扑空间(X,τ*)上的积分C-半群。
关于相应由不同的x′∈X′的弱积分C-半群拓扑之间的关系,有如下结果:
定理2.4设x1′,x2′∈X′,x′=αx1′+βx2′,其中α,β为任意常数,即x′是x1′,x2′的任意线性组合,则由半范数族{Pλ,x′(x)}所确定的局部凸向量拓扑弱于由半范数族{Pλ,x1′(x),Pλ,x2′(x)}所确定的局部凸向量拓扑。
证明因为对∀x∈X,有
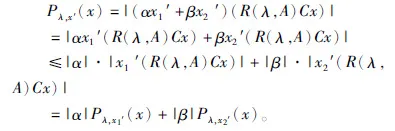
再利用引理2.1,可证得本定理结论。
[1]赵华新.C0-半群拓扑(I)[J].纯粹数学与应用数学,2006(3):420-423.
[2]赵华新.C-半群拓扑[J].河南科学,2006(2):157-158.
[3]王晓梦,赵华新,常胜伟.积分C-半群拓扑[J].延安大学学报(自然科学版),2008,27(2):5-6.
[4]常胜伟,赵华新.弱C-半群拓扑[J].江西科学,2007,25(6):669-671.
[5]夏道行,杨亚立.线性拓扑空间引论[M].上海:上海科学技术出版社,1986.
[6]刘曼,郭玲利.n次积分C-半群的表示定理[J].徐州工程学院学报,2005(5):4-8.
[责任编辑 贺小林]
Weakly Integrated C-Sem igroup Topological
DONG Xiao-li,ZHAO Hua-xin
(College of Mathematics and Computer Science,Yan an 716000,China)
By using the integrated C-semigroup of bounded linear operator and continuous linear functional,a new locally convex vector topological is introduced,some propositions of it are given.
integrated C-semigroup;locally convex vector topological;generator;weakly integrated C-semigroup topological
O177.2
A
1004-602X(2011)04-0004-02
20110920
董晓丽(1986—),女,陕西铜川人,延安大学在读硕士研究生。

