Banach空间上强混合的广义C0-半群

高 峰，赵华新

（延安大学数学与计算机学院，陕西延安 716000）

Banach空间上强混合的广义C0-半群

高 峰，赵华新

（延安大学数学与计算机学院，陕西延安 716000）

在传统强混合C0-半群的基础上，给出了广义强混合C0-半群的定义，并且利用广义C0-半群的生成元的一些性质，证明了每个可分无限维复Banach空间上都存在一个强混合的广义C0-半群。

强混合；广义C0-半群；Banach空间

文献［1］在C0-半群的基础上，将其定义中的T（t），t≥0是强连续算子族减弱为CT（t）是强连续算子族，其中C∈B（X），引入了广义C0-半群的概念。文［2］证明了每个可分无限维复Banach空间上都存在一个强混合的C0-半群。本文在文献［1］和［2］的基础上给出了广义强混合C0-半群的概念并且证明了每个可分无限维复Banach空间上都存在一个强混合的广义C0-半群。

1 预备知识

定义1.1［1］｛T（t），t≥0｝是Banach空间X中的单参数有界线性算子族，C∈B（X），其中B（X）为X到X的有界线性算子族全体，若满足以下条件：

（1）T（0）=I，I是X上的单位算子；

（2）T（t+s）=T（t）T（s），t≥0，s≥0；

（3）CT（t）是强连续算子，t≥0。

则称｛T（t），t≥0｝是X上的广义C0-半群。

定义1.2［1］线性算子A是广义C0-半群｛T（t），t≥0｝的无穷小生成元，是指：

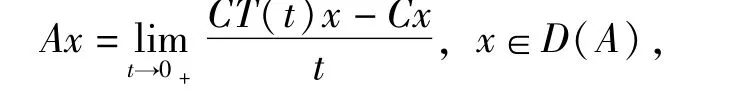
定义1.3［2］称一个C0-半群｛T（t），t≥0｝是强混合的，如果对X的任意两个非空开集U，V，存在某个L∈R+，使得对任意t≥L都有T（t）U∩V≠Φ。

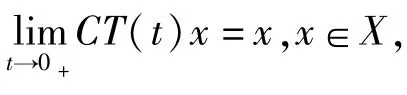
（1）∀x∈X，Lλx∈D（A），（λC-A）Lλx=C2x；

（2）若x∈D（A），Lλ（λC-A）x=C2x。

引理1.2［1］（生成定理）设X为Banach空间，C∈B（X），A为线性算子，且满足：

（1）A：D（A）⊂X→X闭稠定；

（2）x∈D（A），ACx=CAx；

则A是广义C0-半群T（t）的生成元，（λCA）-1C2x=C2（λC-A）-1x=Lλx，x∈X。

引理1.3［3］设X是一个可分无限维Banach空间，则存在序列（ep）p∈N⊂X和（φq）q∈N⊂X*，满足如下的条件：

2 主要结果

下面是本文中的主要定理。

定理2.1设X是一个可分无限维的Banach空间，则由A生成的广义C0-半群｛T（t）：t≥0｝在X上是强混合的。

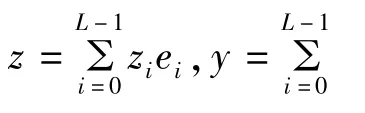
由引理1.2知，由A生成的广义C0-半群

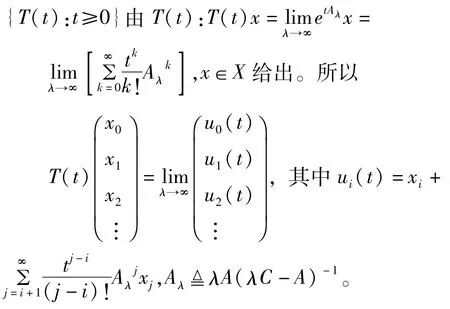
从某个t开始，定义向量如下：

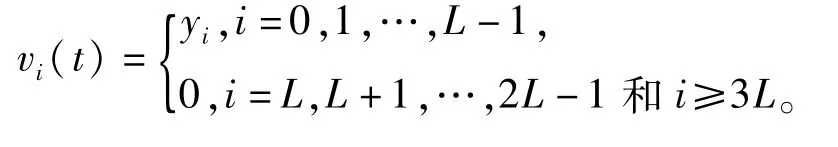
设ui（t）=zi，i=0，1，…，L-1，这里

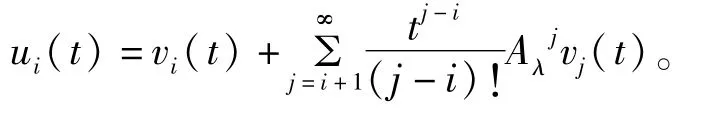
则系数v2L+1（t），…，v3L（t）是下面线性方程组的解：

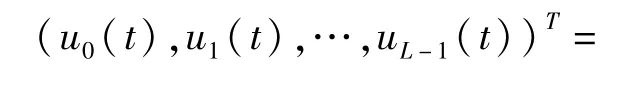
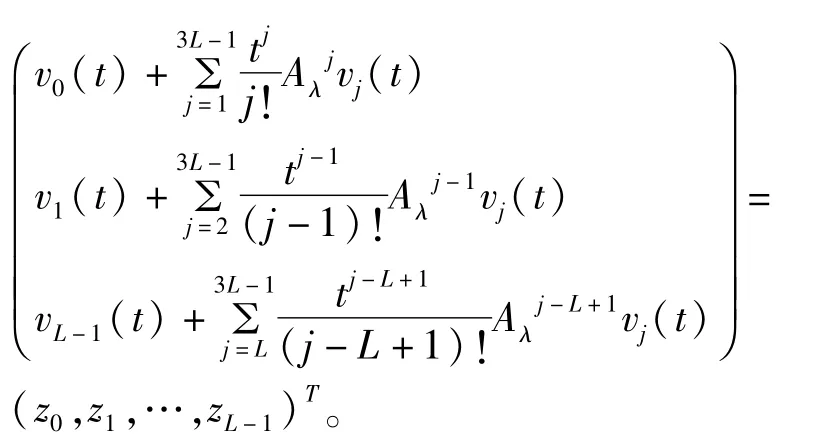
由这个线性方程组可知

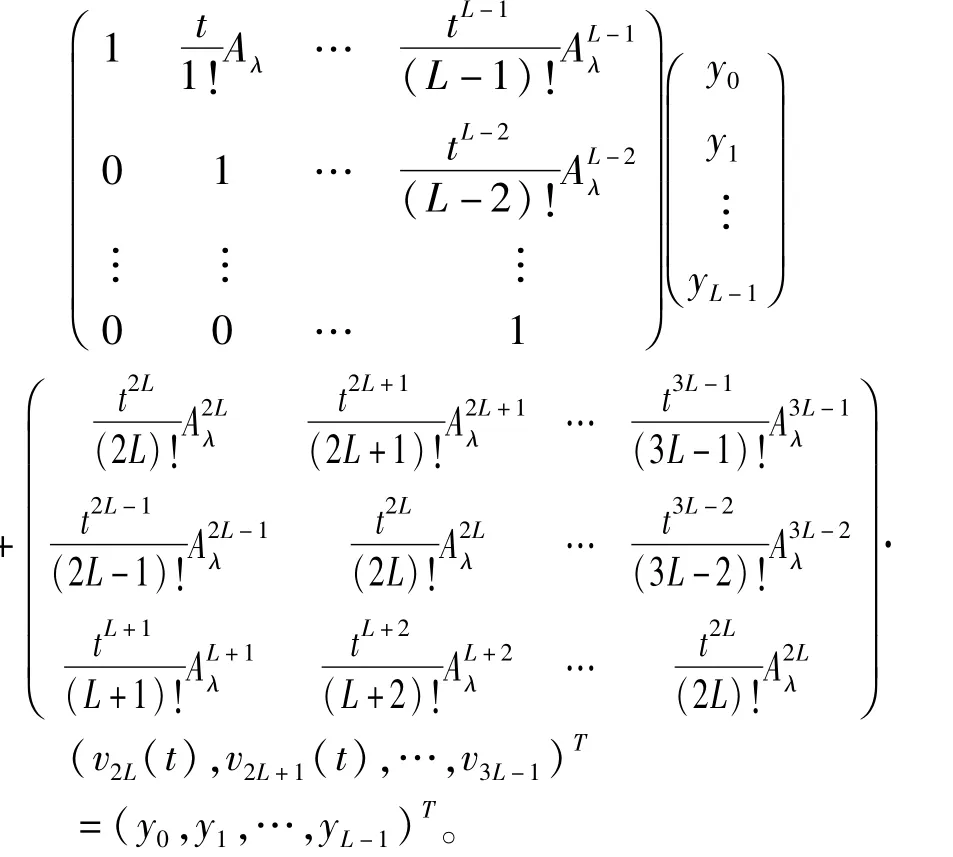
注意到v2L（t），v2L+1（t），…，v3L-1（t）的系数矩阵可以写作

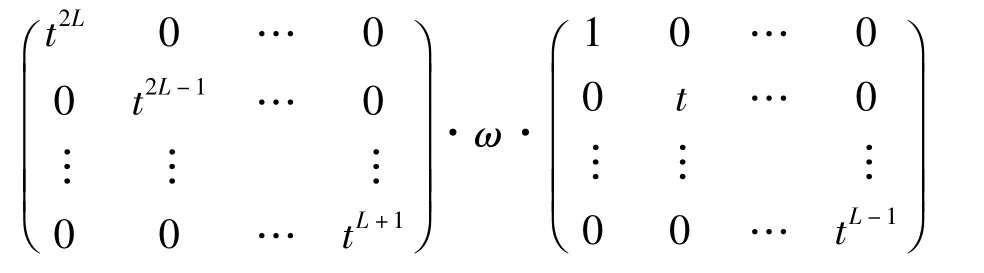
这里

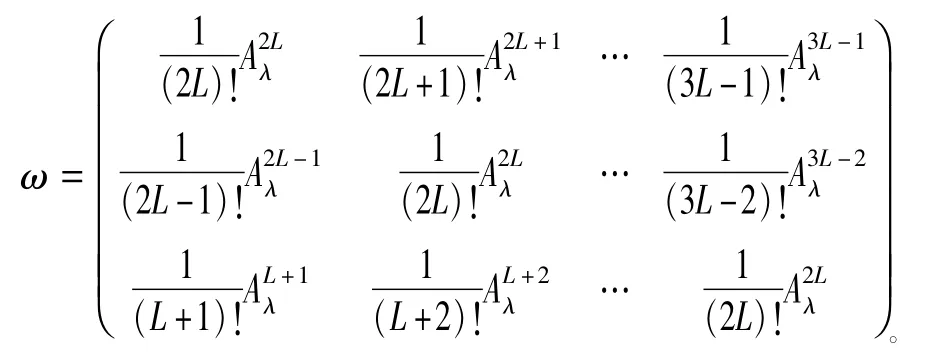
由Aλ≜λA（λC-A）-1及引理1.2的证明过程可知ω可逆。所以，

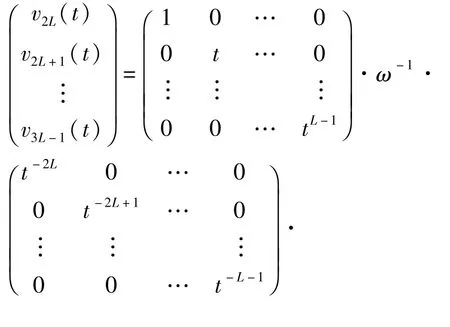
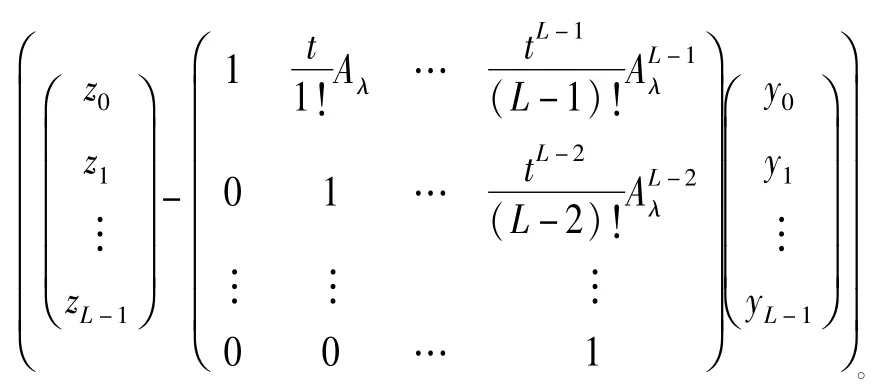
容易看出存在一个常数C1，使得

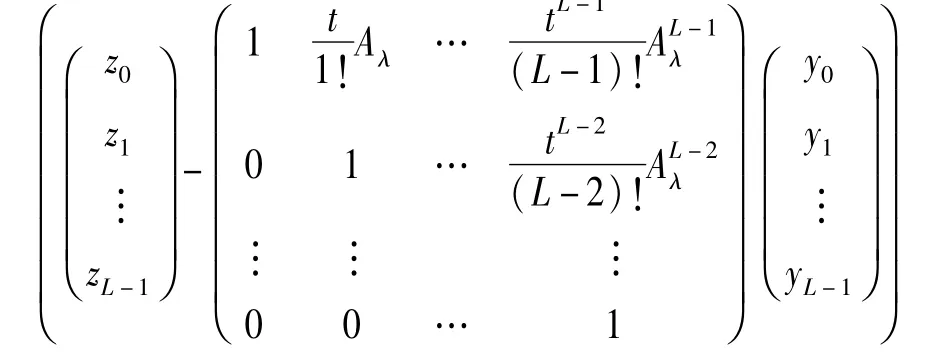
的所有系数是有界的，并且其界为C1t-L-i-1。由引理1.2的证明可知，∃一个常数C2，使得

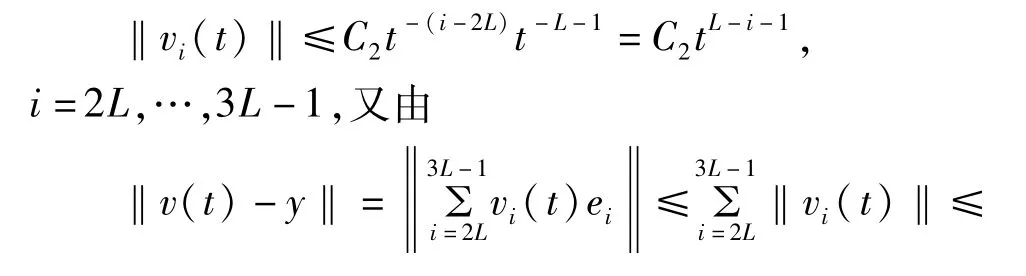
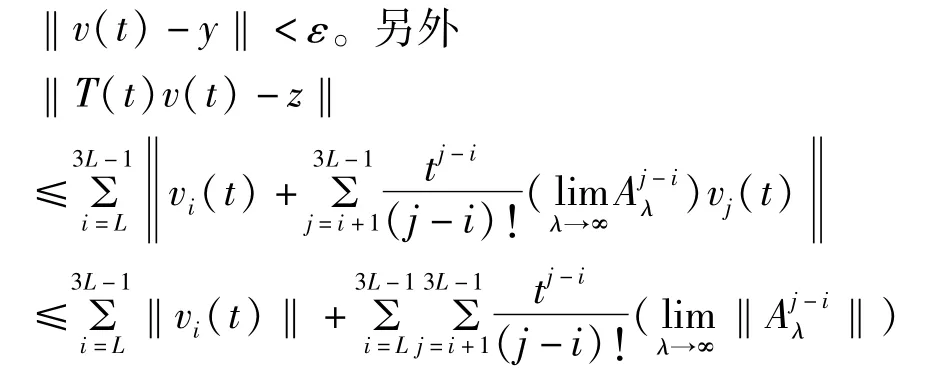
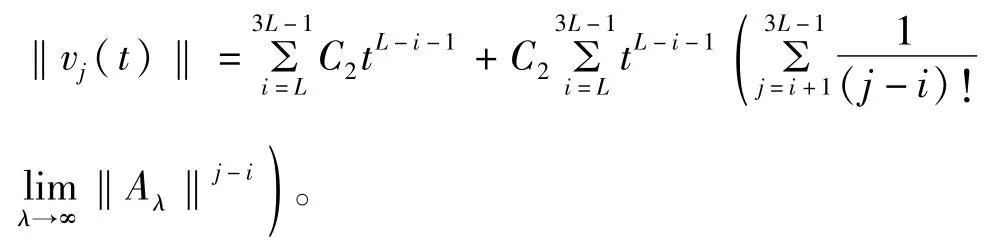
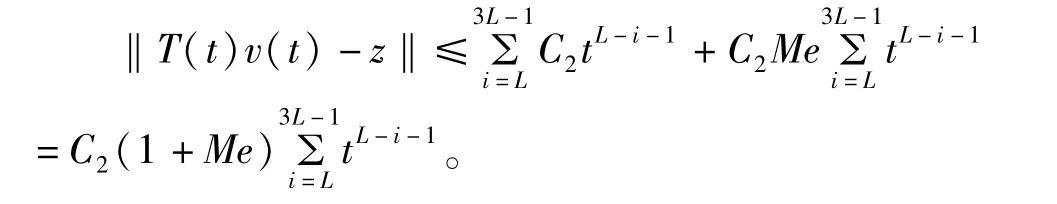
因此，对∀ε＞0，∃t2＞0，使得当t≥t0时有‖T（t）v（t）-z‖＜ε。定理得证。

［1］王宗毅.广义C0-半群的生成元和扰动［J］.惠州学院学报，2002（3）：11-15.

［2］姚玉武，刘恒，胡秀林.Banach空间上强混合的C0-半群［J］.数学年刊A辑（中文版），2010，（02）.

［3］Ovsepian R I，Pelczynski A.On the existence of a fundamental total and bounded biorthogonal sequence in every separable Banach space，and related constructions of uniformly bouneded orthonormal systems in L2［J］.Studia Math，1975，54：49-159.

［4］姚玉武，史恩惠，周友成.Banach空间上强混合算子［J］.数学年刊，2006，27A（2）：189-196.

［5］Pazy A.Semigroups of Linear Operators and Applications to Partial Differential Equations［M］.Springer-Verlag，New York Berlin Heidelberg Tokyo.

［6］Zaidman S.Topics in abstract differential［J］.London：Longman Scientific anc technical.1994.

［责任编辑 贺小林］

The Strongly M ixing Generalized C0-Sem igroup on Banach Spaces

GAO FENG，ZHAO Hua-xin
（College of Mathematics and Computer Science，Yan an university，Yan an 716000，China）

On the basis of traditional stronglymixing C0-semigroup，the paper gives the definition of the strongly mixing generalized C0-semigroup，and uses its basic properties，it is shown that every separable infinite dimensional complex Banach space admits a stronglymixing generalized C0-semigroup.

strongmixing；generalized C0-semigroup；Banach space

O177.2

A

1004-602X（2011）04-0001-03

2011 09 16

高 峰（1984—），女，陕西榆林人，延安大学在读硕士研究生。