n维非线性系统稳定性若干定理的推广

付 华，秦宏立，周居政

（延安大学数学与计算机科学学院，陕西延安 716000）

n维非线性系统稳定性若干定理的推广

付 华，秦宏立，周居政

（延安大学数学与计算机科学学院，陕西延安 716000）

利用Gronwall-Bellman不等式，对Lyapunov函数的限制条件作了适当的改进，得到了n维非线性系统平凡解稳定性的若干定理，从而推广了相应文献的已有结果。

Lyapunov函数；稳定性；渐进稳定性；一致稳定性

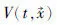
1 预备知识

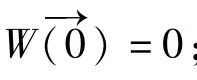
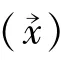
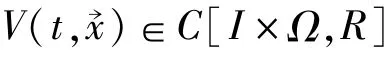
定义4［3］设非线性系统

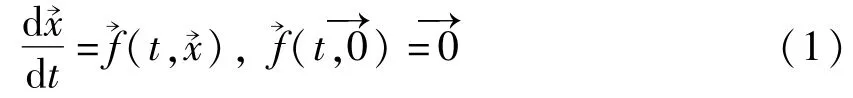
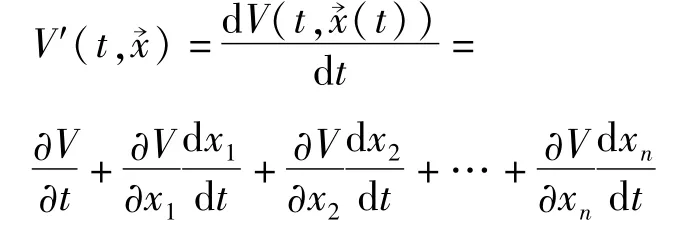
引理［3］（Gronwall-Bellman不等式） 设t≥t0，u（t）≥0，f（t）≥0；u（t），f（t）∈C［I，R+］，R+=［0，+∞］，且t≥t0满足

2 主要结果

考虑非线性系统：

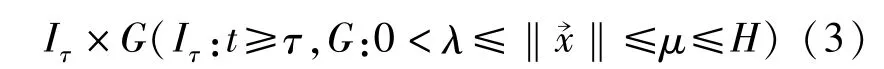
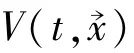
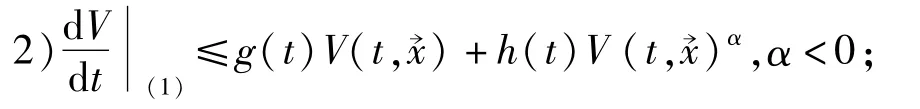
其中g（t），h（t）非负可积且在［τ，+∞）上积分收敛，则方程（1）的零解稳定。

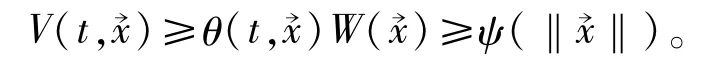
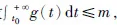
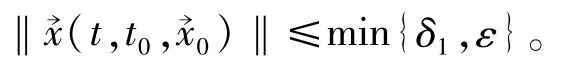
（b）当t≥T时，由定理条件2）得

从T到t积分上式得

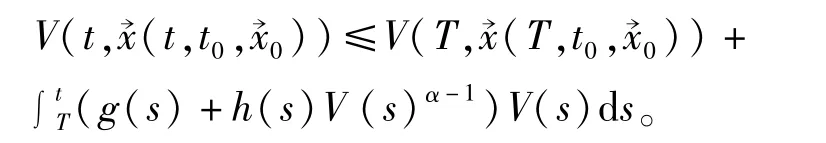
由引理1知

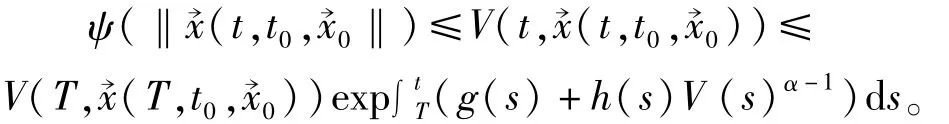
因为

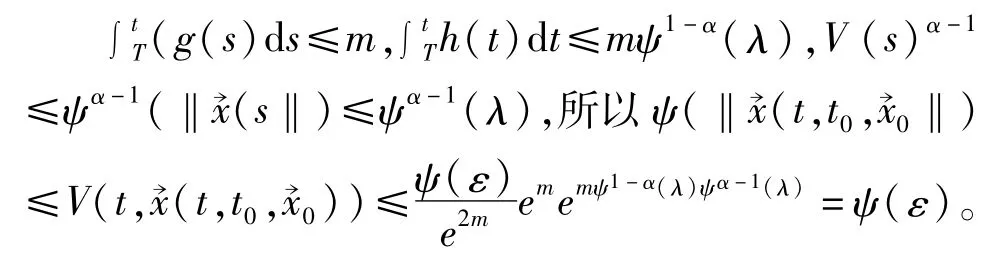
又因为ψ∈k，故

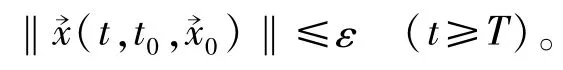
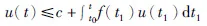
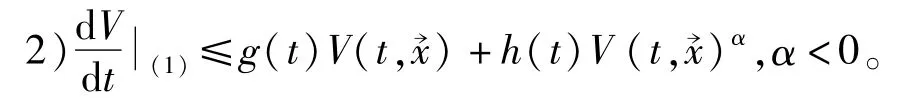
其中g（t），h（t）非负可积且在［τ，+∞）上积分收敛，则方程（1）的零解渐进稳定。

证明 从定理1可知，方程（1）的零解稳定，以下我们只需证明系统（1）平凡解是吸引的。

由题设条件1）知，存在ψ∈k使

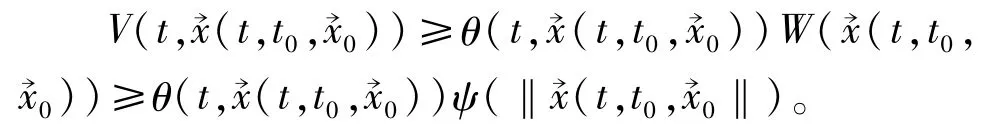
由题设条件2），类似定理1的证明可得

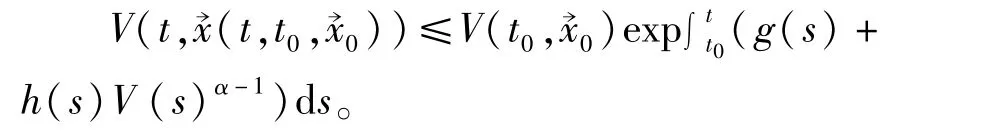
（其中m为某正数）。

由此可得

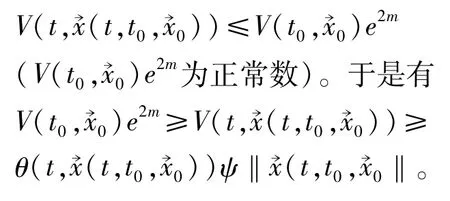
这样就证明了方程的零解是吸引的，从而也就证明了系统（1）的零解渐进稳定。

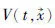
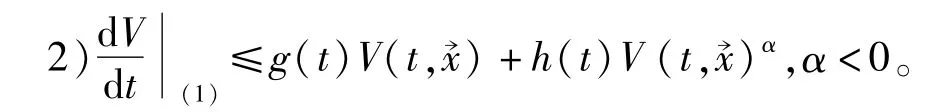
其中g（t），h（t）非负、可积且在［τ，+∞）上积分收敛。

则系统（1）的零解一致稳定。

证明 对任意ε＞0，由题设条件1）知，存在函数ψ1，ψ2∈k使

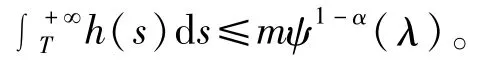
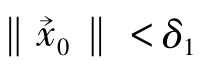
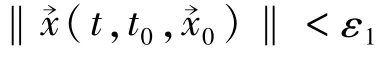
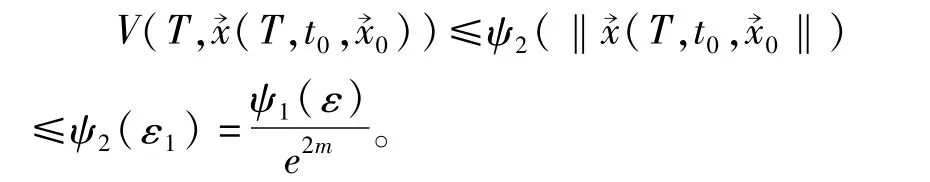
对t≥T，由题设条件2）及引理1得

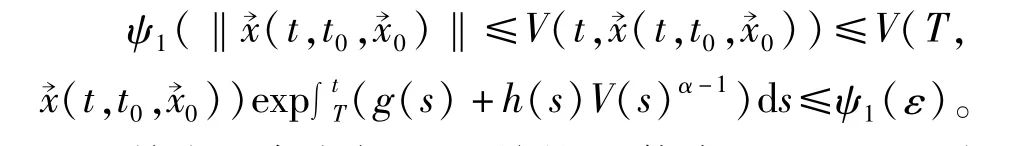
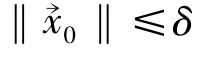
（b）当t0≥T时，同（a）的证明得

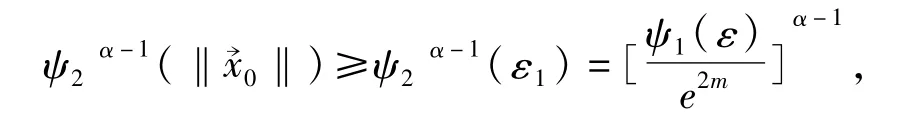
所以得

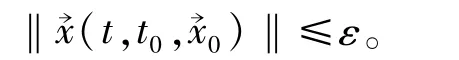
故由题设条件1）与2）知系统（1）的平凡解一致稳定。

［1］吕玉华.Lyapunov稳定性理论若干定理的推广［J］.工程数学学报，2003，20（1）：127-130.

［2］高莲，包曙红.关于Lyapunov稳定性若干定理的推广［J］.内蒙古师范大学学报（自然科学汉文版），2006，35（4）：407-412.

［3］廖晓昕.稳定性的数学理论及应用［M］.武汉：华中师范大学出版社，1988.

［4］徐润.关于李亚普诺夫稳定性若干定理的推广［J］.沈阳师范大学学报，2003，21（2）：87-90.

［5］高莲.关于Lyapunov稳定性理论若干定理的推广［D］.硕士学位论文，2005.

［6］徐道义.关于稳定性的几个基本定理［J］.数学季刊，1992，7（2）：61-67.

［7］胡芬.关于零解稳定和一致稳定的几个判别定理［J］.通化师范学院学报，2008，29（4）：15-17.

［8］王瑞莲.关于微分方程稳定性理论若干定理的推广［J］.内蒙古财经学院学报（综合版），2010，8（5）：143-145.

［责任编辑 贺小林］

The Generalization of Theorem s about Stability of n-dimensiond Norlinear System s

FU Hua，QIN Hong-li，ZHOU Ju-zheng
（College of Mathematics and Computer Science，Yan an University，Yan an 716000 Shanxi）

By using the Gronwall-Bellman inequality the limiting conditions of the lyapunov function were improved.Some theorems about the stability for the trivial solution of the n-dimensional and nonlinear systems were obtained，and several decision theorems of the related literatureswere extended.

Lyapunuov functions；stability；gradual stability；uniform stability

O175.13

：A

：1004-602X（2011）04-0006-03

20110917

付 华（1985—），男，陕西靖边人，延安大学在读硕士研究生。