Artin A-半单环探究

田 岩，张力宏，张秋雨，刘 岩

(吉林师范大学 博达学院，吉林 四平 136000)

1 A-内射模及其性质

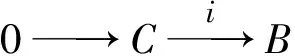
图1 A-内射模图象 图2 A-内射模的交换图

易见，内射模是A-内射模.另外由定义1，可得

命题1 左R-模M是A-内射模当且仅当对正合列

0→C→B→A→0，

有正合列

0→HomR(A，M)→HomR(B，M)→HomR(C，M)→0，

其中B是Artin模.

命题2 左R-模M是A-内射模当且仅当有交换图2，其中R是Artin环，I是R的任意左理想.

证明 “⟹”显然.

“⟸”考虑图3，其中B是Artin模，C是B的子模，令Ω={(C'，β')|其中C⊆C'⊆B，β'是α在C'上的扩张}，由于Artin模关于子模封闭，所以Ω非空，定义(C'，β')<(C''，β'')⟺C'⊆C''⊆B，且β''是β'在C''上的扩张，则Ω是偏序集且满足Zorn's引理，从而有极大者(C0，β0).

若C0=B，则结论成立.假设C0≠B，则有

0≠x∈BC0.令I={r∈R|rx∈C0}，

则I是R的左理想.定义h:I→M，r→β0(rx)，则由已知，有同态映射h':R→M，是h在R上的扩张.

令C1=C0+Rx⊆B，则C0⊂C1，定义

β1：C1→M，a0+rx→β0(a0)+rh(1)，

其中a0∈C0，1∈R是单位元.如果

a0+rx=a'0+r'x，a'0∈C0，r'∈R，

有(r-r')x=a'0-a0∈C0，得

r-r'∈I，β0((r-r')x)=β0(a'0-a0)=

h(r-r0)=h(r-r0)=(r-r0)h'(1)，

从而

β0(a'0)+r0h'(1)=β0(a0)+rh'(1)，

说明β1是良定义的模同态映射，且β0(a0)=β1(a0)，得(C1，β1)∈Ω，且(C0，β0)<(C1，β1)，这与(C0，β0)的取法矛盾，所以C0=B，由定义1知M是A-内射模.

图3 A-内射模图象

命题3 A-内射模关于直积，直和项封闭.

证明 设{Mi|i∈Ω}是左R-模，A是任意左R-模，由[1]中定理2.6，有

HomR(A，∏Mi)≅∏HomR(A，Mi)

设0→C→B→A→0是任意左R-模短正合列，有交换图4.

图4 正合列交换图

其中B是Artin模，顶行，底行正合，α，β，γ同构.反复应用命题1，可证得A-内射模关于直积，直和项封闭.

2 A-投射模及其性质

定义2 设M是左R-模，若对任何正合列

其中B是Artin模，任何模同态α：M→A，有β：M→B，使α=πβ，则称M为A-投射模.(图5).

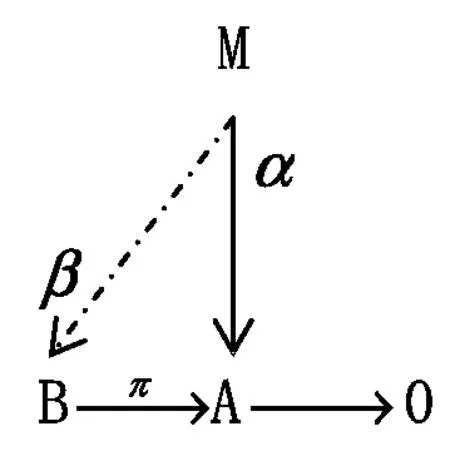
图5 A-投射模图象

易见，投射模是A-投射模.由定义2，易得

命题4 左R-模M是A-投射模当且仅当对正合列

其中B是Artin模，有正合列

0→HomR(M，C)→HomR(M，B)→HomR(M，A)→0.

命题5 A-投射模关于直和、直和项封闭.

证明 设{Mi|i∈Ω}是左R-模簇，N是任意左R-模，则由[1]中定理2.4，有

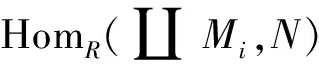
设0→A→B→C→0是任意左R-模短正合列，有交换图6.

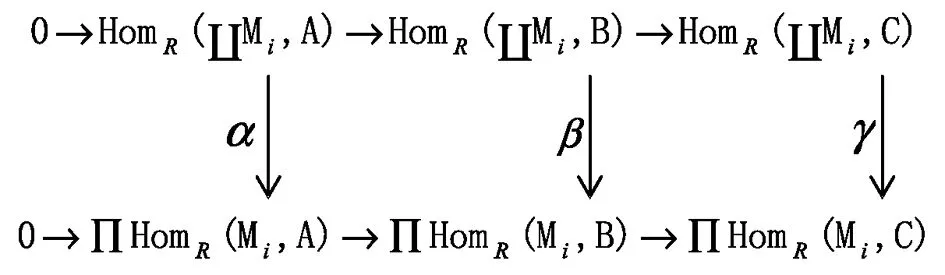
图6 正合列的交换图

其中B是Artin模，顶行，底行正合，α，β，γ同构.反复应用命题4可知，对每个i∈Ω，Mi是A-投射模⟺底行是短正合列⟺顶行是短正合列⟺ЦMi是A-投射模.可证得A-投射模关于直和、直和项封闭.

3 A-半单环

定理1 对于环R，以下命题等价:

i)每个左R-模是A-投射模;

ⅱ)每个左R-模是A-内射模;

ⅲ)A-内射模关于子模封闭;

ⅳ)A-投射模关于商模封闭;

ⅴ)每个Artin模的子模是其直和项;

ⅵ)每个Artin模都是半单模;

ⅶ)对于每个Artin模A，有Soc(M)=M;

ⅷ)对于每个Artin模A，有J(A)=0.

证明 ⅰ)⟹ⅱ)考察图7，其中B是Artin模，由已知A是A-投射模，所以底行可裂，从而有β是α的扩张.

ⅱ)⟹ⅰ)考察图8，E是Artin模，由已知B是A-内射模，所以底行可裂，存在λ：A→E，使1E=λπ.存在β=λ∂，其中β:M→E，因为πβ=πλα，所以α=πβ，图形可交换，故M是A-投射模.

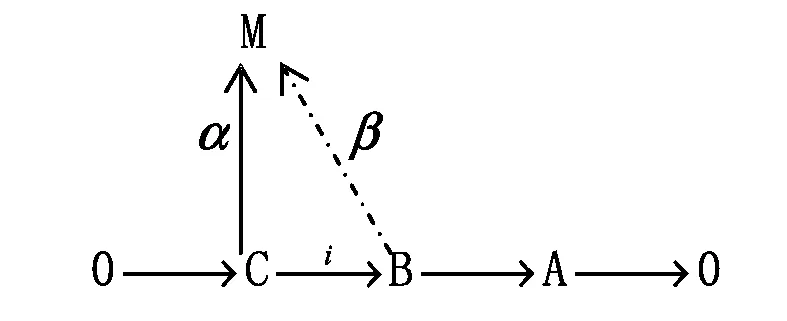
图7 模扩张图象

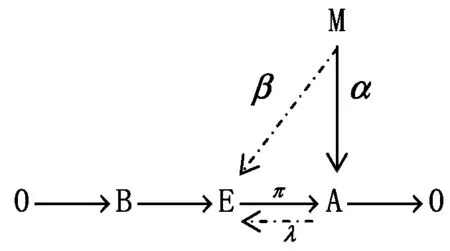
图8 A-投射模的交换图

图9 正合列可裂的交换图

ⅱ)⟹ⅲ) 显然成立.

ⅲ)⟹ⅱ) 设M是左R-模，E(M)是M的内射包，当然是A-内射模，由已知，M是A-内射模.

ⅰ)⟹ⅳ) 显然成立.

ⅳ)⟹ⅰ) 设M是左R-模，则有正合列P→M→0，其中P是投射模，当然是A-投射模，由已知M是A-投射模.

ⅰ)⟹ⅴ) 设左R-模正合列0→C→B→A→0，其中B是Artin模，

由已知A是A-投射模，所以正合列可裂，得C是B的直和项.

ⅴ)⟹ⅰ) 考察图9，其中B是Artin模，由已知，底行可裂，所以有λ:A→B，使πλ=1A，令β=λα，则πβ=πλα=α，得i)成立.

ⅴ)⟹ⅵ) 设M是Artin模，若M的每个子模都是其直和项，由[2]中命题2，4知M是半单模.

ⅵ)⟹ⅴ) 设M是Artin模，若M是半单模，再由[2]中命题2.4，M的每个子模都是其直和项.

ⅵ)⟹ⅶ) 若M是Artin半单模，则M=M1⊕M2⊕M3⊕…Mn，Mi是M的极小子模，再由Soc(M)的定义，有Soc(M)=M.

ⅶ)⟹ⅵ) 设M是Artin模，且Soc(M)=M，由[3]中推论9.1.3，Soc(M)是M的最大的半单子模，所以M是半单模.

ⅵ)⟺ⅷ) 由[4]中命题10.15显然.

定义3 称满足以上等价条件的环R为A-半单环.

显然，半单环是A-半单环.

参考文献：

[1]J.Rotman.An Introduction To Homological Algebra[M].London:Academic Press，1979.

[2]薛伯英.基础环论[M].长春:吉林大学出版社，1993.

[3]F.Kasch.Modules And Rings[M].London:Academic Press Inc.LTD.1982.

[4]F.W.安德森 K.R.富勒尔.环与模范畴[M].北京:科学出版社，2008.

[5]张力宏，王秀丽.关于Noether N-半单环[J].吉林师范大学学报，2004(2).

[6]班和秀，黄容伟.N-半单环、Noether N-半单环和几类特殊环[J].南阳师范学院学报，2006(9).

[7]刘绍学.环与代数[M].北京:科学出版社，2001.