圆环线匝构成的平面共模EMI滤波器的特性研究

王世山 朱 叶 周小林 武丽芳

（南京航空航天大学自动化学院 南京 210016）

1 引言

平面EMI滤波器以其体积小、高频性能好等优点而在电力电子领域有着较好的应用前景。它实现了电感、电容等无源元件的集成，可以明显减少无源元件的数量，进而减小整个装置的体积。目前，平面EMI滤波器主要有两种实现方法，一种是由弗吉尼亚理工大学（Virginia Polytechnic Institute and State Universit）陈仁刚博士提出的基于矩形平面LC线圈来实现[1]，主要是降低了滤波器的高度；另一种是由浙江大学伍晓峰等提出的基于柔性带材绕组来实现[2]，主要是减小了滤波器的占地面积。两者均处于研究阶段，还未实现在功率电路中的应用。因此，平面EMI滤波器有着潜在的研究价值，本文主要针对前者进行研究。

文献[1]中首次将平面LC线圈应用于EMI滤波器中。矩形平面LC线圈的结构如图1a所示，它是在介质基板的两表面直接喷镀绕组导体形成的，加高磁导率的磁心后便可以产生足够大的分布电感和电容，通过适当的连接可以实现串联谐振、并联谐振和低通滤波器等结构[3]。

但随着现代电力电子向高频率方向发展，电流在导线直角拐角处分布很不均匀，严重影响滤波器的性能。本文类比电力设备中导线的布置和排列，首次提出了采用具有光滑特性的环形PCB导线组成的平面LC线圈结构（见图1b），使线圈中电流分布更加均匀，从而提高滤波器的性能。同时采用罐形磁心，导体全部位于磁心内部，导体利用率高，且抗外界电磁干扰能力强。

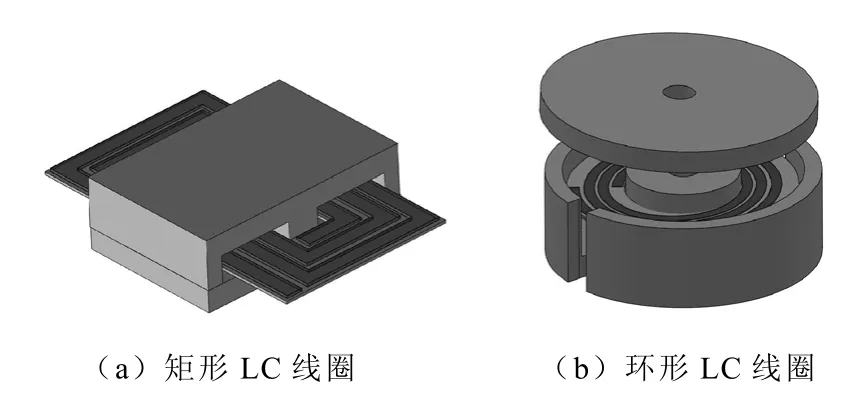
图1 带磁心的平面LC线圈Fig.1 Planar LC coil with magnetic core

由于集成无源元件的分布参数结构，使得其设计和分析成为难点。文献[3-4]中利用广义多导体传输线理论建立了平面集成LC线圈的高频模型，将其等效为标准的直线型传输线，然后进行级联，可以得到较为准确的阻抗特性，然而在平面EMI滤波器的设计中，其性能的主要指标是插入损耗，阻抗特性不能直观的反映出其高频性能。文献[5]在集成EMI滤波器的设计时，仅仅计算出了低频时等效的集总电感和电容，高频时存在很大误差，造成高频插入损耗不能满足要求。文献[2]中准确地计算了基于柔性PCB集成滤波器的插入损耗，但该模型不适于平面集成滤波器。

鉴于以上原因，本文在分析了基于环形平面LC线圈构成的共模EMI滤波器结构的基础上，通过将平面LC线圈展开成有限个单元的级联，建立了集成LC线圈的等效集中参数电路，考虑了匝间寄生电容、磁心磁导率的非线性及导体之间的磁耦合，基于节点电压法求解了当其连接成共模滤波器时的插入损耗，可以更加直观地了解其高频性能。

2 平面LC线圈的有限元分析

为了研究平面LC线圈中电流及其所产生的磁密分布情况，分别以平面EI型磁心PEI43和罐形磁心P43为例，通过Maxwell3D仿真软件建立3D有限元模型。由于结构的对称性，只建立1/2模型，选择静磁场求解器，取计算误差在1%以内。

2.1 有限元模型的边值问题

不同媒质间的交界面满足自然边界条件，即跨越物体间界面的磁场强度H的切向分量和磁感应强度B的法向分量是连续的，并满足关系[6]

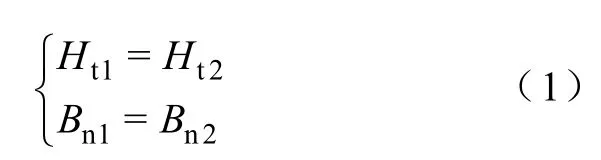
式中，Ht为分界面处磁场强度的切向分量，Bn为分界面处磁感应强度的法向分量。

选择矢量磁位A为自由度时，泛定方程为

式中，μ为磁导率，J为电流面密度，根据导体中施加电流I确定。

同时，空气外表面近似满足齐次第二类边界条件

由上述边值问题，可以剖分整个求解区域，求解得到各节点的矢量磁位A，磁感应强度B和磁场强度H可以根据式（4）得到。

2.2 仿真分析

导体中电流密度分布如图2所示。

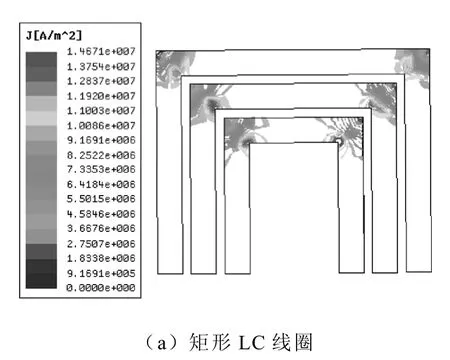
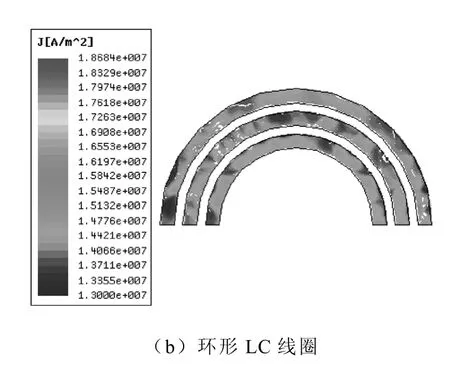
图2 线圈PCB导体的电流面密度分布Fig.2 Current density distribution in conductor of coil

从图2中可以看出，矩形线圈导体的拐角处，电流分布很不均匀，在内角处电流密度很大，而在外角处电流密度很小，而环形线圈导体中的电流呈均匀分布。

平面LC线圈产生的磁通密度分布如图3所示。

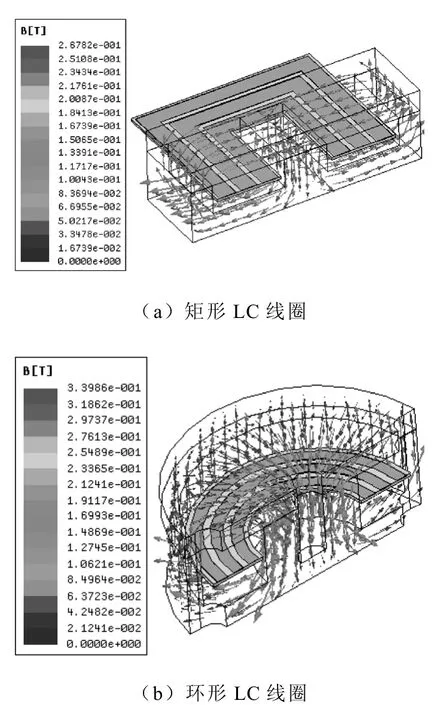
图3 不同线圈产生的磁通密度分布Fig.3 Magnetic flux density distribution in different coils

如图3所示，矩形LC线圈中磁通密度主要由磁心内部的导体产生，大部分磁通流经磁心内部，磁心外部导体周围的磁通密度几乎为零，而环形LC线圈的导体周围的磁通均匀分布，均产生较大的磁通密度。因此，提高了导体的利用率。

3 平面共模EMI滤波器的插入损耗

3.1 平面共模EMI滤波器的组成

分立元件构成的共模EMI滤波器及其等效电路如图4所示，在共模激励下，可以等效为两个并联的低通滤波器。

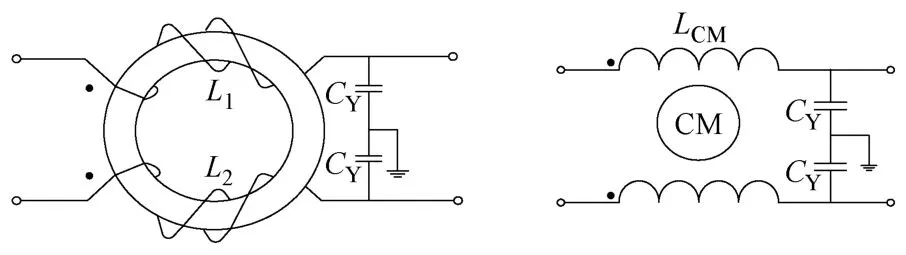
图4 分立元件构成的共模EMI滤波器及其等效电路Fig.4 CM filter EMI consisting of discrete components and its equivalent circuit

集成LC线圈是一个分布参数结构（见图5），对于单个线圈，当A1D1点接输入源，C1D1点接负载，可以等效为一个低通滤波器结构[7]。因此，平面共模滤波器可以通过两个集成LC线圈并联实现（见图5a），加磁心后结构如图1b所示，图5b为其等效集中参数电路。

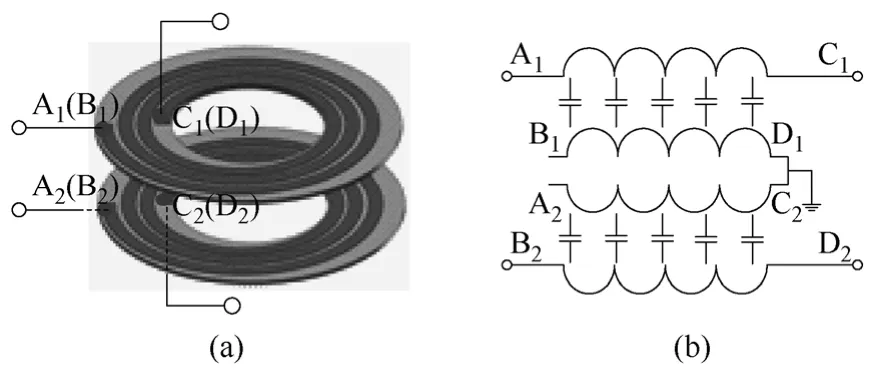
图5 平面共模滤波器及其等效电路Fig.5 Planar CM filter and its equivalent circuit

3.2 集中参数等效电路

单匝平面LC线圈可以直接展开成直线型（见图6）。其等效集中参数电路由多个电容和耦合电感组成的π型电路级联构成，该电路模型可以用普通传输线理论进行分析。

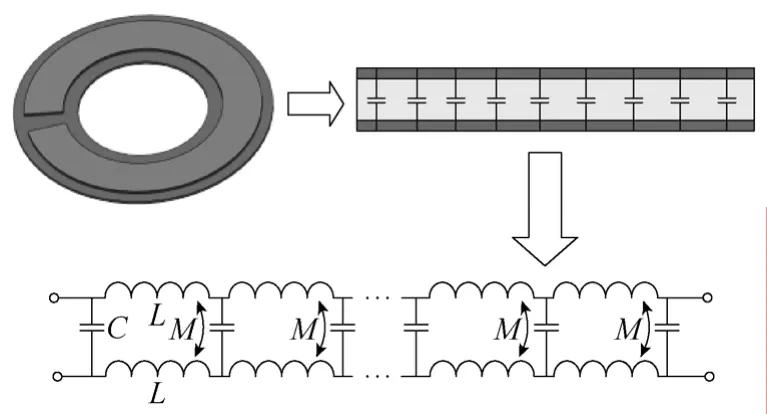
图6 单匝LC线圈的展开Fig.6 Spreading of single -turn for LC coil

线圈为多匝时，由于穿过磁心的磁通耦合全部线圈（见图3b），因此，必须考虑相邻导体之间的耦合互感。为了得到其等效模型，忽略导体损耗及介质材料的损耗。每匝线圈等效为由电容和耦合电感组成的基本单元的级联，所有的电感单元之间均存在电感耦合（见图7），图中只画出了部分互感。

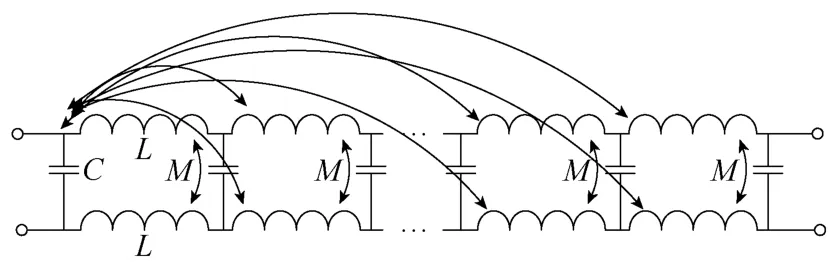
图7 多匝平面LC线圈的等效模型Fig.7 Equivalent model of multi-turn for planar LC coil

一个n匝集成LC线圈连接成低通滤波器结构（见图8），输入电压为US，输入源阻抗为Zin，输出负载为Zout，与测量时线性阻抗稳定网络（LISN）的阻抗相一致，取输入源阻抗和负载阻抗均为50Ω，每匝等效为m个单元。

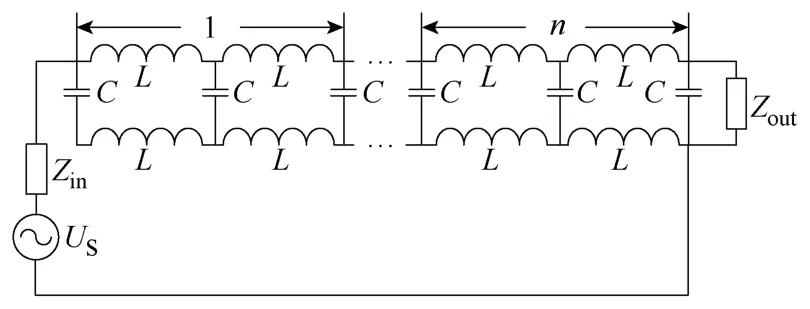
图8 低通滤波器连接方式Fig.8 Connection of low-pass filter

多匝平面LC线圈的同层相邻导体之间存在寄生电容，鉴于介质基板的介电常数非无限大，该电容不能忽略[8-9]。因此，考虑匝间寄生电容CP后，等效模型结构如图9所示。

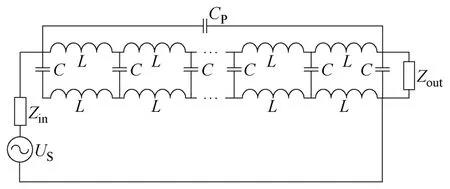
图9 考虑匝间寄生电容后的等效模型Fig.9 Equivalent model considering of parasitic capacitance among turns

3.3 插入损耗特性

3.3.1 磁心磁导率的非线性

EMI滤波器通常使用高磁导率的磁心，高频时磁导率随频率变化很大。因此，将有效磁导率用复数表示：

此外，罐形磁心分为两部分，不可避免的会产生气隙，未经过精密磨光的磁心气隙长度为3～6μm，很小的气隙就会造成有效磁导率的严重下降，图10表示了气隙对磁导率的影响[10]。

由此可见，气隙对有效磁导率的影响很大。下面采用图11所示的等效模型，利用阻抗测量法得到磁心的有效磁导率[11]。

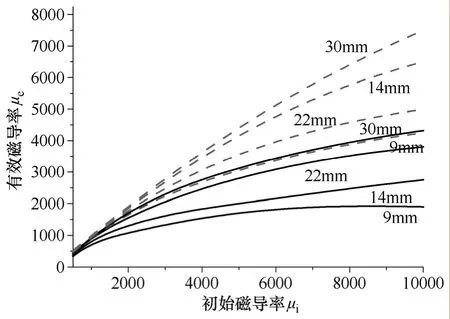
图10 气隙对有效磁导率的影响实线—3μm的气隙长度 虚线—1μm的气隙长度Fig.10 Effective permeability via gap

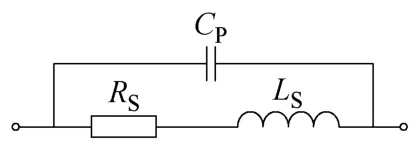
图11 电感器的等效模型Fig.11 Equivalent model of inductor

CP为匝间寄生电容，该电容可以通过测量得到。据图11中模型得到的电感器阻抗为

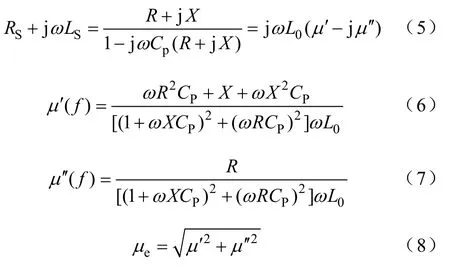
式中，L0为空心线圈时的电感量。

通过仪器（例如网络分析仪HP4395A）测量磁心电感阻抗的实部和虚部，得磁导率如图12所示。

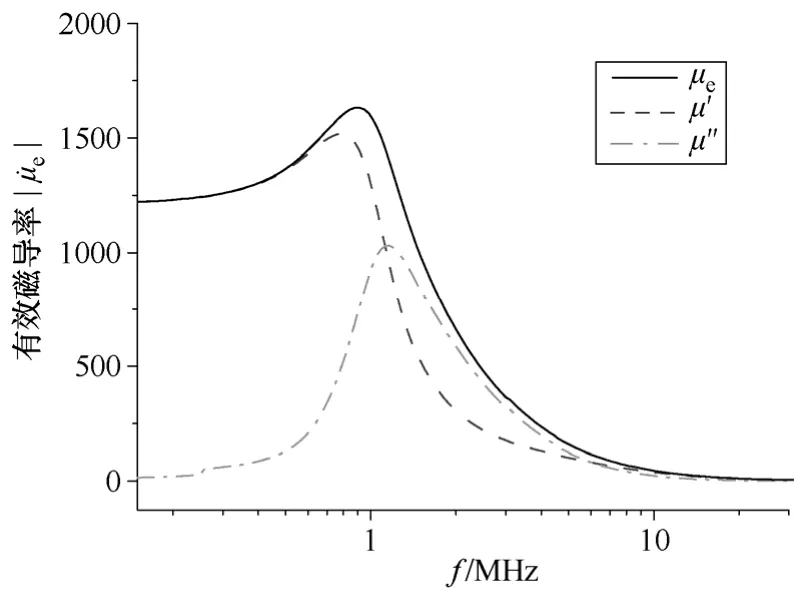
图12 磁心的有效磁导率Fig.12 Effective permeability of magnetic core

3.3.2 电磁参数

每个单元的等效电容C为

式中，S为PCB导体的正对面积；d和εr分别为介质层的厚度和相对介电常数；m为每匝等效单元数。

每个单元的自感为

式中，Ae和le分别为磁心的有效磁路面积和有效磁路长度。

任意两导体单元间的互感为[12]

式中，kij为导体i和j间的耦合系数，i=1,2,…,n，j=1,2,…,n，且i≠j。

3.3.3 插入损耗的计算

电路模型有多个相同的π 型单元级联而成（见图13），图13按规律标明了节点和支路的序号，A和Z分别为电路的关联矩阵和阻抗矩阵。

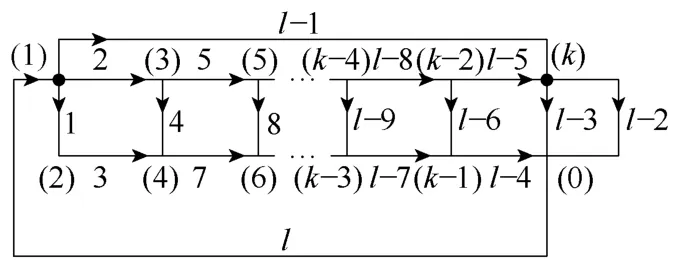
图13 等效电路拓扑结构Fig.13 Equivalent topological structure

节点电压方程为

据式（12）可以得到节点k的电压，则插入损耗

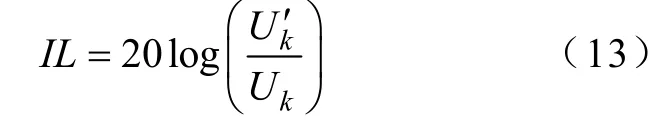
4 实验验证

基于环形LC线圈的等效集中参数电路，利用节点电压法可以近似预测其插入损耗特性。为验证预测的准确性及不同参数对插入损耗的影响程度，采用两个3匝的环形LC线圈，设计了一台平面共模EMI滤波器，测量小信号条件下的插入损耗，与理论值进行比较。

平面共模EMI滤波器如图14所示，磁心选择罐形磁心P43，初始磁导率为2000，为了减小滤波器的高度，将罐形磁心的一半磨成平面结构。

图14 平面共模EMI滤波器Fig.14 Prototype of planar CM EMI filter

下表是滤波器相关参数，插入损耗的测量可以通过网络分析仪Agilent 4395A结合S参数测试87511A实现。

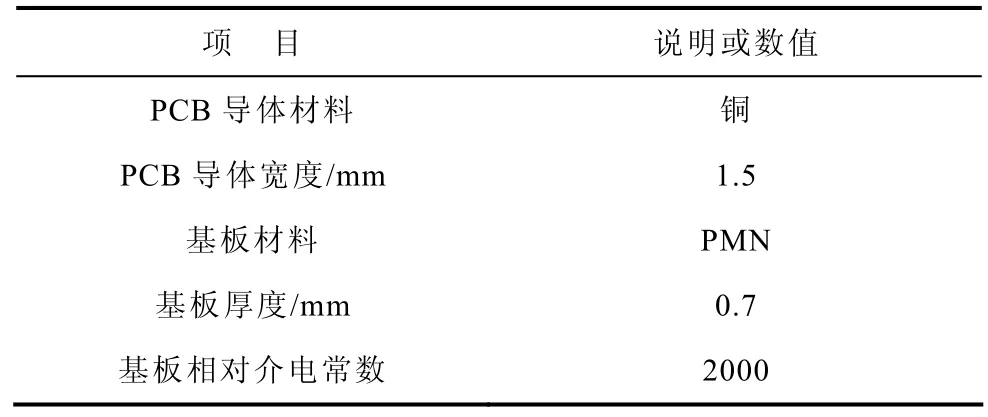
表 平面CM滤波器相关材料和参数Tab.Parameters of planar CM filter

考虑磁心的非线性，据图8和图9中的模型计算其插入损耗值，测量与理论值对比如图15所示。

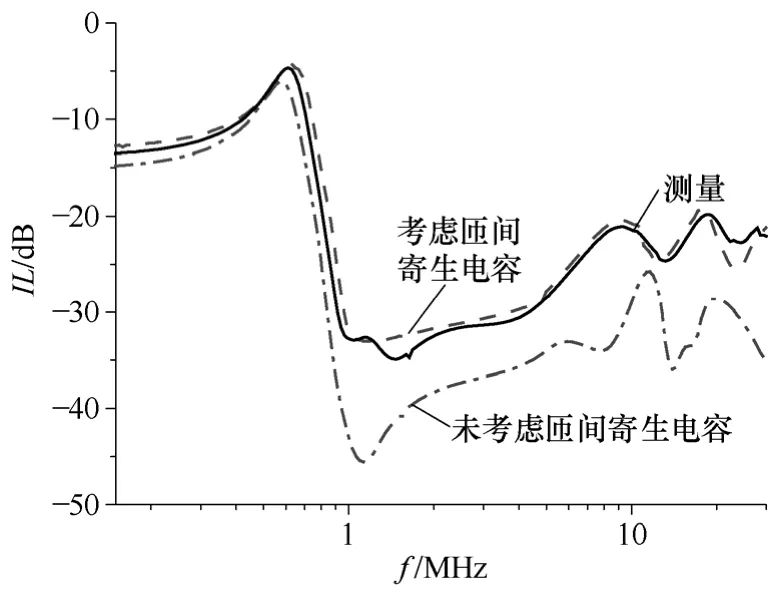
图15 考虑磁导率非线性时的插入损耗值Fig.15 Insertion loss considering nonlinear permeability

图15 显示，未考虑匝间寄生电容，超过0.9MHz时，插入损耗的理论值与测量值相比大约有7dB的降低；而考虑匝间寄生电容以后，在传导频率范围内（0.15～30MHz），理论值与测量值吻合较好。根据图9的模型，在考虑磁心非线性和忽略非线性两种情况下得到的插入损耗值与测量值进行比较，如图16所示。图16显示未考虑匝间寄生电容，超过1MHz时，插入损耗的理论值出现多个谐振点，与测量值差别较大，而考虑磁心非线性后，在传导频率范围内（0.15～30MHz），理论值与测量值吻合较好。

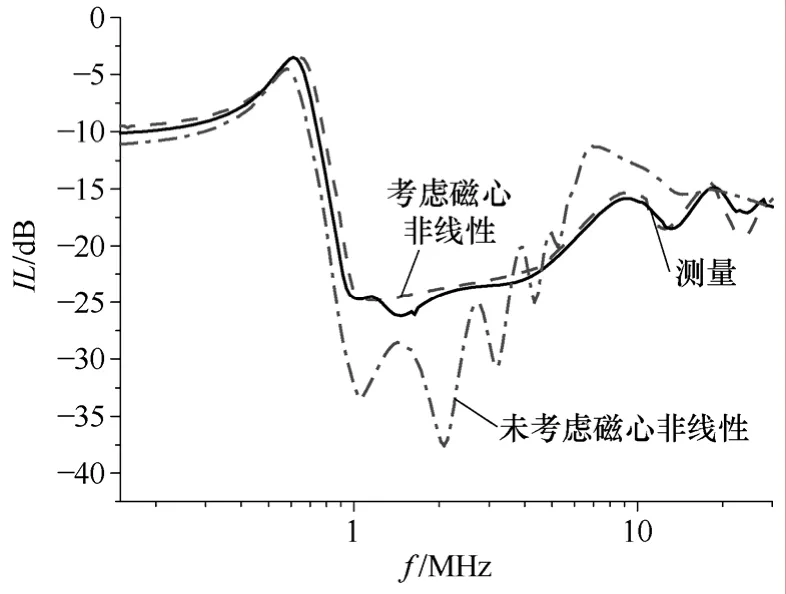
图16 考虑匝间电容时的插入损耗值Fig.16 Insertion loss considering parasitic capacitance

5 结论

本文提出了一种圆环形LC线圈结构，并基于该结构实现了平面共模EMI滤波器。建立了平面LC线圈的等效集中参数电路，考虑了匝间分布电容、相邻导线间的电感耦合及磁心有效磁导率的非线性，设计制作了一台平面共模EMI滤波器，基于节点电压法求解了其插入损耗，并通过测量与模型进行了比较，得到如下三点结论：

（1）通过3D有限元仿真得到，与矩形LC线圈相比，环形LC线圈中电流分布更加均匀，导体利用率更高。

（2）匝间寄生电容对插入损耗有重要影响，在建立其等效集中参数电路时必须考虑匝间寄生电容。

（3）磁心的有效磁导率在高频时呈非线性，使电感也为非线性，进而对高频时的插入损耗产生重要影响。

[1] Chen Rengang,Wyk J D van,Wang S,et al.Planar electromagnetic integrated technologies for integrated EMI filters[C].Proceedings of the IEEE Industry Applications Conference,2003: 1582-1588.

[2] Wu Xiaofeng,Xu Dehong,Weng Zhiwei,et al.Modeling of integrated EMI filter with fiexible multilayer(FML) foils[C].Proceedings of the IEEE Energy Conversion Congress and Exposition,2009:3415-3422.

[3] Zhao Linying,Wyk J D van.Frequency-domain modeling of integrated electromagnetic power passives by a generalized two-conductor transmission structure[J].IEEE Transactions on Circuits and Systems,2004,11(51): 2325-2337.

[4] Zhao Lingyin,Strydom J T,Wyk J D van.The modeling of planar multi-cell integrated reactive components based on multi-conductor generalized transmission structure theory[C].Proceedings of the IEEE Industry Applications Society Annual Meeting,2002: 1787 -1794.

[5] Chen Rengang,Wang Shuo,et al.Integration of EMI filter for distribution power system(DPS) front-end converter[C].Proceedings of the 34th Annual IEEE Power Electronics Specialist Conference,2003:296-300.

[6] 刘国强,赵凌志,蒋继娅.Ansoft工程电磁场有限元分析[M].北京: 电子工业出版社,2005.

[7] Zhao Lingyin,Wyk J D van.Wideband modeling of integrated power passive structures: The series resonator[J].IEEE Transactions on Power Electronics,2004,19(2): 523-530.

[8] 王世山,崔永生,谢少军.铁氧体环形电感器寄生电容的提取[J].电工技术学报,2009,24(4): 22-29.Wang Shishan,Cui Yongsheng,Xie shaojun.Extraction of parasitic capacitance for toroidal ferrite core inductor[J].Transactions of China Electrotechnical Societ,2009,24(4): 22-29.

[9] Wang Shuo,Lee F C,Chen D Y,et al.Effects of parasitic parameters on the performance of EMI filters[C].Proceedings of the 34th Annual IEEE Power Electronics Specialist Conference,2003: 73-78.

[10] Kampczyk V W,RoB E.铁氧体磁心[M].冯怀函,译.北京: 科学出版社,1986.

[11] 阚德鹏,周洁,丁高.EMI滤波电感磁心磁导率的测量方法研究[J].电子质量,2005,31(4): 67-68.Kan Depeng,Zhou Jie,Ding Gao.Research of testing measurement on EMI filtering inductance magnetic core[J].Electronics Quality,2005,31(4): 67-68.

[12] R Paul.电磁兼容导论[M].闻映红,译.北京: 人民邮电出版社,2007.