基于改进Hilbert谱分析的STATCOM并补线路保护方法

刘 青 王增平 张 媛

（华北电力大学电力系统保护与动态安全监控教育部重点实验室 保定 071003）

1 引言

静止同步补偿器（Static Synchronous Compensator，STATCOM）是FACTS家族的重要成员之一，对维持节点电压、抑制电压闪变、阻尼系统振荡以及提高系统暂态稳定性发挥着重要的作用。近年来STATCOM 在电力系统中的应用受到日益广泛的重视，我国自行研制的±20Mvar STATCOM工业样机装置于 1999年已在河南电力公司洛阳站运行，±50Mvar的STATCOM于2006年在上海西郊变电站运行。STATCOM 的重要作用及其较传统设备的优越性使得它在电力系统中应用前景广阔。但是由于STATCOM 的投入使得系统结构变得更加复杂，系统参数随着 STATCOM 的不同运行工况而发生变化。而且故障时由STATCOM产生的谐波和暂态分量，以及STATCOM的投入与切除产生的暂态过程，都会对线路保护的序分量元件、突变量元件和阻抗继电器产生不利影响[1-7]，从而降低了继电保护的可靠性。此外，由于STATCOM本体保护的快速动作使得传统保护的整定变得十分困难，这就对保护的动作速度有了更高的要求。因此，对含STATCOM线路故障时保护测量信号的特征进行深入研究，从而寻求一种适合于并补线路的快速保护方案，对提高继电保护的正确动作率和电力系统运行的可靠性具有重要意义。

希尔伯特-黄变换 HHT（Hilbert-Huang Transform）是一种新的时频信号处理方法[8]。该方法基于信号的局部时间尺度进行分解，无论在时间域还是频率域都具有良好的分辨率，能够更好地反映出信号的局域动态行为和特性，可以准确地检测出突变、非平稳扰动信号的时间、频率和幅值信息，并具有良好的时频聚集性，非常适合对非平稳、非线性信号的分析，已经逐渐应用于电力系统中的信号识别[9-10]、故障信号分析和诊断[11-13]、谐波检测[14]、继电保护[15]和电能质量[16]等领域。

本文利用改进 HHT方法对含 STATCOM的并补线路保护在各种故障暂态时的电流信号进行Hilbert谱分析，并根据故障时Hilbert谱的突变及区内、外故障时的差异，提出了基于Hilbert谱的并补线路单端暂态量保护方案。仿真分析表明，该方案在较低的采样频率下就能有效地区分区内外故障，具有良好的适应性和灵敏性。

2 改进HHT算法

2.1 HHT算法及其缺点

HHT方法由经验模态分解法（Empirical Mode Decomposition，EMD）及Hilbert变换两部分组成。在信号分析中，时间尺度和随时间尺度分布的能量是信号的最重要的两个参数，EMD方法基于信号的局部特征时间尺度，把复杂的信号函数分解为有限的固有模态函数（Intrinsic Mode Function，IMF）之和，使得瞬时频率具有了物理意义。然后再对IMF进行 Hilbert变换，得到每一个 IMF随时间变化的瞬时频率和瞬时幅值，最后得到可以揭示信号内在特征的随时间和频率变化的幅值分布的Hilbert谱。

但是，由于分解算法本身的缺陷，HHT会存在以下缺陷：①EMD分解方法会产生一些低频的与原信号相关性较弱的 IMF，这些 IMF将会在之后的Hilbert谱中产生一些虚假的频率分量。②当被分析信号中含有噪声或异常信号时，分解所得的固有模态函数并不是严格意义上的单模态分量，这使得IMF分量在任一时刻所包含的频率成分并不唯一，各个 IMF分量存在严重的模态混叠现象，所得Hilbert谱不能清晰准确地描述信号能量的时频分布情况。③EMD容易忽略低能量信号成分。

2.2 改进HHT算法

为了消除 HHT算法的模态混叠问题，保证EMD分解所得的各个 IMF分量是严格意义上的单分量信号，本文对分析信号进行预处理，先将信号分解成为多个窄带信号，然后对每个窄带信号进行EMD分解，从而得到一系列可以实施求解瞬时频率的IMF分量构成Hilbert谱。具体步骤如下。

2.2.1 归一化相关性甄别处理

由于相关的 IMF分量 IMFk(t)与剩余信号 rk(t)是原始信号的正交分量，故相关的IMF与原信号会有很强的相关性，而不相关的IMF与原信号的相关性则很弱。据此，依次计算每一个IMF与原信号的相关系数μ，并以此作为甄别相关与非相关 IMF的判别依据。为了避免意外地滤除了能量较小却相关的IMF分量，这些相关系数将进行归一化处理，对于n个IMF的相关系数μi(i=1，2，…，n)，甄别阈值由下式求得

式中，η 是比例因子，推荐经验值为10。每个IMF计算所得的相关系数若大于λ 则得到保留，小于甄别阈值的IMF将被剔除并加入到剩余信号中。这个过程能够去除IMF中与原信号相关性弱的分量，避免Hilbert谱中出现虚假的频率分量。

2.2.2 小波包分解预处理

小波包变换（Wavelet Packet Transform，WPT）具有优秀的正交性、完备性和局部性，可以用来对信号进行预分解，这个过程被称为小波包分解预处理。由于 WPT的分解依据与能量大小无关，故每一个原信号中的频率成分无论其能量大小都将被各个窄带信号保留下来，而不至于使某些能量贡献小的频率分量与其他能量较大的频率分量混杂在一起而被EMD忽略。因此，WPT的引入同时改进了HHT的两个缺陷：保证各个IMF的单分量特性并保留了低能量频率成分。

在对信号进行小波分析时，一般是根据小波函数的连续性、正交性、对称性、紧支撑性和消失矩等属性，并结合被检信号的具体分析要求来选取最佳的小波基函数。通过对目前几种常用小波的各种特性进行对比，结果见表1，由于dbN小波函数的消失矩阶数为 N，阶数越大，小波变换反映的信号高频细节的能力也越强，而且 dbN的支撑长度为2N-1，紧支宽度越窄，小波的局部化特性越好，因此本文选用db4小波。

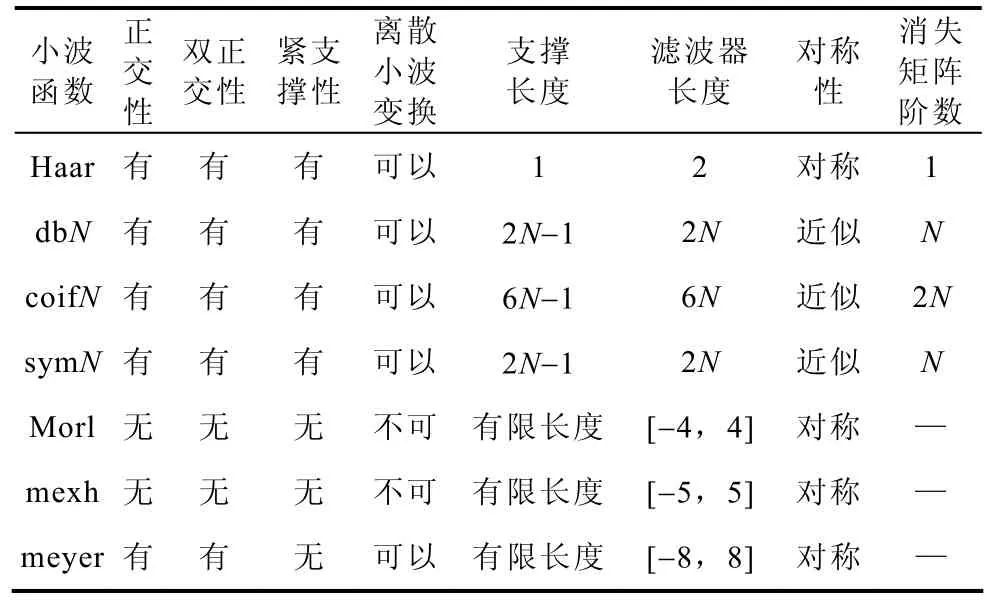
表1 几种常用小波系的主要特征Tab.1 The main character of some wavelets

2.2.3 EMD分解和Hilbert谱分析

经过前两个步骤的信号预处理后，对信号()x t′进行EMD分解，分解后可表示为

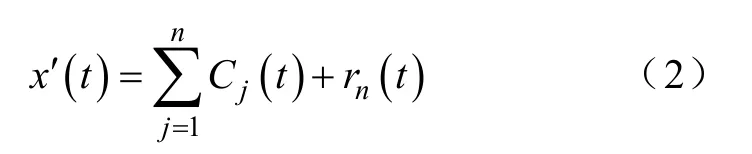
将信号分解成n个 IMF C1(t)，C2(t)，C3(t)，…，Cn(t)和一个剩余分量rn(t)。

然后对 IMF进行 Hilbert变换，求取各分量的瞬时频率和幅值。信号()x t′的Hilbert变换定义为

x′( t)和Y′( t)可组成一复共轭对，得到解析信号

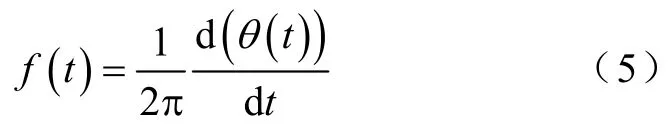
2.3 对改进HHT算法的仿真验证

研究证明，当STATCOM投入运行时，相当于为系统提供了一个谐波干扰源，且采用12脉波的电压源逆变器会产生12k±1次谐波[17]。利用改进HHT算法对图1仿真系统故障时的暂态电压信号进行分析，分解的IMF分量和谱图结果如图2所示。从图中可以看出，故障信号的各次谐波被清晰地分离出来，同时各次谐波在故障前和故障后（故障时刻为0.03s）的变化均能正确反应，证明了改进 HHT方法同样可以有效地用于故障时保护信号的谐波特征的提取和分析。

为了比较原始HHT算法和改进HHT算法的有效性，分别利用原始HHT算法和改进HHT算法对仿真系统投入STATCOM后的电压信号进行仿真分析，结果如图3所示。由于噪声的干扰，运用原始HHT算法不能很好地把各次谐波分离出来，图 3a中的 IMF分量和三维谱图存在严重的频率混叠现象。而图3b中运用改进HHT算法分解的IMF分量从高频到低频依次为23次、13次、11次和基波，表明改进 HHT方法能够准确地将各谐波分量进行分离，很好地消除了由于噪声产生的模态混叠现象。

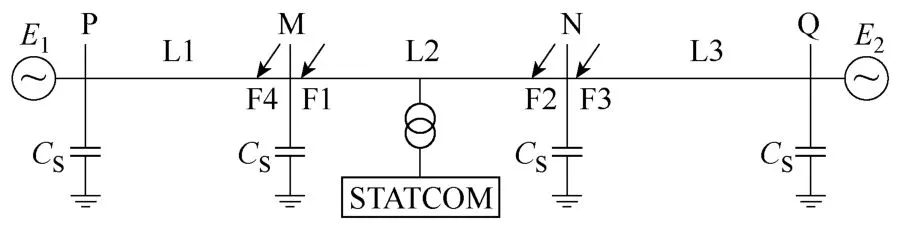
图1 包含STATCOM的双机系统Fig.1 Two-generator system including STATCOM

图2 改进HHT算法对故障暂态信号的谱图分析Fig.2 Transient harmonic analysis based on improved HHT

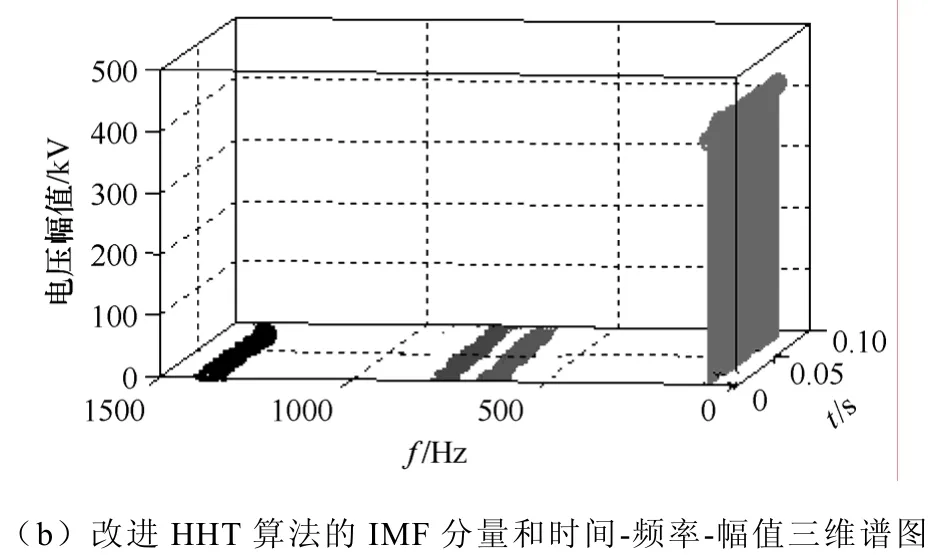
图3 原始HHT算法和改进HHT算法的IMF分量和谱图分析Fig.3 IMF component and the 3d spectrum chart of original HHT and improved HHT

3 含STATCOM并补线路的HHT谱特征分析

3.1 含STATCOM的仿真系统模型

经研究分析表明，STATCOM 安装在线路中点进行补偿是最好的选择，可有效提高系统的暂态稳定性[18]。本文采用PSCAD搭建了如图1所示的含STATCOM的500kV双电源仿真系统。系统中线路L1、L3长度均为 160km，L2长度为 200km，STATCOM安装在L2线路中点，容量为100MVA，连接变压器的漏抗为0.1（pu），采用三相12脉波电压源逆变器。本文均以 L2线路 M侧的保护为例进行仿真分析。故障点设置F1、F2为区内故障，F3、F4为区外故障。其中F1为距M侧保护安装处1km，F2为距保护安装处 199km，F3为正向区外出口 1km，F4为保护反向区外出口1km。由于阻波器能增加高频含量在母线处的衰减程度，提高区内外高频信号的差异，本文采用 XZF-3150-1.0/63-B1型单相阻波器模型：L1=1mH，C1=528pF，L2=0.338mH，C2=3125pF，R=800Ω，工作频率为 48～500kHz。母线对地电容设为 0.1μF。

3.2 并补线路正常运行和故障时HHT谱特征分析

利用改进 HHT算法分别对仿真系统正常运行和故障时的高频谐波进行提取和分析。仿真结果如图4所示。

图 4a和图 4b分别为正常运行和故障时 HHT提取的前三个IMF分量，通过比较表明，正常运行时各IMF分量的分布均匀且幅值较小，而在故障时刻各 IMF分量均发生突变而且幅值变大，反应到Hilbert谱则表现为谱值变大。因此，利用故障时刻HHT谱值的突变可以实现线路故障的判别。

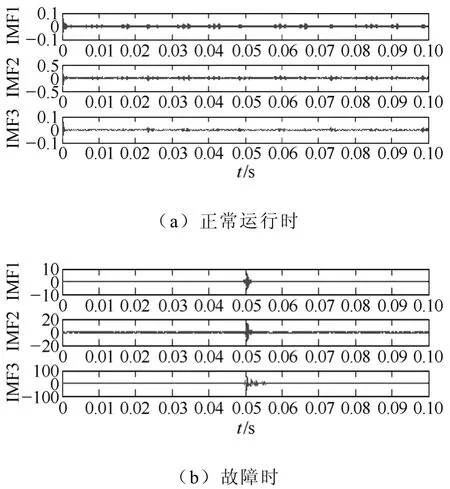
图4 正常运行时和故障时的IMF分量Fig.4 IMF component in normal state and fault state

3.3 并补线路区内和区外故障时HHT谱特征分析

对于含并补元件的输电线路，当发生区内故障时，各个时刻从故障点传播来的暂态电流高频分量由于输电线路分布参数特性而衰减较少，此外，当含STATCOM的线路发生故障时，线路保护测量电压和电流中将会产生较高的谐波成分。因此区内故障时信号的谱值大；当区外故障时，由于母线杂散电容及结合电容的影响使得暂态电流在一个时间段内高频分量得到很大衰减，且频率越高衰减越明显，反应到信号的谱值则表现为较小。以仿真系统 MN线路的M侧保护为例，分别对区内和区外各点发生故障时的故障电流进行 HHT谱分析。故障时刻为0.05s。由于篇幅所限，只给出区内外各故障点发生单相接地故障时的仿真结果如图5所示。

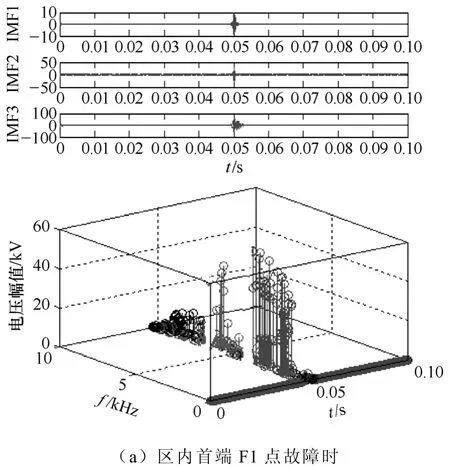
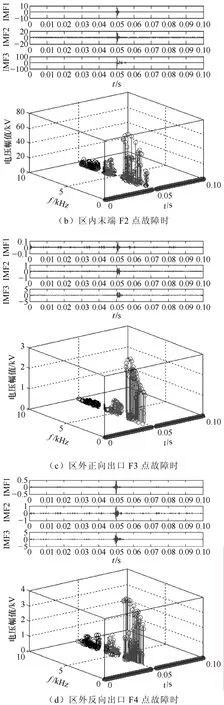
图5 不同故障位置时的IMF分量和HHT三维谱图Fig.5 IMF component and the 3-d spectrum chart of different fault location

比较不同故障点的HHT三维谱图可以看出，改进HHT算法在故障时刻均能准确捕捉到突变；而且区内故障时，F1和F2点的前三个IMF分量的HHT谱值都较大，而区外故障时，F3和F4点的前三个IMF分量的HHT谱值都较小，且与区内故障时谱值的差值很大。其他故障类型也满足此规律，详见表2。

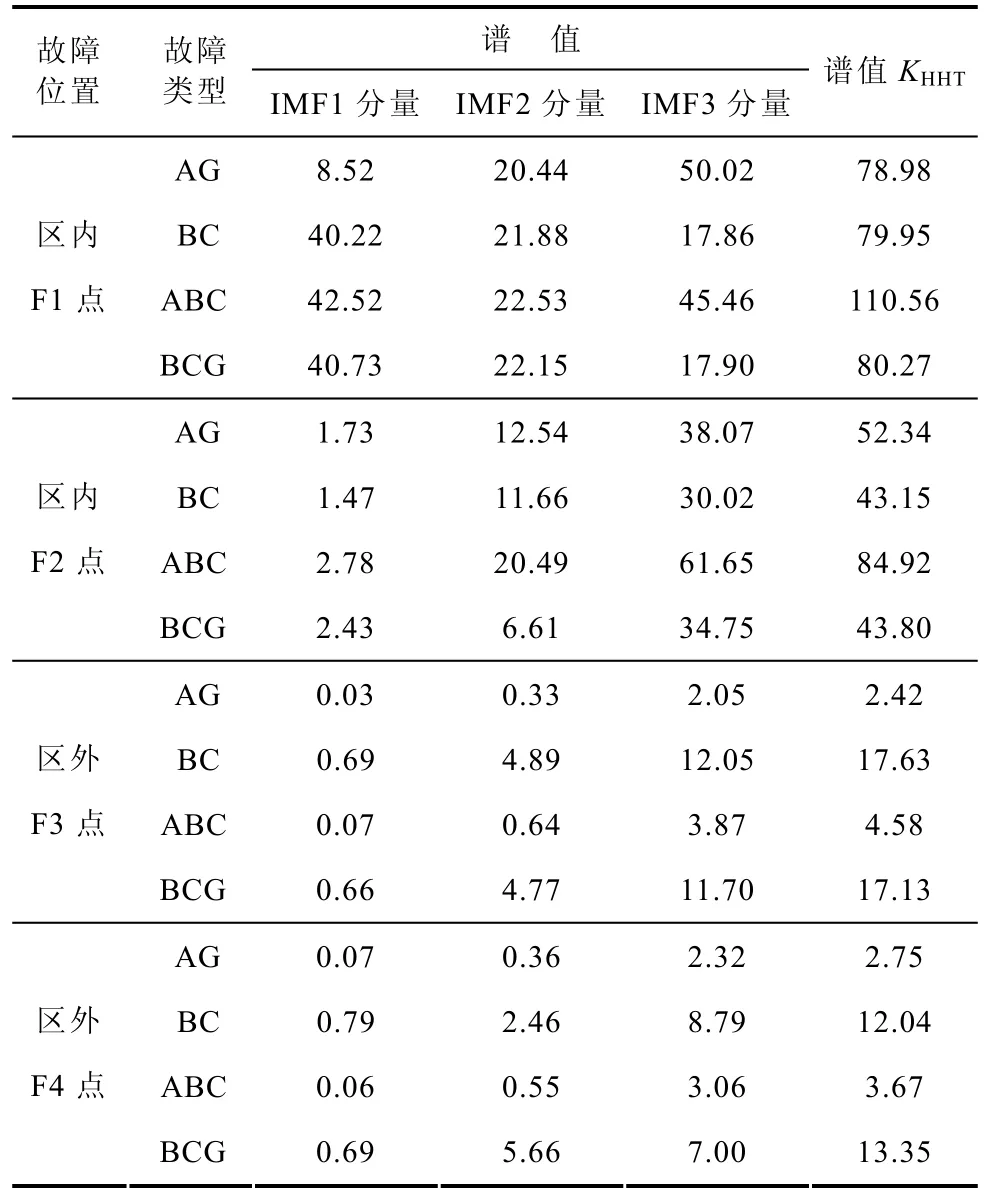
表2 区内外故障时的HHT谱值Tab.2 HHT spectrum value of in-zone and out-zone fault

另外，在仿真过程中，分别采用100kHz、50kHz和20kHz的采样频率进行仿真，仿真结果证明采样频率越高，区内、区外故障时的HHT谱差越明显。但是，采样频率越高，对硬件的要求也越高，难以在实际中得到广泛应用。鉴于采用20kHz的采样频率即可很好地区分出区内和区外故障，所以本文采用20kHz的采样频率，与其他暂态保护的采样频率相比（文献[19]采用 1MHz；文献[20]则采用 200kHz），本文的采样频率大大降低，更有利于硬件的实现。

4 基于HHT谱的STATCOM线路保护新原理

4.1 保护方案

根据区内、外故障时HHT谱特征分析，当并补线路发生故障时，利用区内、外故障时HHT谱值的差异，可以构成判别区内外故障的判据。为了提高保护判据的灵敏度，增加区内外故障时的差异，利用改进HHT方法提取故障发生时刻前三个IMF分量的10个信号点进行叠加，经处理后的保护判据为

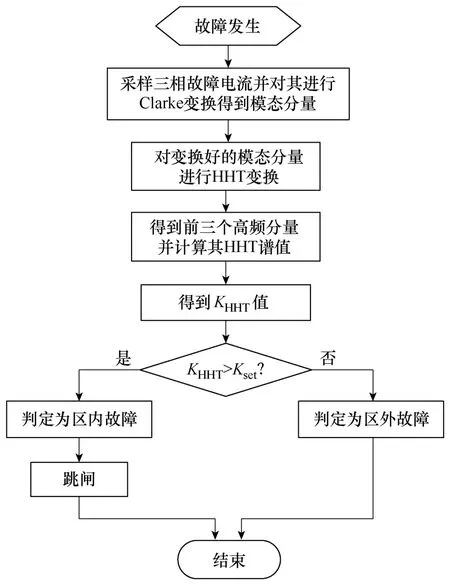
图6 保护方案流程图Fig.6 Flow chart of scheme of STATCOM line protection

4.2 新方案的仿真验证

分别对仿真系统在不同条件下的区内外故障进行了大量的仿真研究，由于篇幅所限，取部分典型结果进行分析说明。其中设定改进算法的时间窗为0.4ms，STATCOM的本体保护的动作时间为9ms，定值取为20。

4.2.1 不同故障类型对保护判据的影响分析

分别对系统中的典型故障位置发生各种故障类型时的HHT谱值进行计算，结果见表2。

对比表2数据可知，不论发生何种故障类型，区内外不同故障点时的HHT谱值均差别明显。区内线路首端发生各种类型的故障时，其HHT谱值均明显高于区外反向出口故障。而且区内线路末端发生各种类型的故障时的 HHT谱值也明显高于区外正向出口故障。因此，保护判据不受故障类型和故障位置的影响，可以有效地区分区内和区外故障。

4.2.2 不同母线电容值对保护判据的影响分析

研究表明，500kV母线系统的对地等效电容值为 6000pF～0.1μF，改变分布电容值分别对线路进行仿真，其结果见表3。

表3 母线不同分布电容时的KHHT值Tab.3 The HHT spectrum values of different capacitance

表3给出了不同母线分布电容时的KHHT值，可以看出，分布电容越大，区外故障信号衰减得越严重，本判据越灵敏。

当分布电容为6000pF时区内、外故障的HHT谱图如图7所示，通过比较表明在最小母线分布电容值6000pF时，区内、外HHT谱值差别依然明显，本判据仍然具有很高的灵敏度，证明本方案不受母线分布电容的影响。

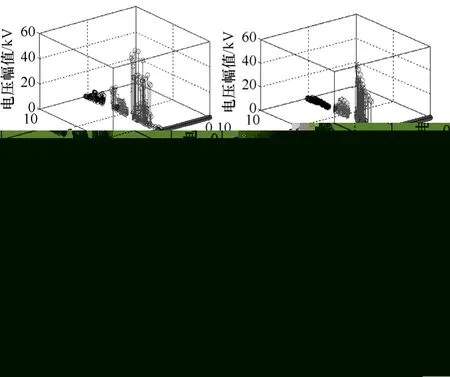
图7 分布电容为6000pF时区内外故障HHT谱图Fig.7 The spectrum chart of in and out zone fault when the capacitance is 6000pF

4.2.3 不同过渡电阻值对保护判据的影响分析

分别对各故障点发生经不同过渡电阻值时的HHT谱值进行分析。由于篇幅所限，只给出过渡电阻为300Ω时的HHT谱图如图8所示，按式（7）计算出的KHHT值见表4。

图8表明在最大过渡电阻为300Ω时，区内和区外故障时的HHT谱值差别均非常明显。由表4可以看出，随着过渡电阻的增大，区内外故障时的KHHT值均减小，但无论过渡电阻大小，本判据均满足灵敏度的要求，且过渡电阻越小，灵敏度越高。

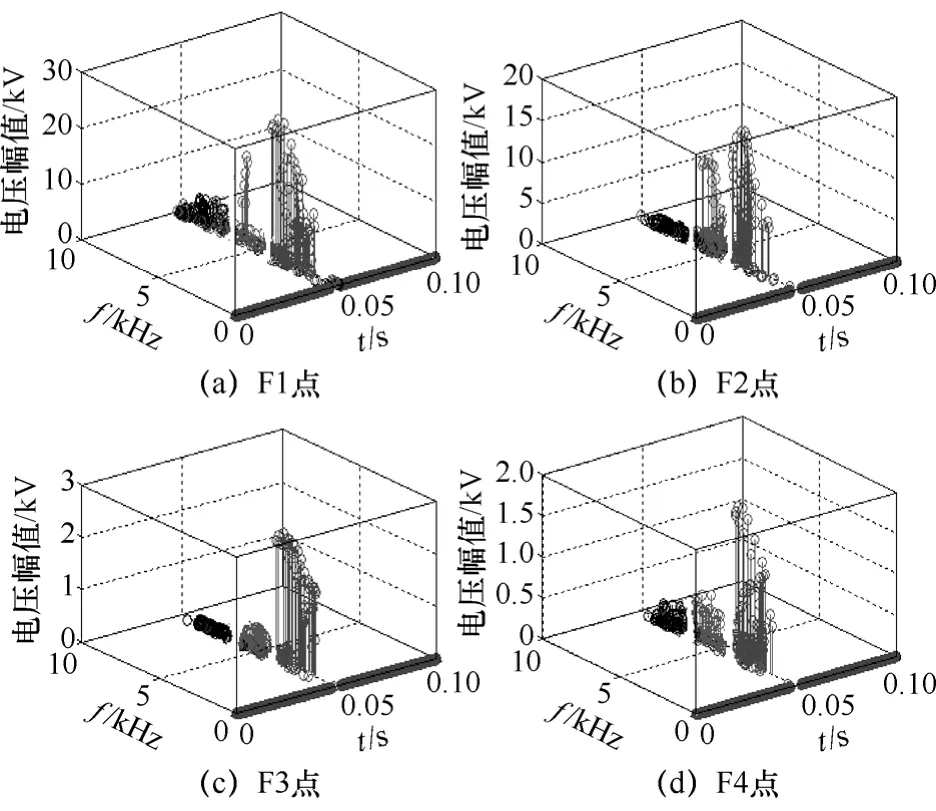
图8 过渡电阻为300Ω时区内外故障谱图Fig.8 The spectrum chart of In and out zone fault when the fault resistance is 300Ω

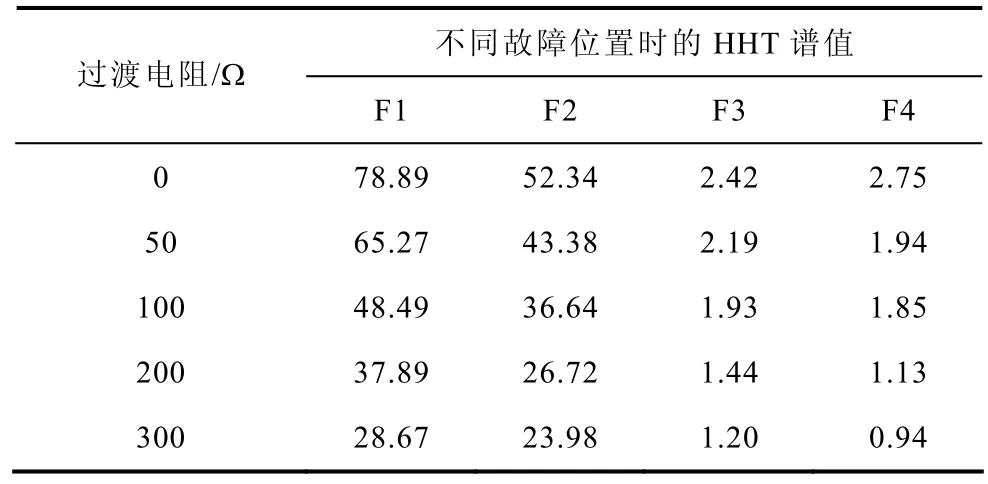
表4 不同过渡电阻下的KHHT值Tab.4 HHT spectrum value of different fault resistance

4.2.4 不同补偿度值对保护判据的影响分析

改变STATCOM的补偿度，分别对各故障位置的谱值进行分析。给出补偿度为零时的HHT谱图如图9所示，不同补偿度时的KHHT值见表5。

表5 不同补偿度下的KHHT值Tab.5 HHT spectrum value of different compensation degrees

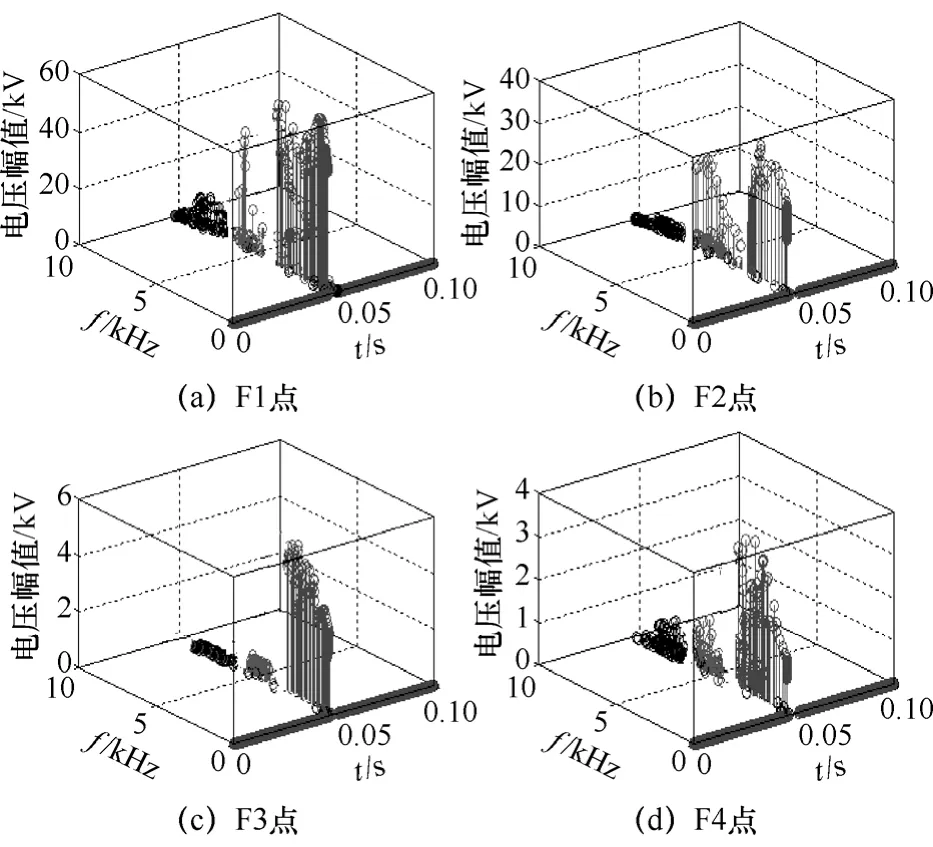
图9 STATCOM补偿度为零时的区内外故障谱图Fig.9 The spectrum chart of In and out zone fault without STATCOM

表5给出了STATCOM在不同补偿度时的KHHT值，可以看到，区内 F1点和 F2点发生故障时的HHT谱值，不论STATCOM补偿度如何变化，均明显高于区外F3点和F4点故障时的谱值，保护判据具有很高的灵敏度。而且在补偿度为零的情况下，保护判据依然能够满足要求，表明本保护方案不受补偿度变化的影响，当STATCOM由于某种原因退出运行时本方案同样适用。

5 结论

通过 PSCAD建模，利用改进 HHT方法对含STATCOM 的并补线路故障电流的 HHT谱特征进行分析。仿真结果证明：

（1）改进HHT方法能适应地提取并补线路中的高频谐波，Hilbert谱能清晰地表示信号能量随时间、频率的分布，有效地消除了原HHT的模态混叠现象。

（2）HHT谱特征分析表明，故障时刻HHT谱会发生突变。且区内故障时的HHT谱值较大，而区外故障时的HHT谱值较小。

（3）根据HHT谱特征构成的并补线路单端暂态保护判据，不受故障类型、过渡电阻、补偿度及母线电容的影响，可以有效地判别区内外故障，具有良好的适应性和灵敏性。

（4）保护判据的算法简单，采样频率较低，随着硬件的快速发展具有较好的应用前景，且本方案对于串补线路的暂态保护具有一定的参考价值。

[1]Dash P K, Pradhan A K, Ganapati Panda, et al.Adaptive relay setting for flexible AC transmission systems (FACTS)[J]. IEEE Transactions on Power Delivery, 2000, 15(1): 38-43.

[2]Tarlochan Singh Sidhu, Rajiv K Varma, Fadhel A Albasri, et al. Performance of distance relays on shunt-FACTS compensated transmission lines[J].IEEE Transactions on Power Delivery, 2005, 20(3):1837-1845.

[3]Xia Y Q, Li K K, David A K. Operation of impedance protection relays with the STATCOM[J]. IEEE Transactions on Power Delivery, 2002, 17(2): 381-387.

[4]Fadhel A Albasri, Tarlochan Singh Sidhu, Rajiv K Varma. Performance comparison of distance protection schemes for shunt-FACTS compensated transmission lines[J]. IEEE Transactions on Power Delivery, 2007,22(4): 2116-2125.

[5]Kazemi A, Jamali S, Shateri H. Effects of STATCOM on distance relay tripping characteristic[C]. Proceedings of the 2005 IEEE/PES Transmission and Distribution Conference & Exhibition: Asia and Pacific, Dalian,China, 2005: 1-6.

[6]Fadhel A Albasri, Sidhu T S, Rajiv K Varma.Mitigation of adverse effects of midpoint shunt-FACTS compensated transmission lines on distance protection schemes[C]. Proceedings of the IEEE Power Engineering Society General Meeting, 2007:1-8.

[7]吴振杰. STATCOM对距离保护影响的研究[D]. 北京: 华北电力大学, 2003.

[8]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the hilbert spectrum for non linear and non-stationary time series analysis1[J].Proceedings of the Royal Society of London, A, 1998:903-995.

[9]王波, 杨洪耕. 电力系统电压短期扰动的三角模态检测方法[J]. 电工技术学报, 2005, 20(11): 101-105.Wang Bo, Yang Honggeng. Triangle mode method for detection of short-term voltage disturbance of power system[J]. Transactions of China Electrotechnical Society, 2005, 20(11): 101-105.

[10]熊卫华, 赵光宙. 基于希尔伯特-黄变换的变压器铁心振动特性分析[J]. 电工技术学报, 2006, 21(8):9-13.Xiong Weihua, Zhao Guangzhou. Analysis of transformer core vibration characteristics using Hilbert-Huang transformation[J]. Transactions of China Electrotechnical Society, 2006, 21(8): 9-13.

[11]刘毅华, 赵光宙. 希尔伯特-黄变换在电力系统故障检测中的应用研究[J]. 继电器, 2006, 34(14): 4-6,19.Liu Yihua, Zhao Guangzhou. Application of Hilbert-Huang transform in power system fault detection[J].Relay, 2006, 34(14): 4-6, 19.

[12]李天云, 赵妍, 季小慧, 等. HHT方法在电力系统故障信号分析中的应用[J]. 电工技术学报, 2005,20(6): 87-91.Li Tianyun, Zhao Yan, Ji Xiaohui, et al. Application of HHT method for analysis of fault signal in electric power system[J]. Transactions of China Electrotechnical Society, 2005, 20(6): 87-91.

[13]向玲, 朱永利, 唐贵基. HHT方法在转子振动故障诊断中的应用[J]. 中国电机工程学报, 2007, 27(35):84-89.Xiang Ling, Zhu Yongli, Tang Guiji. Application of Hilbert-Huang transform method in vibration faults diagnosis for rotor system[J]. Proceedings of the CSEE, 2007, 27(35): 84-89.

[14]李天云, 程思勇, 杨梅. 基于希尔伯特-黄变换的电力系统谐波分析[J]. 中国电机工程学报, 2008,28(4): 109-113.Li Tianyun, Cheng Siyong, Yang Mei. Power system harmonic analysis based on Hilbert-Huang transform[J]. Proceedings of the CSEE, 2008, 28(4):109-113.

[15]赵庆明, 贺家李, 李永丽. 基于希尔伯特-黄变换的超高速方向保护研究[J]. 电网技术, 2007, 31(10):79-83.Zhao Qingming, He Jiali, Li Yongli. Study of ultra-high-speed directional protection of transmission lines based on Hilbert-Huang transform[J]. Power System Technology, 2007, 31(10): 79-83.

[16]李天云, 赵妍, 李楠, 等. 基于 HHT的电能质量检测新方法[J]. 中国电机工程学报, 2005, 25(17):52-56.Li Tianyun, Zhao Yan, Li Nan, et al.A new method for power quality detection based on HHT[J].Proceedings of the CSEE, 2005, 25(17): 52-56.

[17]段建东, 张保会, 任晋峰, 等. 超高压输电线路单端暂态量保护元件的频率特性分析[J]. 中国电机工程学报, 2007, 27(1): 37-43.Duan Jiandong, Zhang Baohui, Ren Jinfeng, et al.Single-ended transient-based protection for EHV transmission lines basic theory[J]. Proceedings of the CSEE, 2007, 27(1): 37-43.

[18]李向荣, 罗承廉, 李勇, 等. STATCOM应用于2000年华中电网的仿真研究[J]. 电力系统自动化, 2000,24(23): 6-9.Li Xiangrong, Luo Chenglian, Li Yong, et al.Simulation of the STATCOM in central china power system in 2000[J]. Automation of Electric Power Systems, 2000, 24(23): 6-9.

[19]马静, 王增平. 基于小波-形态学的串补线路超高速保护新方法[J]. 电网技术, 2006, 30(11): 77-80.Ma Jing, Wang Zengping. A novel method of ultra-high speed protection for series compensated lines based on wavelet-morphology[J]. Power System Technology, 2006, 30(11): 77-80.

[20]胡巨, 杨明玉. 利用暂态电流的高压输电线路暂态保护新方案[J]. 继电器, 2005, 33(1): 21-23.Hu Ju, Yang Mingyu. A novel scheme of non-unit protection for EHV transmission line based on transient components[J]. Relay, 2005, 33(1): 21-23.