恒定导通时间双频率控制开关变换器
王金平 许建平 兰燕妮
(西南交通大学电气工程学院 成都 610031)
1 引言
开关变换器因其具有高功率转换效率和高功率密度等明显优点而逐步取代传统线性稳压电源,在工业界获得越来越广泛的应用。开关变换器的瞬态特性和控制鲁棒性,以及由于开关功率器件的高速导通与关断所产生的电压瞬变 dv/dt和电流瞬变di/dt而带来的电磁干扰[1-3],是学术界和工业界关注的重要问题。
开关变换器 EMI与其电路拓扑及其控制方法密切相关。采用软开关技术可以有效抑制开关变换器的 EMI,但却存在设计和实现困难的问题[4]。因此,人们研究了多种改善开关变换器EMI特性的控制策略[5-8]。
开关变换器是强非线性系统,基于传统线性反馈控制的 PWM开关变换器很难获得满意的瞬态特性和鲁棒性控制效果。针对传统线性反馈控制存在的问题,人们提出并研究了开关变换器的单周控制[9]、滑模控制[10]、滞环控制[11-12]等非线性控制方法。单周控制原理简单,对输入电压的扰动具有较强的抑制能力,但系统存在稳态误差且对负载扰动抑制能力较差;滑模控制能够改善开关变换器的瞬态响应速度,但控制策略比较复杂;滞环控制的开关频率随着输入电压或负载的变化而波动,难以优化反馈控制环路及EMI滤波器的设计。
为了改善开关电源的瞬态特性和控制鲁棒性,以及降低开关电源的EMI,本文提出了一种新颖的开关变换器控制技术,恒定导通时间双频率(Constant On-Time Bi-Frequency, COT-BF)控制技术。COT-BF控制电路简单,无需误差放大器及其相应的补偿网络,具有比传统 PWM开关变换器更快的瞬态响应速度和更低的电磁干扰。本文以DCM Buck变换器为例,分析了COT-BF控制开关变换器的工作原理及控制策略。实验研究结果验证了理论分析的正确性和COT-BF控制性能的优越性。
2 COT-BF控制技术
如图 1所示为 COT-BF控制 Buck变换器,其中COT-BF控制器由逻辑控制电路、采样/保持电路、比较器和驱动电路构成。逻辑控制电路在每一个控制脉冲周期结束时刻产生采样时钟信号clk,使采样/保持电路采样输出电压,当输出电压采样值小于参考电压 Vref时,比较器输出高电平,控制器选择高频率控制脉冲PH;否则,比较器输出低电平,控制器选择低频率控制脉冲PL。
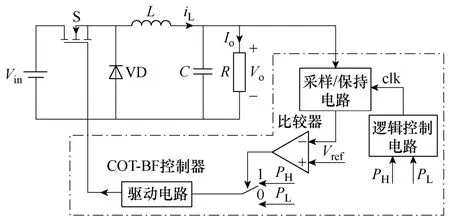
图1 COT-BF控制Buck变换器Fig.1 COT-BF controlled Buck converter
图2所示为COT-BF控制DCM Buck变换器的工作波形,从图中可以看出,高频率控制脉冲 PH和低频率控制脉冲PL具有相同的导通时间 tON,不同的开关周期TH和TL(k=TL/TH,k>1)。当控制器选择 PH时,Buck变换器输入功率大于输出功率,多余的能量全部储存在电容中,输出电压上升;反之,当控制器选用 PL时,Buck变换器输入功率小于输出功率,电容释放能量,输出电压下降。
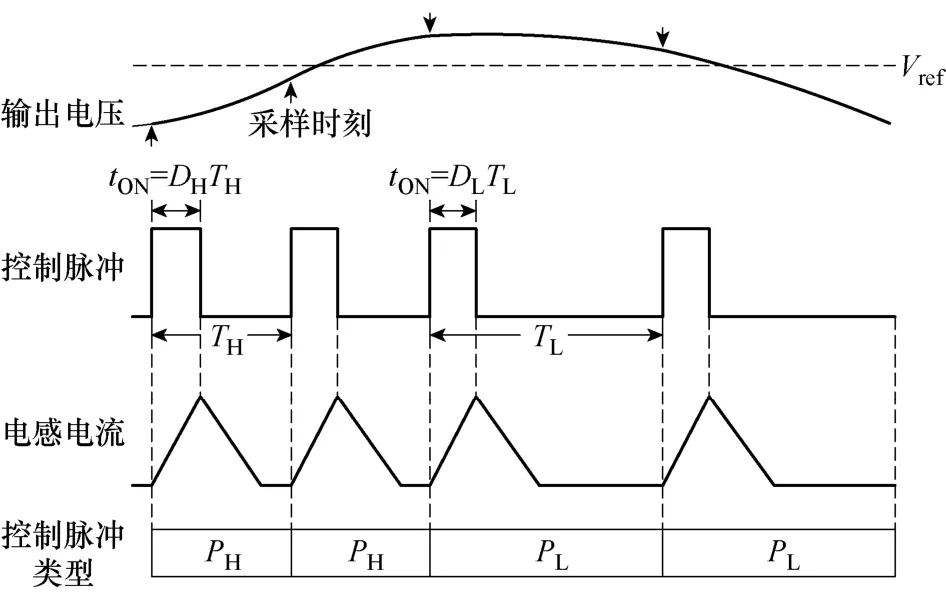
图2 COT-BF控制的工作波形Fig.2 Operation waveforms of COT-BF control
当开关变换器工作于稳态时,若干高频率控制脉冲 PH和低频率控制脉冲 PL形成一个循环周期,COT-BF控制技术通过调整一个循环周期内高频率控制脉冲 PH和低频率控制脉冲 PL的组合,实现COT-BF控制开关变换器输出电压的调整。
由此不难看出COT-BF与PWM是两种完全不同的控制技术: PWM控制是通过对每个开关周期控制脉冲占空比进行连续调节,实现开关变换器输出电压的调整,具有稳态精度高、但瞬态响应速度慢的特点;COT-BF控制是通过选择事先设定好的高、低频率控制脉冲,实现输出电压的调节,它具有瞬态响应速度快、但稳态精度较低的特点。
当分别采用高频率控制脉冲 PH和低频率控制脉冲PL时,DCM Buck变换器输入功率Pin,H、Pin,L分别为
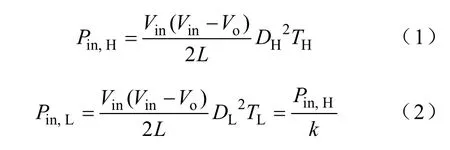
从式(1)和式(2)可以看出,采用高频率控制脉冲PH时,输入端将提供较多的输入功率;采用低频率控制脉冲PL时,输入端将提供较少的输入功率。因此,当输出功率越大时,COT-BF控制器将选用更多的高频率控制脉冲PH。
COT-BF工作的极端情形为控制器一直选用PH或PL,因而COT-BF控制Buck变换器稳定工作时的输出功率Po需满足
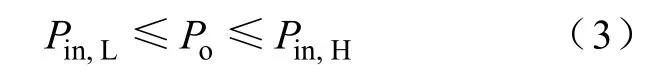
由式(3)可知,在给定功率范围内,不论负载如何变化,高、低频率控制脉冲提供的输入功率总是大于、小于负载功率。因此当负载突变时,控制器将立即采用高频率控制脉冲(加载)或低频率控制脉冲(减载)工作,从而在变换器输入端提供大于(加载)或小于(减载)负载功率的输入功率,因而能够迅速调整变换器输出电压,使变换器快速进入稳态。由此可知,COT-BF控制具有快速的负载瞬态响应速度。
另外,开关变换器 EMI研究成果表明,PWM开关变换器 EMI峰值主要集中在开关频率及其倍频处[7]。本文研究的 COT-BF控制开关变换器,是通过调整PH、PL的组合实现开关变换器输出电压的调节,因此,COT-BF控制开关变换器的开关频率不再单一、恒定,COT-BF控制开关变换器的 EMI与高、低频率控制脉冲的周期以及循环周期紧密相关,控制脉冲频谱能量被扩展到更宽的频带范围,从而有效降低了EMI峰值,使开关变换器具有更低的 EMI。
3 控制脉冲组合分析
3.1 输出电压变化量分析
图3所示为DCM Buck变换器在一个控制脉冲周期内的电感电流及输出电压波形,DCM Buck变换器的一个控制脉冲周期可以分为tON、tF、tB三个阶段。在 tON阶段,开关管导通,二极管截止,电感电流线性上升;在tF阶段,开关管关断,二极管续流,电感电流线性下降;在tB阶段,开关管关断,二极管截止,电感电流为零。对于 Buck变换器,当电感电流iL大于负载电流Io时(tAB),电容充电,输出电压上升;反之,电容放电,输出电压下降。
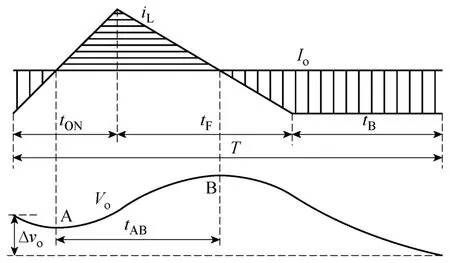
图3 一个控制脉冲周期内的电感电流及输出电压Fig.3 Inductive current and output voltage in a control pulse
由于DCM Buck变换器电感电流在任意控制脉冲周期开始及结束时刻均为零,输出电容的等效串联电阻(Equivalent Series Resistance, ESR)不影响控制脉冲周期内输出电压的变化量。因此,DCM Buck变换器在一个控制脉冲周期内输出电压的变化量ovΔ满足:
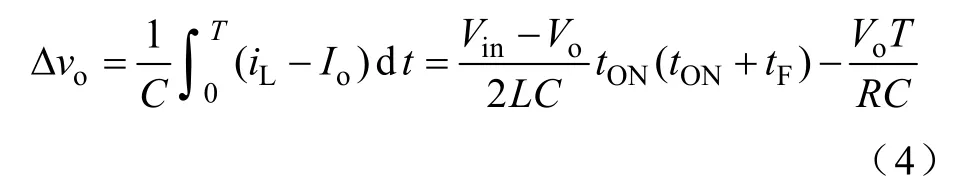
当采用高频率控制脉冲PH时,有
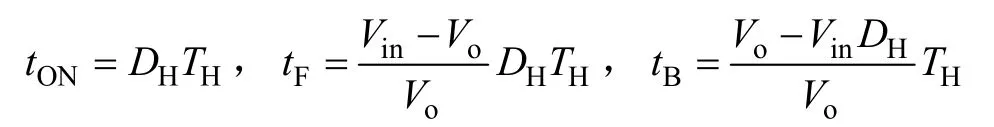
由式(4)可得一个高频率控制脉冲周期内输出电压的变化量为
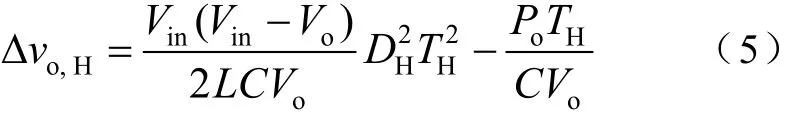
当COT-BF控制器选用高频率控制脉冲PH时,输出电压上升,即≥ 0,因此可得
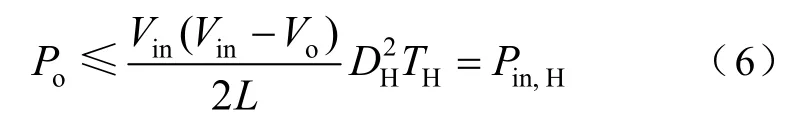
式(6)确定了 COT-BF控制DCM Buck变换器的最大输出功率。
从式(5)和式(6)可知,当控制脉冲PH的占空比 DH增大时,输出功率范围随之增加,但同时导致输出电压变化量的增加。
当采用表1所示电路参数时,得到如图4所示高频率控制脉冲周期内输出电压变化量与占空比DH、输出功率 Po之间的关系。从图 4可以看出,占空比越大时,输出功率范围越大,且输出电压变化量也越大,DH=0.2和DH=0.4对应的最大输出功率分别为 2W 和 8W;对于同一个占空比,输出电压变化量随着输出功率的增加而变小;随着输出功率的进一步增加,输出电压变化量由正变负,输出电压下降,输出电压将低于期望输出电压,控制失效。因此,在设计COT-BF控制DCM Buck变换器时,应满足式(6)的条件。

表1 电路参数Tab.1 Circuit parameters
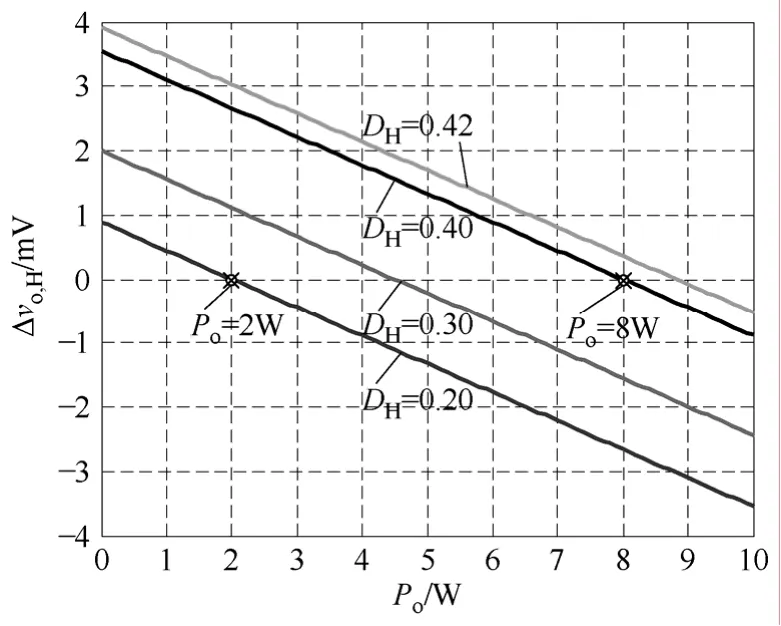
图4 不同占空比时输出电压变化量与输出功率间的关系Fig.4 Output voltage variation as a function of output power for different duty ratios
同理,可得输出电压在一个低频率控制脉冲周期内的输出电压变化量为
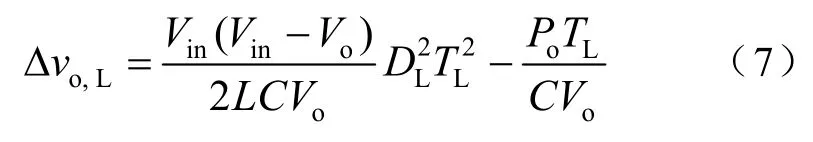
当选用PL时,输出电压下降,即Δvo,L≤0,从而有
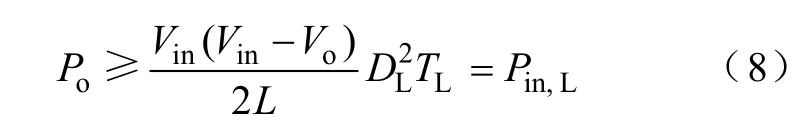
式(8)确定了COT-BF控制DCM Buck变换器的最小输出功率。
同样,在设计COT-BF控制DCM Buck变换器时,应满足式(8)的条件。
3.2 控制脉冲组合分析
假定COT-BF控制DCM Buck变换器稳态工作时,一个循环周期有μH个PH脉冲和μL个PL脉冲,由于稳态时一个循环周期内输出电压变化量为零,因而有
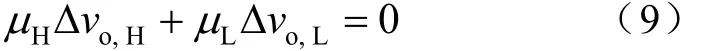
将式(1)、式(2)、式(5)和式(7)代入式(9)可得
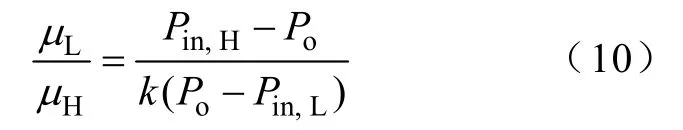
式(10)给出了一个循环周期内 PH脉冲数和PL脉冲数的比值μL/μH与输出功率Po的关系。
图5为采用表1所示电路参数时,μL/μH与输出功率Po关系图。由图5可知,随着输出功率的增加,μL/μH比值变小,循环周期内 PH脉冲的比重增加;当输出功率为8W时,μL/μH比值为零,即控制器仅选用PH工作。
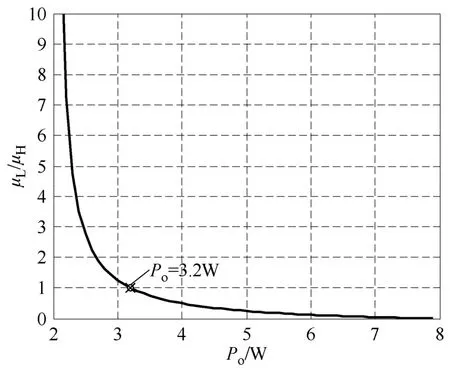
图5 μL/μH与输出功率关系Fig.5 μL/μH as a function of output power
表2给出了循环周期内PH、PL的组合。从表中同样可以看出,随着输出功率的增加,μL/μH比值明显减小,PH比重增加,控制器选用更多的 PH,以向负载端传递所需的能量。
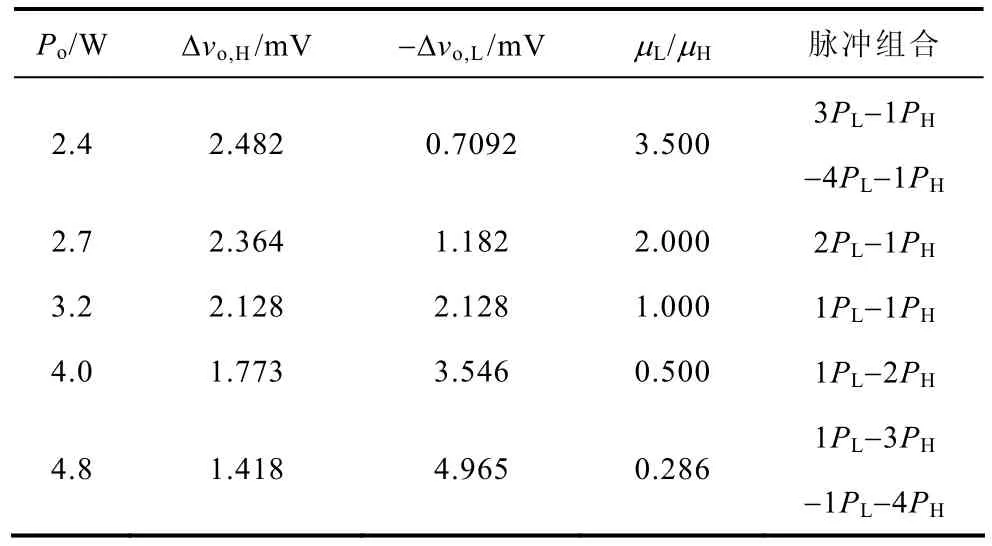
表2 循环周期内控制脉冲组合Tab.2 Combination of control pulses in a repetition cycle
3.3 开关变换器效率η 对控制脉冲组合影响
上面的分析是基于开关变换器效率η =100%的前提下得出的。在实际中,开关变换器效率η 总是小于100%,因此,有必要研究效率η 对COT-BF控制开关变换器控制脉冲组合的影响。
假定COT-BF控制DCM Buck变换器稳态工作时,一个循环周期有μH个PH脉冲和μL个PL脉冲,则输入功率与输出功率之间存在如下关系
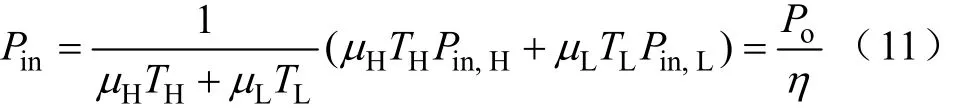
由式(11)可以进一步得到
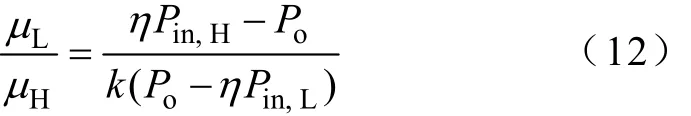
当η =100%时,式(12)与式(10)相同。
图6为采用表1所示电路参数时,开关变换器效率η 对μL/μH的影响。从图6可以看出,效率对控制脉冲的组合有着重要影响,随着效率的降低,μL/μH变小,PH脉冲数量明显增加。表 3给出了不同开关变换器效率时循环周期内控制脉冲的组合。
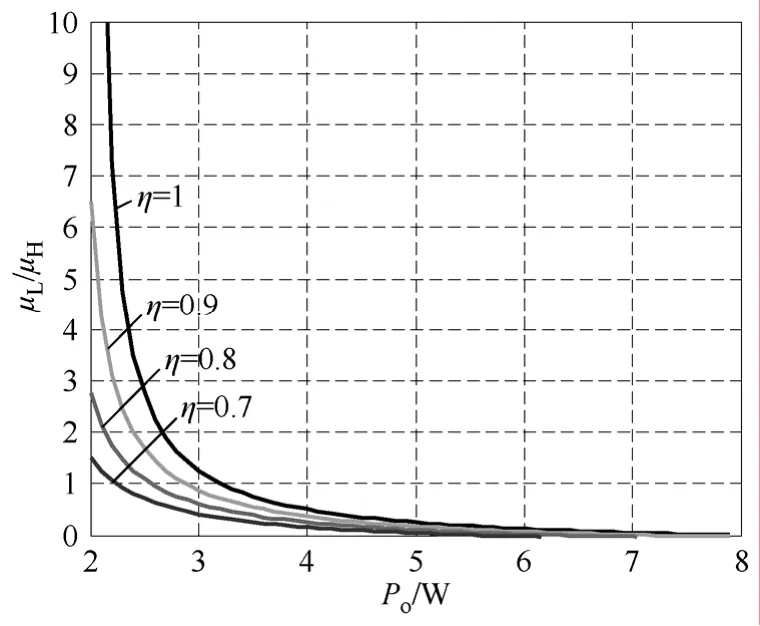
图6 开关变换器效率η 对控制脉冲组合的影响Fig.6 The effect of power conversion efficiency η on the combination of control pulses
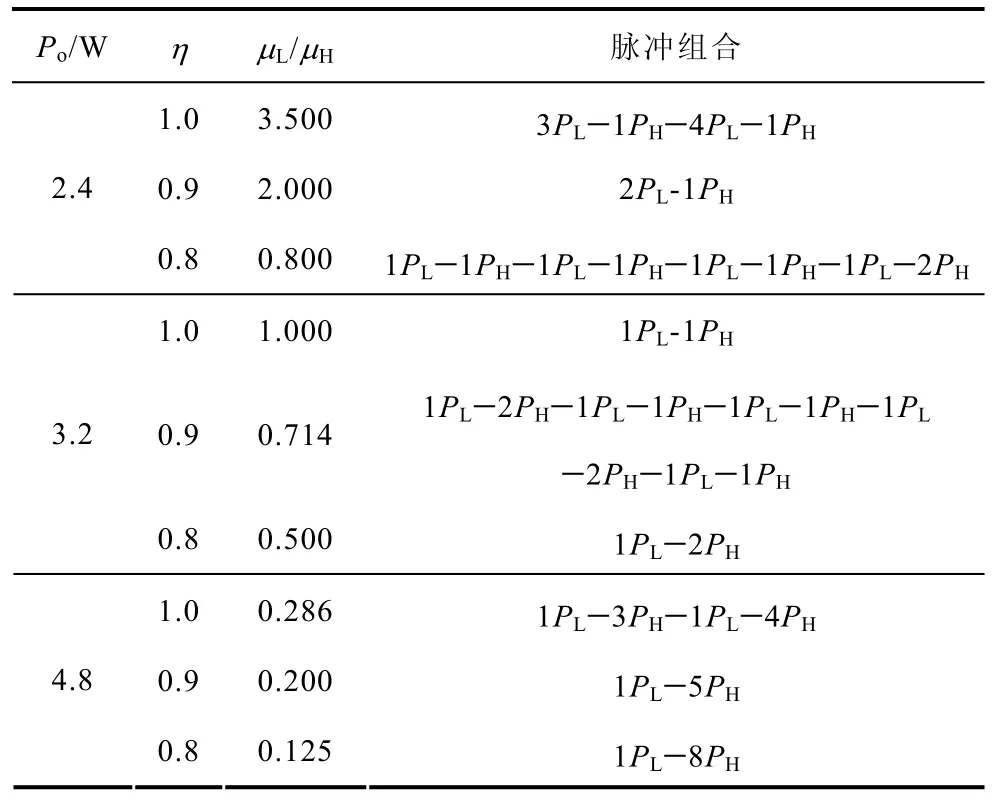
表3 不同功率变换效率时控制脉冲组合Tab.3 Combination of control pulses under different power conversion efficiencies
4 实验验证
为了验证理论分析的正确性,采用表1所示电路参数,搭建了相应的实验平台进行实验验证,其中COT-BF控制环路采用基于FPGA的数字实现方式,模数转换器采用LTC2366。实验系统工作过程如下:在任意控制脉冲周期的结束时刻,模数转换器采样输出电压,FPGA根据采样时刻输出电压与参考电压间的大小关系,相应地生成高或低频率控制脉冲对输出电压进行调整;在控制脉冲周期结束时刻,FPGA再次使能模数转换器采样输出电压,依此循环。
图 7a、图 7b分别为 COT-BF控制 DCM Buck变换器输出功率为 3.2W 与 4.8W 时的稳态实验结果。从图7a可以看出,循环周期由5PL和6PH组成,此时 0.714<μL/μH=0.833 < 1.000。由表 3 可知,μL/μH=0.714与μL/μH=1.000分别对应功率变换效率为90%与100%时输出3.2W功率的结果。由此可以预测开关变换器的效率大于90%。根据脉冲组合关系,由式(1)、式(2)及式(12)可得变换器的效率η =94.5%,与实际测量值 94.3%非常相近。在图7b中,循环周期由1PL和5PH组成,类似地,可以预测系统转换效率为90%,与实际测量值89.6%非常接近。
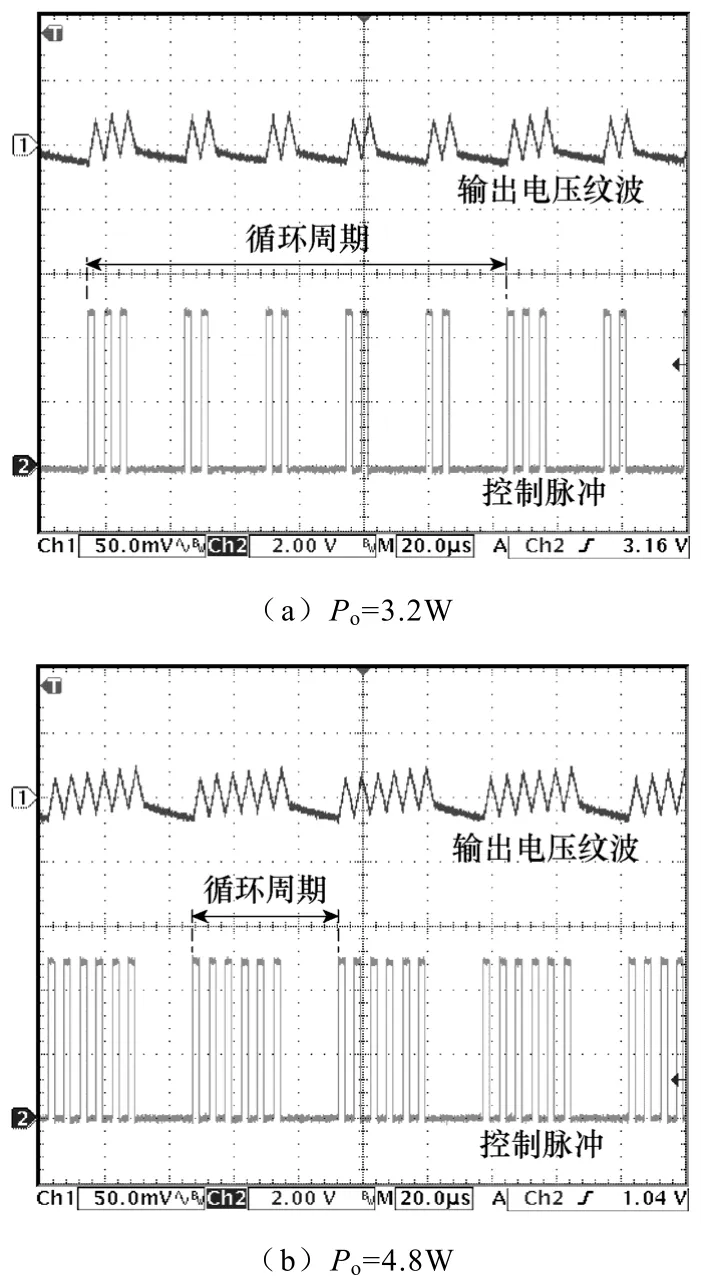
图7 稳态实验结果Fig.7 Experimental results of steady-state
此外,比较图7a和图7b可以发现,随着输出功率的增加,循环周期内 PH所占的比重也相应增加。
图8为负载电流由0.4A突变至0.8A时,PWM与COT-BF控制Buck变换器瞬态响应速度对比图。对于PWM控制,分别给出了开关周期为TS=5µs和TS=20µs的实验结果;而对于 COT-BF控制,高、低频率控制脉冲的开关周期分别为 TH=5µs和TL=20µs。从图8可以看出,当负载突变时,COT-BF控制 Buck变换器几乎无电压跌落及超调,具有快速的瞬态响应速度,从而能够更好地抑制由负载变化引起的输出电压波动。
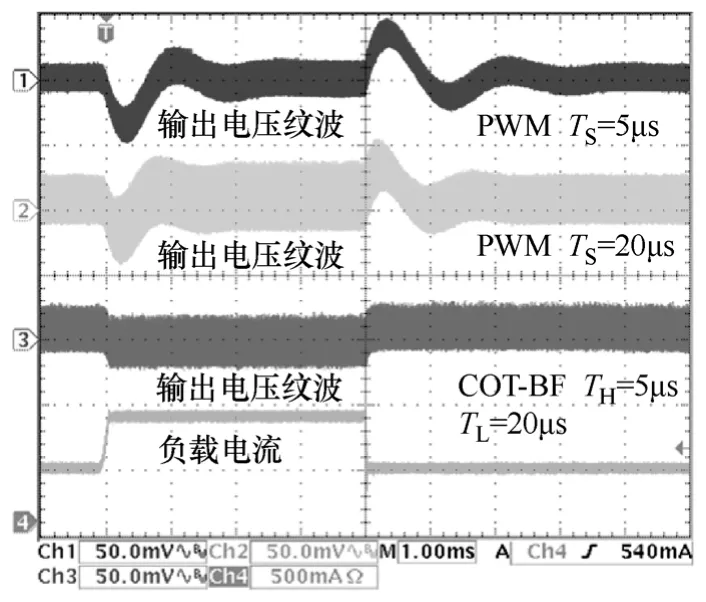
图8 负载瞬态响应速度对比Fig.8 Comparison of load transient response
图9为图8中COT-BF控制Buck变换器负载由2.4W突变至4.8W时的局部放大图。负载突变后,控制脉冲循环周期组成由3PL-1PH变为1PL-5PH,而由图7b可知,1PL-5PH恰好是输出功率为4.8W时循环周期的脉冲组成。因此,从图9可知,当负载突变时,COT-BF控制Buck变换器仅仅经过一个PH周期的调整时间便立即进入新的稳态。由此可以看出,COT-BF控制在瞬态响应速度方面的优越性。
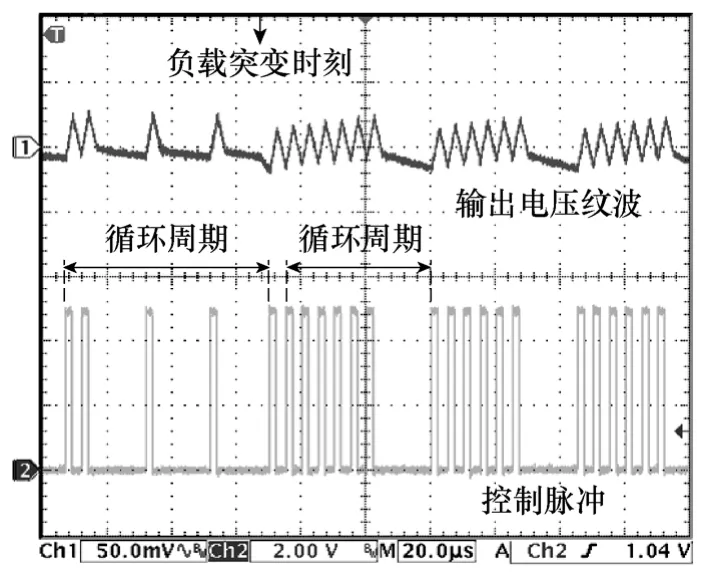
图9 负载瞬态响应实验结果Fig.9 Experimental results of load transient response
图10为PWM与COT-BF控制Buck变换器功率MOSFET漏源间电压VDS的频谱图。从图中可以看出,当采用 COT-BF控制时,VDS频谱具有最低的谐波峰值,由此可以看出COT-BF控制技术在抑制开关变换器EMI方面的优越性。
5 结论
本文提出了开关变换器的恒定导通时间双频率控制技术,并以 DCM Buck变换器为例,分析了COT-BF控制原理和控制策略,着重研究了循环周期内控制脉冲的组成,并考虑了开关变换器效率的影响。COT-BF控制技术实现简单、可靠,无需误差放大器及其相应的补偿网络。相应的实验结果表明,COT-BF控制DCM Buck具有快速的瞬态响应速度和较低的电磁干扰噪声,从而使得开关变换器具有更优的性能。
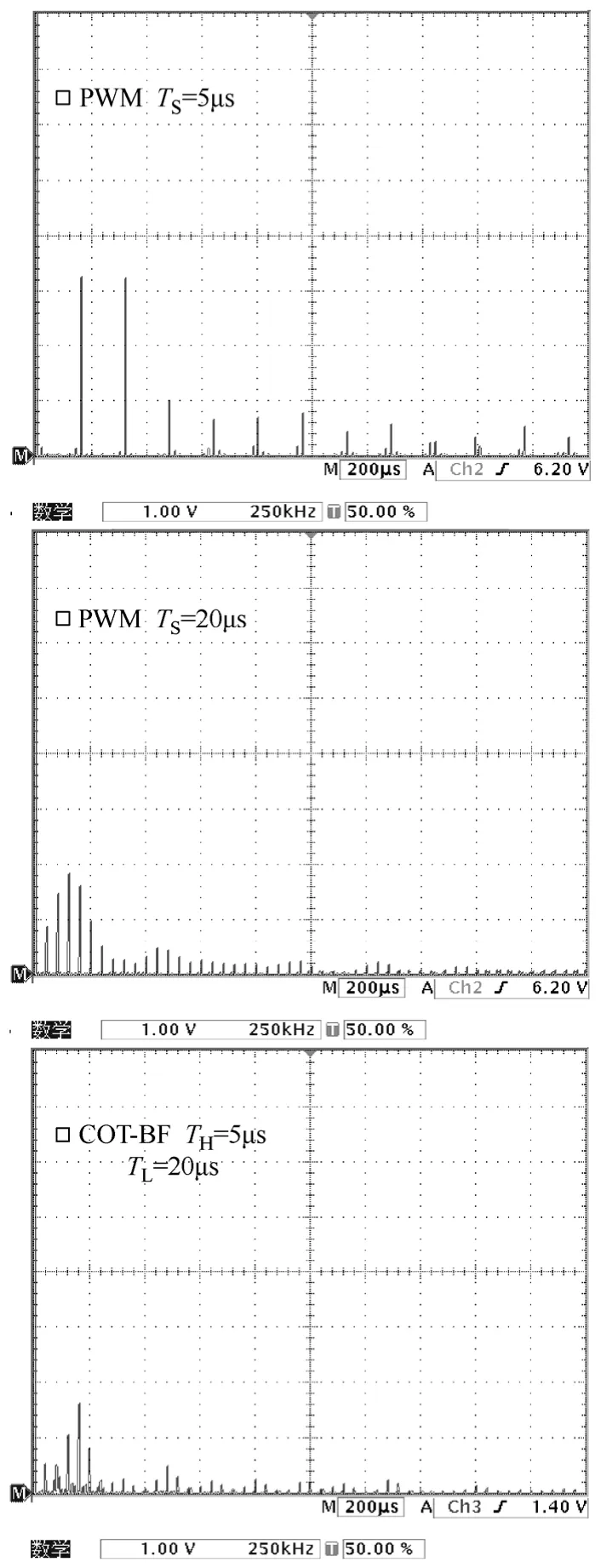
图10 VDS频谱对比Fig.10 Comparison of spectra of VDS
本文仅研究了COT-BF控制技术在DCM Buck变换器中的应用,COT-BF可以类似的应用于其他DCM 开关变换器。但电感电流连续导电模式(CCM)开关变换器的 COT-BF控制特性与 DCM开关变换器的COT-BF控制特性有较大区别,有关COT-BF控制CCM开关变换器的控制特性还有待进一步深入研究。
[1]钱照明, 陈恒林. 电力电子装置电磁兼容研究最新进展[J]. 电工技术学报, 2007, 22(7): 1-11.Qian Zhaoming, Chen Henglin. State of art of electromagnetic compatibility research on power electronic equipment[J]. Transactions of China Electrotechnical Society, 2007, 22(7): 1-11.
[2]Costa F, Magnon D. Graphical analysis of the spectra of EMI sources in power electronics[J]. IEEE Transactions on Power Electronics, 2005, 20(6):1491-1498.
[3]吴振军, 胡智宏, 崔光照. 基于混沌反控制降低Buck型变换器EMI及纹波研究[J]. 系统仿真学报,2008, 20(4): 993-996.Wu Zhenjun, Hu Zhihong, Cui Guangzhao. Research on reducing EMI and output voltage ripple of Buck converter based on anti-control of choas[J]. Journal of System Simulation, 2008, 20(4): 993-996.
[4]Chung H, Hui S Y R, Tse K K. Reduction of power converter EMI emission using soft-switching technique[J]. IEEE Transactions on Electromagnetic Compatibility, 1998, 40(3): 282-287.
[5]李志忠, 丘水生, 陈艳峰. 混沌调制对开关变换器EMI抑制有效性的实验研究[J]. 电工技术学报,2006, 21(8): 97-102.Li Zhizhong, Qiu Shuisheng, Chen Yanfeng.Experimental study on the effectiveness of EMI suppression with chaotic modulation for switching converters[J]. Transactions of China Electrotechnical Society, 2006, 21(8): 97-102.
[6]Tse K K, Chung H, Hui S Y R, et al. A comparative study of carrier-frequency modulation techniques for conducted EMI suppression in PWM converters[J].IEEE Transactions on Industrial Electronics, 2002,49(3): 618-627.
[7]杨汝, 张波, 丘东元. 混沌开关变换器 EMI动态频谱的小波分析[J]. 电工技术学报, 2007, 22(11):110-116.Yang Ru, Zhang Bo, Qiu Dongyuan. Wavelet analysis of dynamic EMI spectrum in chaotic switching-mode converter[J]. Transactions of China Electrotechnical Society, 2007, 22(11): 110-116.
[8]Barragán L A, Navarro D, Acero J, et al. FPGA implementation of a switching frequency modulation circuit for EMI reduction in resonant inverters for induction heating appliances[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 11-20.
[9]Smedley K M, Ćuk S. One-cycle control of switching converters[J]. IEEE Transactions on Power Electronics, 1995, 10(6): 625-633.
[10]Tan S C, Lai Y M, Tse C K. General design issues of sliding mode controllers in DC-DC converters[J].IEEE Transactions on Industrial Electronics, 2008,55(3): 1160-1174.
[11]Castilla M, Vicuna L G de, Guerrero J M, et al.Designing VRM hysteretic controllers for optimal transient response[J]. IEEE Transactions on Industrial Electronics, 2007, 54(3): 1726-1738.
[12]Castilla M, Vicuna L G de, Guerrero J M, et al.Simple low-cost hysteretic controller for single-phase synchronous buck converters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1232-1241.

