基于频域建模与遗传算法的电力电子电路参数辨识方法

孙凤艳 王友仁 林 华 崔 江 姜媛媛

（南京航空航天大学自动化学院 南京 210016）

1 引言

随着航空与航天事业的不断发展，航空航天飞行器的安全性和可靠性要求日益提高，由此飞机健康预报与管理技术得到越来越多的关注[1-2]。电力电子电路是飞机二次电源系统的重要组成部分[3]，对电力电子电路故障诊断和故障预测技术的研究具有重要意义与应用前景。

电力电子电路故障分为结构型故障和参数型故障。目前，电力电子电路故障诊断技术的研究多数采用智能诊断方法，如支持向量机[4]、模糊推理[5]和神经网络等[6-9]，这类方法需要预先划分元器件参数偏差等级来设置故障模式，利用不同故障模式下的样本数据来训练分类器，由此实现故障诊断。当元器件参数偏差较小时，由于元器件容差的存在，会导致故障诊断正确率很低，甚至难以进行故障诊断。为了有效诊断电力电子电路参数型故障，出现了基于参数辨识的电力电子电路故障诊断方法[10-12]。通过参数辨识能准确获知电路中故障元器件参数值，从而实现参数型故障诊断，这种方法一般需要建立电路数学模型，且参数估计方法直接决定了参数辨识的准确性。

面向电力电子电路参数型故障诊断，研究一种电力电子电路参数辨识新方法。本文建立了电路频域传递函数模型，给出了基于傅里叶变换的频域特性求解方法，利用遗传算法进行电力电子电路参数辨识，以Buck电路为例，验证了该方法的有效性。

2 电力电子电路参数辨识方法

2.1 频域传递函数模型

针对电力电子电路参数辨识，必须建立其电路数学模型。对于不同的电路，应根据电路的功能和结构特点，确定反映电路工作过程的频域模型。

Buck电路是电力电子电路中实现降压转换的电路，是电力电子电路中最基本的电路。以图1所示的 Buck电路为例，分析电力电子电路频域传递函数模型的建立过程。

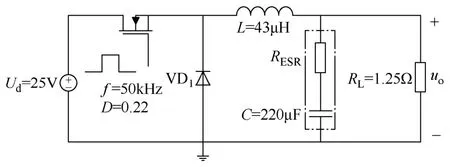
图1 Buck电路图Fig.1 Circuit diagram of Buck converter

图1中，开关MOSFET为IRF151，其开关频率 f =50kHz，占空比D=0.22；滤波电感L为43μH，VD1为续流二极管；输出滤波电容C为220μF，此处采用理想电容C和等效串联电阻RESR来表示实际电容；负载性质为阻性负载1.25Ω。

通过电路分析可知，开关管导通、截止及二极管的截止与导通对于电感、电容器及负载支路来讲，电路的拓扑结构并没有发生改变。Buck电路工作在连续工作方式，当开关管导通、二极管截止时，电感输入端电压值为直流输入电压与开关导通压降之差；当开关管截止、二极管导通时，电感输入电压值为二极管正向导通压降。在开关管和二极管为理想器件情况下，该电感输入端电压信号可以等效为一个脉冲波形uin。其高电平等于输入直流电压、低电平为零。此时 Buck电路的拓扑结构等效电路如图2所示。

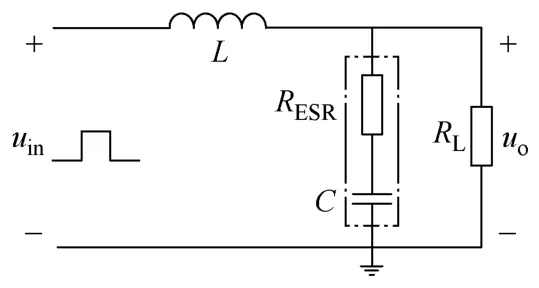
图2 MOSFET开关之后等效电路图Fig.2 Equivalent circuit of Buck converter

根据频域传递函数定义，图2所示电路的传递函数H(s)为

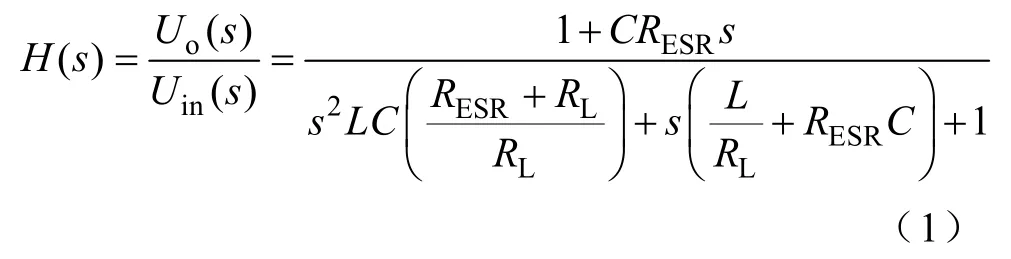
式中 Uin(s)—电感输入端脉冲电压 uin的拉普拉斯变换；

Uo(s)—输出电压uo的拉普拉斯变换。

将s=jω代入式（1），可得

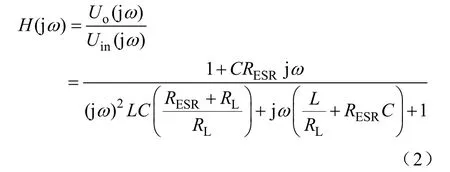
式中 Uin(jω)—电感输入端脉冲电压 uin的傅里叶变换；

Uo(jω)—输出电压uo的傅里叶变换；

H(jω)—电路频域特性。

2.2 频域特性求解

对于电力电子电路频域特性或频域模型参数的求解，可通过监测有关电路状态信号时域波形，再对其进行傅里叶变换获得频域传递函数值。

设x(nTs)是状态信号x(t)的采样，Ts为采样间隔，采样数据长度为 N。则离散傅里叶变换（Discrete Fourier Transform，DFT）算法如下：

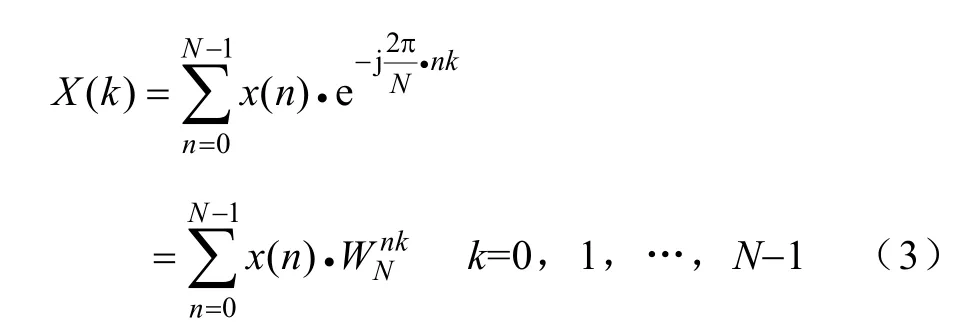
利用基2时析型快速傅里叶变换（Fast Fourier Transform，FFT）来实现 DFT。设 N=2M，M 为正整数，如果序列长度不满足2的整数次幂可在序列后补零。基2时析型FFT将输入时间序列x(n)按奇偶对分的原则分割序列得到奇、偶数号序列，即令n=2r和n=2r+1，r=0，1，…，N/2-1，于是

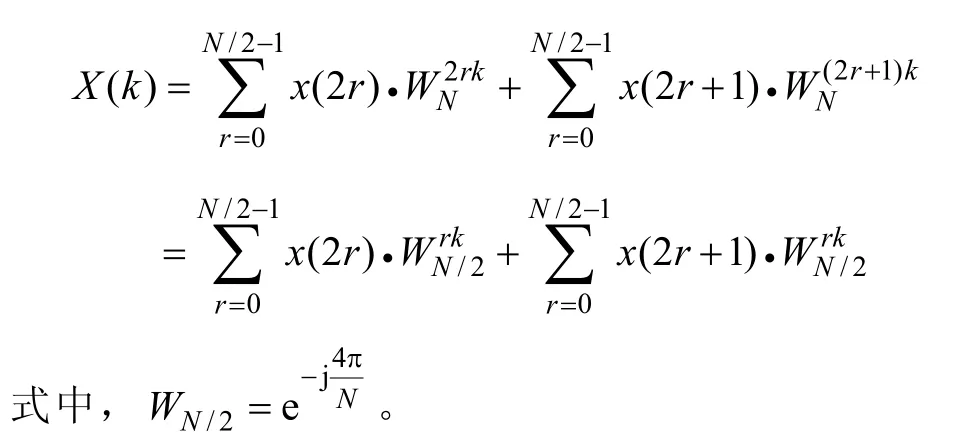
令

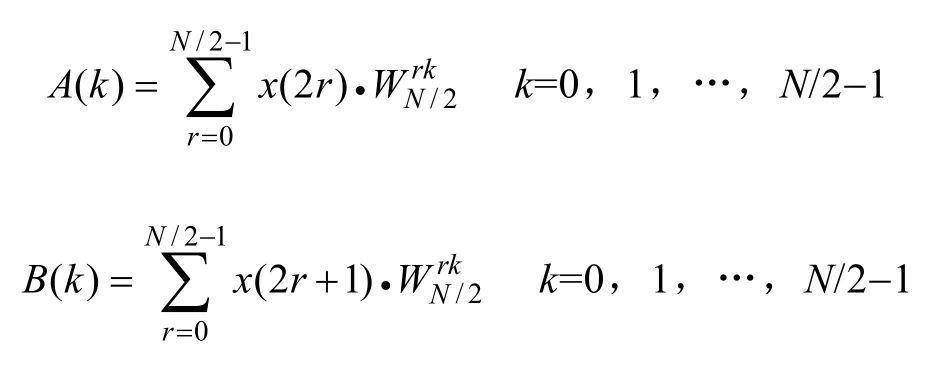
则输入序列x(n)的离散傅里叶变换为

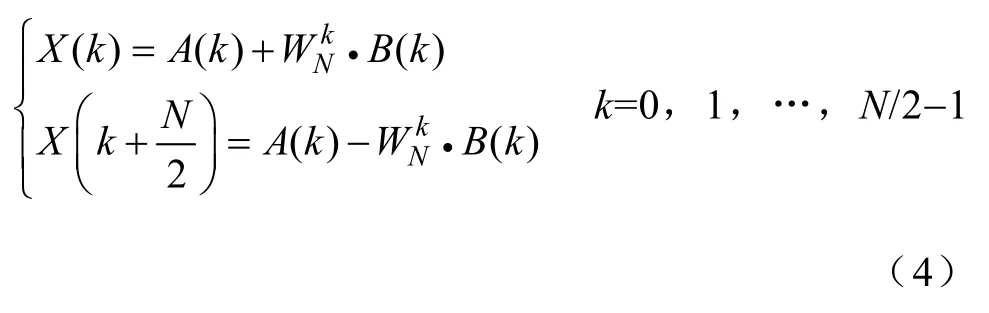
2.3 电路参数辨识

电力电子电路参数辨识的基本思路为：首先，根据电路原理建立电路频域模型；其次，获取电路状态监测信号，利用傅里叶分析得到电路频率响应特性；基于电路频域模型及频响特性，利用参数辨识算法进行模型参数估计。考虑到模型参数估计过程中，涉及多变量高次方程求解十分困难，为此，把电路参数估计问题转换成优化问题求解，利用遗传算法来实现电路参数辨识。

遗传算法（Genetic Algorithm，GA）是一类借鉴生物界的进化规律演化而来的随机搜索方法，具有简单通用、鲁棒性强，且不易陷入局部最优等优点，已被广泛地应用于组合优化、机器学习、信号处理、自适应控制及曲线拟合等领域。利用遗传算法对电力电子电路进行参数辨识，电路参数辨识算法实现流程如图3所示。算法实现主要过程如下：

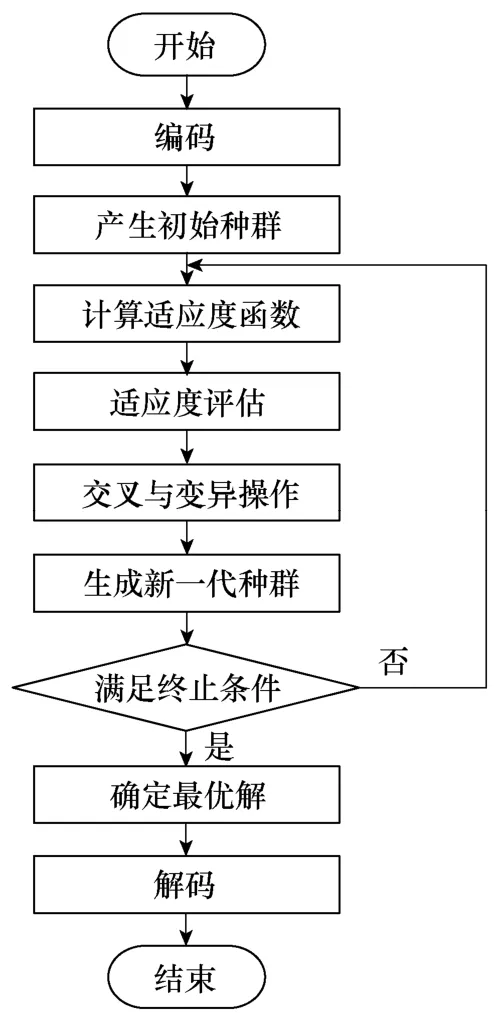
图3 电路参数辨识算法流程图Fig.3 Flow chart of circuit parameter identification method

（1）编码方案：根据电路中待求解元器件参数的变化范围，采用二进制编码及解码方案。

（2）适应度函数与适应度评估：把电路参数估计转换成目标优化问题。选择电路频域模型作为适应度函数，而实际电路频率响应特性作为理想适应度值（即对应的优化目标最佳值）。通过计算个体适应度值与最优适应度值之间的误差大小来判断个体的适应度优劣，利用遗传算法进化搜索得到最优的个体。最优个体解码就对应电路元器件参数，从而实现电力电子电路元器件参数辨识。

（3）遗传操作：交叉操作是把两个随机选择配对的染色体个体，按单点交叉方式相互交换其部分基因（交叉点按照概率选择），以形成两个新个体；变异操作是对染色体基因位进行概率变异，每个染色体基因位的变异概率相同。

（4）种群生成：初始种群是随机生成的，种群规模预先确定。在进化过程中，种群规模保持不变；采用最优个体保存策略，当前种群中适应度最高的个体不参与交叉和变异运算，而是直接复制到下一代；利用“轮盘赌比例选择法”来选择染色体，某个体被选择的概率取决于该个体的适应度值与全部个体适应度值之和的比值。随机选择两个个体进行遗传操作，以生成两个新个体。某个体的选择概率大，则能被多次选中，其遗传基因就会在种群中扩大，而某个体的选择概率小，则可能被淘汰。

（5）进化终止条件：当达到预定的进化代数，或者最优个体的适应度值与理想适应度值之差为某一阈值时，则进化过程终止。

（6）最优染色体解码，获得电路参数估计值。

3 实例分析

以图 1所示 Buck电路为例，采用数字仿真与实验方案来验证评估电路参数辨识方法的可行性与有效性。

3.1 电路频域模型响应特性结果分析

利用FFT方法获取Buck电路中电感输入端电压uin和电路输出电压uo的频域特性。电路正常时，uin、uo的频域响应特性分别如图4与图5所示。由图可知，频谱分量主要集中在开关频率f0=50kHz及f0的整数倍处，且在f0时最大。

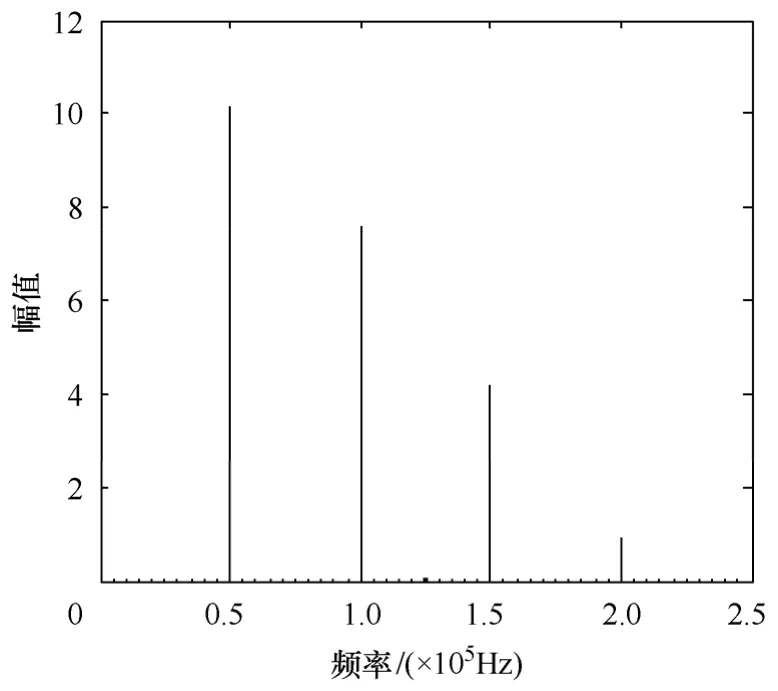
图4 电感输入端电压FFT频谱Fig.4 FFT spectrum of the inductor’s input voltage

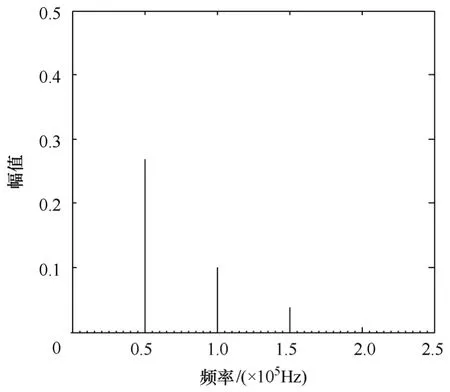
图5 输出电压FFT频谱Fig.5 FFT spectrum of the output voltage

3.2 电路参数辨识算法实现及结果分析

3.2.1 Buck电路参数辨识遗传算法编程实现

（1）编码。选用二进制编码方式对待估计参数进行编码。电路模型有四个未知参数，则设置每个染色体个体有4个基因段，每个参数对应的基因段有8个基因位，则染色体共有32位基因组成，各位所表示的含义见表1。

表1 染色体基因位含义表Tab.1 The present meaning of chromosome

设电容 C、串联电阻 RESR、电感 L和电阻 RL的变化范围分别为 220～130μF、0.45～1.35Ω、43～30μH、1.25～0.5Ω，将各参数的变化范围作为其编码与解码区间。

（2）选择算子。采用“轮盘赌”选择方法，每个个体进入下一代的概率为其适应度值与整个种群中个体适应度之和的比值。

（3）适应度函数及适应度评估。选择式（2）作为适应度函数，函数的模为适应度值。由式（2）可知，染色体适应度值是频率ω 和电路参数的函数。选择频率ω 作为电路频域传递函数的输入，实际测量计算得到的|H(jω)|作为理想适应度值。

适应度评估是在N点频率下计算染色体个体适应度值与理想适应度值之间的误差平方和来进行评估，误差平方和越小表明染色体越好。选择每代中误差平方和最小的个体作为本代的最优个体，并将本代的最优个体与进化过程中总体最优个体做比较，误差平方和最小的个体就是总体最优个体。

（4）交叉操作。在每一代个体中，若产生的随机数小于设定的交叉概率Pc=0.6，则随机选择两个染色体，且随机选择交叉点位置，在交叉点处交换基因实现父代的交叉。

（5）变异操作。变异过程是通过设置初始变异概率Pm=0.1，并随着进化代数的增加逐渐减小变异概率。

（6）终止条件。以终止代数、适应度误差作为进化过程结束条件。设定终止代数为5000代，适应度误差为0.135。

3.2.2 参数辨识结果及分析

对电路正常时及电解电容器、电感、负载电阻参数、所有器件参数发生变化五种典型情况分别进行电路仿真，监测电感输入电压和电路输出电压，通过FFT分析得到电路模型传递函数幅值，从中选择50～500kHz之间50kHz的整数倍频作为理想适应度计算和适应度评估的频率点，利用遗传算法进行电路参数辨识，有关结果见表2。

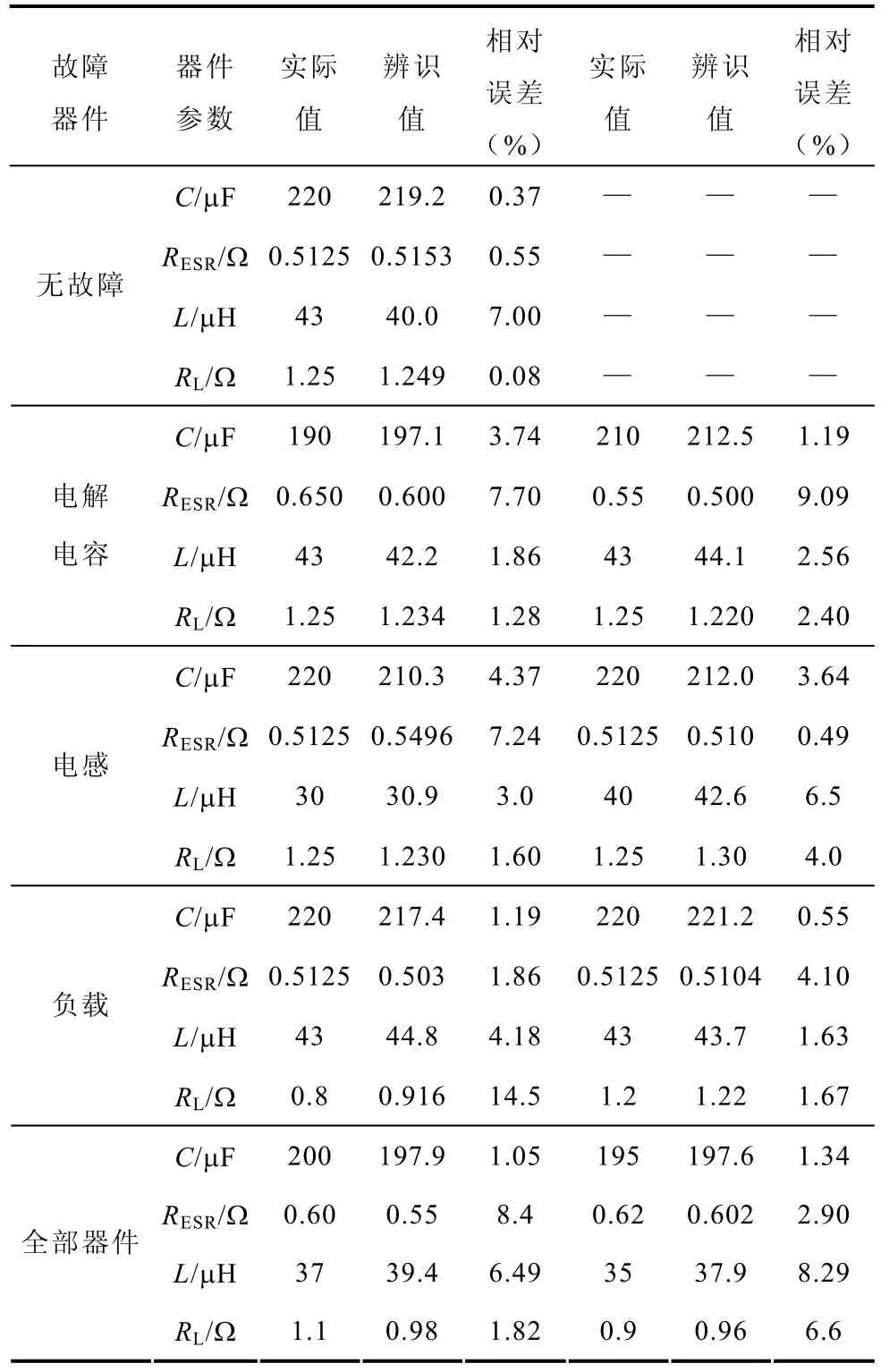
表2 仿真情况下Buck电路参数辨识结果Tab.2 The parameter identification results of Buck converter by simulation method

由表2可知，利用本文方法对电路元器件参数进行辨识，无故障时相对误差最小；当负载电阻为0.8Ω时，辨识误差最大，达到 14.5%。对电阻减小到1Ω以下的情况，做了多次实验，所得结果的误差都比较大。而对于电阻大于1Ω情况，则电阻辨识结果的相对误差都较小；经分析，辨识误差主要来源于FFT分析和遗传算法参数辨识过程中。不同元器件参数变化情况下的辨识结果相对误差都在15%之内，可认为本文方法能够实现Buck电路参数辨识。

3.3 电路参数辨识方法实验验证

为了验证所提出参数辨识方法对实际电路的参数辨识效果，搭建了 Buck实验电路。实验中开关频率为30kHz，电感L的标称值为100μH，电容C的标称值为2200μF，输出负载RL为2Ω。为便于测试数据分析，采用PCI—1714UL板卡来实时采集实验电路监测信号，A-D分辨率为12位，采样频率为600kHz。实验电路参数辨识结果见表 3，其中各元器件参数实际值是利用Agilent 4263B LCR分析仪测量得到。

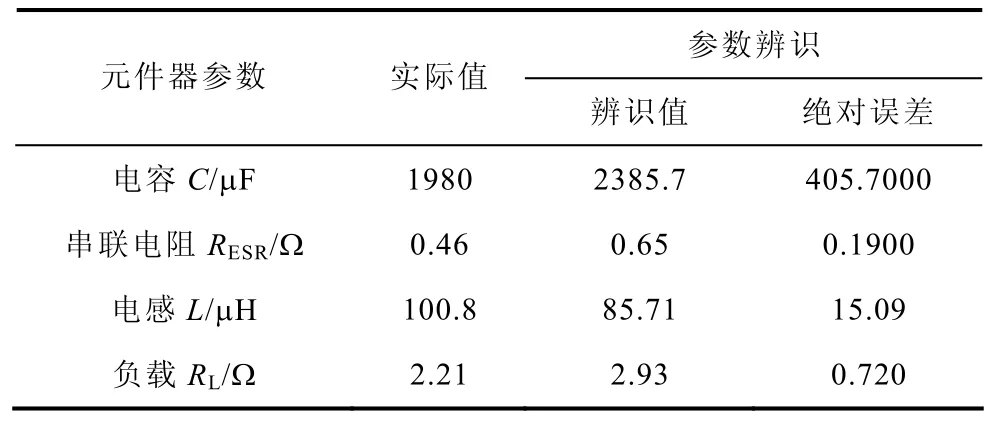
表3 Buck实验电路参数辨识结果Tab.3 The parameter identification results of experimental Buck converter

由表 3可知，本文方法能够进行电路参数辨识，但是与仿真数据辨识结果相比，实验电路参数辨识结果误差比较大。分析误差产生的主要原因有：

（1）噪声信号的影响。噪声是影响参数辨识结果的重要原因。实验 Buck电路是在面包板上连线搭建的，监测信号容易受到噪声影响，而电压信号中纹波包含许多有用的频谱分量，因纹波电压幅值较小受到噪声的影响也较大。

（2）监测信号采样精度的影响。因 A-D转换位数有限，而输出电压中直流分量大导致采样电压范围大，使得输出电压纹波信号部分的采样分辨率较小，则电路频域响应特性计算误差大，引起参数辨识结果误差大。

（3）FFT频谱分析和遗传算法参数辨识算法对电路元器件参数估计也有一定的计算误差影响。

4 结论

提出了一种基于电路频域建模和遗传算法参数求解的电力电子电路参数辨识方法。首先建立电路频域模型，再对电路监测信号进行FFT分析获得电路频域响应特性。然后，根据电路频域特性，通过把电路参数辨识转换成目标优化问题，利用遗传算法优化搜索实现电路参数辨识，避免了多变量高次方程的求解，通用性较好。以 Buck电路为例，通过仿真与实验验证了新方法是可行有效的。新的电路参数辨识方法能用于电力电子电路参数型故障诊断，但实际电路参数辨识结果精度还有待进一步提高，后续工作将深入研究采取措施以提高电路参数辨识精度，例如，监测信号噪声滤波、纹波电压精密采样等。

[1]Lall P, Hande M, Bhat C, et al. Prognostics health monitoring (PHM)for prior-damage assessment in electronics equipment under thermo-mechanical loads[C]. Proceedings of the Electronic Components and Technology Conference. New York, USA, 2007:1097-1111.

[2]Ma Zhangshan. A new life system approach to the prognostic and health management (PHM)with survival analysis, dynamic hybrid fault models,evolutionary game theory, and three-layer survivability analysis[C]. Proceedings of IEEE Aerospace Conference, Big Sky, Montana, USA, 2009: 1-20.

[3]Orsagh R, Brown D, Roemer M, et al. Prognostic health management for avionics system power supplies[C]. Proceedings of the IEEE Aerospace Conference, Big Sky, Montana, USA, 2005: 3585-3591.

[4]崔江, 王友仁, 刘权. 基于高阶谱与支持向量机的电力电子电路故障诊断技术[J]. 中国电机工程学报,2007, 27(10): 62-66.Cui Jiang, Wang Youren, Liu Quan. The technique of power electronic circuit fault diagnosis based on higher-order spectrum analysis and support vector machines[J]. Proceedings of the CSEE, 2007, 27(10):62-66.

[5]崔江, 王友仁. 采用基于模糊推理的分类器融合方法诊断电力电子电路参数故障[J]. 中国电机工程学报, 2009, 29(18): 54-59.Cui Jiang, Wang Youren. Testing the parametric faults of power electronic circuits applying classifiers fusion method based on fuzzy inference[J].Proceedings of the CSEE, 2009, 29(18): 54-59.

[6]肖岚, 李睿. 逆变器并联系统功率管开路故障诊断研究[J]. 中国电机工程学报, 2006, 26(4): 99-104.Xiao Lan, Li Rui. Research on open-circuit fault diagnosis of transistor in inverter paralleling system[J].Proceedings of the CSEE, 2006, 26(4): 99-104.

[7]汤清泉, 颜世超, 卢松升, 等. 三电平逆变器的功率管开路故障诊断[J]. 中国电机工程学报, 2008,28(21): 26-32.Tang Qingquan, Yan Shichao, Lu Songsheng, et al.Opencircuit fault diagnosis of transistor in three-level inverter[J]. Proceedings of the CSEE, 2008, 28(21):26-32.

[8]陈如清. 采用新型粒子群算法的电力电子装置在线故障诊断方法[J]. 中国电机工程学报, 2008, 28(24):70-74.Chen Ruqing. A novel PSO based on-line fault diagnosis approach for power electronic system[J].Proceedings of the CSEE, 2008, 28(24): 70-74.

[9]罗慧, 王友仁, 崔江, 等. 电力电子电路多源特征层融合智能故障诊断方法[J]. 电机与控制学报,2010, 14(4): 92-96.Luo Hui, Wang Youren, Cui Jiang, et al. Intelligent fault diagnosis for power electronic circuits based on multi-source feature-level fusion[J]. Electric Machines and Control, 2010, 14(4): 92-96.

[10]Shetty P, Mylaraswamy D, Ekambaram T, et al. A hybrid prognostic model formulation system identification and health estimation of auxiliary power units[C]. Proceedings of the IEEE Aerospace Conference, Big Sky, Montana, USA, 2006: 10.

[11]马皓, 毛兴云, 徐德鸿. 基于混杂系统模型的DC/DC电力电子电路参数辨识[J]. 中国电机工程学报, 2005, 25(10): 50-54.Ma Hao, Mao Xingyun, Xu Dehong. Parameter identification of DC-DC power electronic circuit based on hybrid system model[J]. Proceedings of the CSEE, 2005, 25(10): 50-54.

[12]张志学, 马皓, 毛兴云. 基于混杂模型系统理论的电力电子电路故障诊断[J]. 中国电机工程学报,2005, 25(3): 49-53.Zhang Zhixue, Ma Hao, Mao Xingyun. Fault diagnosis for power electronic circuit based on hybrid system theory and event identification[J]. Proceedings of the CSEE, 2005, 25(3): 49-53.