非正弦激励下磁心损耗的计算方法及实验验证
张 宁 李 琳 魏晓光
(1.新能源电力系统国家重点实验室(华北电力大学) 北京 102206 2.全球能源互联网研究院 北京 102209)
非正弦激励下磁心损耗的计算方法及实验验证
张宁1李琳1魏晓光2
(1.新能源电力系统国家重点实验室(华北电力大学)北京102206 2.全球能源互联网研究院北京102209)
在电力电子装置中,磁性元件的输入电压波形往往不是正弦波,研究非正弦激励下电力电子装置中磁心损耗的计算方法有重要意义。首先介绍正弦激励下磁心损耗的计算方法,在此基础上研究了非正弦激励下磁心损耗的计算方法,得到了修正铁耗分离法和修正Steinmetz经验公式法计算式。其次,考虑磁心叠片的趋肤效应,对修正铁耗分离法做了进一步改进。然后,对环形非晶和纳米晶磁心的损耗测量结果进行数值拟合,得到了非正弦激励下两种方法的解析计算式,并比较了应用两种计算方法的损耗计算结果。最后,分别对环形非晶和纳米晶磁心开展非正弦激励下的磁心损耗测量实验,将实验结果和上面两种计算方法的解析结果进行比较,验证了非正弦激励下两种计算方法的准确性。
非正弦激励磁心损耗修正铁耗分离法修正Steinmetz经验公式法
0 引言
随着高压直流输电及电力电子技术的快速发展,磁性元件在整流器、逆变器和高频变压器等电力电子装置中的应用越来越广泛[1-7]。在电力电子装置中,磁性元件的激励波形往往不是正弦波,而是方波、矩形波和三角波等,且工作频率可能会达到兆赫兹。随着工作频率的提高,磁心损耗和温升也会相应提高[8-10],因此,准确计算非正弦激励下的磁心损耗就显得十分重要。
正弦激励下的磁心损耗的工程计算方法主要有铁耗分离法和Steinmetz经验公式法。铁耗分离法是按照磁心损耗产生的物理机理,将损耗分解成磁滞损耗、涡流损耗和剩余损耗。文献[11]给出了在正弦激励下磁滞损耗、涡流损耗和剩余损耗的计算公式。而Steinmetz经验公式法是将三部分损耗用一个经验公式来计算的方法,在正弦波激励下,能较准确地计算磁心损耗[12]。
为了计算非正弦激励下的磁心损耗,文献[13]对磁滞损耗和涡流损耗产生的不同物理机理进行了详细分析,提出了一种脉冲电压激励条件下磁心涡流损耗的计算方法,并对铁氧体磁心在不同占空比时矩形波激励下进行了磁心损耗测量。文献[14]给出了在任意波形激励下涡流损耗和剩余损耗的通用计算式,对典型非正弦激励波形下的涡流损耗和剩余损耗进行了计算。对铁氧体磁心在方波和PWM波激励下进行了磁心损耗测量,将实验测量结果和计算结果进行了比较。但是,文中没有具体给出非正弦激励下磁心总损耗的计算式。文献[15]对涡流损耗产生的机理进行详细的分析,给出了在任意波形激励下涡流损耗的通用计算式,并对铁氧体磁心在正弦激励下进行了损耗测量,将实验结果和计算结果进行了比较。但文中也没有给出非正弦激励下磁心总损耗的计算式。文献[16]介绍了非正弦激励下计算磁心损耗的修正Steinmetz经验公式法,但没有在非正弦激励下对磁心损耗开展实验验证。文献[17]介绍了非正弦激励下计算磁心损耗的修正Steinmetz经验公式法,对铁氧体磁心在三角波激励下进行了损耗测量,并将测量结果和修正Steinmetz经验公式法计算结果进行了比较。上述文献中都没有考虑趋肤效应对非正弦激励下磁心损耗计算方法的影响。
本文基于正弦激励下磁心损耗计算方法推导了非正弦激励下磁心损耗的工程计算方法,得到修正铁耗分离法和修正Steinmetz经验公式法计算公式,又对修正铁耗分离法做了进一步的改进。通过测量环形非晶和纳米晶磁心在正弦激励下不同频率和磁通密度时的损耗,数值拟合得到了上述两种方法的解析计算式,最后,将实验测量结果和上面两种方法的解析结果进行了比较,验证非正弦激励下两种计算方法的准确性。
1 正弦激励下磁心损耗计算方法
正弦激励下磁心损耗的计算方法主要有两种,即铁耗分离法和Steinmetz经验公式法。
铁耗分离法是Bertotti提出的,根据磁心损耗产生的不同机理,将磁心损耗分解成磁滞损耗、涡流损耗和剩余损耗。Bertotti铁耗分离法忽略了磁心的趋肤效应,得到的正弦激励下铁耗分离法计算式为[11,18]
(1)
式中,Ch、Cce和Cex分别为磁滞损耗系数、涡流损耗系数和剩余损耗系数;α为磁通密度指数。
一般只要对正弦激励下实验测量得到的磁心损耗数据进行拟合,就可以得到磁心损耗系数和磁通密度指数值,进而得到铁耗分离法的解析计算式。
Steinmetz经验公式法可表示为[12]
(2)
式中,Pcv为磁心损耗密度;km、α和β为损耗系数。
Steinmetz经验公式法忽略了磁心形状以及尺寸的影响,认为磁心损耗密度仅取决于磁心材料、工作频率以及磁通密度峰值。磁心损耗系数一般通过厂家或实验室测量得到,Steinmetz经验公式法简化了磁心损耗的计算,适合工程应用。
但是,铁耗分离法和Steinmetz经验公式法都仅适应于正弦激励下磁心损耗计算。在计算非正弦磁心损耗时,需要对它们进行修正。
2 非正弦激励下磁心损耗计算方法
2.1修正铁耗分离法
磁滞损耗是磁性材料在磁化过程中克服磁畴壁的摩擦所消耗的能量。对于同一磁心,在任意激励波形下,只要磁通密度变化幅值及频率相同,其磁滞损耗就相同,即激励波形对磁滞回线的影响可以忽略[14-19],磁滞损耗大小与频率呈正比,即
(3)
因此,对于同一磁心,在相同磁通密度变化幅值和频率下,不同激励波形时的磁心损耗差异主要来自于涡流损耗和剩余损耗。涡流损耗大小与磁通密度的变化率和磁心的电阻率等有关,磁心的涡流损耗计算模型[15]如图1所示。

图1 磁心涡流损耗计算模型Fig.1 Calculation model of eddy current loss of core
为了计算磁心中总涡流损耗,将图1a中圆柱型磁心分解成多个圆环形磁心单元,如图1b所示,磁心单元厚度为dr。根据电磁感应定律,可以得到在磁心单元中交变磁通产生的感应电动势。所以,计算得到磁心单元涡流损耗为
(4)
式中,磁心单元感应电动势和磁心单元电阻分别为
(5)
(6)
对于图1a中磁心总涡流损耗的计算,需要在0~r0范围内对式(4)进行积分,得到
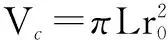
对式(7)在一个周期内积分,得到其平均涡流损耗为
(8)
根据式(8),计算得到正弦激励下涡流损耗为
(9)式中,ρ为电阻率;Bm为磁通密度峰值;f为正弦激励频率。
方波激励波形如图2所示,最大占空比为
(10)
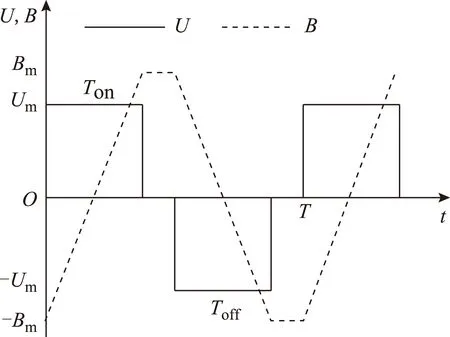
图2 存在死区时间方波激励及磁通波形Fig.2 Square wave with dead time and flux density curve
根据式(8),得到图2方波激励涡流损耗为
(11)
对于同一磁心,在相同磁通密度变化幅值和频率下,根据式(11)与式(9),计算得到方波激励下涡流损耗和正弦波激励下涡流损耗的比值为
(12)
矩形波激励波形和对应磁通波形如图3所示。
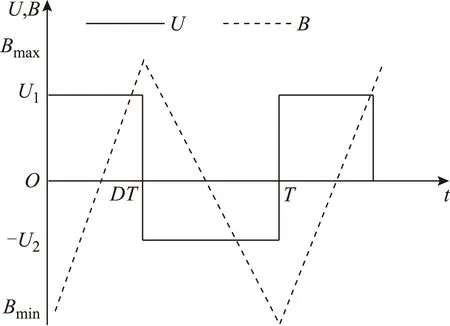
图3 矩形波激励及磁通波形Fig.3 Rectangular wave and flux density curve
根据式(8),计算得到矩形波激励下涡流损耗和正弦激励下涡流损耗比值如下。其中,波形占空比D如图3所示,且U1·DT=U2·(1-D)T。
(13)
三角波激励波形和对应磁通波形如图4所示。同样,根据式(8),计算得到三角波激励下涡流损耗和正弦激励下涡流损耗比值如下,其中,波形占空比D如图4所示。
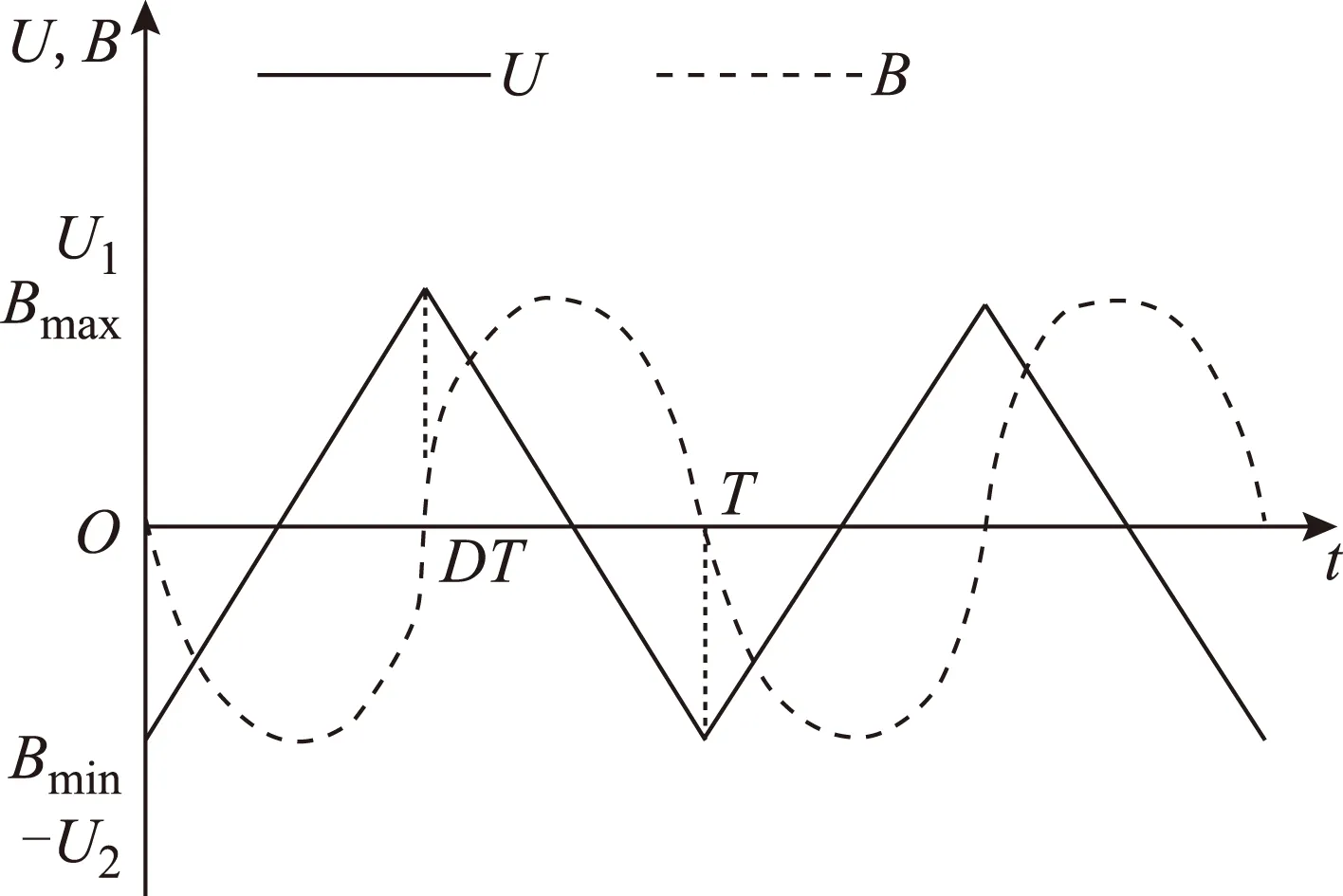
图4 三角波激励及磁通波形Fig.4 Triangle wave and flux density curve
(14)
上面涡流损耗的推导没有考虑磁心趋肤效应。当磁心叠片的厚度大于趋肤深度时,需要考虑趋肤效应。计算模型如图5所示。
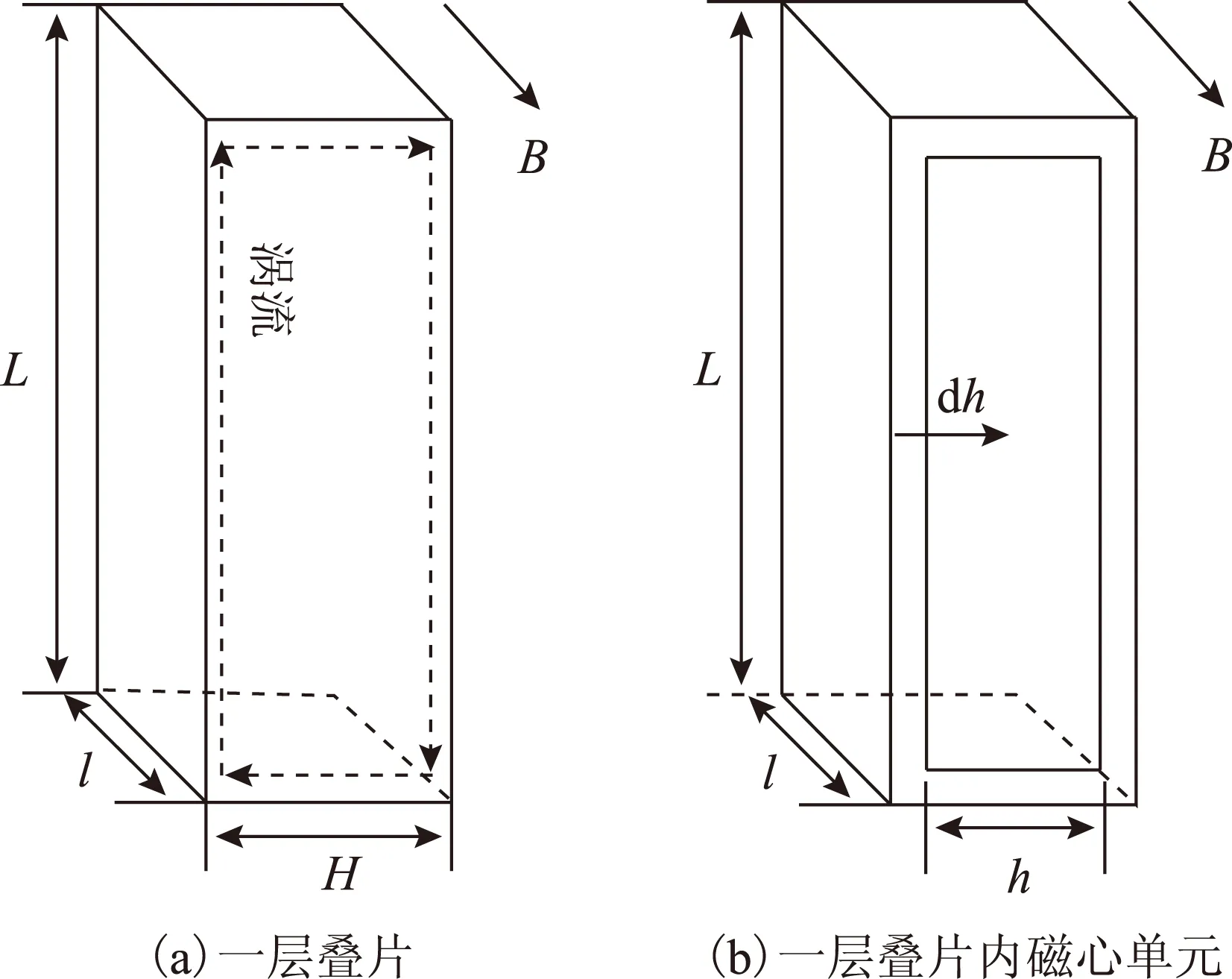
图5 磁心一层叠片Fig.5 A piece of laminate of core
为了计算一层叠片的涡流损耗,将其分成图5b所示磁心单元。其中,H为一层叠片厚度,L为叠片的宽度,l为叠片的长度,dh为一层叠片内磁心单元厚度,h为叠片内磁心单元的窗口厚度。由于叠片宽度L远大于叠片厚度H,且叠片宽度L也远大于趋肤深度。
在一层磁心单元内,由于磁心单元厚度h值很小,所以,认为磁心单元内的磁通密度是均匀的,磁心单元的宽度仍取L,所以,磁心单元的电阻和交变磁通在磁心单元中产生的感应电动势分别为
(15)
(16)
根据式(15)和式(16),计算得到图5b所示磁心单元的涡流损耗为
(17)
通常铁心叠片厚度很小,在工程计算时,可以近似认为趋肤深度δ内的电流密度分布是均匀的。进而,对式(17)在0~δ内进行积分,并结合式(15)和式(16),计算得到考虑趋肤效应时涡流损耗为
(18)
式中,δ为趋肤深度。
(19)
式中,μ为磁心磁导率;ρ为磁心电阻率。
由于h远小于L,所以,式(18)简化为
(20)
根据式(20),计算得到考虑趋肤效应时瞬时涡流损耗为
(21)
对式(21)在一个周期内的积分,得到其平均涡流损耗为
(22)
根据式(22),并结合式(19),计算得到正弦激励下考虑趋肤效应时涡流损耗为
(23)
对于如图2所示的方波激励波形,利用同样的方法,根据式(22),计算得到方波激励下考虑趋肤效应时涡流损耗为
(24)
对于同一磁心,在相同磁通密度变化幅值和频率下,将式(24)与式(23)建立比值,所以,利用同样的方式,计算得到方波、矩形波和三角波激励下涡流损耗和正弦波激励下涡流损耗的比值分别为
(25)
(26)
(27)
剩余损耗是磁心中弛豫效应引起的损耗,与磁性材料特性和工作频率等密切相关,根据Bertotti理论[11],剩余损耗计算式为
(28)
式中,α为常数;n0为两个磁性物体之间的磁场强度差相关的常数;Vc为磁心体积;Ac为磁心的截面积;ρ为磁心电阻率。
根据式(28),计算得到正弦激励下剩余损耗为
(29)
对于图2~图4所示的非正弦激励波形,计算得到在相同磁通密度变化幅值和频率下,非正弦激励波形下剩余损耗和正弦激励下剩余损耗比值分别为
(30)
(31)
(32)
式中,D为占空比,如图2~图4所示。
所以,基于上述对磁滞损耗、涡流损耗和剩余损耗的计算与分析,归纳起来,在不考虑磁心叠片的趋肤效应时,修正铁耗分离法计算式为
(33)
在考虑叠片趋肤效应时,对修正铁耗分离法计算式做进一步的改进,得到的计算式为
(34)
式中,Ch、Cce、Cex和α系数以及Ch-skin、Cce-skin、Cex-skin和β系数都是基于正弦波激励下的磁心损耗数据拟合得到的。
所以,已知正弦波激励下铁耗分离法计算式,和非正弦激励下涡流损耗、剩余损耗与正弦激励下涡流损耗、剩余损耗的比值,就能得到非正弦激励下的修正铁耗分离法计算式。
2.2修正Steinmetz经验公式法
正弦激励下Steinmetz经验公式法是计算正弦激励下磁心损耗常用的方法,但是,对于非正弦激励下,不能直接应用该法。为此,文献[17]提出了修正Steinmetz经验公式法来计算磁心损耗。Takada通过对几种不同激励电压作用下的磁心损耗进行测试,得出结论:磁心损耗和宏观的重复磁化速率有直接关系,而磁化速率与磁通密度的平均变化率呈正比[20]。
因此,在非正弦激励下单位磁心体积损耗的修正Steinmetz经验公式法计算式为
(35)
式中,km、α和β为同一磁心材料在正弦激励下的Steinmetz经验公式中参数;f为非正弦激励波形频率;feq为非正弦激励下等效正弦磁化频率。
(36)
ΔB=Bmax-Bmin=2Bm
(37)
对于图2~图4所示非正弦激励波形,只需要计算等效正弦磁化频率feq,带入式(35)中,即可得到对应磁心损耗计算式,所以,计算得到方波、矩形波和三角波激励下等效正弦磁化频率分别为
(38)
(39)
(40)
2.3基于实验测量的解析计算式
环形非晶和纳米晶磁心的尺寸均为外径50mm,内径32mm,高度为20mm,磁心均为带绕磁心。对于非晶磁心,每层薄带厚度为0.03mm;对于纳米晶磁心,每层薄带厚度为0.025mm。利用实验室软磁交流测试系统,分别测量了环形非晶和纳米晶磁心在正弦波激励下不同磁通密度和频率时磁心损耗值,数据见表1和表2。
分别对环形非晶和纳米晶磁心在正弦波激励下的损耗测量数据进行数值拟合处理,结合上面非正弦激励下两种计算方法的磁心损耗计算式,得到环形非晶和纳米晶磁心在方波激励下修正铁耗分离法和修正Steinmetz经验公式法的解析计算式。
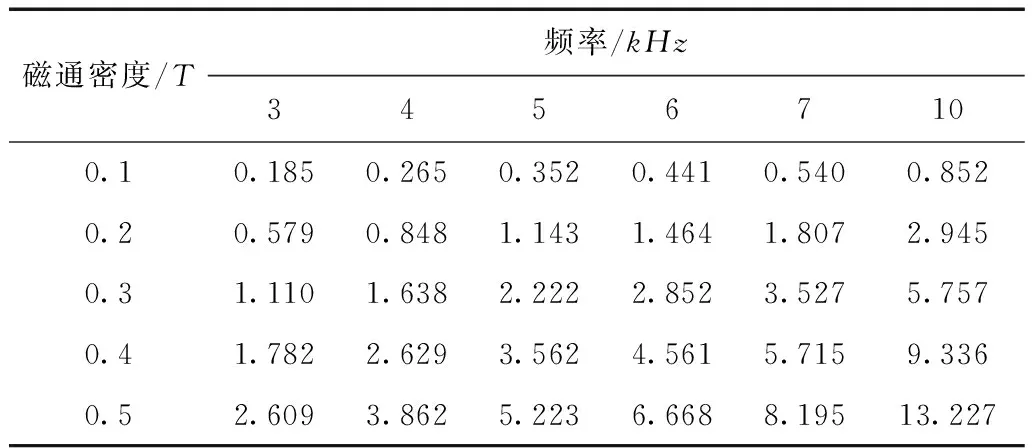
表1 正弦激励下非晶磁心损耗Tab.1 Amorphous core loss under sine wave (单位:W)
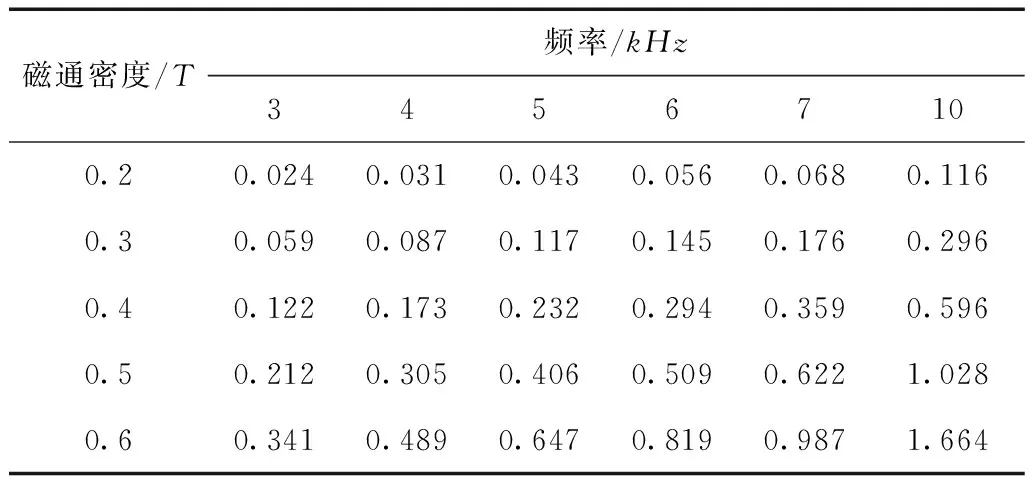
表2 正弦激励下纳米晶磁心损耗Tab.2 Nanocrystalline core loss under sine wave (单位:W)
环形非晶磁心修正铁耗分离法解析计算式为
(41)
环形非晶磁心修正Steinmetz经验公式法解析计算式为
(42)
环形纳米晶磁心修正铁耗分离法解析计算式为
(43)
环形纳米晶磁心修正Steinmetz经验公式法解析计算式为
(44)
式中,Vc为23.04cm3。
从式(41)和式(43)可以看出,剩余损耗相比磁滞损耗和涡流损耗很小,因此,对于非晶和纳米晶磁心,在利用修正铁耗分离法计算非正弦激励下磁心损耗时,可以忽略剩余损耗。
对于其他非正弦激励波形下磁心损耗的计算,只需要将式(41)~式(44)中方波激励涡流损耗和剩余损耗与正弦波激励对应损耗比值或者等效正弦磁化频率替换为对应波形激励与正弦波激励下涡流损耗和剩余损耗比值或等效正弦磁化频率即可。
根据解析计算式(41)~式(44),分别计算环形非晶和纳米晶磁心在3kHz,不同磁通密度时方波激励下的磁心损耗,计算结果见表3和表4。
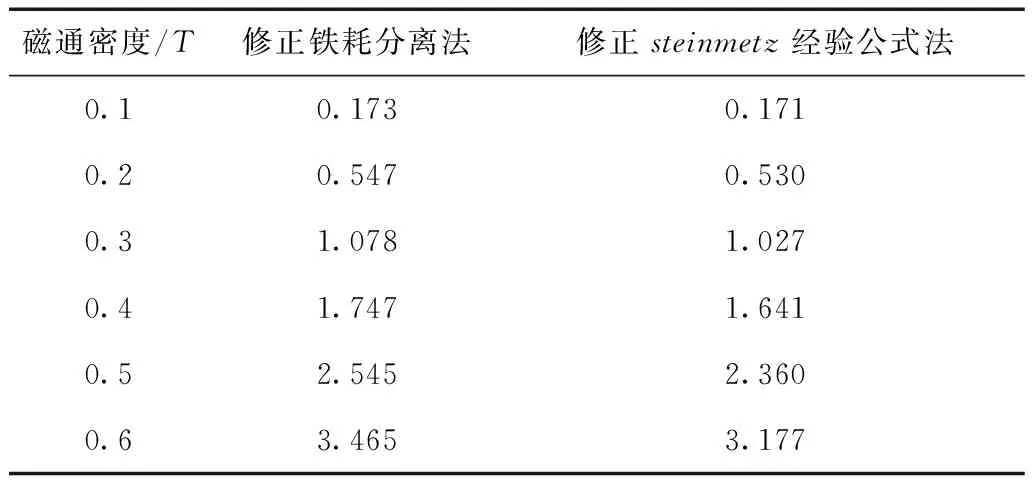
表3 3 kHz,D=1,不同磁通密度时非晶磁心 在方波激励下磁心损耗Tab.3 Loss of amorphous core under square wavewith 3 kHz,D=1 and different flux density (单位:W)
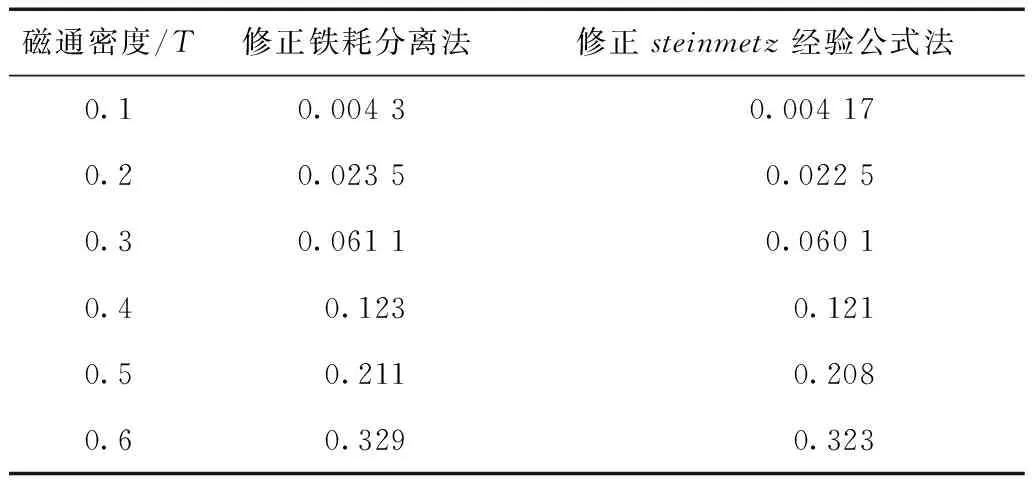
表4 3 kHz,D=1,不同磁通密度时纳米晶磁心 在方波激励下磁心损耗Tab.4 Loss of nanocrystalline core under square wavewith 3 kHz,D=1 and different flux density (单位:W)
从表3和表4中可以看出,对于环形非晶和纳米晶磁心,在方波激励下,修正铁耗分离法和修正Steinmetz经验公式法的磁心损耗计算结果相差很小,经过比较,相互验证了两种计算方法的有效性。
对于非晶和纳米晶磁心,由于每层薄带厚度很小,分别为0.03mm和0.025mm,而实验室测量仪器输出的最高频率为5kHz。因此,根据趋肤深度计算式(19)知,在实验条件下,非晶和纳米晶磁心的趋肤效应很小,对磁心损耗的影响很小。所以,利用修正铁耗分离法的损耗计算结果就没有考虑磁心趋肤效应影响。
在两种计算方法中,修正Steinmetz经验公式法计算参数少。且修正Steinmetz经验公式法中对应参数一般厂家会提供或者在实验室测量并通过拟合计算得到,同时,对于同一材料不同结构和尺寸大小的磁心,其参数仍然适应。而对于修正铁耗分离法来说,如果磁心尺寸发生改变,其计算参数值就会相应发生改变,需要重新进行数值拟合计算。所以,经过比较,修正Steinmetz经验公式法应用更方便。
3 损耗测量及验证
利用可编程电源分别对相同尺寸环形非晶和纳米晶磁心进行空载试验,测量它们的磁心损耗。试验中环形非晶和纳米晶磁环尺寸均为外径50mm,内径32mm、高20mm。可编程电源输出的频率范围为0.04~5kHz,可以输出方波等非正弦波形,同时,可以直接从可编程电源对应的操作软件界面上读取实际输出电压、电流有效值及功率因数。
由于可编程电源输出最大频率为5kHz,所以,在实验条件下,非晶和纳米晶磁心的趋肤效应很小。在此,对于修正铁耗分离法的计算结果,就不考虑其趋肤效应,空载试验的测量电路如图6所示。
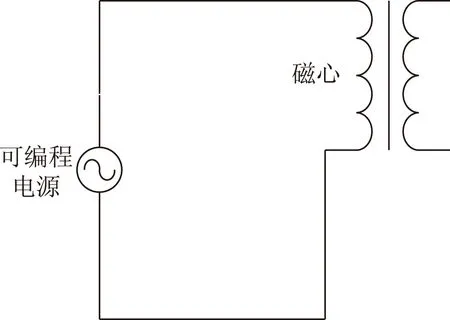
图6 空载试验电路Fig.6 No-load experimental circuit
在磁心的空载试验中,测量得到方波激励下,不同磁通密度时可编程电源输出电压、电流有效值和功率因数。但由于磁心尺寸小,绕线匝数少,且导线电阻和测量的空载电流也很小,所以,利用测量数据计算磁心损耗时,就不考虑绕组损耗。
对于纳米晶磁心,在Bm=0.6T,输出3kHz、D=1时,可编程电源输出的方波电压波形如图7所示。
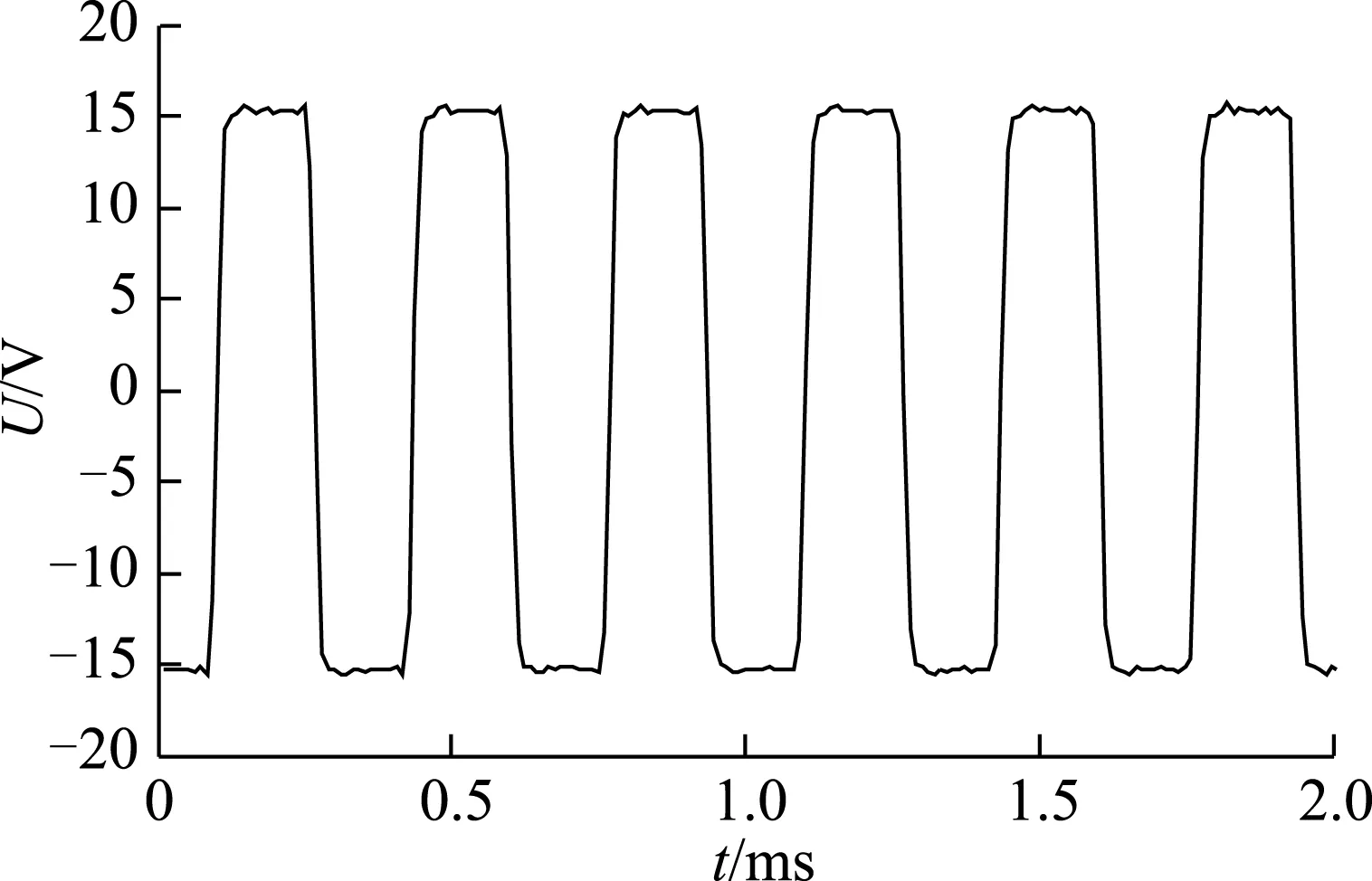
图7 Bm=0.6 T时输出的3 kHz、D=1方波电压波形Fig.7 Square wave voltage of 3 kHz,D=1,Bm=0.6 T
将环形非晶和纳米晶磁心在方波激励下的损耗测量结果和根据2.3节式(41)~式(44)的磁心损耗解析计算结果共同绘成如图8和图9所示的图形。
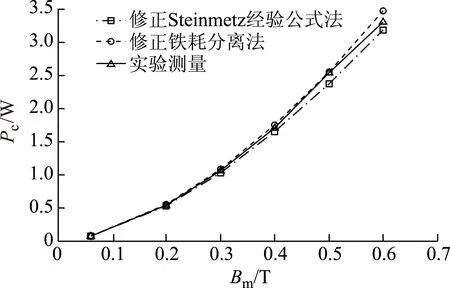
图8 3 kHz,D=1时方波激励下非晶磁心损耗结果对比Fig.8 Contrast of core loss of amorphous core with 3 kHz,D=1 under square wave
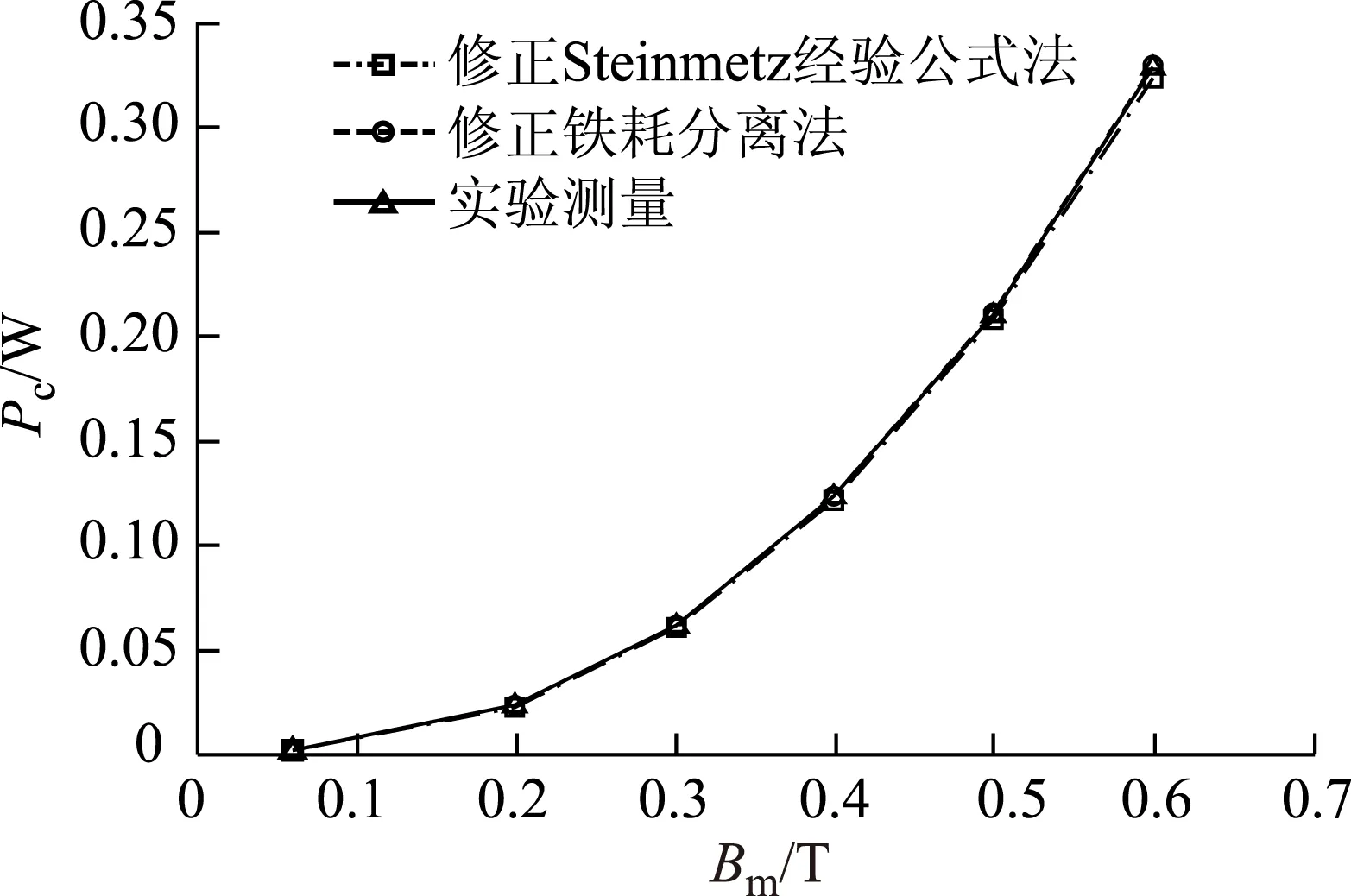
图9 3 kHz,D=1时方波激励下纳米晶磁心 损耗结果对比Fig.9 Contrast of core loss of nanocrystalline core with 3 kHz,D=1 under square wave
从图8和图9中可以看出,对于环形非晶和纳米晶磁心,在方波激励下,两种方法的解析计算结果与实验测量结果相差很小,由此验证了两种方法计算的准确性。同时,从图8和图9看出,磁心损耗实验测量值和没有考虑磁心趋肤效应时的修正铁耗分离法计算值更吻合,说明了非晶和纳米晶磁心在实验条件下没有发生趋肤效应。但是,如果磁心发生趋肤效应,那么磁心的涡流损耗就会减小,磁心损耗实际测量值也就会减小,此时,就需要采用考虑趋肤效应时的修正铁耗分离法来进行数值拟合才更准确。对比图8和图9还能看出,在相同磁通密度和频率时,纳米晶磁心损耗远小于非晶磁心损耗,所以,在高频下选择磁心材料时,优先考虑纳米晶。
4 结论
通过与实验测量结果进行比较,验证了本文给出的修正铁耗分离法解析计算式和修正Steinmetz经验公式法解析计算式的准确性,本文还考虑了磁心趋肤效应的影响,对修正铁耗分离法解析计算式做了进一步的改进,扩大了修正铁耗分离法在高频下趋肤效应时的适应性。在非正弦激励下磁心损耗的两种计算方法中,修正Steinmetz经验公式法所需参数少,且适应性强,应用起来更加方便,很适合于工程应用中非正弦激励下磁性元件的磁心损耗计算。
[1]兰征,涂春鸣,肖凡,等.电力电子变压器对交直流混合微网功率控制的研究[J].电工技术学报,2015,30(23):50-57.
LanZheng,TuChunming,XiaoFan,etal.ThepowercontrolofpowerelectronictransformerinhybridAC-DCmicrogrid[J].TransactionsofChinaElectrotechnicalSociety,2015,30(23):50-57.
[2]周洁敏,赵秀科,陶思钰.开关电源中磁性元件理论及设计[M].北京:北京航空航天大学出版社,2014.
[3]曹晓冬,谭国俊,王从刚,等.三电平PWM整流器多模型预测控制方法[J].电工技术学报,2014,29(8):142-150.
CaoXiaodong,TanGuojun,WangConggang,etal.Researchonmulti-modelpredictivecontrolstrategyofthree-levelPWMrectifier[J].TransactionsofChinaElectrotechnicalSociety,2014,29(8):142-150.
[4]陈新,韦徵,胡雪峰,等.三相并网逆变器LCL滤波器的研究及新型有源阻尼控制[J].电工技术学报,2014,29(6):71-79.ChenXin,WeiZhi,HuXuefeng,etal.ResearchonLCLfilterinthree-phasegrid-connectedinverterandnovelactivedampingcontrolstrategy[J].TransactionsofChinaElectrotechnicalSociety,2014,29(6):71-79.
[5]马俊民,黄永瑞,何青连.±800kV特高压直流输电系统谐波研究[J].电力系统保护与控制,2013,41(21):33-37.
MaJunmin,HuangYongrui,HeQinglian.Researchonharmonicsof±800kVultrahighvoltagedirectcurrenttransmissionsystem[J].PowerSystemProtectionandControl,2013,41(21):33-37.
[6]蒋冠前,李志勇,杨慧霞,等.柔性直流输电系统拓扑结构研究综述[J].电力系统保护与控制,2015,43(15):145-153.
JiangGuanqian,LiZhiyong,YangHuixia,etal.ResearchreviewontopologicalstructureofflexibleHVDCsystem[J].PowerSystemProtectionandControl,2015,43(15):145-153.
[7]胡鹏飞,江道灼,郭捷,等.基于混合型多电平换流器的柔性直流输电系统[J].电力系统保护与控制,2013,41(10):33-38.
HuPengfei,JiangDaozhuo,GuoJie,etal.VSC-HVDCsystembasedonhybridmultilevelvoltagesourcedconverters[J].PowerSystemProtectionandControl,2013,41(10):33-38.
[8]孔剑虹,何湘宁,钱照明,等.功率变换器电感在直流偏置或矩形波激励时磁损问题研究[J].电工技术学报,2005,20(5):13-19,29.
KongJianhong,HeXiangning,QianZhaoming,etal.Corelossesofmagneticcomponentsinpowerconvertertopologies[J].TransactionsofChinaElectrotechnicalSociety,2005,20(5):13-19,29.
[9]颜冲,何俊,郭小东.不同激励条件下对铁氧体磁心损耗影响[J].磁性材料及器件,2011,42(2):37-42.YanChong,HeJun,GuoXiaodong.Influenceofdifferentexcitationwaveformsonferritecoreloss[J].JournalofMagneticMaterialsandDevices,2011,42(2):37-42.
[10]陈为,余素胜,罗恒廉,等.不同占空比脉冲电压激励下的高频磁损耗[J].电工电能新技术,1998,17(4):14-17.ChenWei,YuSusheng,LuoHenglian,etal.HFcorelossesunderpulseexcitationwithdifferentdutycycle[J].AdvancedTechnologyofElectricalEngineeringandEnergy,1998,17(4):14-17.
[11]BogliettiA,CavagninoA,LazzariM,etal.Predictingironlossesinsoftmagneticmaterialswitharbitraryvoltagesupply:anengineeringapproach[J].IEEETransactionsonMagnetics,2003,39(2):981-989.
[12]ProteusSC.Onthelawofhysteresis[J].TransactionsoftheAmericanInstituteofElectricalEngineers,1984,72(2):197-221.
[13]周岩.高频矩形波激励下磁心损耗的研究[J].电力自动化设备,2013,33(1):91-95.
ZhouYan.Magneticcorelossexcitedbyhigh-frequencyrectanglewaveform[J].ElectricPowerAutomationEquipment,2013,33(1):91-95.
[14]WaseemA.Apractical,accurateandverygeneralcorelossmodelfornonsinusoidalwaveforms[J].IEEETransactionsonPowerElectronics,2007,22(1):30-40.
[15]RoshenWA.Ferritecorelossforpowermagneticcomponentsdesign[J].IEEETransactionsonMagnetics,1991,27(6):4407-4415.
[16]旷建军,郑力新,卢小芬,等.非正弦励磁下磁心损耗的计算[J].磁性材料及器件,2009,40(1):44-46.KuangJianjun,ZhengLixin,LuXiaofen,etal.Calculationofcorelossesundernonsinusodialexcitation[J].JournalofMagneticMaterialsandDevices,2009,40(1):44-46.
[17]ReinertJ,BrockmeyerA,DeD,etal.Calc-ulationoflossesinferroandferromagneticmaterialsbasedonthemodifiedsteinmetzeauation[J].IEEETransactionsonIndustryApplications,2001,37(4):1055-1061.
[18]周岩,杨长业,谢俊.高频铁氧体功率损耗分离方法及其应用[J].磁性材料及器件,2013,44(6):50-54.
ZhouYan,YangChangye,XieJun.Separationofhighfrequencyferritecorepowerlossanditsapplication[J].JournalofMagneticMaterialsandDevices,2013,44(6):50-54.
[19]SakakiY,MatsuokaT.HysteresislossesinMn-Znferritecores[J].IEEETransactionsonMagnetics,1986,22(5):623-625.
[20]TakadaS,SasakiT.Powerlossesofsoftmagneticferriteundercontrolledmagnetizingcondition[J].IEEETransactionsonMagnetics,1995,31(6):4056-4058.
Calculation Method and Experimental Verification of Core Losses Under Non-Sinusoidal Excitation
Zhang Ning1Li Lin1Wei Xiaoguang2
(1.StateKeyLaboratoryofAlternateElectricalPowerSystemwithRenewableEnergySourcesNorthChinaElectricPowerUniversityBeijing102206China2.GlobalEnergyInterconnectionResearchInstituteBeijing102209China)
Inpowerelectronicsdevices,theinputvoltageofmagneticcomponentsisoftennon-sinusoidalwave.Soitissignificanttostudythecalculationmethodofcorelossesundernon-sinusoidalexcitation.Firstly,thecalculationmethodofcorelossesundersinusoidalexcitationisintroduced.Thenthecalculationmethodsofcorelossesundernon-sinusoidalexcitationareresearched.ThecalculationformulaofthemodifiedironlossesseparationmethodandthemodifiedSteinmetzempiricalformulamethodareacquiredaccordingly.Secondly,byconsideringtheskineffectofthecore,furthermodificationforthemodifiedironlossseparationmethodismade.Thus,basedonnumericalcurvefittingthemeasurementresultsofthecorelossesoftheannularamorphousalloyandnanocrystallinecoresundersinusoidalwaves,theanalyticalformulasoftheabovetwomethodsareacquired.Theanalyticalcalculationresultsofthecorelossesofthesetwomethodsarecompared.Finally,themeasuringexperimentofthecorelossesundernon-sinusoidalexcitationfortheannularamorphousalloyandnanocrystallinecoresarecarriedout.Theexperimentalresultsofthecorelossesarecomparedwiththecalculationresultsoftheabovetwomethods,whichverifiestheaccuracyoftheabovetwomethodsundernon-sinusoidalexcitation.
Non-sinusoidalexcitation,coreloss,modifiedironlossseparationmethod,modifiedSteinmetzempiricalformulamethod
2015-06-15改稿日期2015-08-17
TM277
张宁男,1991年生,硕士研究生,研究方向为高频变压器优化设计方法与应用。
E-mail:m15601569550@163.com(通信作者)
李琳男,1962年生,教授,博士生导师,研究方向为电磁场数值计算和电力系统电磁兼容等。
E-mail:ncelilin@aliyun.com
国家电网公司科技项目资助。

