低频叠加PWM波复合励磁下磁心损耗的测量与模型
叶建盈, 陈 为
(1. 福建工程学院信息科学与工程学院, 福建 福州 350118;2. 福州大学电气工程与自动化学院, 福建 福州 350108)
1 引言
功率变换器中磁元件的励磁除了无直流偏磁和直流偏磁下PWM波励磁外,还有低频叠加PWM波复合励磁,包括功率因数校正电路(PFC)电感器的工频整流波叠加PWM波励磁和逆变输出滤波电感上的工频叠加PWM波励磁等,其波形要比其他磁元件励磁的波形复杂,它们的磁化过程比直流滤波电感、功率电感或谐振电感等的磁化过程复杂得多。现有磁心损耗研究的重点基本都集中在研究无直流偏磁和直流偏磁下PWM波励磁的磁心损耗测量和模型[1-6],由于励磁波形的复杂性,高、低频多频叠加工况下磁元件磁心损耗的精确测量和模型建立一直是学术界的难题,业界对此类励磁下的磁心损耗的研究并不多。
文献[7]通过对斯坦麦茨方程SE参数进行修正,以计算功率变换器中磁化过程的连续模式(CCM)和断续模式(DCM)工况下的高频磁心损耗。进一步将两种模式下的模型应用于计算功率因数校正电路中PFC电感的每个高频周期磁心损耗。最后通过取工频周期内每个高频周期磁心损耗的平均值来评估PFC电感的总磁心损耗。
文献[8]认为磁心损耗与磁通密度变化率息息相关,功率变换器中电感的励磁电压大多情况是方波或准方波,因此可将一个开关周期分为磁通密度变化率dB/dt不同的两个阶段,每个阶段的dB/dt保持不变。在此思路上,将整个工频半周期内的磁通密度B(t)波形分为k段(t0~tk),每段内的磁通密度变化率dB/dt不变,从而提出了若干个高频周期内的磁心损耗计算公式,并将该公式应用于SIMPLIS电路仿真软件计算PFC电感的磁心损耗。
文献[9-12]对逆变输出滤波电感的磁心损耗进行了研究,研究的依据都是基于动态磁滞回线的面积可以有效反映磁心损耗的基本思想,共同点都是对电感的动态磁滞回线形状进行分析和研究。由于工频偏磁PWM波励磁工况电感磁心的动态磁滞回线是由许多高频周期的磁滞回线组成,且每个高频周期的动态磁滞回线是非闭合的,因此在计算磁心损耗时,不能简单地引用动态磁滞回线的计算方法。文献[9-12]中将不闭合的动态磁滞回线近似为准闭合的回线,并通过多项式函数对等效面积进行拟合计算,进而计算逆变输出滤波电感的磁心损耗。
文献[13]将逆变输出滤波电感的动态磁滞回线近似为一个磁滞回线。通过计算逆变输出滤波电感在B-H平面上每个高频周期磁通密度和磁场强度的最大值点和最小值点,从而构造两个包络线,并认为包络线之间所包围的每个平行四边形面积是磁心损耗的高频分量,整个包络线中间空白部分为低频分量,通过双包络线法实现了磁心损耗中高频分量的分离。
为了能够有效地对低频叠加PWM波励磁下磁心损耗进行评估,本文首先介绍磁元件动态磁滞回线的测量原理,建立测量多频复合磁心损耗的测量平台;通过深入分析多频复合下的低频和每个高频周期内磁心的励磁和去磁过程,分离出工频和高频分量所对应的损耗,并建立模型;最后通过实验验证了其有效性和准确性。
2 低频叠加PWM波复合励磁下磁心损耗的测量
2.1 动态磁滞回线的测量原理
磁性材料动态磁滞回线的面积代表一个周期内的磁心损耗密度,但是,对于低频叠加高频PWM波复合情况,当低频周期是高频周期的N倍时,一个低频周期的动态磁滞回线不仅包含了N个高频周期过程,也包含了低频周期过程,比单个频率的动态磁滞回线要复杂得多,其动态磁滞回线示意图如图1所示。
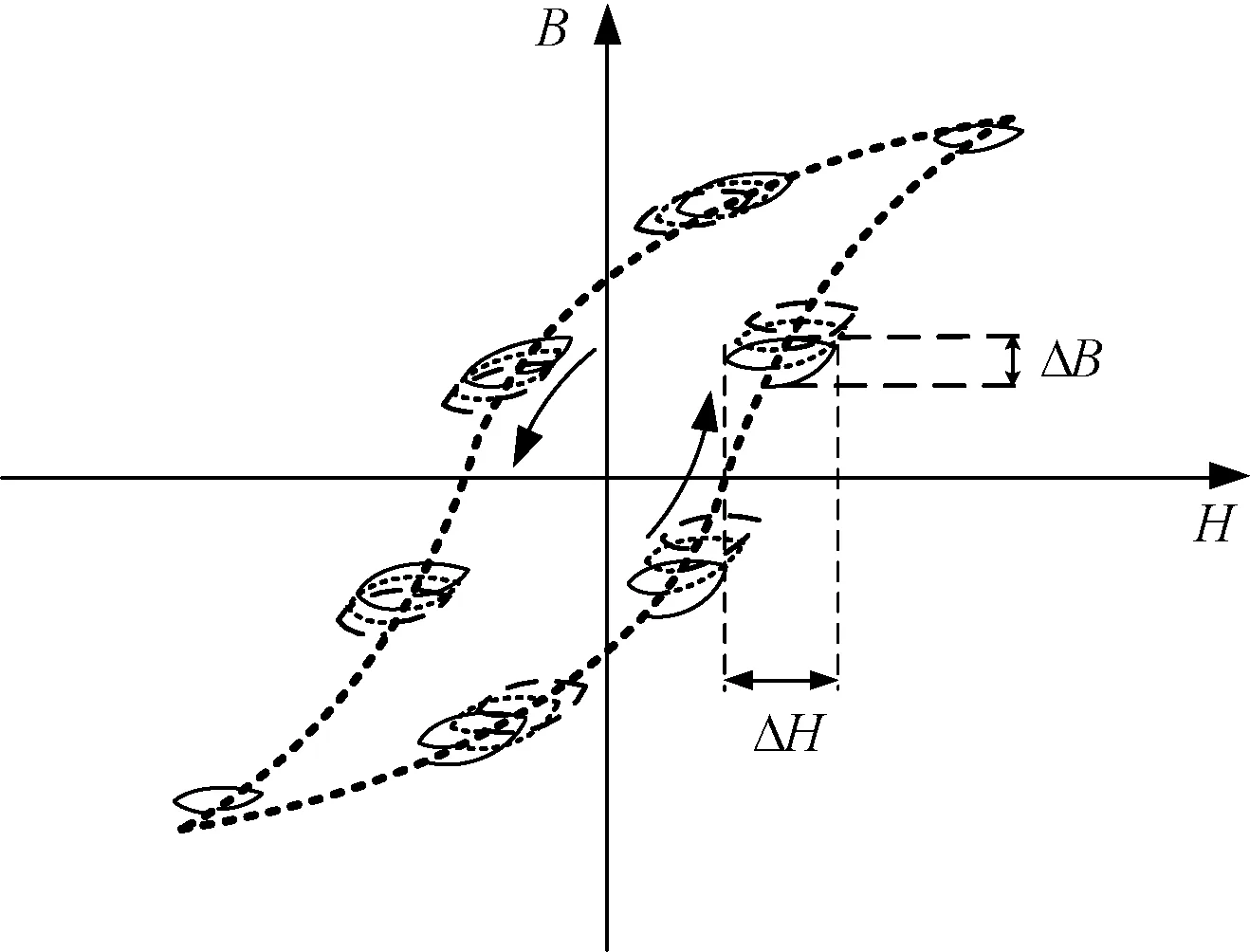
图1 低频叠加PWM波复合下的动态磁滞回线示意图Fig.1 Dynamic hysteresis loop under complex excitation with superimposing of low and high frequency PWM
动态磁滞回线测量磁心损耗的最大特点是可看出磁心损耗在B-H平面的形成过程,以及励磁和去磁过程其形状的变化情况,因此可以根据形成的细节对低频和高频分量进行研究。采用双绕组交流采样法,动态磁滞回线的测量原理如下:采样被测磁元件的二次侧励磁感应电压u2(t)和励磁电流i1(t),再将励磁电压和电流转换为瞬态磁通密度B(t) 和瞬态磁场强度H(t),进而在B-H平面生成动态磁滞回线,然后通过计算一个周期内磁滞回线的平均面积即可得到磁心损耗密度。具体的分析过程如下:
磁化过程磁心损耗的功率表达式为:
(1)
式中,Tg为低频周期。
根据电磁感应定律可得被测磁元件二次侧感应电压为:
(2)
式中,N为被测磁元件的匝数;Ae为磁心横截面积。
再根据安培环路定律可得流经被测磁元件的电流为:
(3)
式中,le为磁心等效磁路长度。
将式(2)和式(3)带入式(1)可得到磁心损耗密度公式为:
(4)
式中,Sall为一个低频周期内动态磁滞回线的总面积;Sk为第k个高频周期的动态磁滞回线面积。
上述的分析和式(4)说明磁心损耗密度为一个低频周期内动态磁滞回线所包围面积的平均值,也就是说,通过测量和计算不同工况下每个动态磁滞回线的面积就可以实现对磁心损耗的测量,同时可以看出每个高频动态磁滞回线的大小和形状的形成过程。因此,本文从动态磁滞回线的角度测量和计算复合励磁工况下的磁心损耗,以便了解多频复合磁化过程和磁心损耗形成的细节。
2.2 复合励磁下磁心损耗的测量电路
为了研究此类高、低频多频叠加励磁下的磁心损耗,设计了测量电路,如图2所示。电路中包含了高频PWM波励磁源电路和低频励磁源电路,通过将这两种励磁叠加并施加到被测磁元件上,实现高频磁通密度和低频磁通密度分量的单独调节和控制。该工况下的低频电压分量往往比较小,为了便于调节幅值大小,低频励磁电源由交流稳压电源和降压变压器组成;高频PWM电源由全桥DC/AC逆变电路组成。
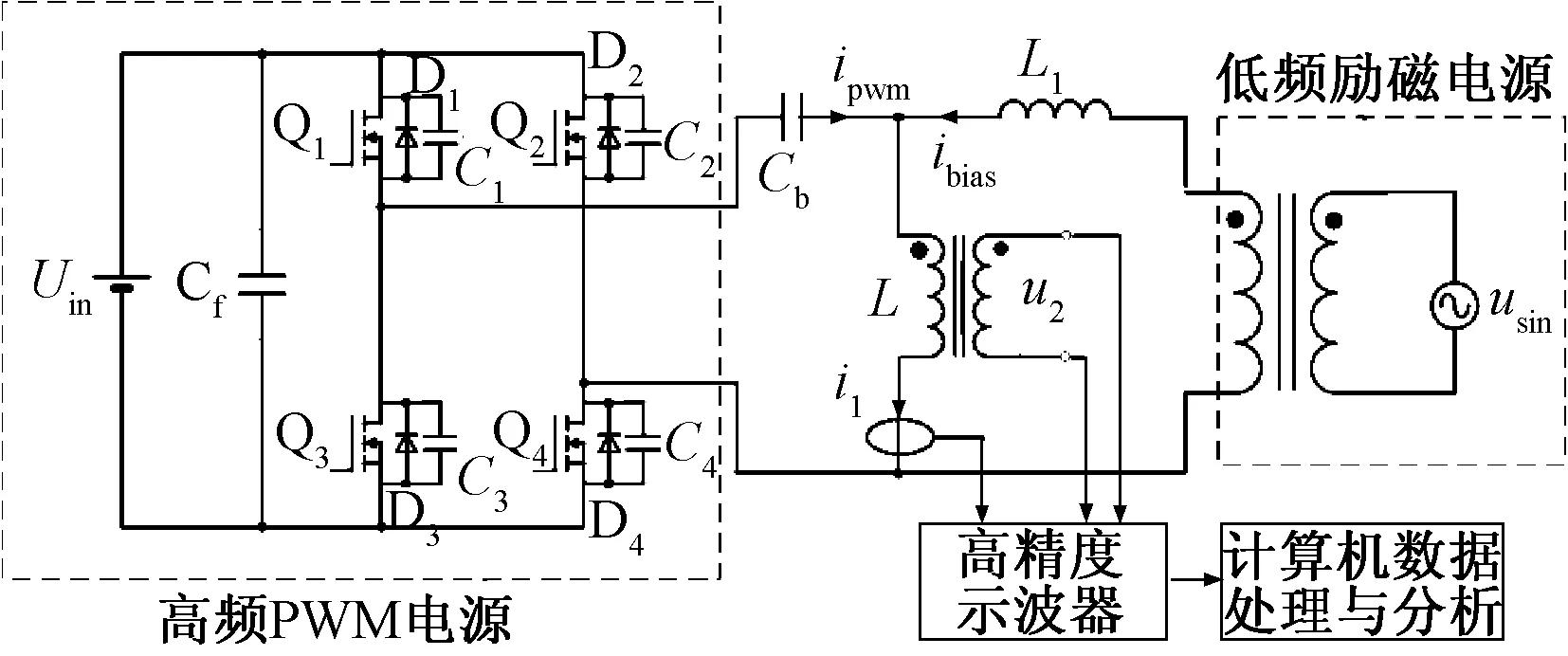
图2 低频叠加高频PWM波励磁的磁心损耗测量原理图Fig.2 Core losses test scheme under complex excitation with superimposing of low and high frequency PWM
图2中,隔直电容Cb阻隔由于逆变桥可能的控制不平衡所引起的直流分量,确保高频PWM电源施加到被测磁元件L上的励磁中无偏磁,同时也对低频电源起隔离作用,以免低频电源影响到高频PWM源;电感L1的主要作用是隔离高频PWM电压使得高频源不会影响到低频源Usin。
磁心损耗的测量通过采用2.1节的动态磁滞回线面积计算法实现。采用高精度数字示波器对被测电感L的励磁电流i1和二次侧感应电压u2进行采样,进一步将采样获得的数据经过计算机处理和计算,将励磁电流和电压转换为瞬态磁场强度H(t)和瞬态磁通密度B(t),并在B-H平面形成动态磁滞回线。则通过计算低频周期内的所有动态磁滞回线的面积可以得到被测磁元件在低频叠加高频PWM波复合励磁下的磁心损耗,同时也可以通过计算每个高频周期内的动态磁滞回线面积获得高频周期内的磁心损耗。
3 磁心损耗低频与高频分量分离的理论分析
由2.1节的测量原理可知,通过计算动态磁滞回线的总面积和高频周期内的面积可获得该工况下的总磁心损耗和每个高频周期内的磁心损耗。但对于低频叠加高频PWM波的励磁,磁滞回线中低频分量和高频分量相互交融和相互影响,为了便于磁元件的分析设计和掌握该工况下磁心损耗的组成成分和变化规律,有必要将高频分量从中分离出来。
通过深入分析发现,根据磁化过程的不同,每个高频周期Ts内的动态磁滞回线的形状和闭合方式有所不同,可以归纳为四种情况:正向励磁过程(第I、IV象限)、反向励磁过程(第II、III象限)、正向去磁过程(第I象限)和反向去磁过程(第III象限)。
(1)正向励磁过程和反向励磁过程
正向励磁过程如图3所示。其中图3(a)为两个高频周期内的动态磁滞回线,可以认为第一个动态磁滞回线A1-B1-C1-D1到第二个动态磁滞回线D1-E1-F1-G1是沿着低频励磁曲线的方向往上走,使得动态磁滞回线不是一个闭合曲线,而是沿着低频磁滞回线的正向励磁曲线方向移动,这个过程低频励磁部分所对应的是磁心储能过程。
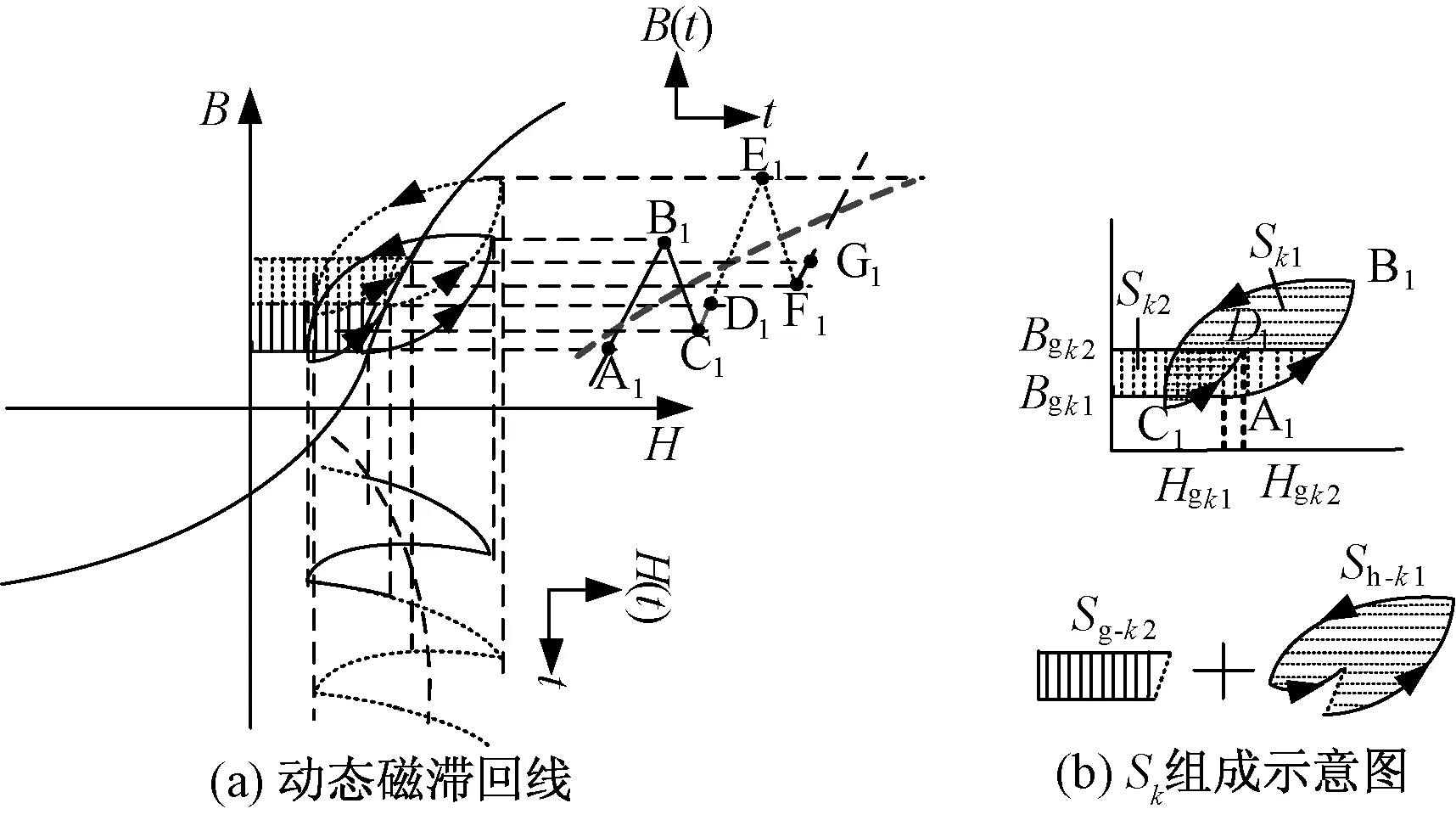
图3 正向励磁过程动态磁滞回线Fig.3 Dynamic hysteresis loop of forward excitation process
每个高频周期Ts内的动态磁滞回线面积Sk的计算公式为:
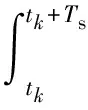
(5)
该面积可以由图3(b)中的Sk1和Sk2两部分面积组成,那么,可以将这两部分面积重新拆分成低频分量Sg-k2和高频分量Sh-k1:
Sk=Sh-k1+Sg-k2
(6)
低频分量面积Sg-k2的计算公式为:
(7)
因此这种情况的高频分量计算公式为:
(8)
反向励磁过程(第II、III象限)与正向励磁过程类似,不同仅在于这个过程磁场强度为负值,其高频计算公式仍采用式(8)。
(2)正向去磁过程和反向去磁过程
正向去磁过程如图4所示。图4(a)为两个高频周期内的动态磁滞回线,可以认为第一个动态磁滞回线A2-B2-C2-D2到第二个动态磁滞回线D2-E2-F2-G2是沿着低频去磁曲线的方向往下走,同样使得动态磁滞回线不是一个闭合曲线,而是沿着低频磁滞回线的正向去磁曲线方向移动,这个过程低频励磁部分所对应的是磁心释放能量过程。
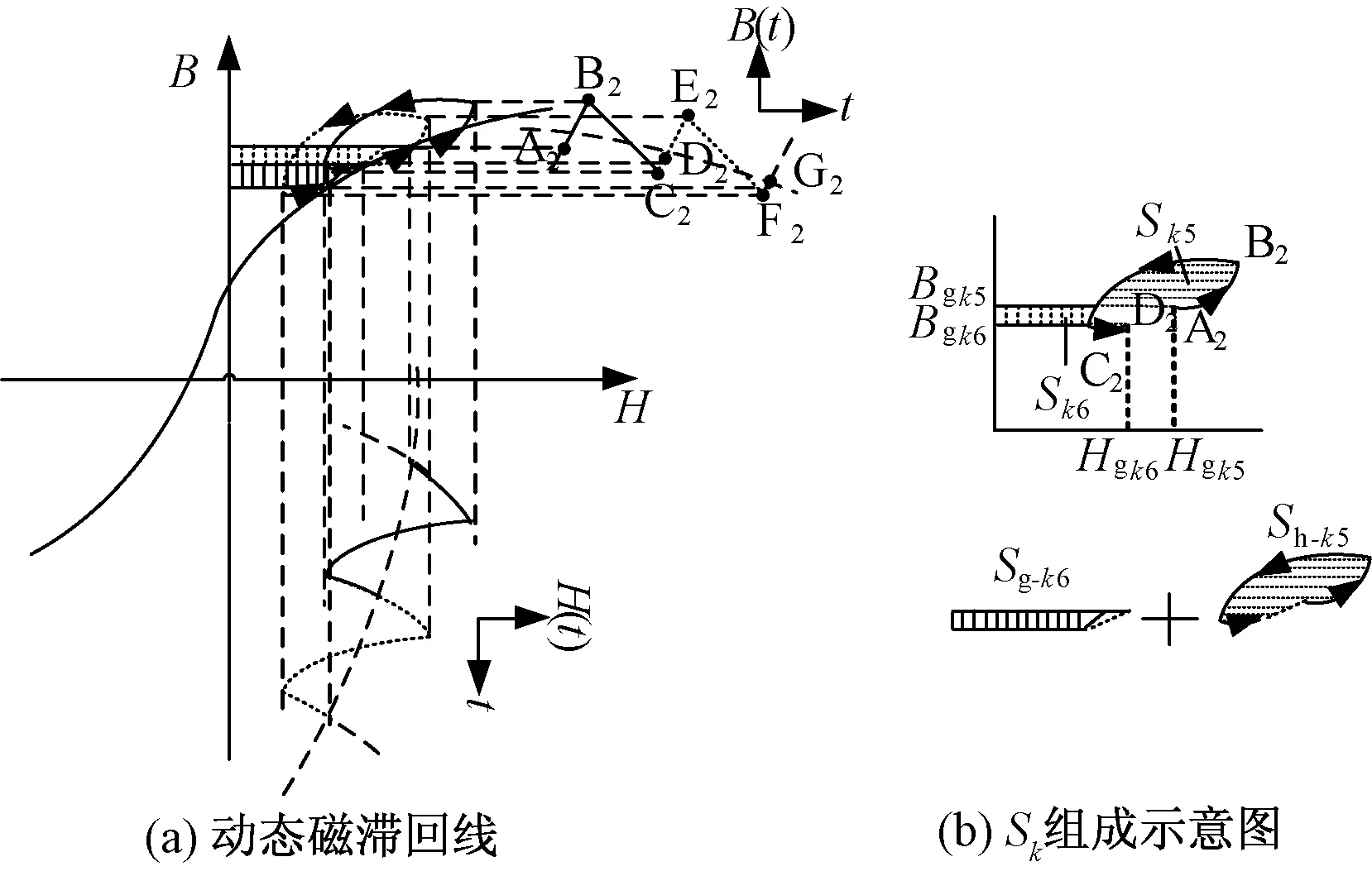
图4 正向去磁过程动态磁滞回线Fig.4 Dynamic hysteresis loop of forward demagnetizing process
根据式(5),可以获得一个高频周期Ts内的面积Sk,且该面积可以由Sk5和Sk6组成,那么,可以将这两部分面积重新拆分成图4(b)中的低频分量Sg-k6和高频分量Sh-k5:
Sk=Sh-k5-Sg-k6
(9)
低频分量的计算公式为:
(10)
因此这种情况的高频分量计算公式为:
(11)
同理,反向去磁过程(第III象限)与正向去磁过程类似,不同仅在于这个过程磁场强度为负值,其高频计算公式仍采用式(11)。
综上所述,通过式(8)或式(11)就可将低频叠加PWM波复合励磁下每个高频周期磁心损耗中的高频分量和低频分量进行分离,因此通过该计算方法可以很清楚地了解每个高频周期内磁心损耗的分布情况,为进一步分析该工况下的磁心损耗提供理论基础。
4 磁心损耗低频与高频分量分离的实验
根据第3节分析的低频和高频磁心损耗分离方法,对该工况下磁心损耗进行测量,通过实验手段将该工况下每个高频周期中的磁心损耗的高频和低频分量分离出来,为后续的模型建立提供基础。
根据图2搭建了磁心损耗测量平台,对TP4(生产厂商:浙江天通电子股份有限公司)环形铁氧体磁心在低频叠加高频PWM波复合励磁下的损耗进行测量,磁心的尺寸参数具体见表1。绕组采用100×φ0.1mm 厘兹线,匝数为25。复合励磁源中低频励磁采用频率和交流磁通密度分别为50Hz和0.3T的正弦波励磁,高频PWM励磁采用频率和交流磁通密度分别为20kHz和0.1T的方波励磁。

表1 铁氧体TP4磁心参数Tab.1 Core parameters of Ferrite TP4
图5为被测电感的励磁电流i1(t)和二次侧绕组的感应电压u2(t)。将u2(t)和i1(t)两采样值通过计算和处理得到瞬态磁通密度B(t)和瞬态磁心磁场强度H(t)。
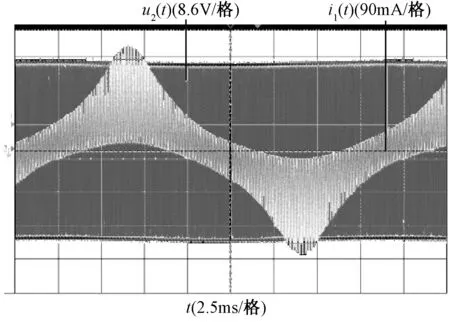
图5 工频偏磁PWM波励磁下的电压和电流波形Fig.5 Voltage and current waveforms of power frequency bias
将磁场强度H(t)和磁通密度B(t)应用于B-H平面可得到工频周期Tg内的动态磁滞回线,如图6所示。该回线由N=Tg/Ts个高频动态磁滞回线组成且形成一个闭合的曲线。图7为不同高频周期动态磁滞回线和局部放大图。为了便于观察,只列出四组动态磁滞回线,每组由两个动态磁滞回线组成。可以看出,不同的磁场强度H(t)在高频周期Ts内的高频动态磁滞回线形状和面积都是不同的,即将工频偏磁N等分后,在不同的工频偏磁位置磁心损耗都是不相同的。图7右边部分为工频正向励磁过程的单个高频动态磁滞回线,可以看出高频周期内磁滞回线在磁化过程形成的细节,而且形成的是非闭合的曲线,这与第3节的正向励磁过程的理论分析是一致的,说明了本文计算方法可以通过实验的手段对磁心损耗的工频和高频分量进行分离。
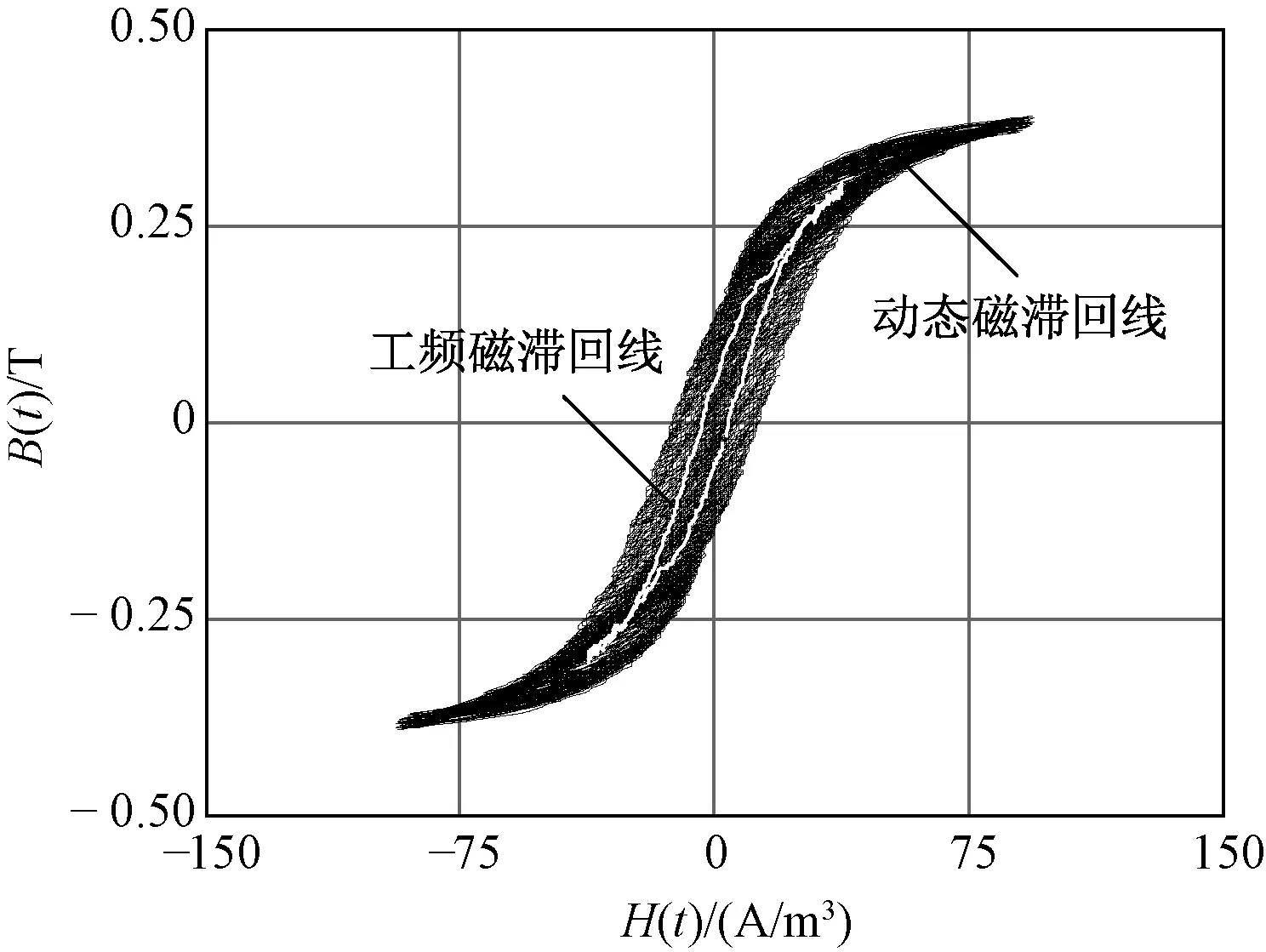
图6 工频偏磁下的动态磁滞回线Fig.6 Dynamic hysteresis loop of power frequency bias
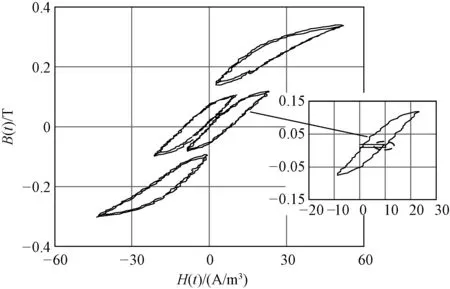
图7 不同高频周期动态磁滞回线和局部放大图Fig.7 Dynamic hysteresis loop and local enlarged drawing of different high frequency cycles
图8为各个高频周期动态磁滞回线面积的波形图。根据式(5)可得到一个工频周期内N个高频周期的动态磁滞回线面积(见图8中Sk波形),Sk反映了工频周期内的磁心损耗变化规律;根据式(7)或式(10)可以得到工频周期N等分后每个周期的工频分量面积(见图8中Sg-k波形),Sg-k为第k个高频周期的工频分量所对应的面积,体现了每个高频周期内工频分量在磁心中的能量存储和释放情况,正值表示外部电路往磁心存储能量,负值表示磁心对外部电路释放能量。根据式(8)或式(11)则可以得到每个高频周期内磁心损耗的高频分量(见图8中Sh-k波形),Sh-k为第k个高频周期的高频分量所对应的面积。可见工频叠加高频PWM波复合励磁下磁元件磁心损耗的高频分量的变化趋势与正弦波的变化趋势相当,但是形状略不同,且工频分量相比于高频分量相对比较小,因此工频对磁心损耗的影响主要体现在每个高频周期内偏磁的不同引起高频磁心损耗的不同。
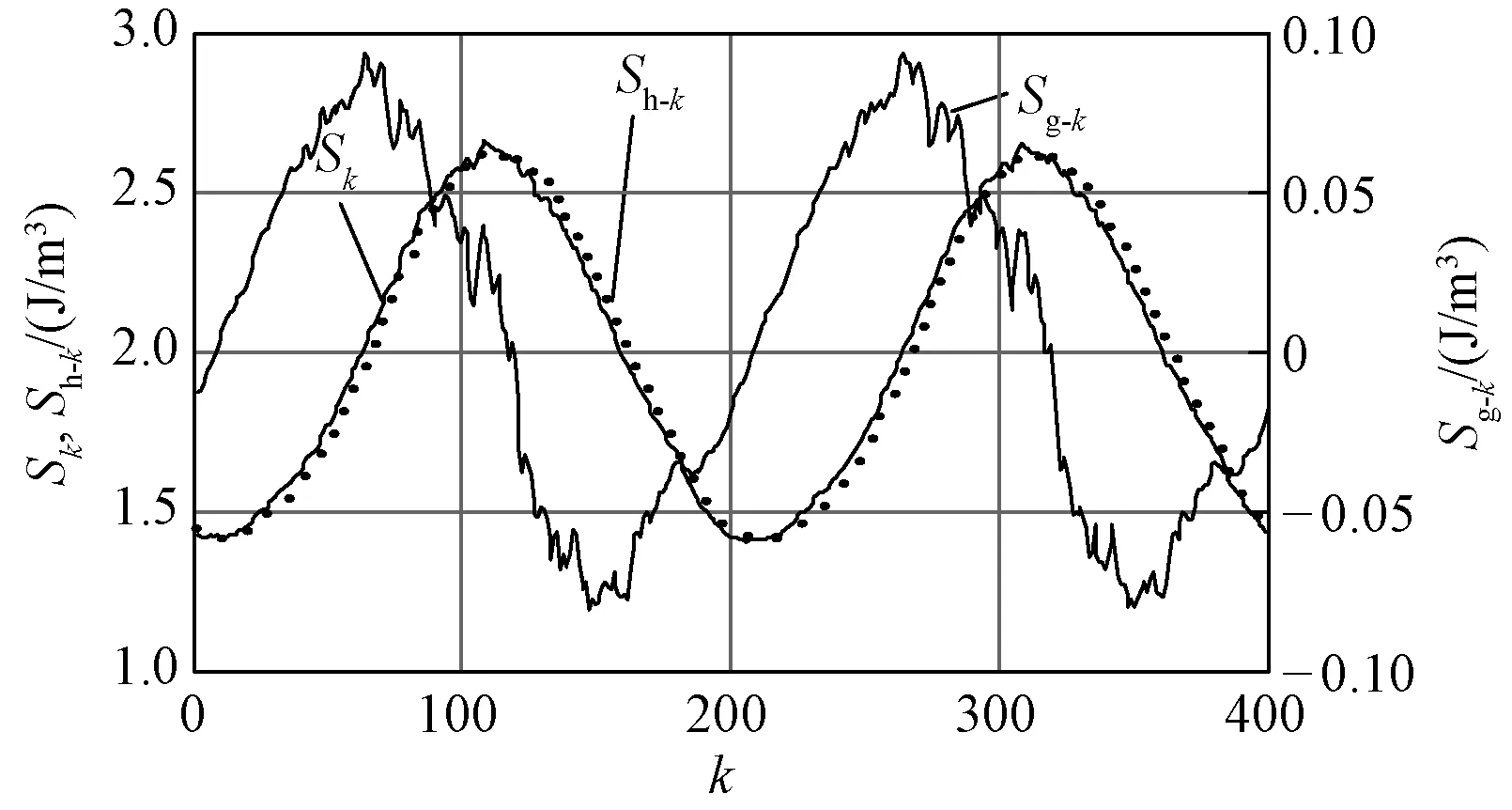
图8 各个高频周期动态磁滞回线面积Fig.8 Area of dynamic hysteresis loop with different high frequency cycles
因此,通过动态磁滞回线测量原理和高频、低频磁心损耗的分离方法,可以有效地实现低频叠加高频PWM波复合励磁下磁元件磁心损耗的低频和高频分量的分离。
5 磁心损耗中高频分量的建模与验证
将低频电压叠加PWM波复合励磁中的低频部分当作低频偏磁处理,并将低频偏磁N等分分布到每个高频周期中,由于高频分量的频率远远大于低频偏磁的频率,那么每个高频周期内的低频偏磁可以近似认为不变,如图9所示。则每个周期内高频分量的磁心损耗可以认为是对应不同直流偏磁工况下的磁心损耗。
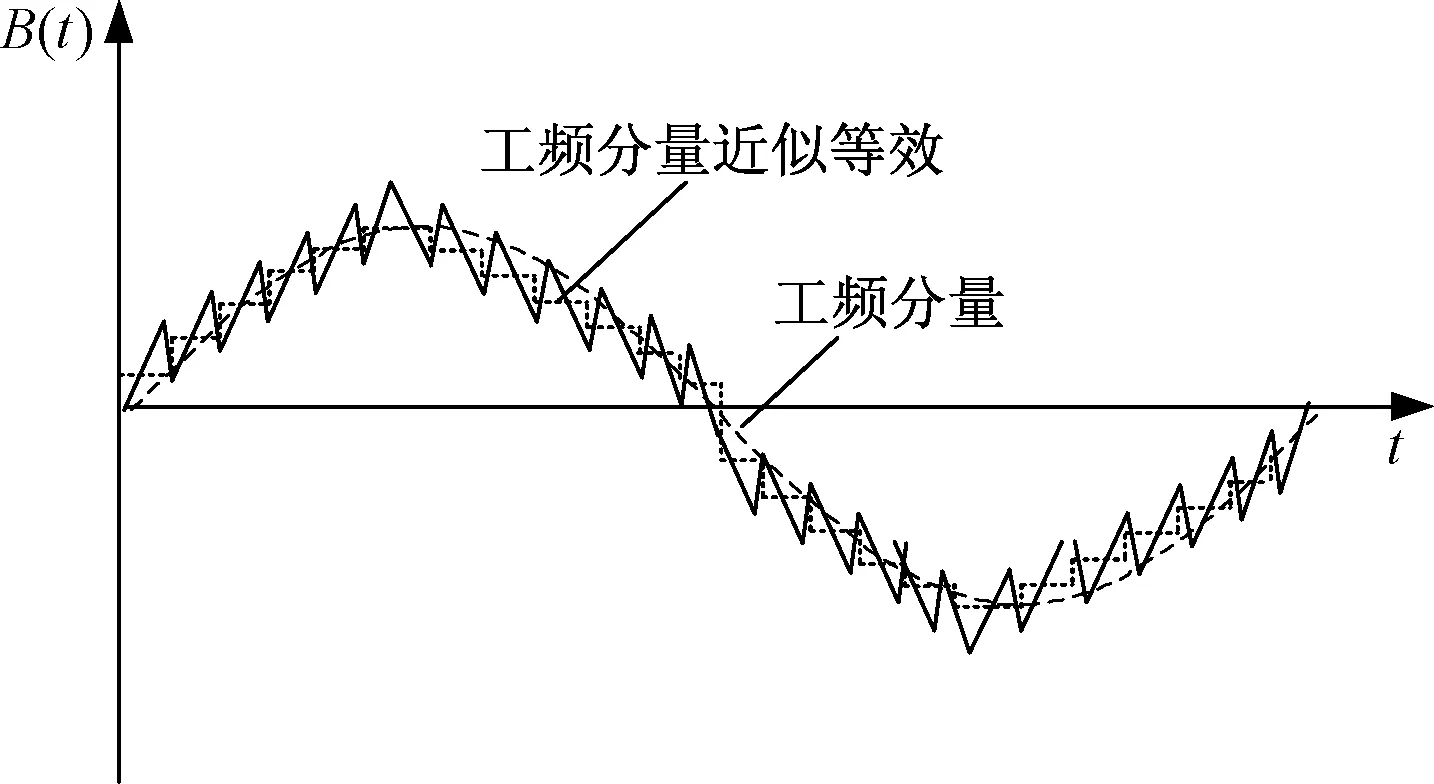
图9 工频偏磁的近似等效Fig.9 Approximate equivalent waveform of power frequency bias
将文献[6]提出的直流偏磁下的磁心损耗模型应用在该工况下磁心损耗的计算,可获得模型为:
(12)
(13)
式中,k为低频叠加PWM波复合励磁下的高频周期数;Hg(k)为第k周期的工频偏磁;Bm为高频磁通密度分量;Ppwm-nb为无偏磁工况下磁心损耗;k1、k2、κ1、κ2、δ1、δ2、α、β分别为该材料的磁心损耗参数。
低频周期内磁心损耗高频分量的总损耗为:
(14)
由动态磁滞回线测量原理可知,获得的高频磁心损耗分量的计算结果为面积,为了便于模型的验证和对比,进一步将式(12)磁心损耗的模型转换为面积的公式:
Sh(k)=TsPcv(k)
(15)
式中,Ts为高频周期。
首先,对TP4磁心材料在直流偏磁下占空比为0.5的PWM波励磁的磁心损耗进行测量,并将测量结果与直流偏磁工况下的模型式(12)进行拟合,可以获得直流偏磁下磁心损耗模型的拟合系数:k1=0.19,k2=1.78×10-5,α=1.946,β=2.48,κ1=0.3501,κ2=6.0181,δ1=0.8248,δ2=0.6729。因此,通过这些系数和式(12)或式(14)就可以计算出低频周期内的每个高频周期的磁心损耗高频分量。
然后,测量低频叠加PWM波复合励磁下的磁心损耗。复合励磁源中低频励磁采用频率和交流磁通密度分别为50Hz和0.25T的正弦波励磁,高频PWM励磁采用频率为20kHz的方波,交流磁通密度的峰值Bm分别为0.06T、0.08T 和0.1T。通过实验和模型式(14)的计算可得到Bm为0.08T时每个高频周期的磁心损耗高频分量对比图,如图10所示。
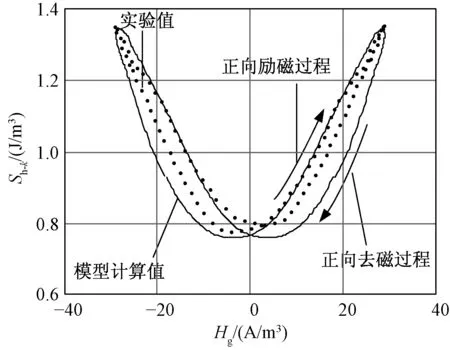
图10 工频周期内的高频分量实验值与模型值的比较Fig.10 Comparison between model calculation and measurement for high-frequency component with power cycle
可以看出,实验值和模型值比较接近,都能有效地反映在磁化过程的磁心损耗高频分量的变化情况,正向励磁和去磁过程的磁心损耗与反向励磁和去磁过程的磁心损耗高频分量是对称的,且励磁过程和去磁过程的高频分量磁心损耗略有不同。
最后,对该工况下工频周期内磁心损耗高频分量的总损耗进行对比验证。表2为上述励磁下的磁心损耗实验值和模型计算值的数据。可以看出,磁通密度工频分量对磁心损耗具有一定的影响,所提出的模型能够有效地地评估预测工频叠加PWM波复合励磁下磁心损耗的高频分量。
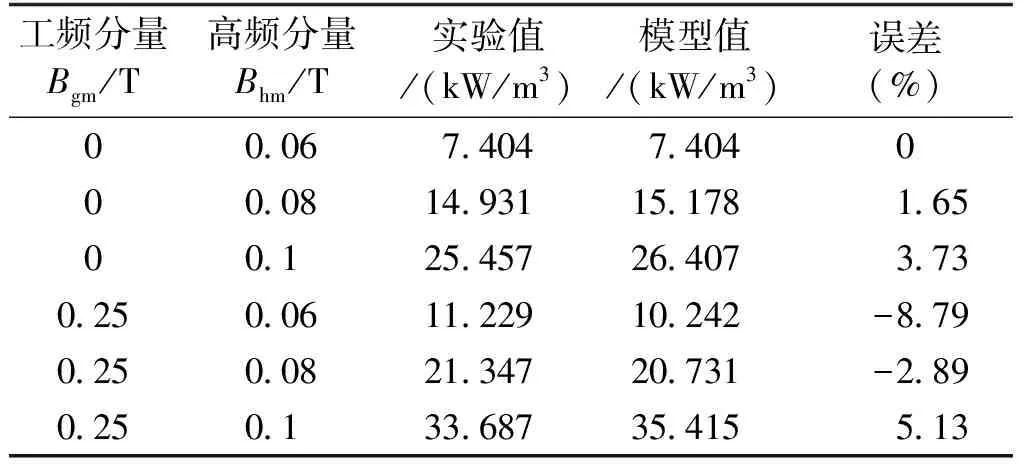
表2 复合励磁下磁心损耗高频分量的实验值和模型值Tab.2 Model calculation and measurement for high-frequency component with complex excitation
综上所述,磁通密度低频分量对磁心损耗的影响不可忽视,本文提出的高频模型不仅足以准确评估该励磁下磁心损耗的总高频分量,还可以很好地评估每个高频周期内磁心损耗的高频分量。另外,磁心损耗的低频分量可通过形式简单的斯坦麦茨方程SE模型计算得到。因此,高频、低频磁心损耗分量的分离方法和高频模型的建立可以为该工况下磁元件损耗的优化设计提供有效的手段。
6 结论
(1)介绍和分析了动态磁滞回线测量磁心损耗的测量原理,设计了低频叠加PWM波复合励磁下磁心损耗的测量电路,并建立了基于动态磁滞回线测量磁心损耗的测量装置,可以实现不同磁通密度高频分量和低频分量下磁心损耗的测量。
(2) 对复合励磁下磁心的动态磁滞回线进行深入分析和研究,提出了磁心损耗的高频和低频分量的分离方法,进一步提出了高频和低频分量的计算公式,并通过实验获得了该工况下磁心损耗的低频和高频分量值。
(3)利用直流偏磁下PWM波励磁的磁心损耗模型,将其应用到低频周期内每个高频周期的损耗计算,得到了复合励磁下磁心损耗的高频分量模型,并通过实验验证了模型的可行性和精度。
(4) 磁心损耗高频和低频分量的分离方法以及高频模型可用于评估不同工况下PFC电感和逆变输出滤波电感的磁心损耗,也可用于优化不同控制策略下PFC电感和逆变输出滤波电感的磁心损耗。
(5) 本文提出的模型参数较少,对功率变换器中磁元件磁心损耗在工程分析和设计的应用具有一定价值。
[1] 汪晶慧,陈为(Wang Jinghui,Chen Wei).超低损耗角磁心高频损耗测量方法(High frequency core loss measurement of low loss angle magnetic component)[J].电工技术学报(Transactions of China Electrotechnical Society),2012,27(11):133-138.
[2] 汪晶慧,陈为(Wang Jinghui,Chen Wei).超低损耗角磁芯损耗测量的量热计法(Study of calorimetric method to measure loss of super low loss angle core) [J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2012,31(4):6-9.
[3] Tan F Dong, Vollin J L, Cuk S M. A practical approach for magnetic core-loss characterization[J].IEEE Transactions on Power Electronics, 1995, 10(2): 124-130.
[4] Shen W, Wang F, Boroyevich D, et al.Loss characterization and calculation of nanocrystalline cores for high-frequency[J]. IEEE Transactions on Power Electronics, 2008, 23(1): 475-484.
[5] Mu Mingkai.High frequency magnetic core loss study[D].Virginia:Virginia Polytechnic Institute and State University,2013.
[6] 叶建盈,陈为,汪晶慧(Ye Jianying, Chen Wei,Wang Jinghui).PWM 波及直流偏磁励磁下磁芯损耗模型研究(Research on the core loss model under PWM wave and DC bias excitations)[J].中国电机工程学报(Proceedings of the CSEE),2015, 35(10):2601-2606.
[7] Larouci C, Ferrieux J P, Gerbaud L, et al. Experimental evaluation of the core losses in the magnetic components used in PFC converters: Application to optimize the flyback structure losses[A].Applied Power Electronics Conference and Exposition[C].2002. 326-331.
[8] Liu Jinjun,Wilson T G,Wong R C,et al. A method for inductor core loss estimation in power factor correction applications[A].Applied Power Electronics Conference and Exposition[C]. 2002. 439-445.
[9] Iyasu S,Shimizu T,Ishii K.A novel iron loss calculation method on power converters based on dynamic minor loop[A].European Conference on Power Electronics and Application[C].2005. 9-10.
[10] Toshihisa Shimizu, Seiji Iyasu.A practical iron loss calculation for AC filter inductors used in PWM inverters[J].IEEE Transactions on Industrial Electronics, 2009,56(7): 2600-2609.
[11] Shimizu T,Kakazu K,Takano K,et al.Loss evaluation of AC filter inductor core on a PWM converter[A].IEEE 8th International Conference on Power Electronics and ECCE Asia[C].2011. 1047-1052.
[12] Kwanryol K,Shimizu T,Takano K,et al.Dynamic iron loss measurement method for an AC filter inductor on a PWM inverter[A]. European Conference on Power Electronics and Applications[C].2007 . 1-9.
[13] Ma Jiong, Liu Hongyang, Ma Hao, et al. A novel hysteresis loss calculation method of filter inductor in PWM inverters[A].39th Annual Conference of the IEEE Industrial Electronics Society[C].2013. 287-292.

