高频电子电路用圆形截面环形磁心中电磁场的分布
田莉,田铭兴
(兰州交通大学自动化与电气工程学院,甘肃兰州730070)
高频电子电路用圆形截面环形磁心中电磁场的分布
田莉,田铭兴
(兰州交通大学自动化与电气工程学院,甘肃兰州730070)
为了研究当线圈缠绕于高频电子电路用圆形截面环形磁心某一段,考虑漏磁时磁心内部电磁场的分布,根据磁通连续性原理及镜像法,将绕有一个线圈的环形磁心内电磁场的分布问题,转化为绕有无穷多个线圈的无限长直磁心在其中一段磁心内的电磁场分布问题。基于麦克斯韦方程组和叠加原理,推导了环形磁心内电场强度和磁场强度的单重级数式解析计算公式。基于电场强度的计算公式,得到了涡流损耗的计算公式,与基于线圈自阻抗得到的涡流损耗计算公式进行对比,二者的计算结果吻合良好,证明了本文分析方法及所得公式的正确性。电场强度和磁场强度的计算结果分析表明,本文结论也同样适用于磁心磁导率很高或线圈均匀密绕于磁心表面,即漏磁通很小可以忽略的情况。
环形磁心;电磁场分布;解析解;贝塞尔函数
1 引言
构成变压器和传感器等磁性器件的环形磁心在电子电路中大量使用[1],随着激励频率的增大,其内部电磁场的分布及其损耗受到了越来越多的关注[2-8]。文献[2]分析了变压器三种常用磁心材料即铁氧体、纳米晶和非晶材料的损耗特性与频率、磁通密度的关系,并给出了磁性材料损耗密度的三维表征图。文献[3]用有限元法对环形磁心内的磁场分布进行了数值计算,并计算了涡流损耗。文献[4,5]研究了螺线管线圈在矩形截面环形磁心中的磁场分布及涡流损耗,并给出了解析解。文献[6,7]研究了螺线管线圈在圆形截面环形磁心中的电场磁场分布及其铁耗,给出了解析解。但文献[4-7]的求解过程都是假设螺线管线圈均匀密绕于磁心表面上,或磁心的导磁率很大,即不考虑漏磁通时得到的。
本文研究的磁件结构如图1所示,线圈缠绕于部分磁心之上。图1中,环形磁心的截面为圆形,半径为b,磁心中心线长l;磁心材料为各向同性的线性媒质,电导率为σ,磁导率为μ2;线圈的匝数为N,截面为矩形,长h,宽w。显然,在分析这种情况下磁心内的电磁场及损耗时,其漏磁通就不应忽略。

图1 绕有线圈的环形磁心Fig.1Toroidal cores encircled by coil
为了研究图1磁件磁心内电磁场的分布,将其磁心切开,展成直磁心,两端为电导率为0、磁导率无穷大的无限大线性媒质,保证了磁通的连续性。基于镜像法和叠加原理,得到了图1磁件考虑漏磁通时磁心内电场强度和磁场强度的级数式解析计算公式。
2 单匝细线圈绕于圆形截面无限长直磁心上时磁心内的电场强度
无限长直磁心上绕有单匝细线圈的情况如图2所示。磁心外为空气,磁导率为μ1;磁心磁导率及半径同图1;线圈通以电流=。

图2 无限长磁心上绕单匝细线圈Fig.2Infinite long cores encircled by filamentary turn

式中,I1、K1、I0、K0为修正的一阶和零阶Bessel函数;
对式(1)进行积分反变换并整理得


为了书写方便,将式(3)写为

3 单匝细线圈绕于圆形截面环形磁心上时磁心内的电场强度
磁件结构同图1,线圈为单匝细线圈,其参数同图2中的线圈。考虑到实际中磁心一般有l/b>25[9],忽略内外径的差别,将磁心在A-A'切开,展开成长度为l的直磁心,磁心两端为磁导率无穷大而电导率为0(μ=∞,σ=0)的无限大线性媒质。由镜像法可知,位于两无限大平行边界之间的电流在该区域中形成的场,由该电流形成的场和两个无限大平行平面镜像的无数个电流所形成的场叠加而成。展开的环形磁心及镜像线圈如图3所示。

图3 展开的环形磁心及镜像线圈Fig.3Opening toroidal cores and turn mirror image
式(4)为实际线圈电流在磁心(r,z)处形成的电场强度,将所有线圈在(r,z)处产生的电场强度叠加可得环形磁心内的电场强度

根据冲击函数的傅里叶级数展开公式

式中

当k=0时,βk→0,依据Bessel函数在变量趋于0时的渐近线公式,得到式(8)k=0项的值为

式中,μ2r为磁心的相对磁导率,μ2r=μ2/μ1。
因此,式(8)可写为如下形式式中

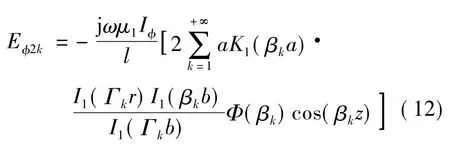
4 N匝细线圈绕于圆形截面环形磁心上时磁心内的电磁场
对图1所示磁件结构,圆形截面环形磁心上绕了N匝线圈,如果忽略匝间隙,则单位面积的匝数为,面积元ds内的匝数为,则磁心中面积元ds内的线圈在磁心(r,z)处产生的电场强度为


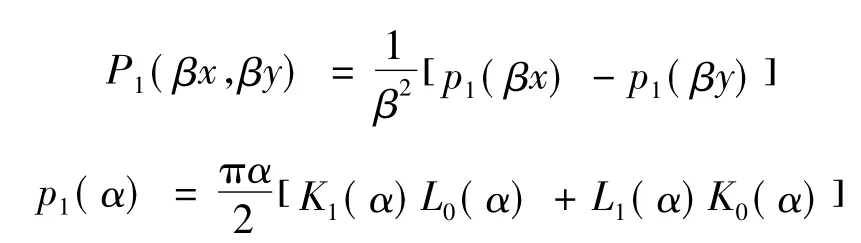
其中,L0(x)、L1(x)分别为零阶和一阶修正的Struve函数。

磁场强度z方向的分量Hz为
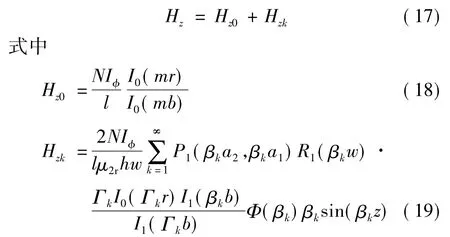
5 结论验证

另外,绕在磁心上的线圈自阻抗的实部是表征涡流损耗的一个等效参数[10]。所以,为了在算例中比较验证式(20)的正确性,这里给出另外一个涡流损耗平均功率的计算公式
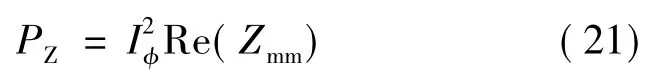
式中,Zmm是由文献[8]得到的绕有线圈的环形磁心中的磁通引起的线圈自阻抗,其计算公式为

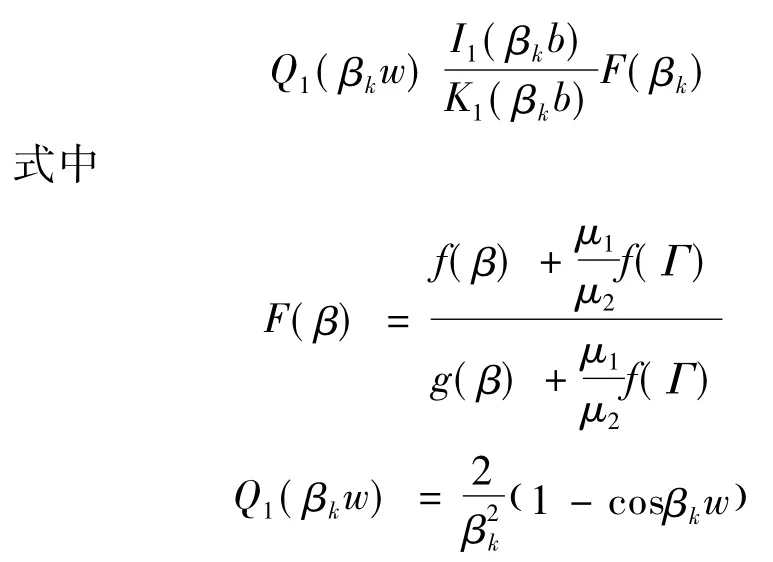
对图1所示的磁件结构,采用文献[9]算例中的磁心及载流线圈参数,磁心参数如下:磁路长度l =250mm,磁心半径b=10.8mm,相对磁导率μ2r= 75,磁心电导率σ=100S·m-1;线圈参数如下:NI= 25A,w=10mm,h=10mm,a1=15mm,a2=25mm。按式(20)和式(21)对该环形磁心内的涡流损耗进行实际计算,结果如表1所示,两个公式的计算结果吻合良好。

表1 涡流损耗平均功率两种计算结果比较Tab.1Comparison of results from Eqs.(20)and Eqs.(21)
6 电磁场的计算分析
6.1 磁导率较低时磁心内电磁场的分布
图1所示磁件,磁心及线圈参数同第5节,磁心内电场强度和磁场强度的分布见图4~图9。其中图4~图6为f=100kHz时电场强度和磁场强度的分布图,图7~图9为f=1MHz时电场强度和磁场强度的分布图。

图4 f=100kHz时|E|的分布Fig.4Distribution of|E|at f=100kHz

图5 f=100kHz时|Hr|的分布Fig.5Distribution of|Hr|at f=100kHz

图6 f=100kHz时|Hz|的分布Fig.6Distribution of|Hz|at f=100kHz

图7 f=1MHz时||的分布Fig.7Distribution of||at f=1MHz
从图4~图9可以看出,电场强度和磁场强度都随r的增大而增大,呈现集肤效应现象;||、|Hz|随z的增大而减小,这是由漏磁通引起,说明这种情况漏磁不能忽略;|Hr|远远小于|Hz|;电场强度随频率的增大而迅速增大。
6.2 当磁心磁导率很高或线圈均匀密绕于磁心表面时磁心内电磁场随z的变化
(1)当磁心磁导率很高时磁心内电磁场随z的变化

图8 f=1MHz时|Hr|的分布Fig.8Distribution of|Hr|at f=1MHz

图9 f=1MHz时|Hz|的分布Fig.9Distribution of|Hz|at f=1MHz
图1所示磁件,磁心和绕组其他参数同第5节,但磁心相对磁导率μ2r=105。计算了r=10mm,f= 1MHz时不同z处电场强度和磁场强度的值,结果见表2和表3。

表2 磁心磁导率很高时电场强度随z的变化Tab.2Variation of electrical field intensity with z when magnetic permeability of core being very high

表3 磁心磁导率很高时磁场强度随z的变化Tab.3Variation of magnetic field intensity with z when magnetic permeability of core being very high
(2)当线圈均匀密绕于磁心表面时磁心内电磁场随z的变化
图1所示磁件,磁心参数同第5节,绕组参数NI=25A不变,因线圈均匀密绕于磁心表面,因此线圈宽度w=l=250mm,a1=b=10.8mm,设h= 1mm,则a2=11.8mm。计算r=10mm,f=1MHz时不同z处电场强度和磁场强度的值,计算结果见表4和表5。

表4 线圈均匀密绕于磁心表面时电场强度随z的变化Tab.4Variation of electrical field intensity with z when core being encircled tightly and uniformly by coil

表5 线圈均匀密绕于磁心表面时磁场强度随z的变化Tab.5Variation of magnetic field intensity with z when core being encircled tightly and uniformly by coil
从表2~表5可以看出,当磁导率很高或线圈均匀密绕于磁心表面时|E|≈|E0|,|Hz|≈|Hz0|,而|Ek|、|Hzk|、|Hr|很小,可以忽略。因此,磁导率很大或线圈均匀密绕于磁心表面时,为本文所研究的特殊情况。
7 结论
(1)推导了绕有线圈的环形磁心,考虑漏磁时其内部电场强度和磁场强度的级数式解析计算公式,基于电场强度的计算公式,得到了涡流损耗的解析解。
(2)公式中不仅包含了磁心的尺寸、磁导率、电导率及线圈的电流、频率、匝数等参数,也包含了线圈的尺寸。因此,给这类磁件的设计提供了依据,具有一定的实用价值。
(3)本文所得电场强度、磁场强度及涡流损耗的计算公式不仅适用于线圈缠绕于部分磁心之上,考虑漏磁的情况;也适用于磁心磁导率很高或线圈均匀密绕于磁心表面,漏磁通很小可以忽略的情况。
参考文献(References):
[1]王兆安,张明勋(Wang Zhao’an,Zhang Mingxun).电力电子设备设计和应用手册(Power electronic devices and application manual)[M].北京:机械工业出版社(Beijing:China Machine Press),2002.
[2]韩帅,张黎,谭兴国(Han Shuai,Zhang Li,Tan Xingguo).基于损耗分析的大容量高频变压器铁芯材料选型方法(Material selection based on loss characterization for high-power high-frequency transformer cores)[J].高电压技术(High Voltage Engineering),2012,38 (6):1486-1491.
[3]应柏青(Ying Baiqing).高频电子电路用圆环形磁芯中涡流损耗的有限元计算(FEM solutions of eddy-current power loss in toroidal cores with arhitray cross section)[J].微电子学与计算机(Microelectronics&Computer),2002,(4):51-53.
[4]K V Namjoshi,J D Lavers,P P Biringer.Eddy current power loss in toroidal cores with rectangular cross section[J].IEEE Transactions on Magnetics,1988,34(3): 636-641.
[5]马西奎,赵彦珍,戴东(Ma Xikui,Zhao Yanzhen,Dai Dong).高频电子电路用矩形截面圆环磁芯中涡流损耗的解析解(Analytical solution of eddy-current power loss in toroidal cores with rectangular cross section for high-frequency electronic circuits)[J].中国电机工程学报(Proceedings of the CSEE),2005,25(6):124-128.
[6]Saotome H,Sakaki Y.Iron loss analysis of Mn-Zn ferrite cores[J].IEEE Transactions on Magnetics,1997,33 (1):728-734.
[7]Daming Zhang,Chek Fok Foo.Theoretical analysis of the electrical and magnetic field distributions in a toroidal core with circular cross section[J].IEEE Transactions on Magnetics,1999,35(3):1924-1931.
[8]Wilcox D J,Conlon M,Hurley W G.Calculation of self and mutual impedances for coils on ferromagnetic cores[J].IEE Proceedings,1988,135(7):470-476.
[9]William G Hurley,David J Wilcox.Calculation of leakage inductance in transformer windings[J].IEEE Transactions on Power Electronics,1994,9(1):121-126.
[10]W M Gerard Hurley,David J Wilcox.Calculation of short circuit impedance and leakage impedance in transformer windings[A].Power Electronics Specialists Conference,PESC’91 Record,22nd Annual IEEE[C].1991.651-658.
Electrical and magnetic field distributions in toroidal core with circular cross section for high-frequency electronic circuits
TIAN Li,TIAN Ming-xing
(Institute of Automatic and Electrical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
In order to study electrical and magnetic field distributions in toroidal core with circular cross section for high-frequency electronic circuits,when it is encircled partly by coil and leakage flux can not be ignored,according to magnetic flux continuity principle and mirror image method,electrical and magnetic field distributions in toroidal cores encircled by one coil are transformed into electrical and magnetic field distributions in the actual section of an infinite long cores along which an infinite number of images are introduced.Based on Maxwell equations and superposition principle,analytical solutions are derived for the electrical and magnetic field intensity,in which the field variables are expressed as a single series in terms of Bessel functions and trigonometric functions.Two analytical solutions of eddy-current power loss are derived.One is based on electric field intensity and the other is based on self impedance.Calculation results agree with each other,and it validates the accuracy and validity of analytical method.Calculation results of electrical and magnetic field intensity show that the conclusion of this paper can be applied to the case of magnetic permeability of core being very high or the core being encircled tightly and uniformly by coil,in which leakage flux can be ignored.
toroidal cores;electrical and magnetic field distributions;analytical solution;Bessel function
TM554
A
1003-3076(2014)10-0033-06
2013-03-12
国家自然科学基金资助项目(51167009)
田莉(1971-),女,甘肃籍,讲师,硕士,研究方向为电机设计及控制;田铭兴(1968-),男,甘肃籍,教授,博士,研究方向为电机电器的设计及控制。

