用于变电站噪声有源控制的一种算法研究
赵宏飞,马宏忠,陈楷,王春宁,钟钦
(1.河海大学能源与电气学院,江苏南京211100;2.江苏省电力公司检修分公司扬州分部,江苏扬州225000;3.江苏省电力公司南京供电公司,江苏南京210008)
用于变电站噪声有源控制的一种算法研究
赵宏飞1,2,马宏忠1,陈楷3,王春宁3,钟钦1
(1.河海大学能源与电气学院,江苏南京211100;2.江苏省电力公司检修分公司扬州分部,江苏扬州225000;3.江苏省电力公司南京供电公司,江苏南京210008)
随着城市中心变电站数量增多以及人们对居住环境要求的提升,噪声扰民以及居民投诉越来越多。首先研究变电站内变压器噪声的特点,发现变电站噪声能量较大的频率分量主要为500Hz以下的低频噪声,且为100Hz整倍数的频率,这些特征频率信号在一段时间内比较稳定,不会发生突变。针对传统变电站噪声无源控制方法的不足,本文结合自适应有源噪声控制技术,提出了一种改进的变步长LMS自适应滤波算法。通过仿真验证了改进算法的性能,并对实测数据进行处理,结果表明算法可以使变电站降噪达到满意的效果。本文重点是变电站噪声和改进变步长LMS自适应滤波算法研究。
变压器噪声;收敛速度;收敛精度;变步长
1 引言
近年来,随着城市中心变电站数量增多和人们对生活居住环境品质要求的提升,噪声扰民以及居民投诉越来越多。文献资料和实测数据显示变电站噪声主要为变压器产生的低频噪声[1-4],其峰值频率在500Hz以内,由于低频噪声衰减慢、声波长、穿透力强,能轻易穿越障碍物,长距离奔袭和穿墙透壁直入人耳,难治理,对变电站周边居民影响较大。目前变电站采用的传统无源控制技术,主要是通过吸声处理、隔声处理,使用消声器、振动隔离、阻尼减振以达到降低噪声的目的。其不足的地方是对低频噪声控制的效果不明显,且施工量很大。而有源控制(Active Noise Control,简称ANC)[5-7]技术是通过构建与噪声声波幅值频率相等、相位相反的次级声波,与原来噪声在一定区域内叠加、相互抵消以达到降低噪声的目的。其低频降噪效果明显、体积小、成本低。
本文在许多专家学者提出的多种变步长自适应滤波算法基础上[2-6],结合变电站变压器的噪声特点,对其进行改进,使算法性能得到了一定程度的改善。本文提出的改进算法能在降低对噪声的敏感性、达到比较高的收敛精度的同时,大幅降低噪声信号,从而达到降低噪声的要求。本文对其他的噪声控制以及噪声控制装置研制有一定的参考价值。
2 变压器噪声信号分析及降噪方案
2.1 实测变压器噪声特性分析
对已知的算法进行改进,首先需要知道算法所应用对象的特性。为此,对南京江东门110kV变电站变压器四周的噪声进行测量,测量距离为2m。然后对噪声信号进行初步分析,得到如图1所示的噪声时域及其频谱图。
从变电站实测变压器噪声信号的频谱图中发现:变压器噪声中能量较大频率分量主要集中在500Hz以下,为100Hz(电网频率的两倍)整倍数的频率,可以认为变压器的噪声为线谱噪声;而且这些特征频率信号在一段时间内比较稳定,不会因外界干扰而发生突然变化。以上特征和参考文献[1,3,4]中的情况一致。由于噪声频率越高,衰减越快,因此以能量最大的低频分量为重点,构建相关参考信号,针对变电站内变压器的低频噪声研究自适应滤波算法。

图1 变电站实测变压器噪声Fig.1Substation measured transformer noise
2.2 变电站变压器降噪系统及方案
通过对变电站自适应有源噪声控制的研究,设计自适应有源噪声控制系统,单通道有源噪声控制器系统结构如图2所示。系统主要由传声器、外围信号调理以及处理控制三部分组成。传声器部分包括扬声器和测量传感器;外围信号处理部分包括信号放大器、高频滤波、A/D转换、D/A转换和低频功率放大器等。实际应用时,应根据变压器尺寸大小,在变压器四周布放有源噪声控制装置,对变压器周围的噪声进行控制。
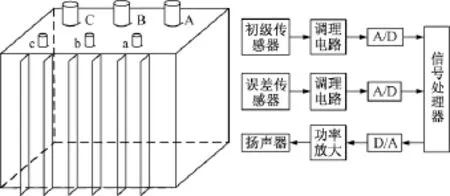
图2 系统总体设计示意图Fig.2Schematic diagram of overall system design
有源噪声控制器系统的工作原理为:前置放大器分别放大初级传感器采集的噪声信号、误差传感器的误差信号,然后微弱信号经过调理电路放大,再经过A/D将模拟信号转换为数字信号。DSP读取转换后的数据进行自适应运算控制,将运算的结果送D/A转换器,D/A转换器输出模拟信号到扬声器,如此循环往复,最终达到降低变电站噪声的目的。
3 改进变步长最小均方误差(LMS)自适应滤波算法及分析
3.1 滤波-XLMS算法原理
设参考信号为x(n),初级信号为p(n),次级声源的输出信号为y(n),次级声源和初级噪声源叠加后的误差信号为e(n)。
在实际应用中,常采用FXLMS算法,它使参考信号通过一个与次级通路Hs(z)相同的附加通路,达到更新LMS算法中权系数的目的,解决因误差信号e(n)产生延时导致的误差信号与参考信号x(n)在时序上无法正确“对齐”的问题。系统控制图如图3所示,H^
s(z)为Hs(z)的近似,W(z)为自适应滤波器,采用有限脉冲响应结构。

图3 FXLMS算法控制系统框图Fig.3Adaptive active control system block diagram
参考信号与初级信号的关系是:
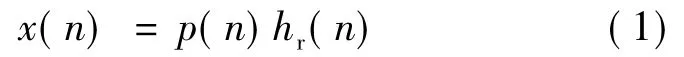
在误差传感器处,接收到的初级声场和次级声场信号分别为:

式中,d(n)为期望信号。应用横向结构FIR滤波器形式,设滤波器长度为L,将第n时刻横向滤波器的权系数和参考输入表示为矢量形式:

次级信号由参考信号计算获得:

假设初级噪声具有局部平稳性,则可以认为自适应滤波权系数在L时段内基本不变。将式(6)代入式(3)次级信号关系式整理得到:
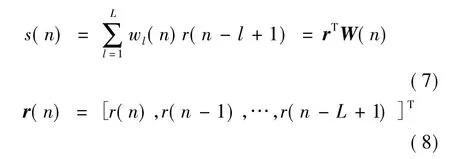
r信号矢量与参考信号矢量的关系是:
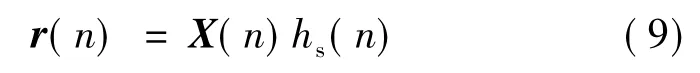
于是,误差传感器接收到的信号可表示为:

自适应算法主要采用最小均方算法,根据最速下降原理控制器参数向量W(n)的修正量为:

第n+1时刻自适应控制器的参数向量W(n)的调整公式为:

式中,μ为收敛系数,也即步长因子。
3.2 改进变步长自适应滤波算法及分析
由于最小均方误差算法使用的是固定步长因子,所以该算法具有先天缺陷。为了提高自适应滤波性能,人们提出了许多变步长自适应滤波算法,如归一化最小均方误差算法、Gitlin R D在文献[8]中提出的变步长算法等。高鹰等人在前人研究的基础上提出了一种新的变步长算法[9],其算法的迭代公式为:
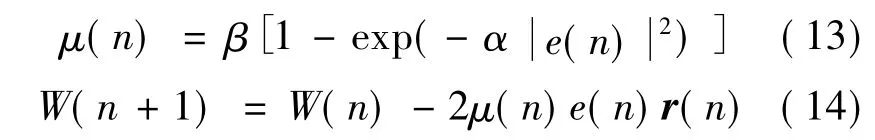
式中,参数α>0控制函数的形状;参数β>0控制函数的取值范围。通过根据跟踪环境和输入信号的分布选取合适的参数α和β,能够使该算法具有较快的收敛速度和收敛精度。
该算法中,用e2(n)调节步长因子,使误差信号中不可避免地会引入一些噪声。如果误差信号中包含的噪声具有很强的自相关性,将会造成步长因子μ大的起伏,从而影响算法的收敛速率和收敛精度。而参考文献[10]提出的算法利用e(n)e(n-1)来调节步长因子,能很好地降低算法对噪声信号的敏感性。
这样变步长自适应滤波算法的迭代公式变为:
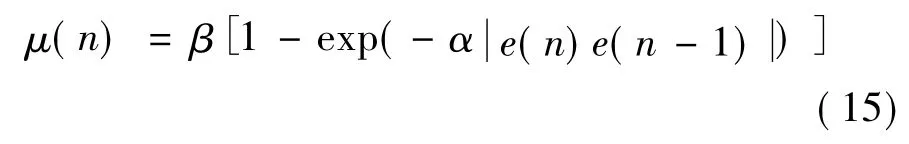

由于μ(n)和e2(n)成指数关系,使得该算法不具有很高的收敛精度,会使得μ(n)随e(n)的变化起伏性太大,e(n)收敛精度降低,具体的不足会在下文的算法仿真比较部分进行说明。本文在前人研究的基础上,兼顾变步长和μ(n)的起伏性提出如下的自适应滤波算法,迭代公式为:
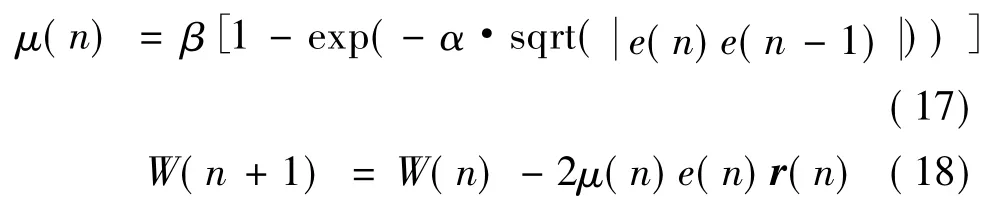
由变步长算法的目的可知,α和β的取值应该遵循的原则是:在e(n)较大时,对应的μ(n)应该较大,以保证算法有较快的收敛速度;当e(n)很小直至达到最小值即算法进入稳态时,对应的μ(n)也应达到最小,以保证算法具有高的收敛精度。根据式(17)可知,μ的最大值为β,则可知当β<1/λmax时,算法一定收敛。在具体实际应用中,可通过仿真实验来确定最优的α、β值。
4 算法仿真及结果分析
4.1 确定α、β参数仿真分析
为了使算法在应用中达到最好的效果,首先对μ(n)和e(n)的关系进行仿真。图4和图5分别是μ(n)和e(n)函数关系曲线图,图4中β固定,α不同;图5中α固定,β不同。

图4 μ(n)和e(n)的函数关系曲线(β相同,α不同)Fig.4Function curves of μ(n)and e(n)(same β,different α)
通过观察图5的曲线发现,固定β,选择较大的α,算法收敛速度较快。但当α值过大时,收敛后误差e(n)对应的μ(n)仍然较大,造成算法收敛精度降低。由图5可知,当固定α时,选择大的β算法的收敛速度较快,但如果β过大会造成不收敛或收敛精度降低。所以,在具体实际应用中,可通过仿真实验来确定最优的α、β值。

图5 μ(n)和e(n)的函数关系曲线(α相同,β不同)Fig.5Function curves of μ(n)and e(n)(same α,different β)
由于变压器噪声中能量较大的基本为周期性的低频噪声,且很平稳,而非平稳随机噪声很小,可以忽略不计。因而,变电站的噪声抑制更侧重算法的收敛性,即能较大程度地对周期性信号分量进行抑制,保证收敛精度。所以,针对变电站噪声抑制的算法中,α、β值不能取得太大。
4.2 改进变步长算法比较仿真
为验证本文算法的有效性,比较算法改进前后的差异,利用Matlab进行仿真分析。首先构造输入信号x(n)=s(n)+v(n)。
其中,v(n)=0.2·randn(1,N),为非平稳随机信号;s(n)=cos(2π·100t)+cos(2π·200t),为平稳的100Hz和200Hz分量噪声信号,然后构建以x (n)为参考信号的变步长自适应控制算法。仿真时,参数α=5、β=0.04。本文改进算法和文献[10]的算法比较如图6所示。

图6 算法比较仿真Fig.6Comparison of algorithms simulation
从图6可以看出,参考文献[10]的变步长算法能很快地响应信号的变化,收敛速率比较快,但收敛精度不是很高,不符合变电站降噪的目标要求。而本文的改进变步长自适应滤波算法的收敛精度比较高,收敛速率也不慢,随着时间的变大,剩余误差信号逐渐趋于0。因此,本文的改进算法更适合变电站的低频平稳的周期信号噪声。
4.3 改进变步长算法对变压器噪声抑制效果分析
前面内容是分析本文改进变步长算法的可行性和优越性,下面将对变电站采集的实测变压器噪声信号进行抑制分析,观察抑制效果。算法中参数α、β选择为:α=50、β=0.4,变压器噪声原始参考输入信号和去噪后的信号如图7所示。
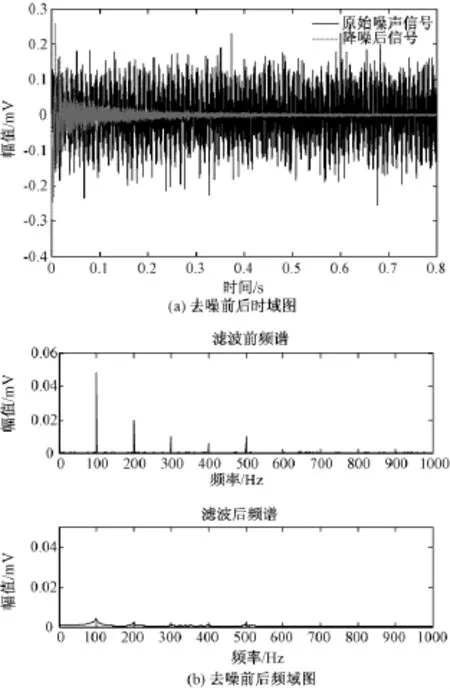
图7 去噪前后的结果分析Fig.7Analysis of results before and after denoising
图7(a)是去噪前后时域比较图,图7(b)是去噪前后频谱分析图。从图7(a)时域图中可以发现:对噪声进行滤波抑制后,在短时间内就可以使噪声剩余量很小,趋近于0。从图7(b)去噪前后的频谱图中可以发现:周期噪声信号基本滤除,诸如汽车、工地、说话等非周期信号还有一定的剩余,由于非周期信号的不可预知性,对其抑制比较难。由于本算法已经能够有效地降低能量较大的低频周期噪声信号,故使降噪达到满意的效果。当然,在变电站变压器噪声抑制的应用中,要注意参考信号与噪声信号的相关性,相关性越大,自适应噪声抵消系统的噪声效果越好。
5 结论
通过对变电站实测变压器噪声分析得出:变电站中低频噪声中能量较大频率分量相对比较确定,主要是500Hz以下的低频分量,且这些特征频率信号在一段时间内比较稳定,不会因外界干扰而发生突然变化。本文提出了一种改进的变步长LMS自适应滤波算法,该算法可以在大幅降低噪声信号的同时降低算法对噪声的敏感性,同时有效改善算法收敛速度和收敛精度。通过对实测信号的应用,得出本算法能够有效地降低能量较大的低频周期噪声信号。本文的研究为今后变电站降噪装置的研制开发提供一定帮助。在变电站噪声抑制的实际应用中,应考虑现场各种复杂情况,合理布置降噪装置,才能使变电站降噪达到满意的效果。
[1]袁聪波,黄家彬(Yuan Congbo,Huang Jiabin).变电站噪声分析及治理(The substation noise analysis and governance)[J].上海电力(Shanghai Electric Power),2002,(4):59-61.
[2]叶建斌,陈雁(Ye Jianbin,Chen Yan).变电站环境噪声现场测试分析与讨论(Analysis and discussion on field measurement of substation ambient noise)[J].广东电力(Guangdong Electric Power),2005,(10):53-56.
[3]吴高强,程胜高,黄磊,等(Wu Gaoqiang,Cheng Shenggao,Huang Lei,et al.).户外220 kV变电站噪声环境影响预测研究(Prediction on noise of 220 kV outdoor substation to environmental infection)[J].噪声与振动控制(Noise and Vibration Control),2007,(3): 135-137.
[4]王和忠,季小龙,朱如勇,等(Wang Hezhong,Ji Xiaolong,Zhu Ruyong,et al.).电力变压器噪声污染分析及对策(Analysis and countermeasures of power transformer noise pollution)[J].能源与环境(Energy and the Environment),2008,(2):88-90.
[5]徐梅花,王福明(Xu Meihua,Wang Fuming).基于MATLAB的自适应噪声抵消器的设计与实现(Design and realization of adaptive noise canceller based on MATLAB)[J].电子测试(Electronic Test),2009,(11): 43-45.
[6]蒋威(Jiang Wei).基于DSP的自适应有源噪声控制实验系统(Experimental system for adaptive active noise control based on DSP)[J].微计算机信息(Microcomputer Information),2011,27(5):76-77.
[7]李燕绪,毕淑娥(Li Yanxu,Bi Shu’e).基于DSP的自适应滤波系统的设计与实现(The design and implement of adaptive filter system based on DSP)[J].微计算机信息(Microcomputer Information),2009,25(8-2):112-113.
[8]Gitlin R D,Weinstein S D.On the design of gradient algorithms for digitally implemented adaptive filters[J].IEEE Transactions on Circuit Theory,1973,20(2): 125-136.
[9]高鹰,谢胜利(Gao Ying,Xie Shengli).一种变步长LMS自适应滤波算法及分析(A variable step size LMS algorithm and analysis)[J].电子学报(Acta Electronica Sinica),2001,29(8):1-4.
[10]沈大伟,贺思,李正宙,等(Shen Dawei,He Si,Li Zhengzhou,et al.).一种改进的变步长变更新速率LMS自适应滤波算法及仿真(An improved variable step size to change the new rate LMS adaptive filtering algorithm and simulation)[J].电子质量(Electronics Quality),2010,(12):11-15.
Algorithm for substation active noise control
ZHAO Hong-fei1,2,MA Hong-zhong1,CHEN Kai3,WANG Chun-ning3,ZHONG Qin1
(1.College of Energy and Electrical Engineering,Hohai University,Nanjing 211100,China; 2.Yangzhou Department of Jiangsu Electric Power Company’s Maintenance Branch,Yangzhou 225000,China; 3.Nanjing Power Supply Company,Nanjing 210008,China)
With the increase of city center substations and enhancement of people’s living environment requirements,noise nuisance and complaints from residents are becoming more severe.To address this issue,first of all,we studied the substation noise characteristics,and found that larger frequency components of the substation noiseenergy are mainly concentrated below 500Hz,and they are also integral multiples of 100Hz.These characteristic signals are relatively stable over time,and will not be mutated.In the light of the deficiencies of traditional substation noise passive control method,this article presents an improved variable step size LMS adaptive filtering algorithm combined with the adaptive active noise control technology.By simulating,we verify the performance of the improved algorithm and process the measured data by using the improved algorithm.The results show that the noise reduction algorithm can achieve satisfactory results.This article focuses on the substation noise signature and improvs the variable step size LMS adaptive filtering algorithm.
transformer noise;convergence rate;convergence precision;improved variable step size
TM401
A
1003-3076(2014)10-0070-06
2012-10-07
国家电网公司总部2011年重点科技项目(2011-0810-2251)
赵宏飞(1988-),男,江苏籍,助理工程师,硕士,研究方向为电力设备状态检测与故障诊断;马宏忠(1962-),男,江苏籍,教授/博导,研究方向为电力设备状态监测与故障诊断,电能质量监控。

