环Z2+uZ2+u2 Z2上的斜循环码
李 锦, 朱士信
(合肥工业大学 数学学院,安徽 合肥 230009)
多项式环及其理想一般被用来构造和理解循环码[1-3],在文献[4-5]中第1次提出了利用非交换的斜多项式环F[X,θ]来构造一种更广义的循环码。这些码与循环码和准循环码有相同的结构,分别称为斜循环码和斜准循环码。文献[6]研究了Galois环上的斜循环码。本文将研究环R=Z2+uZ2+u2Z2={0,1,u,u2,1+u,1+u2,u+u2,1+u+u2}的斜循环码,其中u3=1。对任意2个元素a=a0+ua1+u2a2,b=b0+ub1+u2b2∈R的加法和乘法规则如下:
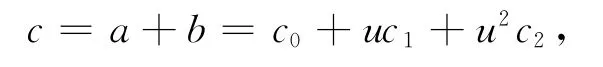
其中,c0=a0+b0(mod 2);c1=a1+b1(mod 2);c2=a2+b2(mod 2)。
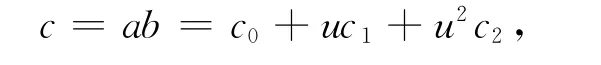
其中,c0=a0b0+a1b2+a2b1(mod 2);c1=a0b1+a1b0+a2b2(mod 2);c2=a0b2+a2b0+a1b1(modp)。
定义环R上的自同构θ如下:
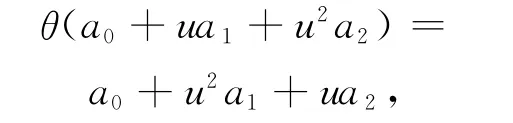
其中,a=a0+ua1+u2a2∈R,ai∈Z2,i=0,1,2。
易知任意a∈R,θ2(a)=a,即θ的阶为2。
1 环R上斜多项式环和斜循环码
1.1 环R上斜多项式环
本文对集合R[X,θ]={a0+a1X+…+anXn|∀ai∈R,i=0,1,…,n}定义加法和乘法来构造一个非交换环,集合R[X,θ]中多项式的系数都在变量X的左边;定义加法为普通多项式的加法,乘法满足如下规则:
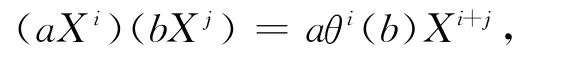
通过结合律和分配律可以得到环R[X,θ]的所有元素。环R[X,θ]是一个非交换环,不满足左右欧几里得,但是可以定义某些元素的左或右整除[7]。
下面讨论R[X,θ]的左或右主理想。
1.2 斜循环码
定义1Rn的子集C是长为n的斜循环码,如果C满足如下2个条件:
(1)C是R上线性码。
(2)(c0,c1,…,cn-1)∈C⇒(θ(cn-1),θ(c0),…,θ(cn-2))∈C。
引理1 如果n是偶数,则(Xn-1)是R[X,θ]的双边理想。
证明 如果Xn-1是一个中心元素,则(Xn-1)是R[X,θ]的双边理想。
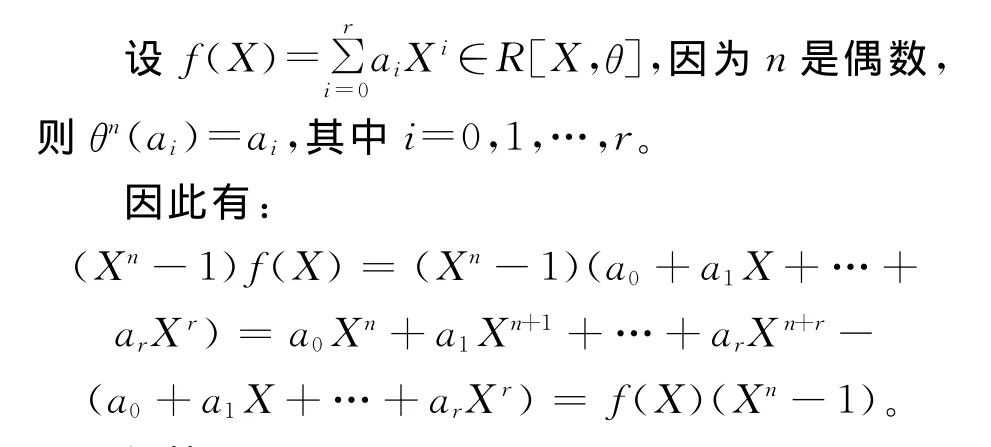
证毕。
下面讨论n是偶数的情况。
对于非交换环Rn=R[X,θ]/(Xn-1)将其等同地看成P∈R[X,θ]在标准映射下的像:
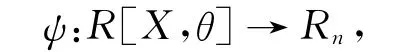
即P在R[X,θ]中右整除Xn-1的余项Pr,记ψ(X)仍为X,这种表示给出了Rn中元素的标准形式,一般将长为n的码字看做是Rn中元素的系数元组。
定理1C是R上长为n的斜循环码当且仅当C是Rn=R[X,θ]/(Xn-1)的左理想。
证明 假设C是R上长为n的斜循环码,则C是线性码且满足:
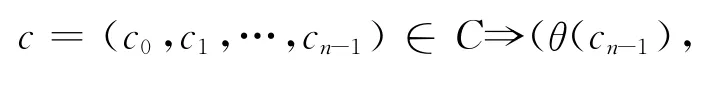
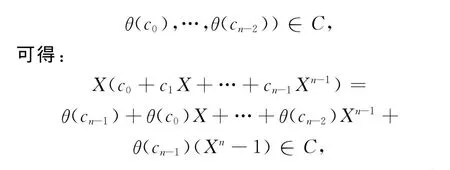
则由线性性可知对任意P(X)∈Rn,P(X)c∈C,即C是Rn=R[X,θ]/(Xn-1)的左理想。
反之,设D是Rn=R[X,θ]/(Xn-1)的左理想,则D是R上长为n的线性码。设d=(d0,d1,…,dn-1)∈D,则Xd(X)=X(d0+d1X+…+dn-1Xn-1)∈D,可得:
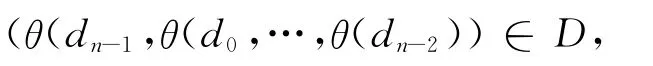
即D是斜循环码。
推论1 首一多项式g(X)是Xn-1的右因子,则C=(g(X))是R上长为n的斜循环码。
设C是Rn=R[X,θ]/(Xn-1)的非零左理想,记A为C中次数最小的非零斜多项式集合,显然A是非空的。下面考虑2种情况:A中存在首一斜多项式;C中没有首一多项式。
定理2 设C和A如上所述,那么:
(1)如果A中存在首一多项式,则C=(g(X)),其中g(X)是A中唯一首一的多项式,g(X)是Xn-1的右因子。
(2)如果C中没有首一多项式,则C=(g(X)),其中其中gi∈{1+u,1+u2,u+u2},0≤i≤r。
证明 (1)假设f(X),g(X)∈A都是首一的,设 deg(f(X))=deg(g(X))=r,由 于deg(f(X))-deg(g(X))<r,可知假设矛盾,所以A中首一的多项式是唯一的。
对任意c(X)∈C,设

其中,deg(r(X))<deg(g(X))。
而r(X)=c(X)-q(X)g(X)∈C当且仅当r(X)=0,所以c(X)=q(X)g(X),即C=(g(X))。
设Xn-1=p(X)g(X)+s(X),其中deg(s(X))<deg(g(X))。类似可知s(X)=0,则Xn-1=p(X)g(X),即g(X)是Xn-1的右因子。
(2)假设C中不存在首一多项式,由环R的加法乘法规则可知任意多项式C有如下2种形式:
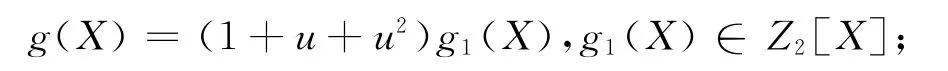
或者
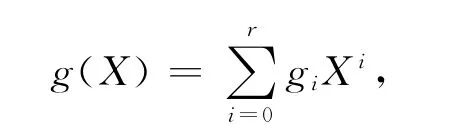
其中,gi∈{1+u,1+u2,u+u2},0≤i≤r。
若∀g(X)= (1+u+u2)g1(X)∈C,g1(X)∈Z2[X]。设h(X)是C中不能被g(X)右整除次数最低的斜多项式,deg(h(X))≥deg(g(X))。
设c(X)=h(X)-Xdeg(h(X))-deg(g(X))g(X),由R乘法规则可知:
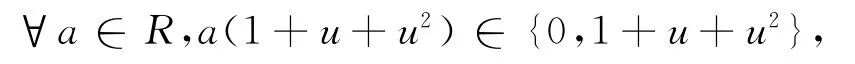
则由deg(h(X))>deg(c(X))可知假设矛盾,所以C中没有不能被g(X)右整除的斜多项式,即C=(g(X))。
设h(X)是C中不能被g(X)右整除次数最低的斜多项式,deg(h(X))≥deg(g(X))。易知∀a∈R,b∈I,ab∈{0}∪I,不妨设h(X)和g(X)的首项系数相同,设c(X)=h(X)-Xdeg(h(X))-deg(g(X))g(X),则 由 deg(h(X))>deg(c(X))可知假设矛盾,所以C中没有不能被g(X)右整除的斜多项式,即C=(g(X))。
定义2R上线性码C如果满足(a0,a1,…,an-1)∈C⇒(an-1,an-2,…,a0)∈C,则称作可逆码[8]。记的可逆多项式,若g(X)=gr(X),则称g(X)是自互反的。记
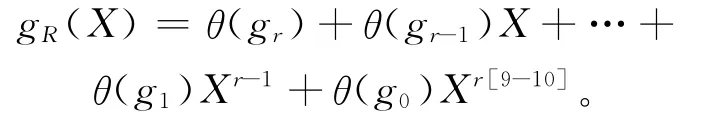
定理3C=(g(X))是R上长为n的斜循环码,若g(X)的首项系数和常数项都为1,则C1=(gR(X))和C2=(gr(X))也是R上长为n的斜循环码。
证明 如果deg(g(X))是奇数,则存在p(X)∈R[X,θ]使得Xn-1=p(X)g(X)。设
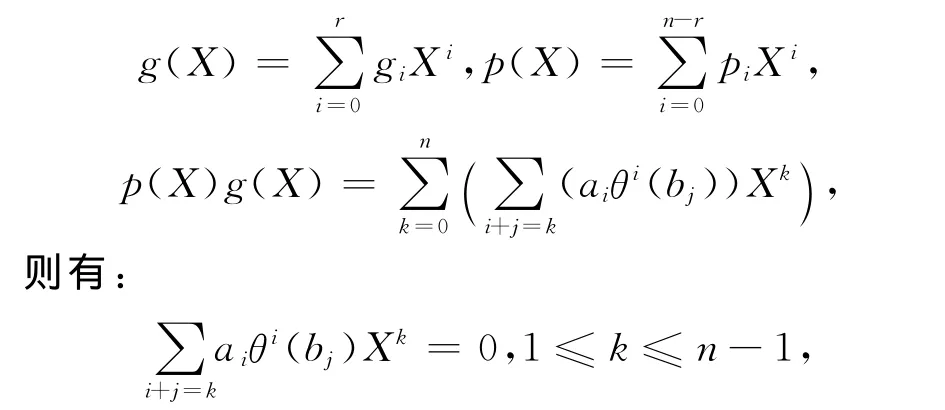
易知Xn-1=pr(X)gR(X)=pR(X)gr(X),即gR(X)和gr(X)是Xn-1的右因子。如果deg(g(X))是偶数,计算可得:
Xn-1=pr(X)gr(X)=pR(X)gR(X),即gR(X)和gr(X)是Xn-1的右因子。
综上所述,由推论1可得结论。
定理4 设C=(g(X))是R上长为n的斜循环码,g(X)的首项系数和常数项都为1。如果deg(g(X))是偶数,C是可逆码当且仅当g(X)=gR(X);如果deg(g(x))是奇数,C是可逆码当且仅当g(X)是自互反的。
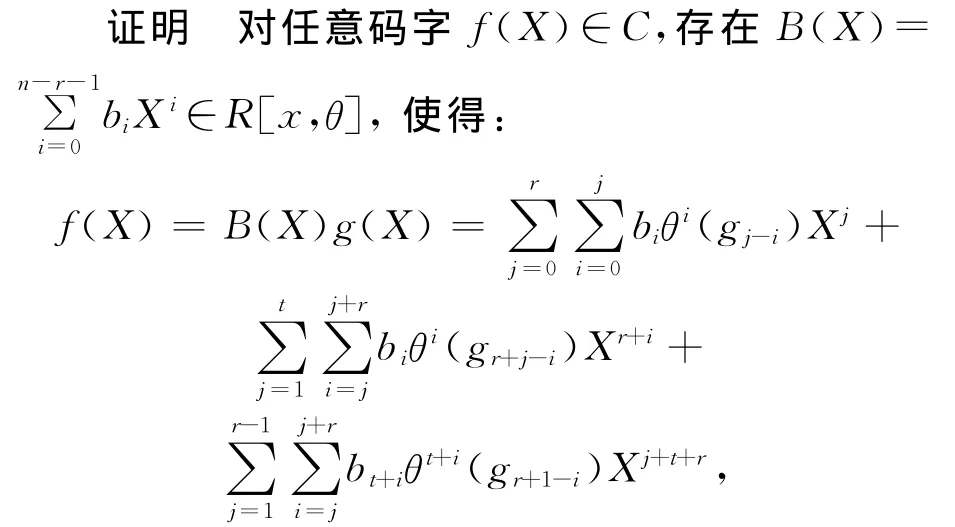
其中,bi∈R。记fr(X)是f(X)的可逆码,如果deg(g(X))是奇数,由于|〈θ〉|=2,可得fr(X)=Br(X)gr(X)。对于Br(X)共有23(n-r)种可能,可以得到由gr(X)生成的斜循环码,而该码与原码C相同当且仅当g(X)=gr(X)。类似地,如果deg(g(x))是偶数,可得fr(X)=Br(X)gR(X),则C是可逆码当且仅当g(X)=gR(X)。
2 斜循环码的对偶码
设x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈Rn,记Rn中的Euclidean内积如下:

码C关于Euclidean内积对偶码C⊥如下:
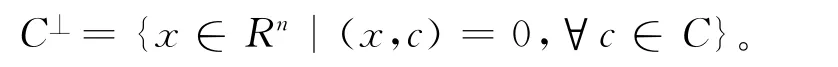
如果C=C⊥,称C是Euclidean自对偶的,码C关于Hermitian内积对偶码C*如下:
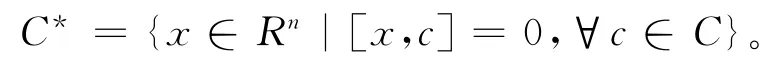
如果C=C*,称C是Hermitian自对偶的。
定理5 斜循环码关于Euclidean和Hermitian内积的对偶码仍是斜循环码。
证明 设C是R上长为n的斜循环码,设c=(c0,c1,…,cn-1)∈C,b=(b0,b1,…,bn-1)∈C⊥,d=(d0,d1,…,dn-1)∈C*。因为C是斜循环码,则有:
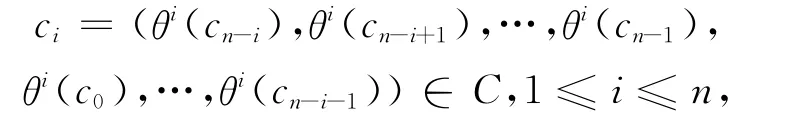
则〈ci,b〉=0,1≤i≤n。如果i=n—1,则i为奇数且θi(a)=θn-1(a)=θ(a),∀a∈R。可得:

则有:

由此可知(θ(bn-1),θ(b0),…,θ(bn-2))∈C⊥,所以C⊥是斜循环码。
类似可证C*也是斜循环码。
[1]MacWilliams F J,Sloan N J A.The theory of error-correcting codes [M ]. Amsterdam: North Hoalland,1977:189-196.
[2]Wan Zhexian.Quaternary codes[M].Singapore:World Scientific,1997:93-104.
[3]黄成宝,朱士信.环F2+uF2+u2F2上线性码及其Gray象的生成矩阵[J].合肥工业大学学报:自然科学版,2009,32(9):1436-1438.
[4]Boucher D,Geiselmann W,Ulmer F.Skew cyclic code[J].Applied Algebra in Engineering Communication and Computing,2007,18(4):379-389,1441.
[5]Boucher D,Ulmer F.Coding with skew polynomial rings[J ]. Journal of Symbolic Computation, 2009,44:1644-1656.
[6]Boucher D,SoléP,Ulmer F.Skew constacyclic codes over Galois rings[J].Advances in Mathematics of Communications,2008,2(3):273-292.
[7]Ore O.Theory of non-commutative polynomials [J].The Annals of Mathematics,1933,34:480-508.
[8]Massey J L.Reversible codes[J].Information and Control,1964,7:369-380.
[9]Boucher D,Ulmer F.Codes as modules over skew polynomial rings[J].Lecture Notes in Computer Science,2009,5921:38-55.
[10]McDonald B R.Finite rings with identity[M].New York:Marcel Dekker,1974:22-28.

