基于蟑螂算法的产品拆卸序列规划
施英莹, 刘志峰, 张洪潮,2, 胡 迪
(1.合肥工业大学 机械与汽车工程学院,安徽 合肥 230009;2.德克萨斯理工大学 工业工程系,拉伯克 79409)
对废弃产品进行回收和重利用能大大减轻环境污染,拆卸是产品回收的重要环节,如何拆卸已经成为全球性的重要研究课题[1]。拆卸序列规划就是通过对产品装配信息进行分析、提取,生成几何可行的拆卸序列,同时根据一定的评价标准,寻找最优的拆卸序列。近年来,国内外很多学者对其进行了深入研究。早期的研究主要倾向于图论研究,包括 AND/OR 图法[2]、Petri网法[3]、割集图法[4]等。这些方法在一定程度上解决了拆卸中的序列生成问题,但是当零件数目较大时,会出现组合爆炸现象。近来,随着进化算法的发展,基于人工智能算法求解最优拆卸序列的研究受到了重视。文献[5]基于组件数量、拆卸工具以及拆卸方向的考虑建立了拆卸优化模型,然后运用蚁群算法得到了有效的产品拆卸序列。文献[6]构建了产品拆卸可行性信息图,并引入了遗传算法进行最优拆卸序列的搜寻。文献[7]将赋权混合图模型映射到粒子群模型,应用粒子群算法实现了复杂产品的拆卸序列优划。然而,这些算法都易陷入局部最优,在进化后期收敛速度较慢,优化精度较差。
蟑螂算法(Cockroach Swarm Optimization,简称CSO)是通过模拟蟑螂(Cockroach,简称C)的觅食行为和简化社会模型而提出的一种新型智能算法,CSO算法公式简单,充分利用了C社会的平等特性和群体智慧,通过群体协作达到寻优目的,再分配和大变异策略使算法具有较强的全局搜索及跳出局部最优的能力[8-9]。本文将CSO算法用于产品拆卸序列规划,通过建立产品拆卸混合图来产生可行的初始拆卸序列,建立拆卸成本最小的目标函数,并结合CSO算法进行拆卸序列规划,以得到最优或近似最优的拆卸序列。
1 基于混合图的拆卸模型的建立
1.1 拆卸模型描述
产品一般由零件或部件组成,在建立混合图时,需要把部件当作零件来看,定义混合图的顶点为产品的零件或部件。
首先对产品拆卸建模作如下假设[10-11]:
(1)产品零件或部件分为功能件和连接件,连接件指用来连接和固定功能件的零件或部件。混合图中的零件或部件均指功能件。
(2)产品拆卸需求信息(包括拆卸零件信息,主要考虑零件或部件间的连接关系;拆卸工艺信息,主要考虑拆卸过程所需的工具;拆卸约束信息,主要考虑零件或部件的拆卸方向)都作为已知条件,转换成0-1矩阵。
在获取产品拆卸信息的基础上,建立混合图来描述产品零件或部件间的关系。混合图由表示零件或部件的顶点、零件或部件间连接关系的实线无向边以及零件或部件间优先关系的虚线有向边构成,拆卸就是把这些零件或部件从产品中分离出来的过程。图1所示为其混合图。
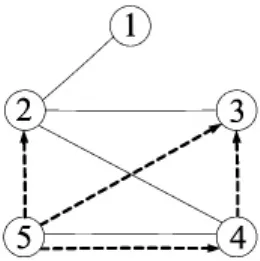
图1 拆卸混合图
表示为:
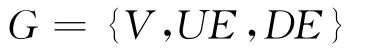
其中,G表示混合图;V为顶点,表示零件或部件;UE为实线无向边,表示零件或部件间的接触约束关系(如图1中顶点1到2为无向边,表示零件1和2间有连接关系);DE为虚线有向边,表示零件或部件间的优先关系(如图1中顶点5到2为有向边,表示零件5应在2之前拆卸)。
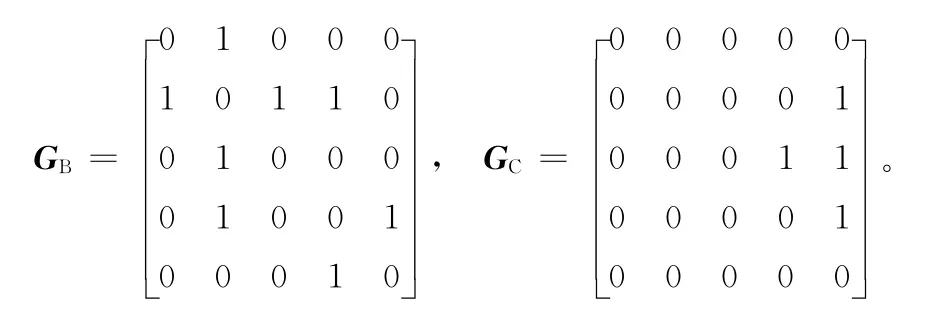
混合图中的无向边和有向边可以表示成连接矩阵和优先矩阵,G={V,UE,DE}可以分解为GB={V,UE}和GC={V,DE}。假设混合图含有N个顶点,则G可以分解为2个N维矩阵,即
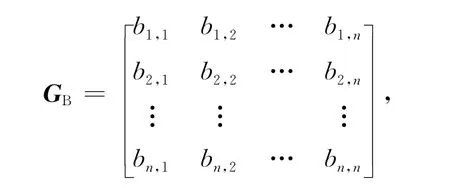
其中,当零件i与零件j有接触连接时,bi,j=1;当零件i与零件j没有连接关系时,bi,j=0;当i=j时,bi,j=0。
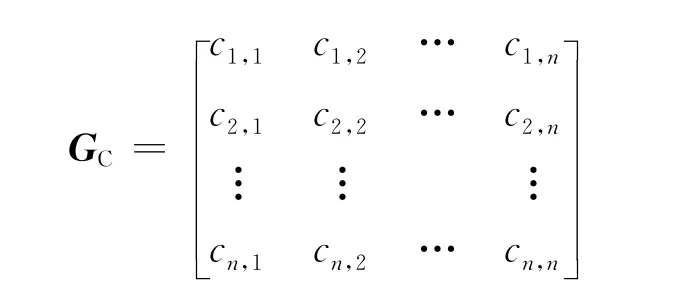
其中,当零件j须在零件i前拆卸时,ci,j=1;当零件i与零件j间无优先关系时,ci,j=0;当i=j时,ci,j=0。
图1所示的拆卸混合图表示为2个矩阵,即
1.2 可拆卸零件推导及初始拆卸序列生成
可拆卸零件是指可以从产品中分离出来的零件,根据混合图模型的2个矩阵可以判断零件是否可拆卸。当零件i同时满足以下2个条件:① 零件i只有一个接触连接;② 零件i没有受到其他零件的优先约束时,零件i可拆卸;否则,零件i不可拆卸。当零件i被拆卸后,在混合图中,零件i与其他零件间的约束关系都被解除,即顶点i变成了一个孤立点。拆卸结束时,混合图将由一些孤立点组成。
初始拆卸序列的质量对搜索效率有很大的影响。为了在人为给定和随机生成之间取得平衡,保证搜索效率,根据零件的可拆卸性推导,按照串行方式逐步生成初始拆卸序列。首先定义列表allowed存放可拆卸零件,定义列表sequence存放当前获得的拆卸序列。例如,拆卸对象为图1产品,根据条件① 和② 可判断allowed={1,5},随机选取零件5放入sequence中,使sequence={5},更新混合图使顶点5变成孤立点;然后用同样的方法判断allowed={1,4},随机选取零件1放入sequence中,使sequence={5,1},更新混合图将顶点1变成孤立点;以此类推,最后1、2、3、4、5都变成孤立点,生成一条可行拆卸序列sequence={5,1,4,3,2}。初始拆卸序列生成的具体流程如图2所示。
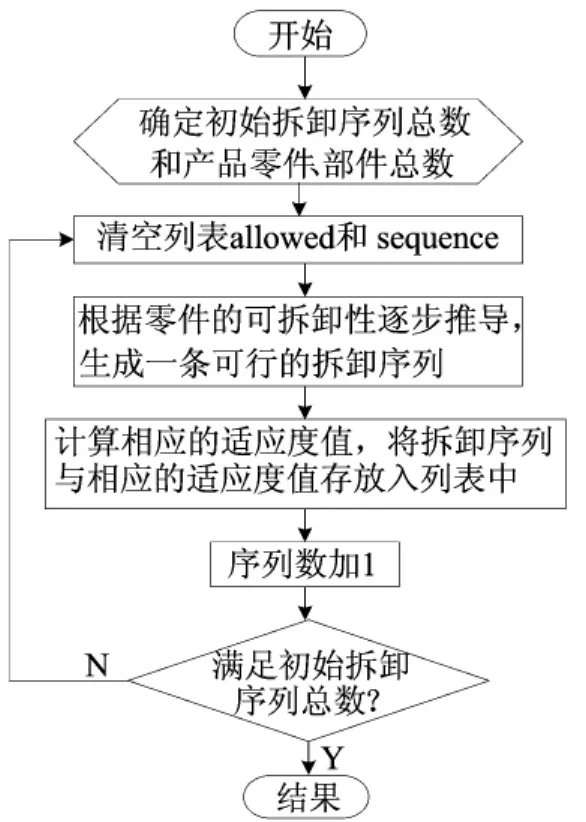
图2 初始拆卸序列的生成
1.3 拆卸序列优化
拆卸序列规划的目的是得到拆卸成本较低的拆卸序列。对完全拆卸而言,拆卸过程中拆卸方向的改变次数和拆卸工具的更换次数是影响拆卸成本的2个最大因素。优化算法的目的就是尽可能减少拆卸方向和拆卸工具的变化,以降低成本,提高拆卸效率[12]。根据分析,对这2个评价指标进行加权,确定拆卸序列优化的目标函数为:
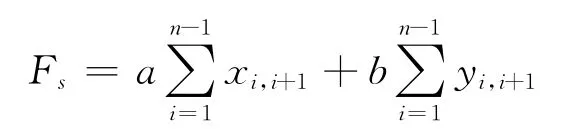
其中,s为可行的拆卸序列;a为拆卸方向改变权值;b为拆卸工具更换权值。

2 拆卸序列优化模型的求解
2.1 算法原理及模型映射
CSO算法是从自然界中C觅食过程得到启发,通过改进而得到的一种算法,通过C群体的集体协作达到寻优目的。拆卸序列规划属于离散组合优化问题,用CSO求解该问题时,需要通过下面的关系映射,将拆卸序列规划的图模型与CSO模型对应起来。
在产品混合图模型G的基础上,每个C的位置坐标Ci={c1,c2,…cn}代表一条拆卸序列,n为零件个数,ci代表零件i。例如,C1{5,3,2,4,1,6}就代表拆卸序列5→3→2→4→1→6。C的位置坐标对应的适应度值确定了对应拆卸序列的优劣程度,对拆卸成本函数,适应度值越小,对应的拆卸序列越优秀。每个C根据自身、自身的局部最优位置和整个群体的全局最优位置不断爬行,寻找满足条件的最优解[13-15]。
(1)交换路径。C爬行一步用Step(i,j)表示,代表拆卸序列中零件i和零件j交换。C爬行一段距离表示拆卸序列经过若干次交换,表示Road=Step1+Step2+…+Stepm。
例如,当前拆卸序列为(2,4,3,6,5,1),目标拆卸序列为(3,6,1,4,2,5),交换路径为:Road=Step(1,3)+Step(2,4)+Step(3,6)+Step(5,6),如图3所示。
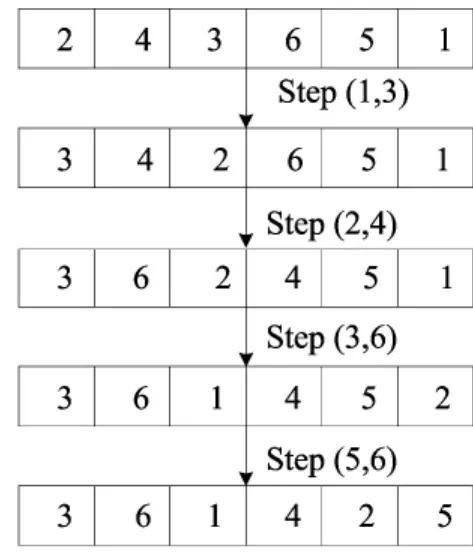
图3 交换路径
(2)再分配策略。设m为C群体规模,即初始拆卸序列总数;Fg为全局最优解,即所有拆卸序列中适应度值最小的拆卸序列;Fpi(i=1,2,…,m)为局部最优解,即每个初始拆卸序列对应的、除Fg外适应度值最小的拆卸序列。随着算法的不断迭代,可能会出现Fg=Fp1=Fp2=…=Fpm,使算法陷入局部最优,此时要采取再分配策略,对Fpi进行重新分配:
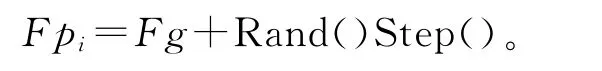
(3)回巢策略。每次向Fg或Fpi爬行前,C群体重新回到初始位置,即所有的初始拆卸序列不变化。回巢策略使算法具有全局搜索能力,从而避免早熟。
(4)大变异策略。把所有C向Fg和Fpi(i=1,2,…,m)爬行完成作为一次总迭代,即把所有初始拆卸序列向Fg和Fpi(i=1,2,…,m)交换完成的过程作为一次总迭代,用FgRemb记录当前全局最优拆卸序列。如果T次迭代FgRemb不更新,则执行大变异策略:
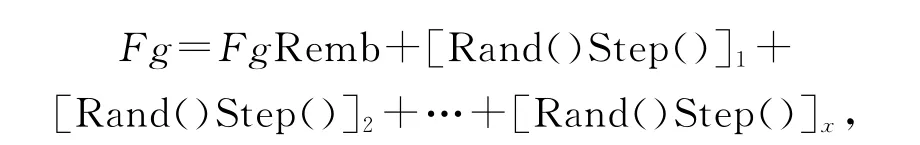
其中,x∈[1,n/5],n为零件个数。
大变异策略使CSO算法跳出局部最优,使Fg在一个新的位置引领所有C在空间内搜索最优解。
2.2 基于CSO算法的拆卸序列规划
最优化拆卸序列求取流程如图4所示。
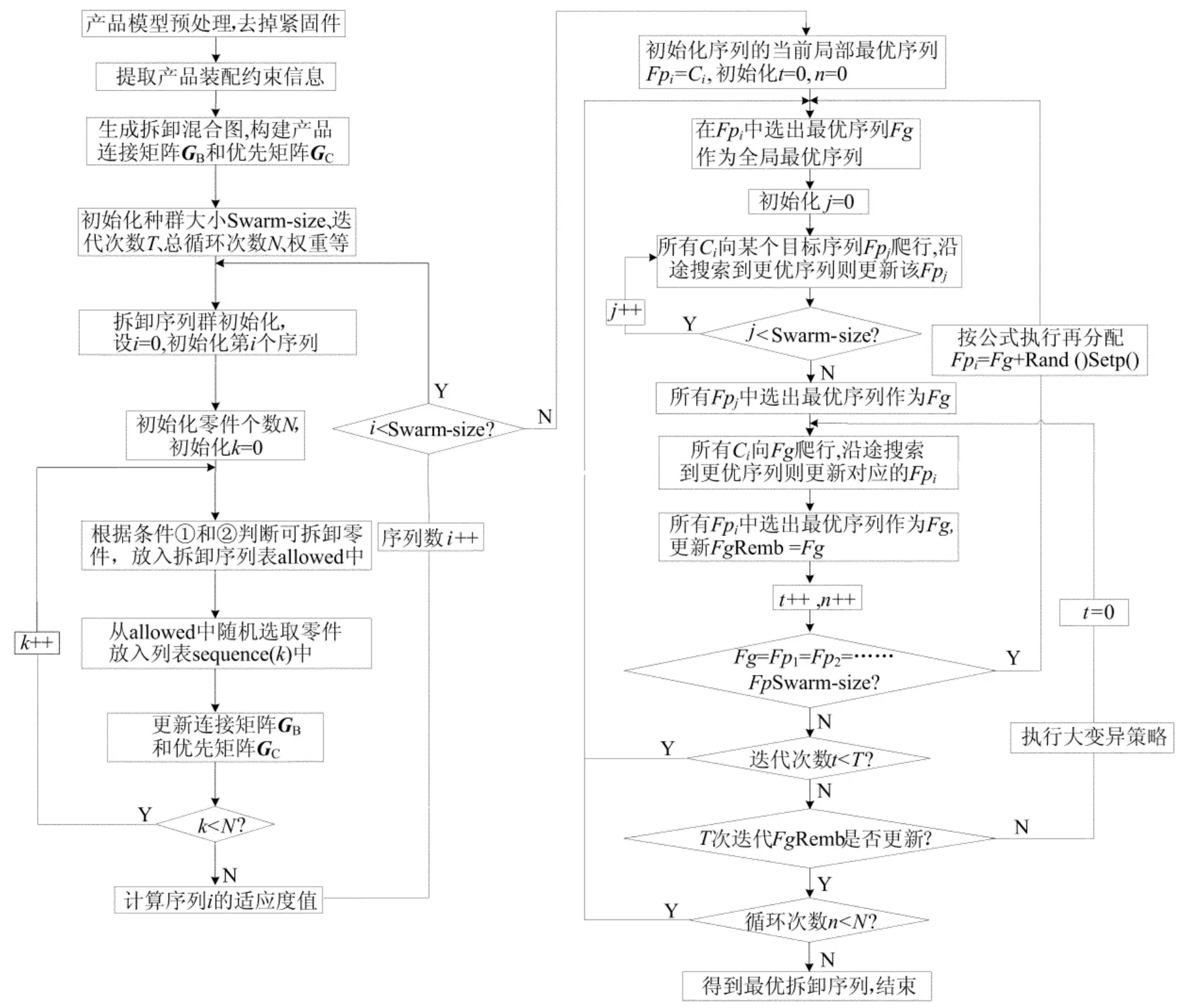
图4 拆卸序列优化流程图
利用CSO优化算法进行产品序列规划的实质是将基于图搜索和智能算法相结合。
(1)建立产品混合图模型,根据连接矩阵和优先矩阵得到可行的初始拆卸序列群,初始化个体的局部最优拆卸序列Fpi(初始化时,可设Ci=Fpi对算法无影响)。
(2)对一个局部最优目标拆卸序列Fpi,所有初始拆卸序列同时向其爬行,交换过程中,若沿途搜索到适应度值小于Fpi序列的更优解,则更新该Fpi;初始拆卸序列对所有Fpi爬行完成后,在Fpi中选出适应度值最小的作为当前全局最优目标拆卸序列Fg。
(3)所有初始拆卸序列向Fg爬行,沿途搜索到适应度值更小的拆卸序列则更新对应Fpi;所有初始拆卸序列向Fg爬行完成后,在Fpi中选出适应度值最小的序列更新Fg,记录FgRemb=Fg;步骤(2)、(3)表示一次完整的交换过程。
(4)判断拆卸序列Fg=Fp1=Fp2=…=Fpm是否成立,若成立则执行再分配策略,重新得到局部最优目标拆卸序列Fpi,转入步骤(2);若不成立则直接转入步骤(2),直至T次迭代结束。
(5)判断T次迭代过程中FgRemb是否更新,若更新则直接转入步骤(2)进行下一轮循环;若不更新则执行大变异策略,转入步骤(3)。
(6)判断循环次数是否达到N,若达到则退出算法,输出最优拆卸序列;若没达到则转入步骤(2)继续循环。
3 实例研究
基于求解算法,使用VC++6.0编写了相应的CSO优化算法程序。本文以某款柜式洗碗机为例,模型的爆炸图如图5所示。该洗碗机模型中共包含14个功能件,各功能件的信息见表1所列。

图5 洗碗机模型爆炸图
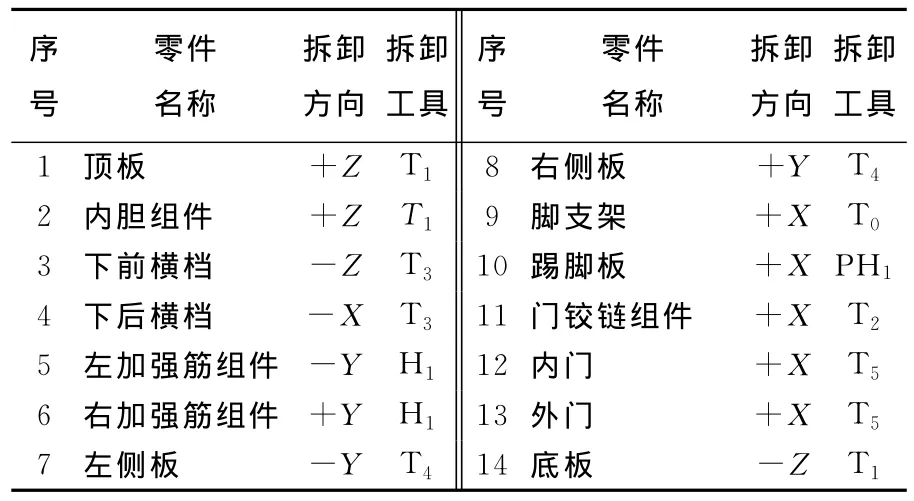
表1 洗碗机零部件信息表
在洗碗机的拆卸过程中,由于洗碗机体积较大,拆卸方向的改变对整个拆卸影响也较大。其拆卸混合图如图6所示。
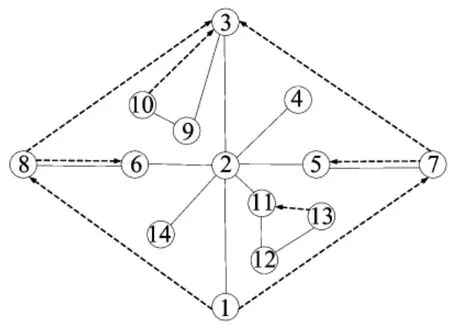
图6 洗碗机模型混合图
同时,拆卸过程中对不同的拆卸对象,有不同的拆卸工具,拆卸工具更换的影响相对较小。因此,目标函数F中权值分别为:a=0.6,b=0.4,算法中迭代次数T=5,经过反复多次试验,CSO算法中参数变化对结果的影响见表2所列。从表2可以看出,CSO算法的最优解受初始种群的影响较大,而在初始种群相同的情况下,循环次数越多,获得最优解的可能也越大。在种群规模均为60,循环次数均为80的情况下,CSO算法和PSO算法的结果对比见表3所列,由表3可以看出,CSO算法得到的结果较优于PSO算法。
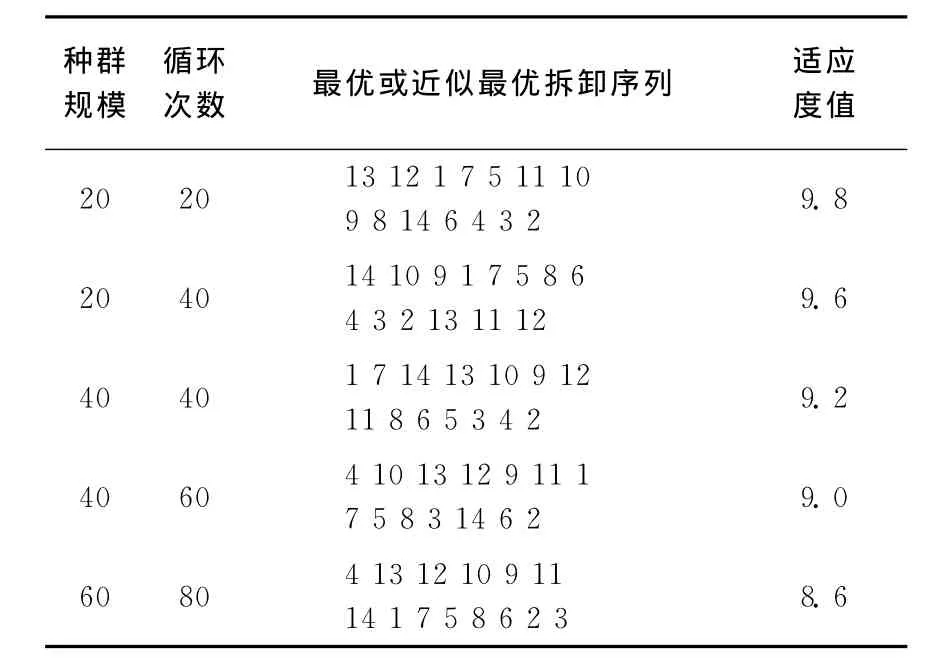
表2 各次主要试验结果
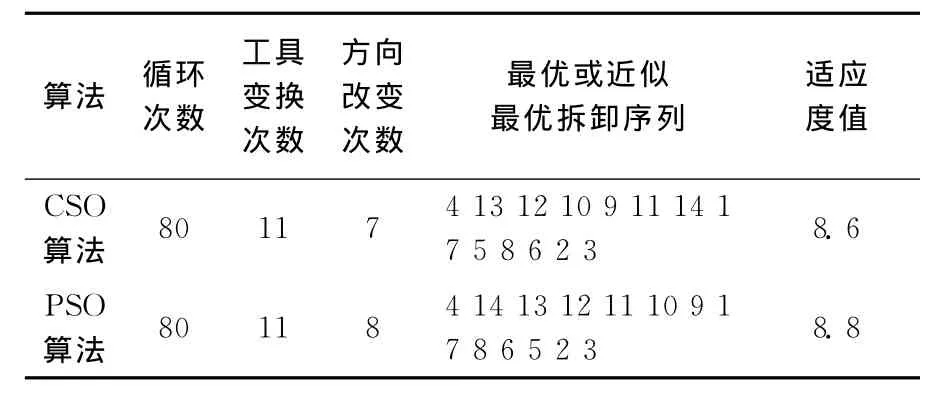
表3 CSO算法和PSO算法结果对比
4 结束语
产品拆卸规划包括拆卸序列产生和拆卸序列优化2部分,在现有拆卸序列规划研究的基础上,用混合图来描述产品的拆卸模型,通过混合图推导生成可行拆卸序列,提出拆卸序列优化目标函数,结合CSO算法对拆卸序列进行优化得到最优或近似最优解。通过实例分析,表明了本文提出的拆卸序列规划模型能够处理拆卸序列规划问题。但是CSO优化算法仍然存在一些不足,作为一个新的优化算法,CSO仍需改进,使其更适用于拆卸序列规划。
[1]Kim H J,Leed H,Xirouchakis P,et al.Disassembly scheduling with multiple product types[J].Annals of the CIRP,2003,52(1):403-406.
[2]Zussman E,Zhou M C.A methodology for modeling and adaptive planning of disassembly process[J].IEEE Transactions on Robotics and Automation,1990, 15(1):190-194.
[3]Kuo T C.Disassembly sequence and cost analysis for electromechanical products[J].Robotics and Computer Integrated Manufacturing,2000,16(1):43-54.
[4]Guo Weixiang,Liu Zhifeng.Disassembly sequence planning based on modularization [J].Journal of Computer-Aided Design & Computer Graphics, 2005,17(3):498-504.
[5]Shan Hongbo,Li Shuxia,Huang Jing,et al.Colony optimization algorithm-based disassembly sequence planning[C]//ICMA International Conference on Mechatronics and Automation,Harbin,China,2007:867-872.
[6]Wang Hui,Xiang Dong,Duan Guanghong.A genetic algo-rithm for product disassembly sequence planning[C]//IEEE International Conference on Engineering of Intelligent Systems,Islamabad,Pakistan,2006:1-5.
[7]张秀芬,张树有.基于粒子群算法的产品拆卸序列规划方法[J].计算机集成制造系统,2009,15(3):508-514.
[8]Jeanson R,Rivault C,Deneubourg J,et al.Self-organized aggregation in cockroaches[J].Animal Behavior,2005,69:169-180.
[9]Easom E E.A survey of global optimization techniques[D].Louisville K Y:University of Lousisvile,1990.
[10]王 辉,向 东,段广洪.基于蚁群算法的产品拆卸序列规划研 究 [J].计 算 机 集 成 制 造 系 统,2006,12(9):1431-1437.
[11]刘志峰,张少亭,宋守许,等.报废汽车拆卸回收的经济性分析[J].合肥工业大学学报:自然科学版,2009,32(3):347-350.
[12]Lambert A J D.Optimum disassembly sequence with sequence-dependent disassembly costs[C]//Proceedings of the IEEE International Symposium on Assembly and Task Planning,Portugal,2003:151-156.
[13]程 乐.引入大变异策略的蟑螂算法研究[J].微电子学与计算机,2009,26(5):13-16.
[14]Chen Zhaohui,Tang Haiyan.Cockroach swarm optimization[C]//Proceedings of 2010 2nd International Conference on Computer Engineering and Technology,Portugal,2010:652-655.
[15]Havens T C,Spain C J,Salmon N G,et al.Roach infestation optimization[J].Swarm Intelligence Symposium,Portugal,2008:1-7.

