Cu－Al－Ni－Mn－Ti合金热弹性马氏体相变弛豫时间的研究

王建伟， 宫晨利， 叶冠群

（合肥工业大学 材料科学与工程学院，安徽 合肥 230009）

铜基形状记忆合金作为一种重要的记忆功能材料［1］，由于其具有良好的冶金性能、加工工艺性能、相变高阻尼和超弹性以及高导热性、导电性和耐蚀性［2－3］，在许多工业领域中有着重要的应用，特别是其可调相变温度范围宽，经常用来制造低温、中温或高温驱动控制元件。

驱动控制元件的动作机制是基于温度或应力诱导下的马氏体相变，这种热弹性或应力弹性马氏体相变的机制将影响形状记忆功能，从而影响到驱动控制元件在工作过程中的驱动效果，其核心问题是相变弛豫时间。对于热弹性马氏体相变，弛豫时间的物理实质为形核时间［4－5］。实验研究相变弛豫时间随外界变量的关系，并从理论上加以定量分析，具有重要的实际和理论意义［6］。

本文以铜基形状记忆合金作为实验对象，利用多功能低频力学弛豫谱仪对热弹性马氏体相变弛豫进行了研究。力学弛豫技术的特点是测量精度高，可进行多变量测量，对材料内部组织结构变化极为敏感，在凝聚态物理学和材料学中有着广泛的应用。本文采用不同的升温速率测量合金的相变弛豫时间，以探讨在不同升温速率下弛豫时间的变化规律，为合金的应用奠定实验及理论基础。

1 实验材料及方法

Cu－12Al－5Ni－1.6Mn－1Ti属于实用型形状记忆合金，将其熔炼后切割成1mm×4mm×70mm内耗样品。样品在氩气或氮气炉中850℃加热60min后水淬，淬火时发生DO3→M18R1马氏体相变。M18R1属于长周期单斜结构，接近于正交结构，亚结构为高密度堆垛层错［7］，后者对相变内耗的产生起重要作用。

实验在多功能低频力学弛豫谱仪上进行，其核心部分采用葛氏摆，能实现内耗测量的自动化。内耗和相对动力学模量（RDM）（即贮存弹性模量M1）的测量原理是由数字信号发生器产生正弦电压给激发线圈，产生交变磁场作用在竖扭摆上的永久磁铁，在样品上产生扭矩，样品扭转角位移通过光电接收器测量，经计算机处理计算出内耗tanφ，其中φ为应变相对于应力的滞后角。内耗测量采用强迫振动模式，频率一般不大于［8］10Hz。实验参数为：振动频率0.015～4Hz，应变振幅35×10－6，升温速率0.25～12℃／min。

2 实验结果及分析

2.1 相变内耗与频率的关系

Cu－12Al－5Ni－1.6Mn－1Ti淬火态合金升温马氏体逆相变的内耗和相对动力学模量的温度曲线如图1所示，升温速率为1.5℃／min，测量频率为0.035～4Hz，在62℃左右出现内耗峰值并对应于动力学模量最小值，表明内耗峰是由相变过程中材料模量软化引起。

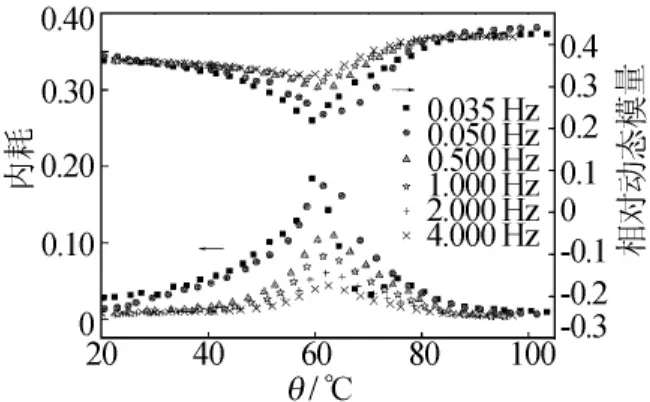
图1 相变内耗温度谱

对图1内耗曲线进行Gauss－Lorentz函数拟合，扣除内耗背底后，内耗峰值和对数频率的关系如图2所示。

当频率大于0.045Hz时，内耗峰值随对数频率的变化呈对称分布，这部分无法用Delorme－Belko模型解释的内耗是相界面滞弹性运动导致的模量软化所致；当频率小于0.045Hz时，内耗峰值和频率成反比，将其绘于倒数频率为横坐标的频率谱上则为直线（实线为拟合值），如图3所示，表明低于0.045Hz的内耗主要是由马氏体转变体积变化引起的。

图2 相变内耗和对数频率的关系

由图2拟合曲线可计算出1.5℃／min升温速率下的内耗半峰宽，从而得到相变弛豫时间τ＝1.031 8s和相变分布参数l＝0.617 4（定义为Debye内耗峰和实际内耗峰的半峰宽之比）。

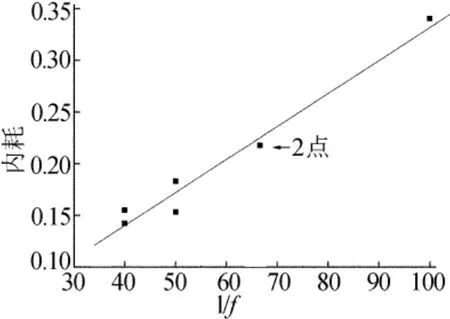
图3 相变内耗峰值和倒数频率的关系

2.2 相变内耗与时间的关系

热弹性马氏体相变弛豫时间是一个多变量函数，对升温速率尤为敏感。与Debye滞弹性弛豫的半峰宽对比，热弹性马氏体相变内耗的半峰宽略有增加，可以认为相变模量软化导致的弛豫属于滞弹性弛豫范畴。同样也可以将其他升温速率下马氏体逆相变的内耗和相对动力学模量的温度曲线转换成对数频率谱，计算出各自的内耗半峰宽及相变弛豫时间。合金在不同升温速率下的相变弛豫时间变化如图4所示。

图4 相变弛豫时间与升温速率的关系

由图4可以看出，随着升温速率的增加，相变弛豫时间开始迅速衰减，然后逐渐趋于一个稳定值。当 升 温 速 率 从 0.25 ℃／min 增 加 到12℃／min时，弛豫时间从 4.493 9s缩短到0.127 6s。

2.3 相变内耗与温度的关系

上述实验采用完全相变方法，即将合金加热到100℃母相状态，然后冷却转变为完全的马氏体，再升温测量内耗及动力学模量。在该条件下，升温时发生的马氏体逆转变量太多，马氏体片之间的距离太近，甚至相互接触，导致马氏体片之间的弹性应力场耦合强度高，相变时相界面切变阻力大，弛豫时间较长。

为了证实这种设想，本文实验采用部分相变方法，即首先根据合金的降温内耗峰温度范围（10～50℃）［9－10］预先设定一个温度θs，将合金加热至100℃保温30min使母相的组织结构达到稳定，然后缓冷至θs保温30min，最后从θs开始以不同的升温速率测量内耗和动力学模量。

Cu－12Al－5Ni－1.6Mn－1Ti合 金 的 母 相 属 于DO3有序固溶体，缓冷也能发生马氏体转变，而不会发生分解。缓冷的目的是减少内应力，使组织结构尽可能接近于平衡状态。部分相变测量时只允许发生较少的马氏体转变，故马氏体片之间距离较远，弹性应力场的耦合强度降低，马氏体片能以更加自由的方式形核及生长。θs越高，升温时马氏体逆转变量愈少，相界面运动愈容易［11］。

开始测量温度为42℃时马氏体逆相变的内耗和动力学模量温度曲线如图5所示，升温速率为1.0℃／min，测量频率为0.015～4Hz。对比发现，图5a出现2个内耗峰，对应于模量最小值的低温内耗峰PL和对应于模量拐点的高温内耗峰PH，它们分别起因于相变模量软化和相变体积变化。同样采用Gauss－Lorentz函数拟合将内耗背底扣除，并将低温内耗峰PL分离出来，则内耗峰值和对数频率的关系仍呈对称分布，计算出1.0℃／min升温速率下的相变弛豫时间τ＝1.313 6s和相变分布参数l＝0.745 7。θs＝42℃时相变弛豫时间随升温速率的变化曲线如图6a所示，当升温速率从0.25℃／min增加到4.3℃／min时，弛豫时间从4.527 9s缩短到0.353 8s。

为了比较θs的变化对相变弛豫时间的影响，θs＝48℃时测量的相变弛豫时间随升温速率的变化曲线如图6b所示，由图6b可看出，当升温速率从0.25℃／min增加到3.8℃／min时，弛豫时间从4.204 4s缩短到0.372 2s。

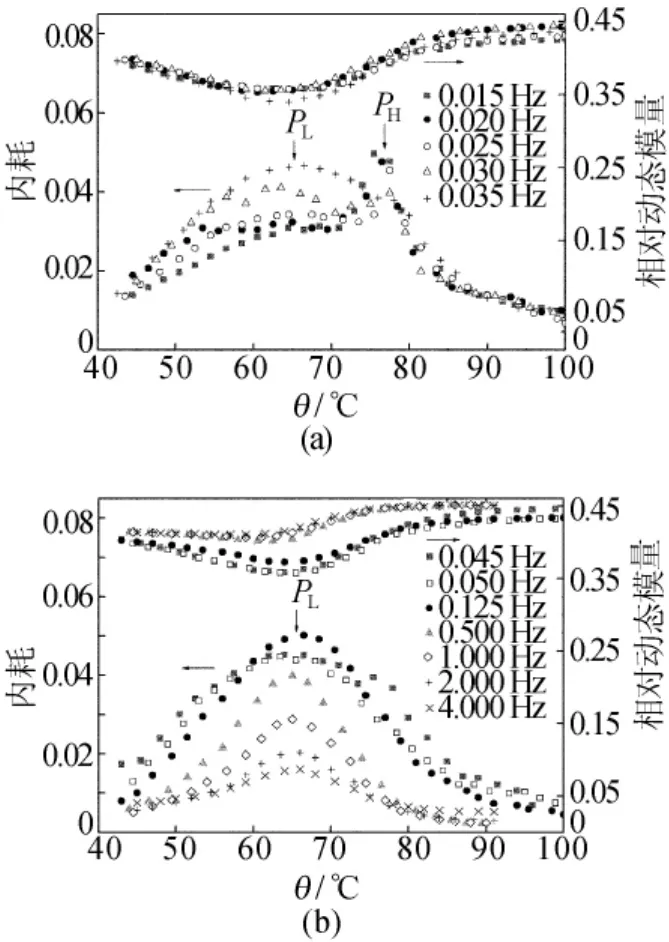
图5 不同频率下相变内耗温度谱

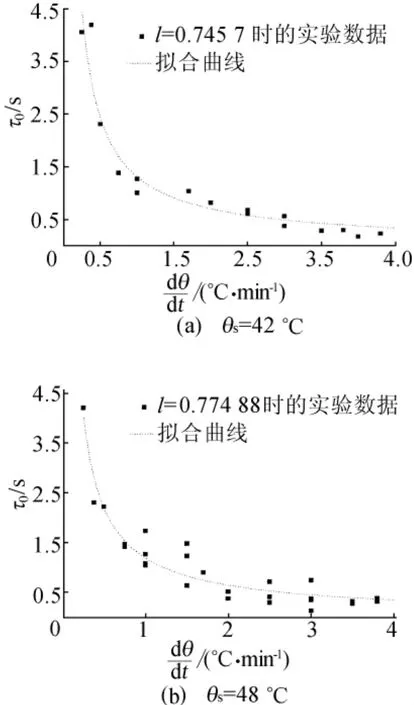
图6 不同θs时相变弛豫时间与升温速率的关系

完全相变、θs＝42℃和θs＝48℃时部分相变3种条件下，马氏体逆转变弛豫时间随升温速率的变化如图7所示。弛豫时间随升温速率的衰减可以解释为：随着升温速率的增加，合金的过热度增大，相变驱动力增大，使马氏体形核时间减小。当升温速率较小时，随着升温速率的增加，由于相变温度几乎不变（由内耗测量知，当升温速率小于2℃／min时，内耗峰位几乎不随升温速率变化），有效相变驱动力增大，使弛豫时间迅速减小；当升温速率较大时，增加升温速率的同时相变移向高温，出现明显的热滞现象，使有效相变驱动力非线性地增加，弛豫时间衰减变缓。在热弹性马氏体相变过程中，相变阻力包括弹性应变能、界面能原子微量扩散所需的能量［11］。随着升温速率的增大，相变驱动力不足以成比例地抵消相变阻力，导致相变滞后宽度加大，这是典型的形核－长大型相变的特征。

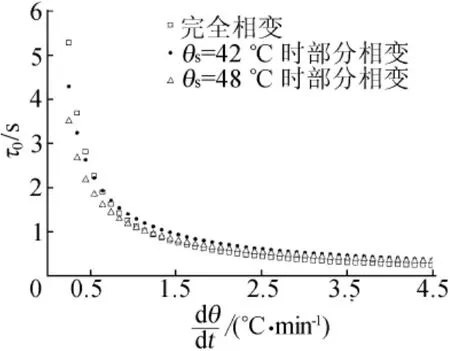
图7 马氏体量对弛豫时间和升温速率的影响

由 Fuoss－Kirkwood公式［5］得耗散模量为：

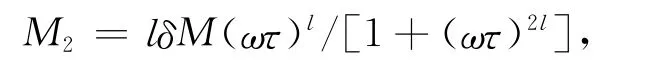
其中，ω为园频率；τ为弛豫时间；δM为弛豫量；l为分布参数。一般情况下，0＜l≤1。l＝1时 ，为理想的Debye弛豫，弛豫时间为恒定值；l＜1时，弛豫峰宽于Debye峰，此时弛豫时间并非常数，应视为连续分布函数。弛豫时间呈连续分布函数表明，即使在同一相变温度下形核时间也不同，马氏体在母相中的晶体学取向是影响弛豫时间的主要原因，也是影响马氏体相变可逆性的重要因素。

对比图7发现，相变分布参数l随θs升高而增大，并逐渐趋向于1，说明当马氏体转变量较少时，热弹性马氏体相变弛豫非常接近于Debye弛豫。

3 结论

（1）Cu－Al－Ni－Mn－Ti合金马氏体逆转变时，弛豫时间随升温速率的增大开始迅速衰减，当升温速率较大时，逐渐趋于稳定。

（2）合金的马氏体逆转变量越少，相变弛豫时间越短。完全马氏体逆相变时，升温速率从0.25℃／min 增 加 到 12 ℃／min，弛 豫 时 间 从4.493 9s缩短到0.127 6s；部分马氏体逆相变时，当开始测量温度θs＝42℃时，升温速率从0.25 ℃／min增加到 4.3 ℃／min，弛豫时间从4.527 9s缩短到0.353 8s，当θs＝48℃时，升温速率从0.25℃／min增加到3.8℃／min，弛豫时间从4.204 4s缩短到0.372 2s。

（3）合金的马氏体逆转变量越少，相变分布参数l越大，当θs较高时，l逐渐趋近于1。完全马氏体逆相变时，l＝0.617 4，部分马氏体逆相变时，当θs＝42℃时，l＝0.745 7，当θs＝48℃时，l＝0.774 9。

［1］Gastien R，Corbellani C E，Bozzano P B，et al.Low temperature isothermal ageing in shape memory CuAlNi single crystals［J］.Journal of Alloys and Compounds，2010，495：428－431.

［2］Montecinos S，Cuniberti A，Castro M L.Kinetics of isothermal decomposition in polycrystalline beta CuAlBe alloys［J］.Intermetallics，2010，18：36－41.

［3］Araki Y，Endo T，Omori T，et al.Potential of superelastic Cu－Al－Mn alloy bars for seismic applications ［J］.Earthquake Engineering ＆ Structural Dyanmics，2011，40：107－115.

［4］闵祥敏，宫晨利，吴青云.铜基形状记忆合金异常相变内耗的研究［J］.合肥工业大学学报：自然科学版，2009，32（1）：40－42.

［5］冯 端.金属物理学：第3卷［M］.北京：科学出版社，1999：7－37.

［6］Gong C L，Han F S，Li Z，et al.Two internal－friction peaks related to thermoelastic martensitic transformations in CuAlNiMnTi shape－memory alloy［J］.Physical Review B，2004，70：094103－094108.

［7］Gong C L，Han F S，Li Z，et al.Internal friction related to viscous motion of phase interfaces during thermoelastic martensitic transformation［J］.Philosophical Magazine，2007，87：2281－2297.

［8］Gui J，Zou W H，Wang R，et al.X－ray diffraction study of the reverse martensitic transformation in CuAlNiMnTi shape memory alloy［J］.Scrip Metall，1996，35：435－440.

［9］Nowick A S，Berry B S.Anelastic relaxation in crystalline solids［M］.New York：Academic Press，1972：90－198.

［10］Ratchev P，Van Humbeeck J，Delaey L.On the formation of 2Hstacking sequence in 18Rmartensite plates in a precipitate containing Cu－Al－Ni－Mn－Ti alloy［J］.Acta Metall Mater，1993，41：2441－2449.

［11］Zhang J X，Fung P C W，Zeng W G.Dissipation function of the first－order phase transformation in solids via internalfriction measurements［J］.Physical Review B，1995，52：268－277.