系列冲击试验转变温度的意义及其局限性

马 伟， 姜自强， 姜安婕

（1.合肥美亚光电技术股份有限公司，安徽 合肥 230088；2.安徽省电力科学研究院，安徽 合肥 230601；3.合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009）

1 转变温度曲线的数学模型及其特征

系列冲击试验可以揭示随着温度降低时，材质冲击韧性的变化趋势，更全面地反映了材质韧性特征，且因与断裂韧性试验、模拟实物工件的大型抗断试验相比，冲击试验简单实用、成本较低，累计数据和经验也颇为丰富，因而在机械、电力、桥梁、船舶，特别是核工业领域的设计制造、选材、安全控制等方面得到广泛的重视和应用［1－2］。系列冲击试验韧性测量值－试验温度表示的转变温度的典型曲线如图1所示。

图1 系列冲击试验韧性测量值－试验温度曲线

其中，冲击试验韧性测量值E指夏比冲击试验测得的体现韧性性质的参数，如冲击功Akv、冲击韧性akv、韧性断面率F、侧向膨胀值s等，ES、TS为曲线上指定点S的坐标。

由图1可见，转变温度曲线在高温侧有冲击试验韧性测量值水平段即上平台U，而在低温侧也有水平段即下平台L，中间段有下平台向上平台逐渐转变的区域，可称之为转变温度区。转变温度区的曲线呈现连续、单调递增的数学特征，其间存在拐点I。

工程上，习惯于采用某个指标（例如强度指标抗拉强度、塑性指标延伸率等）来评定材质的某种性能，因而也产生了理论上的转变温度指标，以期定量表征并可用以比较材料冲击韧性随温度变化出现的韧性变化特征。

但如上所述，冲击试验测得的体现韧性性质的参数有多种，而且转变温度的定义也有多种，不同行业、不同研究者因对各种转变温度的意义、价值、利弊认识程度以及经验积累程度不同而有着不同的偏好，其中，冲击功转变温度迄今仍有歧义，因此，对其进行深入分析和探讨并加以澄清显得十分必要。

迄今，国内外标准都没有从系列冲击试验测量数据求得转变温度的具体方法，美国标准ASTM A370给出了略微详细的原则性的规定［3］：若规定转变温度为达到某个测试值的温度，则在绘制的冲击值－温度最佳拟合曲线上，以图形内插（不许外插）的方式确定该曲线与规定测试值的交点为转变温度，并精确到3℃。有关标准也没有明确规定冲击试验转变温度曲线的物理计算模型，一直以来多采用手工绘制韧性测量值－温度曲线，主要依靠经验方法确定转变温度曲线的特征参数，例如上、下平台值及转变温度值。随着计算机技术的迅速发展，越来越多的研究工作者不再满足手工、经验且低效的方法，不断尝试用数学函数来模拟转变温度曲线，并采用非线性回归方法获得转变温度曲线的数学描述，例如采用局部线性、线性多项式、双曲正切函数的模型。从文献［4－8］来看，非线性数学函数模型——双曲正切函数模型得到较多的认同，该模型为：

其中，E为韧性测量值（Akv、akv、F、s）；T为试验温度；Emax、Emin分别为上下平台U和L的韧性测量值；Tc为曲线拐点的温度坐标；d为转变温度区间的度量。通过S形曲线拐点的切线方程为：

其中，（Emid，Tc）为S形曲线的拐点位置坐标，且Emid＝（Emin＋Emax）／2，Emid、Tc反映了转变温度曲线的位置特征，故可称之为位置参数。转变区韧性测量值区间理论长度为Emax－Emin，转变区温度区间理论宽度为4d。

过拐点的切线线段AB与上下平台构成转变温度曲线的简化形态。温度超过Tc＋2d，进入韧性测量值上平台区，温度趋向足够大时，E→Emax；而温度低于Tc－2d，进入下平台区，当温度足够低，E→Emin。即转变曲线理论上下平台分别是Emax、Emin，转变曲线温度区间上下界分别为Tc＋2d、Tc－2d。可见，Emax－Emin和4d决定了转变温度曲线的范围和形态，故可称之为形状参数。

位置参数和形状参数决定了转变温度曲线的全部特征，亦即揭示了材料的低温韧性特征。稍作变量替换容易证明，该模型的表达式为：

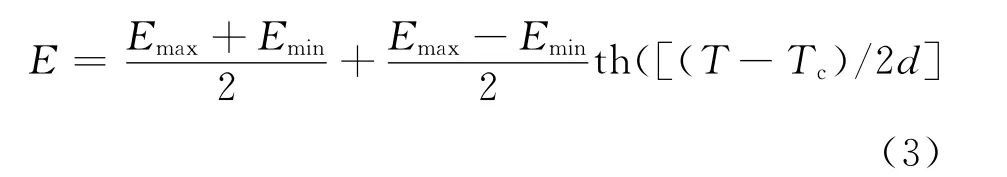
而转变温度的理论定义可以用该理论模型加以确定，例如，拐点位置温度坐标是一个理论转变温度，即Emid对应的转变温度，还可以通过（1）式方便地求得转变曲线上其他各特征点，任意韧性测量值ES对应的转变温度TS为：

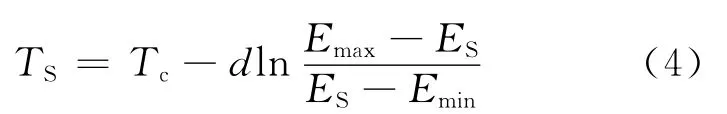
例如，韧性测量值为上平台1／2，即Emax／2对应的转变温度T0.5u为：

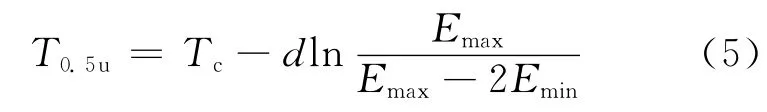
可见，同一模型（即同一材料）计算Emax／2对应的转变温度和Emid对应的转变温度有所不同，即：T0.5u≠Tc，当Emin＝0时，T0.5u＝Tc。

采用数学模型表达转变温度曲线，其各项特征参数可以从试验数据回归拟合获得，其物理意义也更为清晰，更容易定量分析各参数之间的关系，且计算规范、重复性好、可比性强，可以排除主观因素，使分析结果更为客观、科学。材质韧性水平由于材质类型（化学成分、热处理工艺）、受损伤程度及运行历史等因素的不同而存在差异，故根据上述理论模型，不同材质的转变温度曲线特征可以以转变温度曲线模型参数的变化或差异表现出来，大致可以分为几种典型类型，如图2所示。

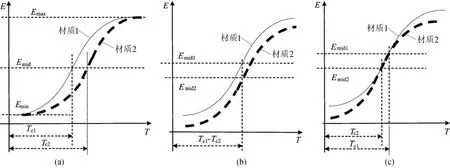
图2 转变温度曲线对理论转变温度影响模式的简化形态

其他变化可看作是简化的基本变化形态的组合，其结果导致更为复杂的情况。例如，下平台区域基本不变，上平台抬高；上平台区域基本不变，下平台抬高；上下平台之间区域出现交叉，如图3所示，图3中，TS1和TS2分别为材质1和材质2指定韧性测量值ES对应的转变温度。可见，在2种材质韧性水平相差不大的复杂情况下，只能在工作温度条件下进行局部比较才有实际意义。形状参数Emax－Emin和d变化不会出现负值，这是由转变温度曲线基本物理特性决定的。

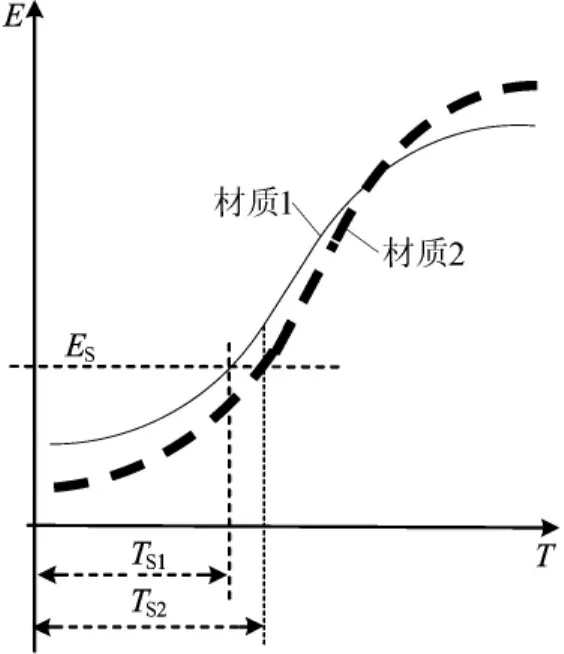
图3 转变温度曲线对理论转变温度影响模式的复杂形态

2 转变温度的定义及其意义

从上述转变温度特征曲线可知，所谓转变温度通常并非单一的临界值，而是一临界转变区域（Tmin～Tmax），很显然，若要比较不同材料的材质韧性水平，直接比较其完整转变曲线最为合理，如图2～图3所示。鉴于上述转变温度曲线变化的复杂性，理论上表明2种不同材质的韧性显得十分必要。

根据冲击韧性与断裂破坏性质的对应关系，不同韧性材质的韧性水平高低应当符合如下基本原则：① 相同工作温度下，具有高的冲击韧性试验值的材质为韧性较高；② 相同韧性水平下，具有较低的对应温度的材质为韧性较高。

图1所示的转变温度曲线中，指标定义（韧性测量值类型以及规定数值）不同，定义并确定转变温度的类型也不同，转变温度的定义以下几种：文献［9］定义为吸收能量突变，且韧性和脆性断裂模式互相转变时对应的温度；文献［3］中转变温度是指在这一温度时，所设定的材料的试验值等于或超过所规定的最低试验值，在其附录中还给出其他几种转变温度的定义；文献［10］中称其为指标转变温度，由最佳拟合的夏比冲击试验转变温度曲线获得的与预先设定的吸收功、侧向膨胀值或韧性断面率所对应的温度。

文献［11］中给出的规定转变温度的几种判据为：① 冲击吸收能量达到特定值时所对应的温度；② 冲击吸收能量达到上平台某一百分数（n%）所对应的温度；③ 剪切断面率达到某一百分数（n%）所对应的温度；④ 侧膨胀值达到某一量所对应的温度。

纵观各种转变温度的定义和确定方法，都试图从转变温度曲线上规定某一特征转变点。而不同类型韧性试验值－温度曲线形状相似，但其上的特征点又具有不同的力学意义。实践表明，转变温度与对应指标的定义有关，故不同定义的指标对应的转变温度数值也不同，力学意义也有区别，故不可以相互比较。依据韧性指标与材料自身性质的关联，与转变温度对应的韧性指标大体可分为2类：

（1）相对指标转变温度。转变温度所对应的韧性指标因材质不同而异。其特点是，转变点的韧性指标数值与转变温度曲线上下平台有直接关联，而且因为不同材质的同一转变温度曲线的冲击功上下平台水平也是不同的，互相比较的材料的转变温度对应韧性指标实际上并不相同。本文称其为相对指标转变温度，即冲击功上下平台平均值对应的转变温度，或者是冲击功上平台50%对应的转变温度［11－12］。

（2）绝对指标转变温度。转变温度所对应的韧性指标与材质没有直接关联，而是人为规定的，互相比较的材料的转变温度对应韧性指标相同。因而，相对于上述类型，此类定义的转变温度可称为绝对指标转变温度。对于不同的材质上平台的韧性断面率均为100%，该数值并不因材质的不同而不同，故按文献［11］中规定的第3条所得断口形貌转变温度FATT，实际上属于绝对指标转变温度类型，而不属于相对指标转变温度。

对于塑性指标的侧向膨胀率，理论上存在转变温度曲线的上平台，但在实践中并没有使用侧向膨胀率上平台某一比例值作为转变温度指标。

相对指标转变温度和绝对指标转变温度，在工程实践中具有不同的功能和表现，正确认识其中的力学含义，具有重要意义。

在图2a中，由于形状参数Emax－Emin、d以及位置参数（Emax＋Emin）／2不变，所以韧性测量值上下平台值Emax、Emin均不变，仅发生图形平移。如果进行比较的2种材料的转变温度曲线特征符合这些特征，用各种类型定义的转变温度进行比较，均不会出现歧义。一般而言，冲击试样韧性断面率在高温时等于或接近100%，而在低温时则接近于0，随材质的不同，这一现象却大体相同。因此，通常采用韧性断面率作为韧性测量值指标时，就属于这种情况。

而对于图2b、2c的情况，则不然。在图2b中，形状参数Emax－Emin、d以及Tc不变，（Emax＋Emin）／2发生变化，若设拐点纵坐标位置原来为a，现变化ΔE，则：

而假定形状参数保持不变，即Emax－Emin＝2b，故连列求解的结果为：

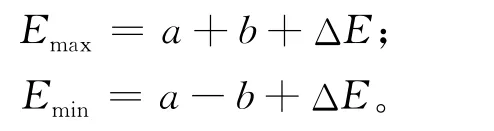
这意味着，图2b的情况材质韧性水平发生了变化，但其转变温度却未变。如果把图1中的斜向直线段AB近似视为转变温度曲线，则（Emax＋Emin）／2实际上为转变温度区间的平均韧性。但该转变温度用于比较材质低温韧性会发生失灵。

转变温度作为低温韧性指标的本意，应当是低温韧性较好的材料，其转变温度也较低。但事实上，转变温度对应的韧性指标是材质自身上下平台之1／2位韧性指标，即Emid＝（Emax＋Emin）／2。由于转变温度曲线单调递增，当Emid增大时，其相对指标转变温度Tc也增大，与转变温度的本意相违背，如图2b所示。根据相对指标转变温度定义，材质韧性提高（上平台提高、下平台提高或两者均提高），其转变温度上升，这与转变温度下降体现韧性提高的基本特性相反，如图2c所示。

出现以上情况的原因在于，该转变温度所对应的韧性测量值与测试材料韧性是相关联的，而不同材料有不同的值。而对于绝对指标转变温度，不同材料的转变温度对应相同的韧性测量值基准，其转变温度趋势和材质韧性趋势始终保持一致，故不会发生上述失灵情况。可见，相对指标这种转变温度定义的韧性值的相对性，导致了该转变温度的不合理性。上述分析从理论上揭示了相对指标转变温度定义的缺陷。

同时，默认冲击功－温度转折区下平台存在理论假定［4］Emin＝0也不尽合理。首先，该转折区下平台能量数值一般为裂纹形成功，而V型缺口的夏比冲击试样裂纹形成功［13］一般不为0；其次，因不同材质，该下限温度对应的冲击功数值并不相同，而且下限冲击功数值对缺口尖锐度等试验条件极为敏感，所以零塑性转变温度与冲击功－温度曲线下平台转折区并不构成严格对应［14］。

3 相对指标转变温度的不合理性分析

以28CrMoNiVE等3种材料［15－16］各有2组系列冲击试验数据为例，采用（1）式表示的非线性数学函数模型——双曲正切函数模型计算系列冲击试验冲击功指标转变温度作进一步分析，非线性回归计算采用Origin程序，结果见表1、图4所示。

4种定义的冲击功转变温度TS见表1所列，其中规定冲击功为Emin和Emax／2为相对指标，规定冲击功为41J和68J为绝对指标，同时还给出剪切断面率为50%时的断口形貌转变温度FATT50的计算结果和原文献提供的FATT50数据。

采用（1）式即可对系列冲击试验测量数据ET进行回归计算，从而获得表征转变温度曲线的4个参数。但非线性回归结果不可做超出试验数据的外推，否则容易导致大的误差甚至谬误，而通常系列冲击试验测量数据很难完全覆盖转变温度曲线各个部分（上下平台及整个转变区），否则会导致边界参数Emax、Emin超出试验值而产生外推，易对接近上下平台区域的部分导致较大误差，这对于取与上下平台关联比例值为指标的转变温度的计算会产生极大连带误差。

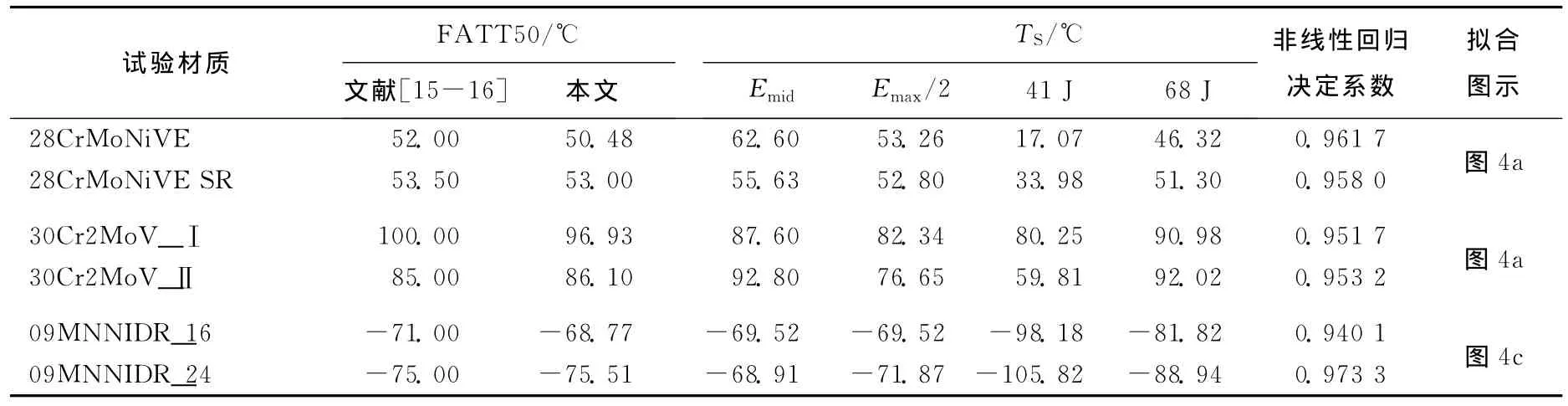
表1 几种材料的冲击功－温度试验数据非线性回归计算结果

图4 冲击功－温度试验数据非线性回归计算及拟合结果

鉴于上述理由，本文参照ASTM E185－2002，冲击功上平台数值Emax通过物理原理确定，即由韧性断面率为100%所对应的冲击功测量值确定，作为（1）式的已知参数；而下平台Emin以及Tc、d则由（1）式回归计算得到，以获得实验数据区域的最佳拟合。

由表1和图4可知，采用冲击功（或冲击韧性）上下平台之间的1／2位作为转变温度指标，计算所得转变温度出现了与实际低温韧性趋势相反的结果。

由图4a可知，28CrMoNiVE韧性优于28CrMoNiVE SR，作为表示低温韧性特征的转变温度，应当是28CrMoNiVE的转变温度低于28CrMoNiVE SR。计算所得FATT较好地反映了两者的区别，但冲击功（或冲击韧性）上下平台之间的中位计算所得的28CrMoNiVE＿SR的转变温度反而低于28CrMoNiVE。

采用上平台1／2为指标的转变温度则出现明显改进。如果把2种材料的转变温度计算值之差作为分辨率，其分辨率仍然较小，明显不如断口形貌转变温度FATT50，以及规定冲击功水平为指标的转变温度。

这表明，以冲击功相对指标定义的转变温度存在明显的不足。特别是冲击功（或冲击韧性）上下平台之间的1／2位定义的转变温度，容易出现失灵甚至误判。而绝对指标转变温度，大多处于试验数据范围以内，无论何种拟合方法，都属于内插，误差较小，可以很好地反映材质低温韧性的客观差别。

上述3个实例计算结果还表明，采用（1）式模型计算转变温度，由于模型统一、计算规范，试验数据利用率高，明显提高了转变温度计算值分辨率。采用冲击功上平台1／2位为指标的转变温度，还必须保证试验数据冲击功最低值小于0.5倍上平台值，否则无法得到结果，或外推产生。

综上所述，采用冲击功、侧向膨胀率构成的转变温度曲线是由技术手段测量所得，客观性较好，采用绝对指标定义转变温度，可客观合理地揭示材质低温韧性。但规定指标水平可能须因材质不同而作调整，而无法完全统一。而相对指标定义的转变温度可作为不同材质的统一规范，但也存在某些失灵的情况，在实践中值得关注，应予以避免。韧性断面率定义的转变温度（如FATT）属于绝对指标转变温度，测试数据符合韧性脆性的本意，可客观合理地揭示材质低温韧性，但韧性断面率的测定，虽已有较为成熟的规范，但仍存在易受主观影响的因素。故工程实践中，在给出试验数据及转变温度曲线的基础上，采用2种以上的指标转变温度对不同材质进行比较。

事实上，现行法规都规定了绝对冲击值定义的转变温度，各国规范大体一致，其意义理解也较为一致，其绝对值多基于经验统计而有一定差异，其中美国ASTM标准的规范数值应用较广。而相对冲击值定义的转变温度尚存在一定分歧。

文献［10］规定对于辐照脆化的比较，必须同时比较规定冲击功对应的温度以及上平台冲击功值，而没有采用Emid或Emax／2所对应的转变温度指标。文献［10］实际上是就2种材料转变区域的大部分进行了比较，因此，有其明显的合理性。

4 结论

（1）双曲正切函数模型用于回归拟合冲击值－温度转变曲线，简单明了，规范性、重复性好，误差小，工程上用于计算并分析转变温度曲线优点明显。

（2）现有若干转变温度的定义各有特点，工程上只有相同定义的转变温度方可比较。无论采用何种定义或判据，得出的转变温度用于比较不同材质的低温韧性，必须符合本文提出的2个基本准则：① 相同工作温度下，具有高的冲击韧性试验值的材质为韧性较高；② 相同韧性水平下，具有较低的对应温度的材质为韧性较高。

（3）提出指标转变温度的相对性概念。通过理论分析和实例计算证明，相对指标转变温度用于比较不同材质的韧性水平存在明显不足。例如采用相对冲击功为指标的转变温度比较材质韧脆转变性能存在谬误的可能，在科学研究和工程验收等实践应用环节中必须慎重抉择。在重要场合，应用相对指标转变温度应以其他指标补充或辅助验证。ASTM E185采用同时比较规定冲击值对应的温度和上平台冲击功水平的方法，有其明显的合理性。

［1］周惠久，黄明志.金属材料强度学［M］.北京：科学出版社，1989：216.

［2］肖纪美.金属的韧性与韧化［M］.上海：上海科学技术出版社，1982：58.

［3］ASTM A370－09，Standard test methods and definitions for mechanical testing of steel products［S］.

［4］张 峥.钢的韧脆转移过程的数学仿真及其冷脆断裂的定量诊断方法研究［J］.中国机械工程，1992，3（2）：3－6.

［5］钱维平，蒋和岁.工程结构用钢温度转变特性的表征及其应用［J］.材料开发与应用，1997，12（1）：2－6.

［6］黄 强.核用压力容器钢冲击转变曲线数学模型的建立及程序设计［J］.成都科技大学学报，1995（1）：60－64.

［7］Miannay D P.Time－dependent fracture mechanics［M］.New York：Springer，2001：5

［8］Tanguy B，Besson J，Piques R，et al.Ductile to brittle transition of an A508steel characterized by Charpy impact test，Part－Ⅰ：experimental results［J］.Engineering Fracture Mechanics，2005，72：49－72.

［9］GBT 10623－2008，金属材料力学性能试验术语［S］.

［10］ASTM E185－2002，Standard practice for design of surveillance programs for light－water moderated nuclear power reactor vessels［S］.

［11］GB 299－2007，金属材料 夏比摆锤冲击试验方法［S］.［12］GB 299－1994，金属夏比缺口冲击试验方法［S］.

［13］涂铭旌，鄢文彬.低合金钢低温脆性断裂论文集［C］.西安：西安交通大学出版社，1985：70.

［14］Pellini W S.结构完整性原理［M］.周黻秋，王克仁，译.北京：国防工业出版社，1983：78.

［15］火力发电厂金属材料手册编委会.火力发电厂金属材料手册［M］.北京：中国电力出版社，2001：4

［16］滕明德，顾先山.09MNNIDR钢板及其焊接接头的低温韧性试验研究［M］.压力容器，1992，9（4）：8－13.