鞋楦数字模型的特征识别与自动提取

胡小春， 翟亚磊， 周福静

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

0 引言

我国是世界上最大的鞋类和鞋用附件的生产国和出口国。企业要在激烈的市场竞争中形成有竞争力的品牌，就要提高产品的快速设计及制造能力，要在短时间内推出时尚新样式，快速获取鞋楦数字化模型并成型是其核心环节［1］。基于逆向工程技术的鞋楦快速成型技术是满足人们这种追求的首选途径［2］，即首先对鞋楦进行激光扫描获取鞋楦的点云数据，然后通过对获取的数据模型进行缩放和修改处理建立新的鞋楦数据模型［3］。由于基于密集数据的鞋楦模型不利于后期的尺码缩放和个性化修改［4－6］，为此，对鞋楦数据模型需要进行基于特征的参数化建模。目前一般建模方法都是通过手工选择或者删除点，然后确定某些特征点，拟合特征曲线，最后构建曲面［7］。对于鞋楦这样的产品，由于尺寸很多、款式层出不穷，其逆向建模过程中有些步骤应遵循一些规律实现自动化，这将促进不同鞋楦模型的收集和利用、促进鞋楦设计生产自动化。

有效、快速提取鞋楦主要特征及特征值对于鞋楦数字化技术快速发展具有重要意义。越来越多的学者也开始从事这方面的研究，如文献［8］提出了鞋楦曲面数字化特征信息识别法；文献［9］进行了基于二阶差分的方法对鞋楦底部棱边提取与底面展平的研究；文献［10］用三次光顺样条函数和二阶光顺样条滤波泛函约束指标对测量的鞋楦曲面数据进行预处理和光顺，利用微圆弧逼近曲线曲率半径进行楦曲面特征点的提取；文献［11］利用鞋楦表面曲线的切线的斜率来识别楦底拐点，进而得到楦底样轮廓。

这些研究主要集中在鞋楦楦轮廓的提取和楦曲面测量数据处理以及特征点的提取，对鞋楦的其他主要特征没有涉及。为了实现鞋楦的参数化建模，根据有关鞋楦设计手册［12］，应该以前跷高、后跟高这2个特征为主控参数对中轴线上的主要特征点进行控制，从而实现楦底的参数化建模；以跖围、跗围、兜围三围线这几个特征为主控参数对楦表面各楦高进行控制来实现对楦面的参数化建模。

本文利用Matlab软件及C语言编写程序对采集到的点云数据进行编程处理［13－15］，首先进行了鞋楦方位的标准化，在此基础上实现上述鞋楦主要特征的自动提取。鞋楦主要特征及特征值的提取，可为后期鞋楦数字化模型的建立及鞋楦表面的局部修改打下较好的基础。

1 鞋楦数据模型方位的标准化

采集的鞋楦三维数据模型是由一圈一圈的扫描点组成的，通常不是按标准方位放置的，如图1所示。根据鞋楦设计手册，必须将鞋楦模型旋转到标准方位放置，才能有利于鞋楦主要特征及特征值的提取。

从图1可以看出，需要对模型进行以下处理：翻转180°的变换、求鞋楦楦底样的标准长度、显示前跷高和后跟高的变换、鞋楦纵切面与yOz面平行的变换。

图1 鞋楦点云模型初始位置

对于任意一个三维坐标点P（x，y，z），绕x轴旋转任意α角，得到点P1（x1，y1，z1）。P点用柱坐标表示为x＝x，y＝rsinθ，z＝rcosθ，则P1点的坐标为：

用矩阵可表示为P1＝PT，其中：

1.1 翻转180°的变换

将图1所示的模型与鞋楦设计手册中标准位置相比较可知，需将其绕x轴逆时针翻转180°，得到图2所示方位。这里的变换矩阵T见（4）式，其中α＝180°。点云数组AL为3列矩阵，每列分别对应点的x、y、z值。在Matlab中处理时，将x列存于数组AL1，y、z列存于数组AL2，仅对AL2实行变换：

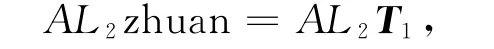
其中，T1是T的子矩阵，即

将AL1和AL2zhuan水平连接可得到翻转后的点云数据，翻转后的数据导入到Pro／E中得到如图2所示的鞋楦模型。

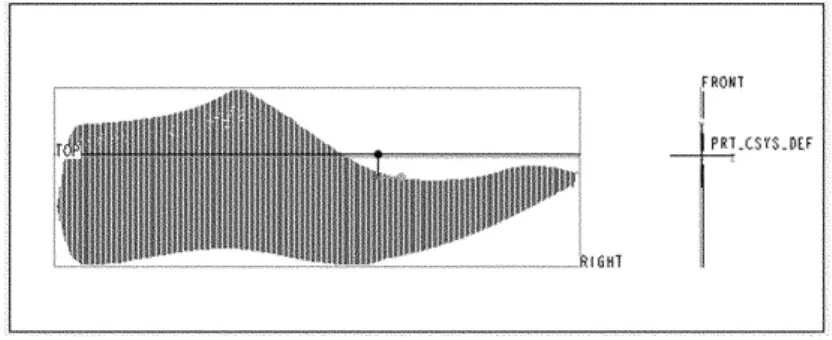
图2 点云模型翻转180°后的模型

1.2 求鞋楦楦底样长

楦底样长是鞋楦设计中的主要参数，与脚长、楦的尺寸都有关联。不同的鞋头会影响楦的实际长度，在鞋楦设计标准中［16］，楦底样长是指具有基本鞋头（素鞋头）的鞋楦楦底样长度。本文的鞋楦为一男式尖头鞋楦，其实际楦底样长大于基本楦底样长。

为了正确提取鞋楦主要特征，需先求出鞋楦的楦底样基本长度。根据鞋楦的设计标准，有以下关系：

其中，通常取后容差为5mm，放余量为20mm。

从鞋楦数据模型可求出L2和L3，根据（5）式和（6）式求出脚长，再求出楦底样长L。本文中实际楦底样长L1、L2、L3分别为289.28、177.63、153.82mm，将L2、L3分别代入（5）式、（6）式中可得脚长数值分别为251.903、250.11mm，由鞋楦设计手册中脚的基本长度可知，该鞋楦模型所对应的脚长为250mm。将其值代入（7）式中，可得楦底样的标准长度为265mm。实际楦底样长L1比标准楦底样长L长了24.276 5mm。

1.3 显示前跷高和后跟高的变换

图3所示模型为设计手册中标准方位放置，能直观地反映出鞋楦前跷高和后跟高的关系。要将图2中的模型旋转到这种标准方位，需绕x轴顺时针旋转一个角度α，其值由前跷高和后跟高的关系来确定。

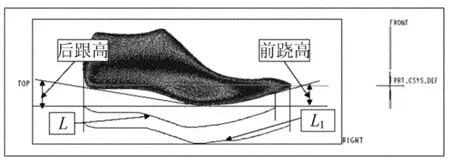
图3 前跷、后跟高及L、L1示意图

由鞋楦设计手册可知后跟高的变化遵循高度等差规定，男鞋后跟高的高度等差为5mm，女鞋为10mm，并且男女鞋前跷与后跟高关系的数学表达式为：

图2模型旋转α角后，其前跷高与后跟高必须满足表达（8）式。

在求前跷高与后跟高时，需按照设计手册中基本楦底样长度即是L的长度进行求值。前跷高是标准楦底样的前端点与前脚掌着地点的高度差计算，这个端点不是鞋楦数据模型的前端点，如图3所示。

后跟高就是后跟点与前脚掌着地点的高度差，（8）式的前跷高和后跟高的关系可用来判断鞋楦模型的放置方位是否合适。由于x坐标不变，仍然抽取数组中后2列［y，z］来进行旋转变换，以求使模型满足（8）式。

该步的编程思路是：首先确定后跟点即后跟处高度最低点，对模型的（y，z）坐标进行旋转的角度α在5°～15°范围之内。从5°开始，旋转角度α每次递增0.1°。每次对模型进行旋转变换后，这个新数组中高度最低的点就是前掌着地点，原后跟点在旋转后也有了新的坐标值。计算新的前跷高和后跟高，然后判断是否满足（8）式，直到满足条件为止。

求绕x轴旋转角度的程序流程，如图4所示。

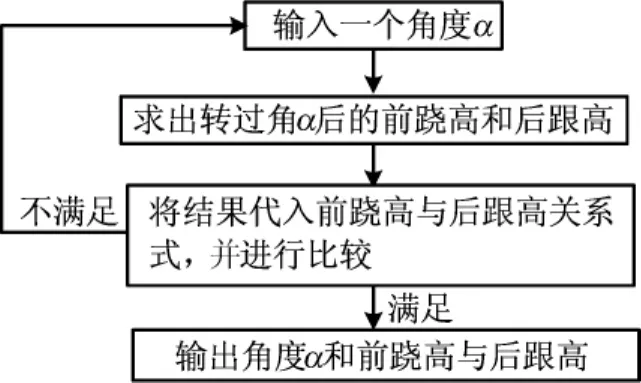
图4 求绕x轴旋转角度的程序流程图

程序运行结果是：绕x轴顺时针旋转9.4°时，前跷高为16.910 4mm，后跟高为25.04mm，所得的值满足（8）式。

1.4 鞋楦纵切面与yOz面平行的变换

鞋楦的纵切面一般为过楦头端点P2和楦尾端点P3的一个平面，并且垂直于楦底面。在标准的鞋楦放置方位，这个切面经过或平行yOz面，因此其上2点P2和P3的x轴坐标值应相近或相等。

鞋楦纵切面与楦底面相交形成的曲线就是楦底中轴线，这是鞋楦设计的一个重要特征。

首先找楦头端点P2和楦尾端点P3，这2点应在鞋楦模型两端的数据点环上，分别是数据环上y坐标值最小的点。据此提取的2个端点坐标值分别为P2（－5.7，12.3，70.485）、P3（－13.1，27.9，358.765），它们的x坐标值相差比较大，说明实际的纵切面与yOz面不平行，因此要将鞋楦模型绕y轴旋转，旋转的角度β可由三角关系式求出：

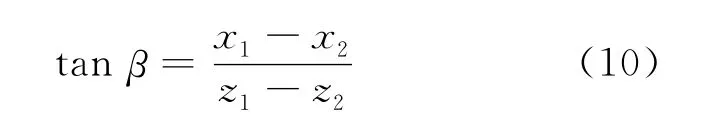
其中，x1、z1为P2点的x、z坐标值；x2、z2为P3点的x、z坐标值。求出旋转角度β＝－1.47°。旋转之后的楦头楦尾端点的x坐标很接近，楦头端点x、z坐标为（－3.889 9，－70.608 0），楦尾端点x、z坐标为（－3.892 1，－358.983 0）。绕y轴顺时针旋转1.47°后的数据模型导入Pro／E中，如图5b所示。

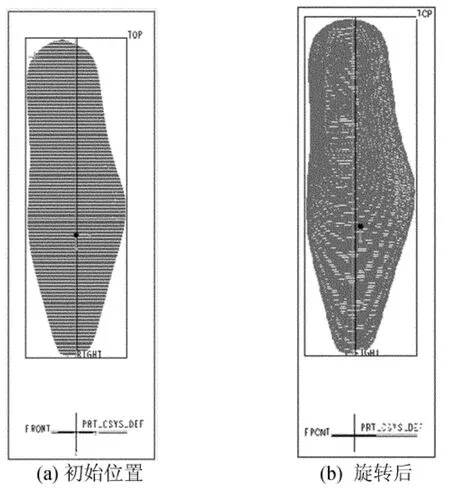
图5 绕y轴旋转1.47°后的对照图

2 鞋楦几何特征的自动提取

本文讨论的鞋楦几何特征主要包括：中轴线、楦底轮廓线和跖围、跗围、兜围三围线。这些特征从经过前述几种坐标变换、按标准方位放置的鞋楦模型中提取，利用Matlab软件编程自动提取前2个鞋楦几何特征；利用C语言编程来提取三围线的点云数据，将其导入Pro／E中生成三围线并在其基础上测量出其长度。

2.1 鞋楦模型中轴线的提取

中轴线是纵切面与鞋楦模型相交的线。鞋楦模型在纵切面x＝－3.89上的交点可能比较稀疏，所以提取纵切面附近－3.99＜x＜－3.79的所有点，其x坐标均用x＝－3.89代替，可得到一条较密集的中轴线。其编程思路为：让鞋楦数据中x坐标值在－3.99＜x＜－3.79范围内的点保存下来，其x坐标均用x＝－3.89代替，所保存的数据就是要提取的中轴线的数据，将程序运行结果的数据导入Pro／E中，如图6所示。

图6 构成中轴线的点

2.2 楦底轮廓线的提取

鞋楦底面是一个比较复杂的曲面，将其垂直投影就可以得到完整的楦底平面。在Pro／E中，从俯视图方向看，能够看到完整底面轮廓。因此只要找出每个点云环x坐标值最大和最小的点，即可以提取出楦底外轮廓的轮廓点。将得到的底面轮廓点数据导入到Pro／E中可以得到底面轮廓的形状，如图7所示。

图7 构成楦底轮廓的点

2.3 鞋楦模型三围线的自动提取

跖围是楦的第1跖趾内宽点与第5跖趾外宽点间的围长；跗围是楦腰窝外宽点绕过楦背一周的围长；兜围是楦底后跟端点绕过楦背一周的围长。由于点云数据体现了鞋楦的表面特征，而三围线也都是鞋楦表面的线，三围线的自动提取就是在一个曲面上提取几条曲线。

2.3.1 处理思路

首先在鞋楦模型的3个围度处建立3个平面与鞋楦数据模型相截，所得到的截线就是3个围线。考虑到鞋楦模型上与截平面上相交的数据点可能较稀疏，所以将截平面两侧距截平面距离d小于一定值b的数据点形成一个点云带，这些点云带在截平面的投影可以看成是鞋楦模型上与截平面上相交的数据点，这就增加了所求围线的数据点密度。为了更精确地提取三围线，利用点到平面的距离d小于特定条件（这里的r为鞋楦最大极半径的估计值）来判断鞋楦数据模型中的数据点是否在三围线的点云带中。

2.3.2 截平面方程的确定

通过跖围的截平面方程，由跖围的概念可知过跖围的截平面必通过以下3点：第1跖趾内宽点、第5跖趾外宽点及这2点在z轴方向的中点（z轴是鞋楦的长度方向，在中点的点云环中取y坐标值最大的点），根据这3点来确定过跖围的平面。由前面3个点的坐标，利用Matlab编程求出通过跖围的截平面方程为：

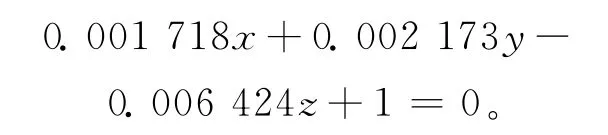
用同样的方法可以求出通过跗围及兜围线的截平面方程分别为：

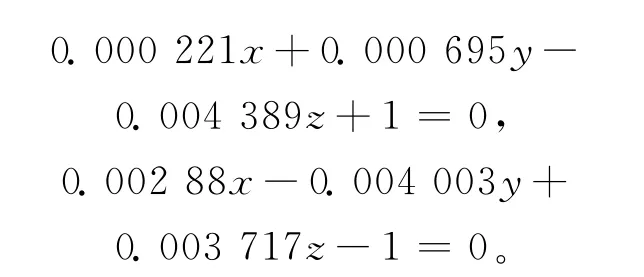
2.3.3 三围线点云数据的提取

根据已求出所通过3个围线的截平面方程，考虑到提取底面轮廓时Matlab程序比较复杂，该步利用C语言编写程序对数据进行处理，求出三围线的点云数据，其程序流程如图8所示。

将程序处理的数据导入到Pro／E中，用样条曲线将这些点连接起来可得到所求三围线，如图9所示。经测量跖围与跗围、兜围的长度分别为L1＝236.641mm，L2＝246.099mm、L3＝338.914mm。而鞋楦设计手册中标准长为L1＝239.5mm，L2＝243.5mm，所提取围线的长度与标准长度的差值在所允许的设计误差±3.5mm范围内，故所提取的数据是正确的。

图8 三围线数据提取的程序流程图

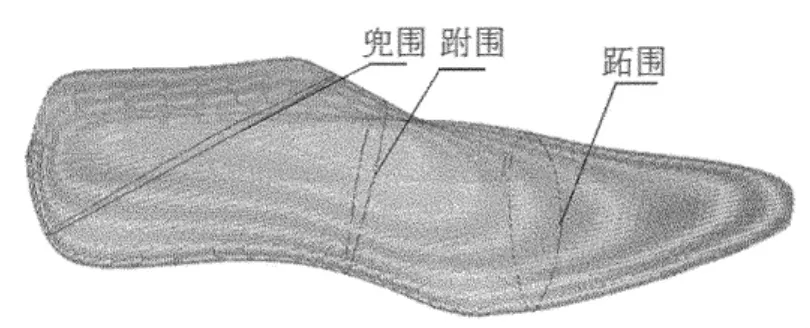
图9 提取的三围线

3 结束语

基于密集数据的鞋楦模型不利于后期的尺码缩放和个性化修改，因此需要建立鞋楦数字模型的特征模型。本文基于逆向工程，对采集的鞋楦原始数据进行处理，通过编写程序来自动化提取出鞋楦的前跷高、后跟高、中轴线、楦底轮廓及三围线的主要特征，这有利于鞋楦数字化设计及个性化设计。

对于提取的点云数据处理还不够精确，还需进一步地精确处理去除杂质点，以便于提取的数据生成光顺圆滑的曲线。

［1］陆国栋，陈 健，王 进.基于CAD／CAM 集成的鞋楦快速逆向成型技术研究［J］.计算机应用技术，2006（9）：28－30.

［2］孙福辉，席 平，唐荣赐.复杂产品集成逆向工程系统及其关键技术［J］.北京航天航空大学学报，2001，27（3）：351－355.

［3］陈俊华，辛 勇.基于CAD／CAM软件的鞋楦逆向设计与制造［J］.制造业自动化，2007（3）：82－84.

［4］万孝军.基于逆向工程鞋楦参数化建模及其修改技术研究［D］.合肥：合肥工业大学，2009.

［5］罗 胜.鞋模数字化技术的现状和各种方法的对比［J］.轻工机械，2007（6）：5－9.

［6］胡小春，王 刚，万孝军.基于足底压力分布的鞋楦参数化设计［J］.合肥工业大学学报：自然科学版，2011，34（2）：180－183.

［7］陈 翔，张 欣.逆向工程在鞋楦自由曲面重建中的应用［J］.西安工程科技学院学报，2005，19（2）：228－232.

［8］刘 冬，林述温.鞋楦曲面数字化特征识别与数据压缩［J］.华侨大学学报：自然科学版，2003，24（1）：76－79.

［9］胡安铎，苏显渝，刘成林.鞋楦底部棱边提取与底面展平［J］.四川大学学报：自然科学版，2009，46（2）：382－386.

［10］李儒琼，董淑冷，李光布.鞋楦扫描数据预处理和特征点提取［C］／／中国机构与机器科学应用国际会议，上海，2007：77－80.

［11］刘成林，苏显渝，胡安铎.鞋楦楦底轮廓提取及展平［J］.激光杂志，2008，29（6）：45－46.

［12］孙 毅.中国标准鞋楦设计手册［M］.北京：中国纺织出版社，2008：6－63.

［13］林 雪，松周婧，林德心.Matlab7.0应用集锦［M］.北京：机械工业出版社，2005：15－40.

［14］飞思科技产品研发中心.Matlab 7基础与提高［M］.北京：电子工业出版社，2005：22－46.

［15］谭浩强.C语言程序设计［M］.北京：清华大学出版社，2000：38－66.

［16］范成杰.鞋楦底样设计方法［J］.中国皮革，2007，36（18）：171－173.