C-余弦算子函数拓扑
毕 伟,赵华新
(延安大学 数学与计算机科学学院,陕西 延安 716000)
C-余弦算子函数拓扑
毕 伟,赵华新
(延安大学 数学与计算机科学学院,陕西 延安 716000)
利用 C-余弦算子函数的概念,引入一新的局部凸向量拓扑,并对其基本性质以及在新的局部凸线性拓扑意义下 C-余弦算子函数的性质进行初步研究。
余弦算子函数;局部凸向量拓扑;生成元;C-余弦算子函数拓扑
2006年赵华新[1]首次提出了半群拓扑这一理论,之后王晓梦[2]将这一理论推广到积分 C-半群拓扑。本文在此基础上,主要利用 C-余弦算子函数的概念,诱导出一新的局部凸线性拓扑,并对其基本性质以及在新的局部凸线性拓扑意义下 C-余弦算子函数的性质进行初步研究。余弦算子函数拓扑将局部凸线性拓扑空间理论与有界线性算子半群理论有机地结合起来,使这两个方面的理论更为丰富,应用更为广泛。
设X是Banach空间,C∈B(X)是一单射,强连续算子族{T(t),t∈R}∈B(X)是 X上的 C-余弦算子函数,即满足:
(1) T(0)=C;
(2)2T(t)T(s)=T(t+s)C+T(t-s)C t,s∈R.
C-余弦算子函数{T(t),t∈R}的无穷小生成元 A定义如下:Ax=(λ2-C)x,∀x∈D(A)={x∈X;Cx∈R(Rλ)}
其中 Rλ=λ-1e-λtT(t)dt∈B(X),(λ>ω)为单射,且A与 λ无关。
A的 C预解式定义如下:
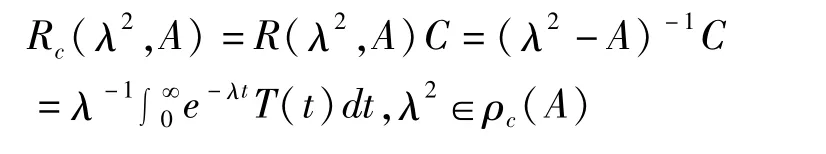
其中 ρc(A)={λ2:λ2-A为单射且 R(C)⊂R(λ2-A)}。
对任意λ>ω,令 Rλ(x)=‖R(λ2,A)cx‖=
x∈X,t∈R,则利用C-余弦算子函数的定义容易验证,对任意 x,y∈X及 λ>ω有
(1)pλ(x)≥0;
(2)pλ(x+y)≤pλ(x)+pλ(y),x,y∈X;
(3)pλ(αx)=αpλ(x),α≥0.
即 Pλ(x)是X上的一半范数,从而由半范数族 S={Pλ,λ>ω}可以确定一局部凸向量拓扑,记为 τ。
定义1 由上述半范数族S={Pλ,λ>ω}所确定的X上的局部凸向量拓扑称为 C-余弦算子函数拓扑,相应的局部凸线性拓扑空间记为(X,τ)。
引理 1[3]设 E是线性空间,A,B是 E上的两族半范数,则由 A确定的拓扑弱于由B确定的拓扑的充要条件是:对于每个 q∈A,必存在 p1,p2...pm∈B以及正数 c1,c2...cm使得对一切 x∈E成立:
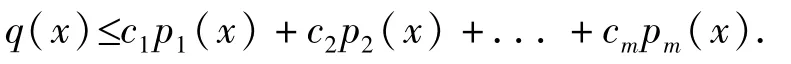
定理1 X上的 C-余弦算子函数拓扑弱于由范数所确定的局部凸向量拓扑。
证明 由于对任意 λ>ω及 x,y∈X有:

由此及引理1,易见定理成立。
定义2 在一局部凸线性拓扑空间X中,若对任意的Cauchy序列{xn},{R(λ2,A)xn}(λ>ω)都收敛,则称 X是 C-余弦算子函数完备的。
定理2 局部凸线性拓扑空间(X,τ)是C-余弦算子函数完备的。
证明 设{xn}是(X,τ)中的任意 Cauchy序列,则对于任意连续半范数q(x)及ε>0,集合U={x:q(x)<ε}构成0的一个邻域,从而必存在自然数N,使得当n,m>N时,有(xn-xm)∈U,即q(xn-xm)<ε,特别地,对任意pλ(x)∈S有
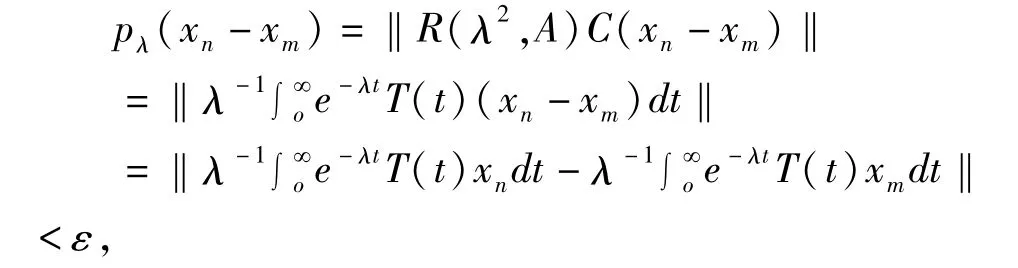
可知{R(λ2,A)Cxn}(λ>ω)是 Banach空间(X,‖●‖)中的 Cauchy序列,从而{R(λ2,A)Cxn}(λ>ω)必收敛,再由定理1知{R(λ2,A)Cxn}(λ>ω)也是(X,τ)中的收敛列。
由于pλ(x)=‖R(λ2,A)Cx‖≤‖R(λ2,A)C‖·‖x‖,所以拓扑τ弱于由范数所确定的一局部凸向量拓扑,从而当{T(t),t∈R}是(X,‖●‖)上的C-余弦算子函数时,它也是局部凸线性拓扑空间(X,τ)上的C-余弦算子函数。
对于由单个半范数诱导的局部凸向量拓扑,有如下结果:
定理3 设 λ,μ>ω且 λ2,μ2∈ρ(A),则由半范数 pλ(x)=‖R(λ2,A)Cx‖所确定的局部凸向量拓扑与由半范数 pμ(x)=‖R(μ2,A)Cx‖所确定的局部凸向量拓扑等价。
证明 因为由预解方程知,对任意 λ2,μ2∈ρ(A)有

则对任意 x∈X有:
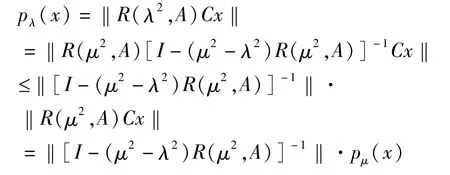
类似地,有
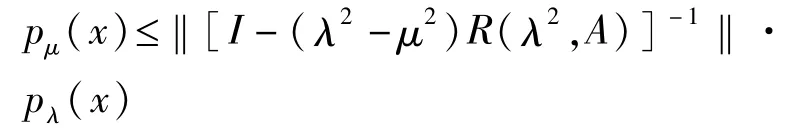
再利用引理1,即可得本定理成立。
[1]赵华新.C-半群拓扑[J].河南科学,2006(2):169-171.
[2]王晓梦,赵华新,常胜伟.积分 C-半群拓扑[J].延安大学学报,2008(2):5-6.
[3]夏道行,杨亚力.线性拓扑空间引论[M].上海:上海科学技术出版社,1986.
[4]郑权,雷岩松.指数有界的C-余弦算子函数[J].系统科学与数学,1996(3):242-252.
[责任编辑 贺小林]
C-cosine Operator Function Topological
BIWEI,ZHAO Hua-xin
(College of Mathematics and Computer Science,Yan an University,Yan an 716000,China)
By using the C-cosine operator function,a new locally convex vector topologicalwas introducted,and propositions of itwere given.
cosine operator function;locally convex vector topological;generator;C-cosine operator function topological
O177.3
A
1004-602X(2011)02-0013-02
2011 -03 -22
毕伟(1986—),男,陕西米脂人,延安大学在读硕士研究生。

