一类双复合风险模型的破产概率的初步研究

乔克林，李 萍，侯致武

（延安大学 数学与计算机科学学院，陕西 延安 716000）

一类双复合风险模型的破产概率的初步研究

乔克林，李 萍，侯致武

（延安大学 数学与计算机科学学院，陕西 延安 716000）

考虑对保单到达过程进行 P－稀疏来描述理赔到达的双复合 Poisson过程，并用比例再保险的方式降低保险公司的风险，加入不确定因素对建立的模型进行随机干扰，得到了该模型破产概率的一般表达式及破产概率的一个上界估计，通过构造鞅的方法，得到了模型的 Lundberg方程，并证明了调节系数的存在性。

稀疏过程；再保险；破产概率；双复合风险模型；干扰项；

在经典风险模型的假设条件中，保费到达过程与理赔到达过程是相互独立的，实际问题中，随着人们保险意识及市场竞争不断的发展，保险公司受到了来自社会、经济、军事等各方面的影响，其经营的风险模型也越来越复杂，对于相互独立条件的改进，我们考虑保费到达过程与理赔到达过程之间的数字特征的相互关联性，如期望的相依性、比例关系更符合市场的实际情况。文献［1］中，采用 Poisson过程来描述保单到达过程，是对经典风险模型的一种更加实用性的改进，但是它仍考虑保费与理赔的相互独立性，未考虑到保费与理赔之间数字特征的相关性对保险公司实际运营的影响。文献［2－4］考虑了理赔到达过程是保费到达过程的 P－稀疏过程，对经典风险模型的一大发展，但未考虑再保险因素对保险公司生存概率的影响。文献［5］仅考虑了再保险对保险公司的影响，所建立的模型中保费收取是简单的线性增长，简化了实际中的保费收取过程，在实际应用中有一定的局限性。本文是在以上文献的基础上，考虑保费到达过程和理赔到达过程均为复合 Poisson过程，且理赔到达过程是对保费到达过程进行随机 P－稀疏来描述的，同时考虑再保险因素对风险模型生存概率的影响，并且在模型中加入随机干扰项，以此体现实际中保险公司受到的除保费与理赔之外的其它不确定因素的影响。使建立的风险模型更加具有实际意义，本文对该模型的破产概率及上界估计等一些初步的风险精算指标进行了研究。

1 模型建立

定义1.1 设（Ω，F，P）是一个完备的概率空间，本文中的所有随机变量都定义在这一空间上，对u≥0，t≥0，定义保险公司在 t时刻的盈余为

其中，u是保险公司初始资金；q（0＜q＜1）为保险公司的比例再保险水平，则再保险公司赔付的理赔额为X（1－P）；｛N（t），t≥0｝为保单到达过程，即保险公司在时间［0，t］内到达的保单数；｛Np（t），t≥0｝为理赔到达过程，即保险公司在时间［0，t］内的总理赔次数；Xk为第 k次的理赔额，Yk为第 k张保单的保费收入。｛W（t），t≥0｝是标准布朗运动，表示保险公司除保费和理赔之外的不确定收入和支出。

我们对上述模型假设如下：

（1）｛Xk，k≥1｝，｛Yk，k≥1｝是取值于［0，∞）上的非负独立同分布的随机变量序列，其分布函数分别是F（x），G（y）。均值分别为 μx，μy。方差分别为

（2）｛N（t），t≥0｝是参数为λ的 Poisson过程，理赔到达过程｛Np（t），t≥0｝是保单到达过程｛N（t），t≥0｝的p－稀疏过程，即｛Np（t），t≥0｝是参数为 λp（0＜p＜1）的 Poisson过程。

（3）｛Xk，k≥1｝，｛Yk，k≥1｝，｛N（t），t≥0｝，｛Np（t），t≥0｝，及｛W（t），t≥0｝相互独立。

为了确保保险公司能够稳定经营，需要假设 E［S（t）］＞0，即

此外，易证盈利过程｛S（t），t≥0｝是一平稳独立增量过程。

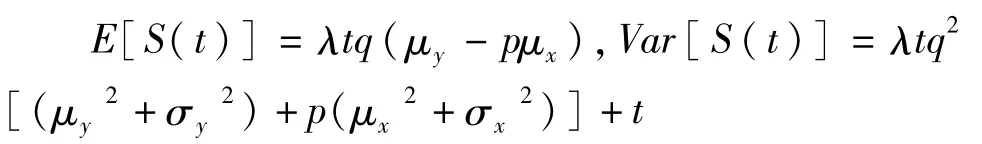
定义1.2 保险公司盈余首次为负值时刻，定义为破产时刻，记为 T，则

T＝inf｛t≥0，U（t）＜0，U（0）＝u｝.对 T＝∞时，则对∀t＞0，有 U（t）＞0，即保险公司不会发生破产，定义最 终破产 概率 为 ψ（u）＝pro｛T＜∞，则生存概率为 Φ（u）＝1－ψ（u）.定义保险公司在时间 t之前发生破产的概率为 ψ（u，t），在时间t之前的生存概率为Φ（u，t）＝1－ψ（u，t）。

记保费额随机变量 Yk的 Laplace变换为

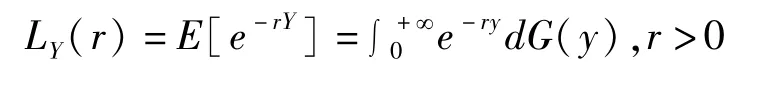
记理赔额随机变量 Xk的矩母函数为

假设 LY（r）＜∞，并存在 r*＞0（r*可以为∞），使得当 r→r*时，有 MX（r）→∞，即∃r*使得

定义1.3 对于盈利过程｛S（t），t≥0｝，定义事件流Fs＝｛，t≥0｝，其中

2 几个引理

引理2.1 对于盈利过程｛S（t），t≥0｝，存在函数 g（r），使得 E［e－rS（t）］＝etg（r）

证明

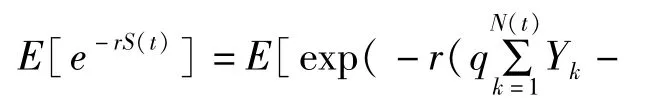
MX（r）为保费的矩母函数，LY（r）为理赔的 Laplace变换，令

即 有 E［e－rS（t）］＝etg（r）。证 毕 。

引理2.2 方程g（r）＝0在其定义域内有唯一正解R，称R为调节系数。

所以 g′（0）＝－λq（μy－pμx）＜0，又因为

所以 g（r）在（0，r*）内是凸函数，故方程g（r）＝0在（0，r*）内至多有两个解，r＝0是平凡解，又因为当 r→r*时有 g（r）→∞，所以方程g（r）＝0在其定义域内有且只有一个正解，记为 R，称其为调节系数。证毕。

证明 对∀v≤t，由引理2.1知

所以｛Mu（t），t≥0｝是 FS下的鞅。证毕。

3 破产概率

定理3.1 风险模型的最终破产概率满足 Lundberg不等式

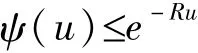
证明 因为 T是 Fs停时，选 t0＞0，则T∧t0是Fs的停时，由引理 2.3得

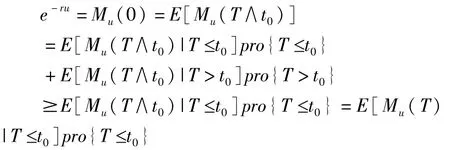
因为当T＜∞时，有 u＋S（T）≤0，所以 e－r（u＋S（T））≥1，所以由

令 t0→∞，有，取｛r：g（r）≤0｝，证毕。

定理3.2 对任意的 u≥0，r＞0有

其中 R为调节系数。

证明 因为 T是 Fs的停时，对∀t0＜∞。由有界停时定理知，T∧t0是 Fs停时。∀u≥0，r＞0有

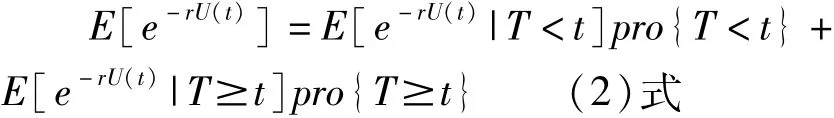
（2）式右端第一项记为 I1，第二项记为I2。由于

故（2）式左端 E［e－rU（t）］＝E［exp｛－

选 r＝R，则上式可化简为 E［e－rU（t）］＝e－Ru。在I1中，U（t）可以写成

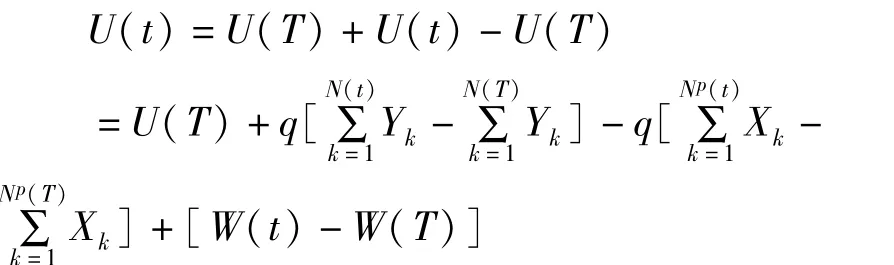
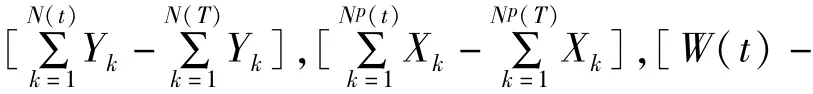
给定 t，当 T＜t时 W（T）］和U（T）是相互独立的，且是服从参数为 λ（t－T）的复合泊松过程，是服从参数为 λp（t－T）的复合泊松过程，是的稀疏过程。所以

选 r＝R，则有 I1＝E［e－RU（T）｜T＜t］pro｛T＜t｝

于是 （2）式化简为

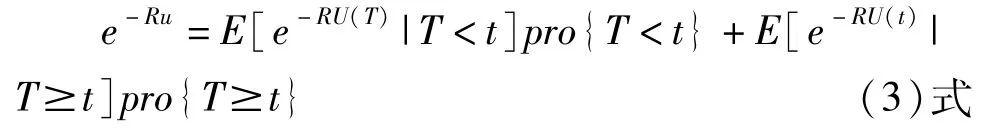
令 t→∞，（3）式右端第一项为 E［e－RU（T）｜T＜∞］ψ（u）。下面证明（3）式右端第二项当 t→∞时趋于0。

因为E［U（t）］＝E［u＋S（t）］＝u＋E［S（t）］＝u＋λtq（μy－pμx）

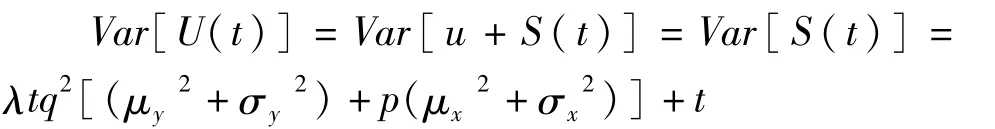
令 α＝λq（μy－pμx）＞0，β2＝λq2［（μy2＋σy

2）＋p（μx2＋σx2）］＋1。

q（t）＝u＋αt－βt2／3，因 α＞0，在t充分大的时候，q（t）＞0。因此

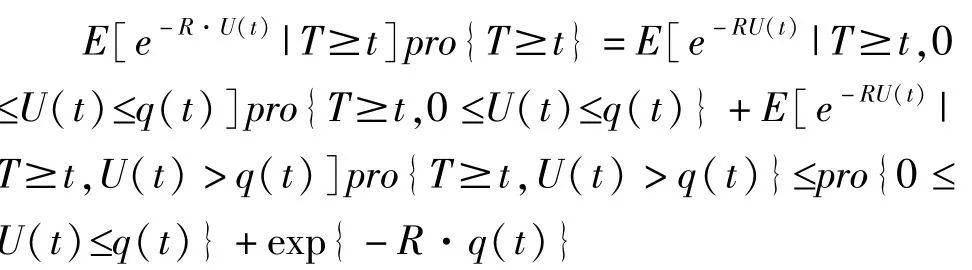
由契比雪夫不等式：

故当 t→∞时，0≤E［e－RU（t）｜T≥t］≤t－1／3＋e－Rq（t）→0.

综上所述，有 e－RU（t）＝ψ（u）E［e－RU（T）｜T＜∞］.则得定理结论。

由此定理可推得定理 3.1成立.因为当 T＜∞时，U（T）＜0，因此 E［e－RU（t）｜T＜∞］＞1，则由以上定理有 ψ（u）＜e－Ru。

［1］龚日朝，李季风.双 Poisson风险模型下的破产概率［J］.湘潭师范学院学报（自然科学版），2001，23（1）：55－57.

［2］李俊海.具有相关性的 Poisson分布风险模型［J］.郑州工业高等专科学校学报，2004，20（4）：1－3.

［3］夏亚峰，顾群.带投资和干扰项的相依风险模型［J］.甘肃科学学报，2010，22（1）：122－125.

［4］赵金娥，王贵红，龙遥，等.索赔为稀疏过程的双复合Poisson风险模型［J］.经济数学，2010，27（4）：86－92.

［5］成军祥，王变.带干扰的再保险风险模型的破产概率［J］.北京电子科技学院学报，2010，18（2）：1－3.

［6］成世学.破产论研究综述［J］.数学进展，2002，31（5）：403－422.

［责任编辑 贺小林］

The Prelim inary Research of Ruin Probabilities for a Class of Double Compound Risk M odel

QIAO Ke－Lin，LIPING，HOU Zhi－Wu
（College of Mathematics，Yan an University shannxi716000，China）

A riskmodelwith double compound poisson processwas studied，in which the arrival of the claims is a p－thining process of the arrival of the premium incomes.and reduced the risk of the insurance company with the proportional re－insurance.Meanwhile，the effect of the random interference on the ruin probability of insurance company were analyzed.The general expression of the ruin probability and an uper bound of the ruin probability were given.Lundberg equation of the ruin probability is provided bymeans ofmartingalemethod，and the existence of adjustment coefficientwas proved.

thinning process；re－insurance；ruin probability；double compound risk model；interference

O211.67

A

1004-602X（2011）02-0027-04

2011 -03 -28

陕西省教育厅自然科学基金（2010JK914）；延安大学教改项目（YDJG10－02）

乔克林（1964—），男，陕西佳县人，延安大学副教授，硕士。