一个包含平方补数的复合函数

穆秀梅，郭金保，何桃，赵杏花

（延安大学 数学与计算机科学学院，陕西 延安 716000）

一个包含平方补数的复合函数

穆秀梅，郭金保，何桃，赵杏花

（延安大学 数学与计算机科学学院，陕西 延安 716000）

利用初等和解析的方法研究复合函数 SL( SSC( n ))的均值，并得到了一个有趣的渐进公式。

平方补数；Smarandache LCM函数；复合函数；均值；渐进公式

对于任意的正整数n，著名的 F.Smarandache LCM函数 SL (n)定义为最小的正整数 k使得 n｜[1 ，2，…，k]，其中 [ 1，2，…，k]表示1，2，…，k的最小公倍数，即

从 ()SL n的定义和性质，很容易推断，对于任意

关于 ()SL n的初等性质，许多学者进行了研究，获得了一系列有趣的结果。例如文献［1］中，证明了对任意给定的正整数 k及任意实数 x＞2有渐进公式，则有

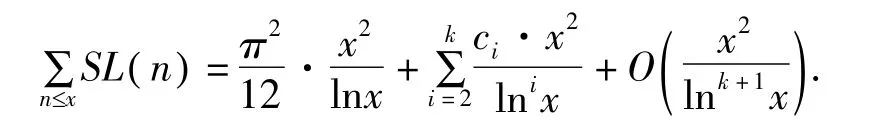
其中 ci( i＝1，2，…，k)是可计算的常数。设 n为任一正整数， ()SSC n表示使 mn为一完全平方数的最小正整数 m，即

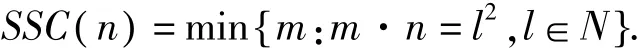
在文献［2］中，F.Smarandache教授要求我们研究数列 {SSC (n )｝的性质.对此已有许多学者进行了研究，取得了一系列研究成果。例如文献［3］中，刘红艳、苟素用初等方法研究了 SSC (n)和的均值，文献［4］中，张文鹏教授和徐哲峰博士研究了Smarandache函数作用于平方补数上的均值公式，得到了较强的渐进公式，即

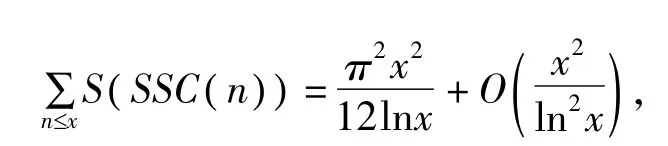
这里用 ()S n表示 Smarandache函数，即 ()S n ＝min{ m：n m！，m∈N｝.

定理 对任一实数 x≥3，有渐进公式

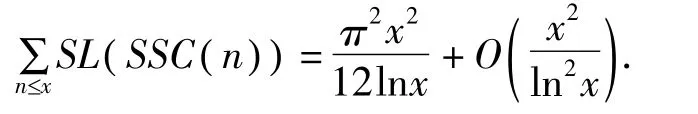
为了完成定理的证明，我们需要引入一些引理，为简单起见，用 ()p n表示 n的最大素因子。

证明：（1）当 n是一个无平方因子数，有 n＝p1p2…pr( )p n，则

即

上面为引理1的证明。

引理 2 当 p为一素数时，有渐进公式

成立。

证明：令 π()x表示不大于x的素数的个数，我们有

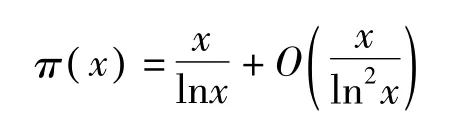
成立。由 Abel恒等式，可得出

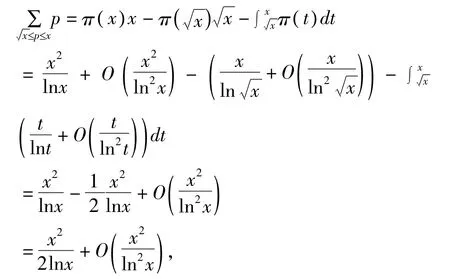
即引理2得证。

定理的证明 由以上的引理，我们有

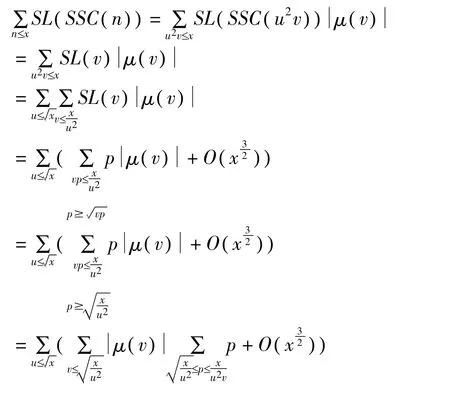
从而完成了定理的证明。

［1］Lv Zhongtian.On the F.Smarandache LCM function and its mean value［J］.Scientia Magna，2007，3（1）：22－25.

［2］Smarandache F.Only problems，not solutions［M］.Chicago：Xiquan Pulishing House，1993.

［3］刘红艳，苟素.关于F.Smarandache的一个问题［J］.延安大学学报，2001，2（3）：5－6.

［4］ZhangWenpeng and Xu Zhefeng.On the Smarandache function and square complements［J］.Scientia Magna，2005（2）：1－4.

［5］Apostol T M，Introduction to analytic number theory［M］. New York：Spring－Verlag，1976.

［责任编辑 贺小林］

A Com posite Function Involving the Square Com p lements

MU Xiu－mei，GUO Jin－bao，HE TAO，ZHAO Xing－hua
（College of Mathematics and Computer Science，Yan an University，Yan an 716000，China）

Themain purpose of this paper is using the elementary and analytic methods to study the mean value properties of the composite functionSL (SSC( n ))，and giving an interesting asymptotic formula.

square complements；Smarandache LCM function；composite function；mean value；asymptotic formula

O156.4

A

1004-602X（2011）02-0007-02

2011 -03 -28

穆秀梅（1988—），女，陕西铜川人，延安大学在读硕士研究生。