偏序半群的理想的根、偏序同态和商序同态

邵海琴，郭莉琴，何建伟，王力梅

（天水师范学院 数学与统计学院，甘肃 天水741006）

偏序半群的理想的根、偏序同态和商序同态

邵海琴，郭莉琴，何建伟，王力梅

（天水师范学院 数学与统计学院，甘肃 天水741006）

通过偏序半群的理想的根，刻画了偏序半群的偏序同态与商序同态的一些重要性质，并得到了一些重要结论。

偏序半群；理想；理想的根；偏序同态；商序同态

偏序同态和商序同态是偏序半群中一个重要的研究课题，许多学者都对其进行了深入细致的研究。而偏序半群的一些重要概念在偏序半群各类问题特别是与偏序同态和商序同构有关的问题的研究中起着举足轻重的作用［1－4］。文献［1］通过拟序，主要讨论了偏序半群的拟序和同态之间的关系；文献［2］通过商拟序，给出了商序同态基本定理，并得到了商拟序和商序同态的一些重要性质；文献［3］利用半拟序，给出了偏序半群的偏序扩张与有限全序扩张的方法；文献［4］利用自然序半格拟序，研究了偏序半群的真滤子并构造了最小自然序半格拟序。本文通过偏序半群的理想的根，刻画了偏序半群的偏序同态与商序同态的一些重要性质，并得到了一些重要结论。

1 预备知识

定义 1［5］如果（S，·）是半群[]6，（S，≤）是偏序集且偏序对乘法运算是相容的，即

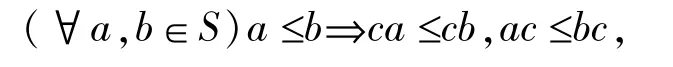
则称（S，·，≤）是偏序半群。

定义2［5］设（S，·，≤）是偏序半群，φ≠L⊆S若L满足

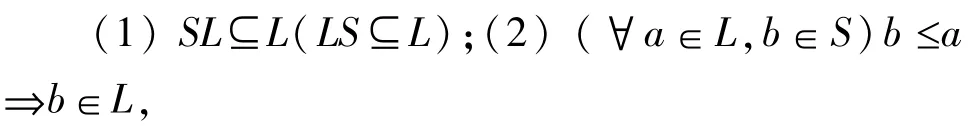
则称L是S的左（右）理想。若L既是S的左理想又是 S的右理想，则称 L为 S的理想。

定义 3［5］设（S，·，≤）是可换偏序半群，I是 S的理想。那么集合称为 I的根，记为

定义4［5］设（S，·，≤S），（T，*，≤T）是偏序半群。映射 φ称为 S到T的同态映射，如果 φ满足

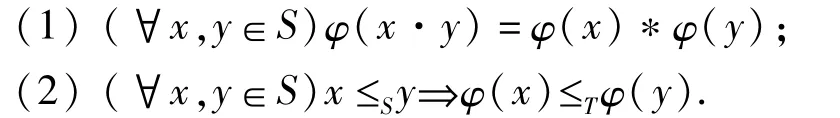
若 φ为 S到 T的同态映射，且 φ是满（单）的，则称φ为 S到T的满（单）同态。

定义5［2］设（S，·，≤S），（T，*，≤T）是偏序半群。S到T的同态映射 φ称为商序同态，如果φ满足

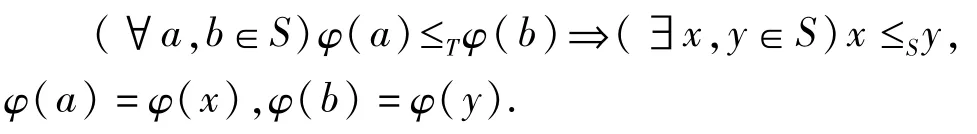
设（S，·，≤S），（T，*，≤T）是偏序半群，φ是S到T的商序同态。若φ是满（单）的，则称φ是 S到 T的商序满（单）射；若φ是双射，则称 φ是S到T的商序同构。

2 主要结果

命题1 设（S，·，≤S），（T，*，≤T）是偏序半群，I是 S的理想，φ是S到 T的商序满同态。令φ，那么φ（I）是T的理想。

证明 显然，φ≠φ（I）⊆T。下面证明φ（I）是T的理想。

（i）对任意的a∈φ（I），b∈T，由 φ是满的和 φ（I）的定义得

对y∈S，x∈I，因为I是S的理想，所以xy∈I且yx∈I，于是由 φ（I）的定义和 φ是 S到T的同态得

即 φ（I）T⊆φ（I）且Tφ（I）⊆φ（I）.

（ii）对任意的 b∈T，a∈φ（I），由 φ（I）的定义和 φ是满的得

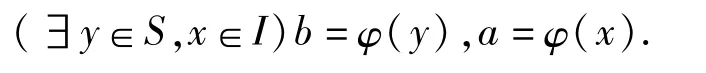
若 b≤Ta，即 φ（y）≤Tφ（x），则由 φ是S到 T的商序同态得

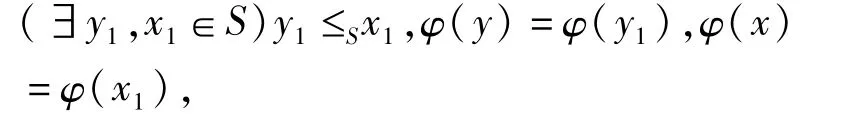
于是对 a＝φ（x）＝φ（x1）∈φ（I），由 φ（I）的定义得x1∈I，因为 I是S的理想，所以 y1∈I，从而由φ（I）的定义得 φ（y1）∈φ（I），即b∈φ（I）.

综上所述，φ（I）是 T的理想。

定理1 设（S，·，≤S），（T，*，≤T）是偏序半群，I是 S的理想，为I的根，φ是 S到T的商序满同态。令

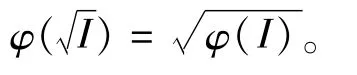
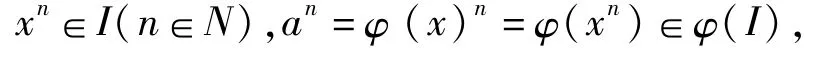
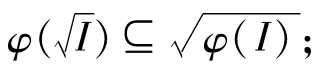
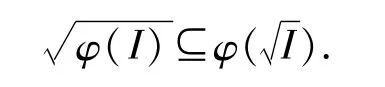
命题2 设（S，·，≤S），（T，*，≤T）是偏序半群，I是 T的理想，φ是 S到 T的偏序满同态.令，那么 φ－1（I）是 S的理想。

证明 显然，φ≠φ－1（I）⊆S。

（i）对任意的x∈φ－1（I），y∈S，由 φ－1（I）的定义和 I是 T的理想得

φ（x）φ（y）∈I且 φ（y）φ（x）∈I，于是由 φ是 S到 T的同态得 φ（xy）∈I且 φ（yx）∈I。因此由 φ－1（I）的定义得 xy∈φ－1（I）且yx∈φ－1（I），即

（ii）对任意的x∈φ－1（I），y∈S，由 φ是 S到 T的同态和 φ－1（I）的定义得

φ（x）∈I，φ（y）∈T。若y≤Sx，则由 φ是保序的得φ（y）≤Tφ（x）.因为 I是 T的理想，

所以 φ（y）∈I.从而由φ－1（I）的定义得

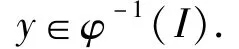
综上所述，φ－1（I）是 S的理想。

定理2 设（S，·，≤S），（T，*，≤T）是偏序半群，I是 T的理想，为 I的根，φ是S到 T的偏序满同态。令

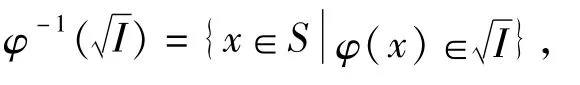
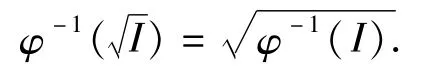
证明 由命题2知 φ－1（I）是S的理想。下面证明为 φ－1（I）的根，即

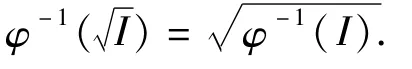
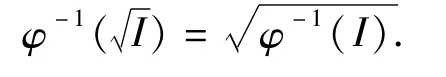
命题3 设（S，·，≤S），（T，*，≤T）是偏序半群，I是S的理想，φ是S到T的商序满同态。那么

（1）φ－1（φ（I））是S的理想且φ－1（φ（I））＝I；

证明 （1）由命题 1和命题 2可得 φ－1（φ（I））是 S的理想。下面证明 φ－1（φ（I））＝I。

一方面，对任意的 x∈φ－1（φ（I）），由 φ－1（φ（I））的定义可得 φ（x）∈φ（I），于是由φ（I）的定义得x∈I，即φ－1（φ（I））⊆I；另一方面，对任意的x∈I，由 φ（I）的定义得 φ（x）∈φ（I），又由 φ－1（φ（I））的定义可得 x∈φ－1（φ（I）），即 I⊆φ－1（φ（I））。

综上所述，φ－1（φ（I））＝I.

命题4 设（S，·，≤S），（T，*，≤T）是偏序半群，I是T的理想，φ是S到T的商序满同态。那么

（1）φ（φ－1（I））＝I；

证明 （1） 由命题 1和命题 2可得φ（φ－1（I））是T的理想。下面证明 φ（φ－1（I））＝I.

一方面，对任意的 a∈φ（φ－1（I）），由 φ（φ－1

a＝φ（x）。对 x∈φ－1（I），由φ－1（I）的定义得φ（x）∈I，即a∈I，因此φ（φ－1（I））⊆I；另一方面，对任意的 a∈I，由 φ是满的和φ－1（I）的定义得存在 x∈φ－1（I）使得

a＝φ（x）。又对 x∈φ－1（I），由 φ（φ－1（I））的定义可得 φ（x）∈φ（φ－1（I）），即

a∈φ（φ－1（I））。因此I⊆φ（φ－1（I））.

综上所述，φ（φ－1（I））＝I；

（2） 由（1）、定理1和定理 2可得φ（φ－1所以

［1］Kehayopulu N，Tsinglis N.Pseudoorder in ordered semigroups［J］.Semigroups Forum，1995（50）：389－392.

［2］Cao Y L.Quotient ordered homomorphisms of ordered Semigroups［J］.Communications in Algebra，2003（31）：5563－5579.

［3］邵海琴，薛占军，雷振亚.偏序半群的偏序扩张［J］.纯粹数学与应用数学，2008，24（4）：1－6.

［4］Cao Y L.Decompositions and pseudo－orders of ordered semigroups［J］.Semigroups Forum，2004（68）：177－185.

［5］谢祥云.序半群引论［M］.北京：科学出版社，2001：1－7.

［6］Howie JM.An introduction to semigroups theory［M］. London：Acad.Press，1976.

［责任编辑 贺小林］

Radical of an Ideal，Partially Ordered Homomorphism s and Quotient Ordered Homomorphism s of Partially Ordered Sem igroups

SHAO Hai－qin，GUO Li－qin，HE Jian－wei，WANG Li－mei
（School of Mathematics and Statistics Institute，Tianshui Normal University，Tianshui741001，China）

Some important properties on partially ordered homomorphism and quotient ordered homomorphism of partially ordered semigroupswere depicted by radical of an ideal of partially ordered semigroups，and some important conclusions were obtained.

partially ordered semigroups；ideal；radical of an ideal；partially ordered homomorphisms；quotient ordered homomorphisms

O152.7（2000MR）20M25

A

1004-602X（2011）02-0004-03

2011 -03 -19

邵海琴（1971—）女，甘肃天水人，天水师范学院副教授，硕士。