安装在曲面平台上的共形阵快速计算方法研究

何庆强

(中国西南电子技术研究所，四川 成都 610036)

共形阵是天线单元附着在非平面表面上的天线阵，它不仅具有良好的空气动力学特性，而且可以节省载体空间和实现宽角扫描，降低雷达散射截面积(RCS)和减小天线与天线罩之间的相互影响.因此最近几年来共形阵的分析与综合受到国内外广泛关注，典型的分析方法有矩量法[1]、有限元法[2]、以及时域有限差分技术[3-4].但是这些数值技术对于分析实际的共形阵问题通常要求极大的计算域，同时归于计算机硬件条件的限制，数值技术很难分析安装在曲面载体上的共形阵问题.另一方面，基于曲面平台载体曲率的影响，共形阵新的远场行为将出现，导致经典的线阵或面阵分析方法失效.因此，对于共形阵的分析与综合，国际上提出了一些新的技术[5-7]，但是这些技术忽略了单元互耦对阵列辐射特征的影响，而且安装平台对阵列辐射特征的影响也没有严格地考虑.

本文提出一个新的共形阵快速计算方法.通过划分阵列单元为不同的部分，同时忽略更远单元的弱互耦影响，一个复杂的共形阵问题被分成各类简单的子阵问题的叠加，极大地降低了计算负担.坐标转换理论被用来创建极化分量，一个通用的单元极化分量计算被执行.数值结果描述了共形阵的行为特性，验证了该新方法的有效性.所有的计算结果表明：对于大型共形阵的计算，当其他数值计算由于受计算机硬件条件的限制而无法实现时，采用有源单元方向图技术是非常有效的.

图1 典型的曲面阵几何结构

1 新方法的提出

典型的曲面共形阵几何结构显示在图1中，应用远场叠加原理，曲面共形阵的远场可以表示为：

(1)

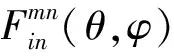
对于曲面共形阵，当第mn单元被激励而其他所有单元被匹配时，所获得的单元方向图是包含单元互耦和载体平台影响的有源单元方向图.对于一个大型阵列，有源单元方向图正比于增益方向图.对于无限阵，有源单元方向图可以表示为[8]：

事实上，当共形阵拥有几十个或数百个辐射单元时，这对共形阵的分析提出了极大的挑战：单元激励和相位调制方法不再实用，因为有源单元方向图要求提取每个单元的数据.一个有效的方法是将阵列分成不同的部分，即边缘单元、中间单元、以及邻边单元.通常，边缘单元考虑成共形阵最边上的行或列；而邻边单元则介于边缘单元和中间单元之间.对于一个具体的激励单元，即有源单元，只需在阵列中提取一次，这样极大地降低了计算负担.因此对于共形阵的远场方向图计算，式(1)可以重新写为：

(2)

(3)

式中:R(βmn,αmn,γmn) 是一个3×3的欧拉旋转矩阵[10-11]，并且有:

X=sinθcosφ;Y=sinθsinφ;Z=cosθ

(4)

(5)

2 数值结果和探讨

为了验证提出的方法的正确性，一个8×8曲面共形阵被研究.如图2所示，曲面半径Rc选择为6λ0，其中λ0是天线工作在23GHz时的自由空间波长.每个辐射单元被均匀地排列，其单元间距在x-向为Dx=6.8mm，在θ-向为Δθ=50.

图2 曲面共形阵和它的辐射单元

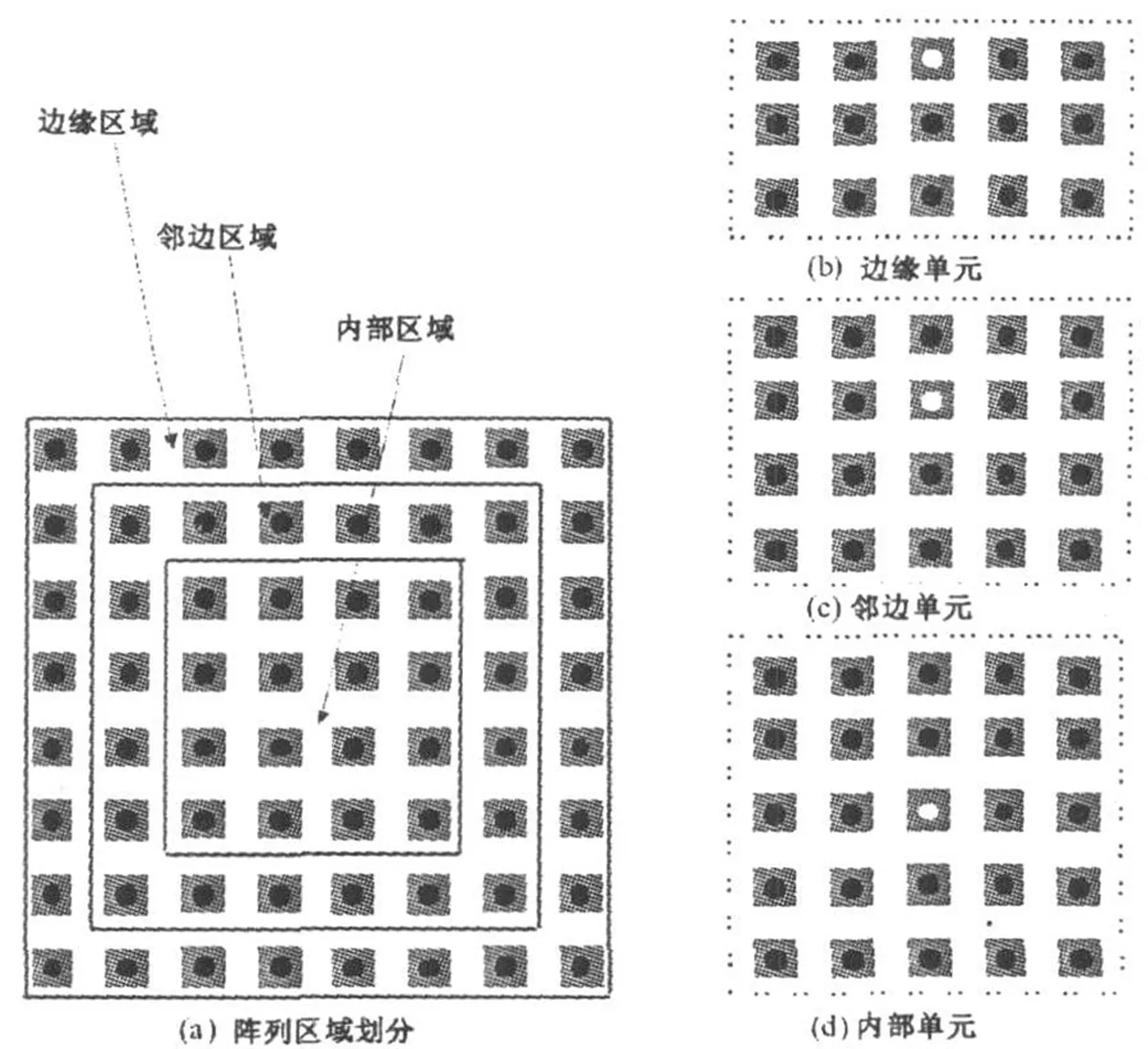
图3 提出的子阵提取技术和激励单元

这里，辐射单元选择为一个半径为R的圆形贴片，它印刷在介质厚度为h2相对介电常数为εr2的介质板上.在该介质层的上面，一层厚度为h1相对介电常数为εr1的介质来加载这个辐射单元，以降低天线尺寸.耦合十字槽的臂长分别为ls1和ls2，宽度为ws，它印刷在介质厚度为h3相对介电常数为εr3的介质上.宽度为wa的悬置微带作为RF信号传输线，在这RF信号传输线的左端，一个 50Ω 同轴探针(SMA) 被用来激励这辐射单元.在这RF信号线的右端，设计了一个长度为la的匹配调谐传输线，它印刷在介质厚度为h4相对介电常数为εr4的介质板上.辐射单元的地面尺寸是0.5λ0×0.5λ0，整个结构如图2所示.

如图3所示，这多层微带共形阵能够被分成边缘区域、中间区域和邻边区域.在图3(b)、(c)和(d)中的白点代表了该单元被激励，黑点表示该单元被匹配.对于具体的激励单元，即有源单元，互耦主要来自临近的单元，更远单元的互耦可以被忽略[11]，因此这有源单元能够被计算基于子阵提取的方式，从而极大地减少了计算负担.这里：边缘单元可以在一个3×5的子阵中提取，邻边单元可以在一个4×5的子阵中提取，中间单元可以在一个5×5的子阵中提取.

明显地，基于载体曲率的影响，共形阵的互耦通常在x-向和θ-向是不同的.因此曲率对互耦的影响应该首先研究.通过仿真分析，可以看出：互耦受曲率的影响在这个例子里可以被忽略.因此在提取有源单元方向图时可以选择在x-向或θ-向，从而再一次地减少了计算负担.

图4显示了理想单元方向图和有源单元方向图，它清晰地显示出由于互耦和载体的影响，有源单元方向图不同于孤立单元方向图.通过上面的分析，一个8×8的多层曲面共形阵列被设计.图5画出了这8×8阵列的远场方向图.从图5可以看出，使用有源单元方向图技术和全波软件HFSS仿真所得的结果是一致的，从而有效地验证了方法的正确性.

图4 计算的有源单元方向图和孤立单元方向图

图5 一个8×8多层微带共形阵列远场方向图

表1 给出了采用有源单元方向图技术和采用全波软件HFSS仿真所要的计算时间.显然新方法具有更高的效率.通过进一步计算发现，由于受计算机硬件条件的限制，当阵列单元超过64元时全波软件HFSS软件已无能为力.在这个例子里，所有的仿真在一个Intel Pentium IV 3.3-GHz和32-G RAM的计算机上进行.

表1 提出的方法与全波仿真计算的时间比较

3 结论

对于共形阵，通常矢量单元方向图不能从共形阵的远场中分离出来，因此共形阵的计算是非常复杂的.此外，互耦和装配平台对共形阵的影响也必须严格地考虑.本文研究了多层共形阵列的互耦和曲率的影响，通过划分所有单元为不同的部分并忽略弱互耦影响，一个大型阵列计算问题被分成了各类简单的子阵问题的叠加，极大地减少了计算负担.数值结果验证了提出的方法的正确性.

参考文献:

[1]Thors B， Josefsson L. Radiation and scattering tradeoff design for conformal arrays[J].IEEE Trans Antenna Propagat, 2003，51(5)：1069-1076.

[2]Paul D L， Craddock I J， Railton C J.Simulation of circular conformal facetted stacked patch antenna array with tight radius of curvature by hybrid Cartesian/cylindrical FDTD approach[C]// Proceedings of Third European Workshop on Conformal Antennas, Bonn, Germany,2003,22/23:53-56.

[3]Macon C A, Kemple L C, Schneider S W.Modeling cavity-backed apertures conformal to prolate spheroids using the Finite element-boundary integral technique[C]//Proceedings of IEEE AP-S international symposium, 2002:550-553.

[4]Allard R J, Werner D H, Werner P L. Radiation pattern synthesis for arrays of conformal antennas mounted on arbitrarily-shaped three-dimensional platforms using genetic algorithms[J] IEEE Trans Antenna Propagat, 2003,51(5):1054-1062.

[5]Sun J S, Goshi D S, Itoh T.Optimization and modeling of sparse conformal retrodirective array[J].IEEE Trans Antenna Propagat, 2010, 58(3): 977-981.

[6]Li W T, Shi X W,. Hei Y Q, et al. A hybrid optimization algorithm and its application for conformal array pattern synthesis[J]. IEEE Trans Antenna Propagat., 2010, 58(10): 3401-3406.

[7]Ouyang J, Yang F, Guan L,et al.Enhancing the convergence speed of space mapping technique in cylinder conformal antennas optimization[J]. J of Infrared, Millimeter and Terahertz Waves, 2010,31(2):162-168.

[8]KelleyD F, Stuzman W L. Array antenna pattern modeling methods that include mutual coupling effects[J]. IEEE Trans Antenna Propagat, 1993, 42(2):1625-1632.

[9]He Q Q, Wang B Z, Shao W.Radiation pattern calculation for arbitrary conformal arrays that include mutual coupling effects[J].Antenna Propagat Mag, 2010, 52(2):57-63.

[10]Milligan T. More Applications of Euler Rotation Angles[J]. IEEE Antenna Propagat Mag,1999, 41(4):78-83.

[11]Rao P M,Raju G S N.Studies on mutual coupling between radiating elements[C]// Proceedings of the 9th Int Conf,INCEMIC, Electromagnetic Interference and Compatibility, 2006:549-551.