曲面离散载荷在仿真分析中的施加方法

徐新栋, 李建辰, 曹小娟, 龚 平



曲面离散载荷在仿真分析中的施加方法

徐新栋1,2, 李建辰1,2, 曹小娟1, 龚 平3

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710075; 2. 水下信息与控制重点实验室, 陕西 西安, 710075; 3. Abaqus北京代表处, 北京, 100025)

针对有限元仿真分析中曲面上大量离散分布载荷施加困难的问题，提出了基于曲线拟合和线性插值的曲面分区拟合法，应用于由单调曲线回转而成的轴对称曲面上，求出载荷值沿各曲面分区的函数表达式，并通过表达式进行快速有效加载，提高了有限元前处理的效率。在模型风洞试验仿真分析中对该方法进行了应用验证，结果表明, 该方法简单有效且能保证较高的精度。

有限元方法; 离散分布载荷; 曲面分区拟合法; 仿真

0 引言

有限元仿真分析是武器装备研发的重要方法之一, 对提高产品设计水平、降低试验成本、缩短研发周期有着重要的意义。其过程一般分为前处理、求解、后处理3个阶段。随着计算机技术的发展和商用有限元软件的不断更新, 求解器和后处理发展日趋完善, 分析工程师的主要精力用在建模、划分网格、设置边界条件、施加载荷等前处理上。其中, 在曲面上施加不均匀分布载荷往往比较困难, 会耗费大量时间精力, 严重影响了前处理的效率。对此, 文献[1]提出了基于特征函数分布的曲面有限元不均匀分布载荷施加方法, 解决了已知载荷分布函数情况下不规则曲面载荷的施加问题。然而工程中载荷分布函数往往是未知的, 如在进行火箭助飞鱼雷头帽曲面载荷仿真分析时, 要利用通过试验测得的离散点载荷数据进行加载分析, 其实质就是在曲面上施加离散不均匀分布载荷。

进行曲面离散载荷施加一般有2种方法, 一种是节点插值法, 即提取曲面上各网格节点的坐标, 用有限元软件指定程序语言编制插值程序, 将已知载荷数据按节点坐标进行插值, 然后修改有限元软件脚本语言为相应节点一一赋值, 这种方法精度较高, 但需要用特定语言编制程序, 加载过程复杂; 另一种是函数加载法, 即求出载荷值沿曲面的分布函数并通过函数表达式加载, 这种方法快捷, 但求解载荷分布函数往往比较困难。本文针对工程中常见的由单调曲线回转而成的轴对称曲面上离散载荷的施加问题, 提出了基于曲线拟合和线性插值的曲面函数分区拟合法, 求出载荷值沿各曲面分区的函数表达式, 并通过表达式进行快速有效加载。

1 曲面函数分区拟合与载荷施加

1.1 问题描述

该问题的本质是对载荷值进行曲面拟合[2]。曲面拟合常用的方法是基于最小二乘法的多项式拟合[3-5], 文献[6]还提出了基于三角函数的任意曲线曲面拟合法。这些曲面拟合方法可以较好地解决任意形状曲面拟合问题, 但计算量大, 都需要专门编制程序, 而且随着已知离散点数目的增加, 函数的拟合误差通常会增大。多项式拟合时, 提高函数表达式变量的最高阶次, 可以提高已知离散点处的精度, 但如果阶次过高, 函数会出现明显的振荡, 即Runge现象, 影响非采集数据点的拟合精度。本文针对轴对称曲面, 提出基于曲线拟合和线性插值的曲面函数表达式分区拟合法, 所求出的函数表达式精度高, 计算简单, 便于工程应用。

1.2 曲面函数表达式分区拟合算法

图2 曲面拟合算法示意图

即

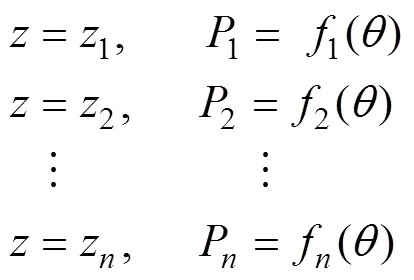
化简得

即为所求式(2)。其他曲面片算法相同。

1.3 拟合精度与算法分析

工程中已知数据点一般通过试验测得, 如压强、高度、温度等变量, 其变化趋势具有连续性, 基于多项式的曲线拟合可以很好地逼近连续性变量的变化趋势, 从而保证了拟合精度。如果局部需要更精确的变量函数表达式, 可以在该处采集更多的离散点, 然后对该处曲面进行细分, 从而拟合出更多沿细分曲面的变量分布函数, 以达到对真实变量分布状况更精确的逼近。

曲线拟合步骤中如果采集的数据点较多, 一般需要提高拟合函数的阶次以保证式(3)的拟合精度。如前所述, 阶次过高会导致函数出现Runge现象, 因此, 应根据实际项目对变量的误差要求和分析结果的安全系数要求, 结合MATLAB曲线拟合工具箱中的Norm of residuals误差显示, 合理选择拟合多项式的阶次。另外, 采用文献[8]中提出的三次样条曲线插值拟合方法,可以在测量点上高精度吻合。

2 实例应用

2.1 测量离散点载荷

模型风洞试验中通过压力传感器测得雷头表面上的离散点压力值(单位MPa), 图3为表面测压点分布图。

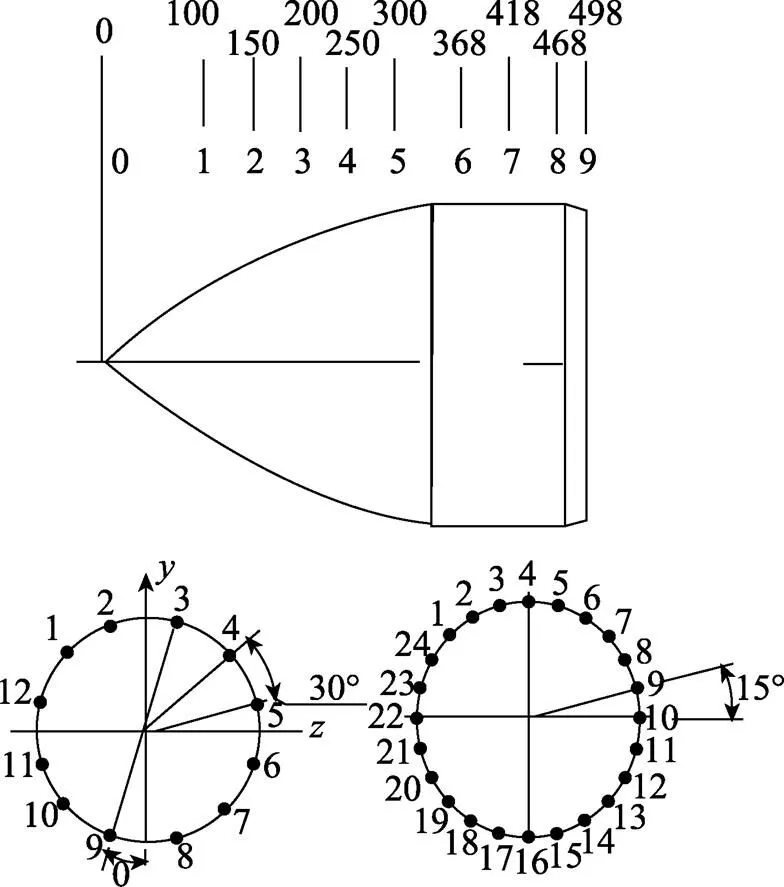
图3 雷头模型风洞试验中测压点分布图

图中, 1, 2, 9号截线上每30°设一测量点, 每条截线设置12个测量点; 3~8号截线上每15°设一测量点, 每条截线设置24个测量点; 雷头顶点设置1个测量点。整个雷头上共设置了181个测量点, 测得了181组不同的压力值。

2.2 算法应用

图4 曲面分区示意图

按照本文算法, 分别对各测压截线上数据进行拟合, 求得9组曲线表达式, 结合雷头顶点处测压值, 共拟合出图中9片曲面的函数, 分别予以加载。加载后的载荷显示如图5所示, Abaqus中用箭头表示载荷, 其中, 箭头方向朝外表示压力为负值, 箭头长度表示压力绝对值大小。

图5 通过函数分区加载示意图

为了验证本方法的精度, 使用传统的手工逐个节点加载方法, 对部分区域进行了离散载荷施加, 设置边界条件后静力分析结果如图6所示; 然后使用本文算法对该区域进行函数加载, 设置相同边界条件后静力分析结果如图7所示。对比应力分布趋势和最大应力值及其出现位置, 可以看出, 在同一坐标方位下, 两者应力分布非常相似, 均在尖端出现了“工”字形高应力区, 最大应力也出现在此位置; 后部为“蛋黄”形低应力区, 应力过渡区域分布也极为相似。考察两者最大应力值, 逐点加载最大应力为

图6 逐个节点加载分析结果云图

图7 本文算法加载分析结果云图

函数加载最大应力为

相对于逐点加载, 函数加载误差为

满足该项目有限元静力分析的精度要求, 也验证了本文所述算法的有效性, 并且相对逐个节点加载, 使用该算法进行函数加载简单高效。

3 结束语

本文针对由单调曲线回转而成的轴对称曲面, 提出了基于曲线拟合和线性插值的曲面分区拟合法, 用于有限元仿真分析中离散分布载荷在曲面上的施加, 经试验验证, 该方法简单有效, 并能保证较高的精度。

本文在柱坐标系中进行曲面拟合, 该方法也可推广到空间直角坐标系中, 用以实现对空间离散值进行分区2D拟合。

本文提出的曲面拟合法, 不仅可以用于正向设计仿真分析, 对逆向工程[11-13](Reverse Engineering)等其他领域也有一定的参考价值。

[1] 林小夏, 张树友, 陈婧, 等. 产品仿真分析中曲面不均匀分布载荷施加方法[J]. 机械工程学报, 2010, 46 (1): 122-127. Lin Xiao-xia, Zhang Shu-you, Chen Jing, et al. Method for Asymmetric Distributed Loads on Curving Areas in Products Simulation Analysis[J]. Journal of Mechanical Engineering, 2010, 46(1): 122-127.

[2] 谷川, 潘国荣. 基坑测斜成果的二维拟合及其三维显示[J]. 铁道勘察, 2005(6): 4-6. Gu Chuan, Pan Guo-rong. The Planar Fitting and 3-D Dis- play of the Deviational Surveying Results of Foundation Pits [J]. Railway Investigation and Surveying, 2005(6): 4-6.

[3] 徐安凤, 李金莱, 姚春光. 非规则三维数据的曲面拟合方法[J]. 计算机工程与应用, 2009, 45(20): 234-239. Xu An-feng, Li Jin-lai, Yao Chun-guang. A Surface Fitting Method for Irregular 3-D Data[J]. Computer Engineering and Applications, 2009, 45(20): 234-235.

[4] 霍晓程, 李小平. 用最小二乘法拟合曲面方程[J]. 赤峰学院学报(自然科学版), 2009, 25(6): 11-13.

[5]石昕, 彭文. 基于加权最小二乘曲面拟合的规则格网DEM建立[J].海洋测绘, 2008, 28(3): 41-44.

Shi Xin, Peng Wen. The Setting-Up of Grid DEM Based on Surface Fitting Using Weighted Least Square[J]. Hydro- graphic Surveying and Charting, 2008, 28(3): 41-44.

[6] 丛伟. 拟合任意空间曲线曲面的三角函数法[J]. 沈阳航空工业学院学报, 2001, 18(1): 69-70. Cong Wei. An Approach to Curve & Surface Modelling based on Triangle Function Method[J]. Journal of Shenyang Insti- tute of Aeronautical Engineering, 2001, 18(1): 69-70.

[7] 陈杰. MATLAB宝典[M]. 2版. 北京: 电子工业出版社, 2010.

[8] 李文升. 基于样条插值的风力机叶片建模[J]. 廊坊师范学院学报(自然科学版), 2010, 10(5): 14-15. LI Wen-sheng. The Modeling for Blades of Wind Turbine Based on Spline[J]. Journal of Langfang Teachers College (Natural Science Edition), 2010, 10(5): 14-15.

[9] 王世忠. 结构力学与有限元法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003.

[10] 庄茁. 基于ABAQUS的有限元分析和应用[M]. 北京: 清华大学出版社, 2009.

[11] 蔚敬斌. 逆向工程研究现状综述[J]. 机械管理开发, 2010, 25(6): 3-4.

Wei Jing-bin. Review of Reverse Engineering Study [J]. Me- chanical Management and Development, 2010, 25(6): 3-4.

[12] 赵勇, 刘丽华, 浦昭邦, 等. 一种新型光纤传感器在逆向工程 中的应用[J]. 仪器仪表学报, 2001, 22(5): 524-526.

Zhao Yong, Liu Li-hua, Pu Zhao-bang, et al. Application of a Novel Fiber-optic Sensor in Reverse Engineering[J]. Chinese Journal of Scientific Instrument, 2001, 22(5): 524-526.

[13] 王伟峰, 廖伟丽, 朱国俊, 等. 基于逆向工程的风力机叶片实体建模研究[J]. 电网与清洁能源, 2008, 24(4): 40-43. Wang Wei-feng, Liao Wei-li, Zhu Guojun, et al. Study of En- tity Modeling for Wind Turbine Blade Based on Reverse En- gineering[J]. Power System and Clean Energy, 2008, 24(4): 40-43.

Method for Imposing Discrete Loads on Curved Surface in Simulation Analysis

XUXin-dong1,2, LI Jian-chen1,2, CAO Xiao-juan1, GONG Ping3

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710075, China; 3. Abaqus Beijing Representative Office, Beijing 100025, China)

To solve the problem of imposing a mass of discretely distributed loads on curved surface, and improve the efficiency and quality of finite element method (FEM) analysis, a subarea polynomial fitting method of curved surface based on curve fitting and linear interpolation is proposed. With axisymmetric curved surface revolved by a monotonous curve, the functions of the discrete loads along the surface subareas are derived, then the loads are imposed on the whole curved surface through the functions for simulation analysis. Hence, the efficiency of pre-process for the FEM is enhanced. The simulation of model wind tunnel test indicates that this method is simple and effective with high precision.

finite element method(FEM); discretely distributedload; subarea polynomial fitting method of curved surface; simulation

TJ631.2; TM46

A

1673-1948(2011)04-0246-04

2011-05-23;

2011-06-15.

徐新栋(1984-), 男, 在读硕士, 研究方向为武器系统总体技术.

(责任编辑: 陈 曦)