脉冲噪声环境下编码信道抗噪声性能研究*
姚 娟,万 瑶,李丽芳,张 谦
(中北大学信息与通信工程学院,山西太原030051)
0 引言
传统的信号处理理论和技术基本上是基于高斯分布和二阶统计量的,其重要原因之一是当时缺乏对更复杂信号噪声模型进行分析和处理的工具。随着计算机技术和信号处理理论的迅速发展,人们已有能力对更复杂的模型进行分析和处理,非高斯信号处理的理论和技术得到了迅速的发展和广泛的应用。本文将以α稳定分布和信道编码理论为基础,采用α稳定分布噪声模型,对脉冲噪声环境下编码信道的抗噪声性能进行研究。
1 信道编码
信道编码[1]是在信息码中增加一定数量的可控制冗余码元(称为监督码元),使信息码元和冗余码元之间满足一定的约束关系,当传输过程中出现差错时约束关系被破坏,在接收端按照既定的规则校验,恢复出正确的数据序列,从而达到纠错的目的。
分组码[2]是一组固定长度的码组,可表示为(n,k)。在编码时,k个信息位被编为n位码组长度,而n-k个监督位的作用就是实现检错与纠错。信息码元与监督码元成线性关系时的分组码称为线性分组码。循环码就是一类重要的线性分组码,因其代数构造和线性反馈移位寄存器的数学构造相同,使其编译码器可以由线性反馈移位寄存器实现,常将码长为n的码组表示为代数形式
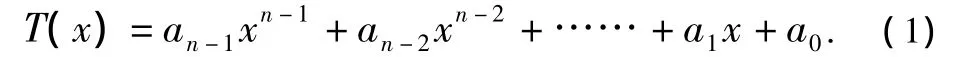
卷积码[3]是由连续输入的信息序列得到连续输出的已编码序列。卷积码至今尚未找到严密的数学手段,把纠错性能与码的结构十分有规律地联系起来,目前大多采用计算机来进行编码。卷积码编码后的n个码元不仅与当前段的k个信息有关,而且还与前面N段的信息有关。卷积码编码器一般由N个1位的移位寄存器及n个模2和加法器组成。
2 α稳定分布
α稳定分布的概念最先是由利维(Levy)于1925年给出的。近年来,α稳定分布和相应分数低阶统计量理论研究和应用为不同领域的许多现象提供了非常有用的模型。
2.1 α稳定分布的定义
如果对于任何正数A和B,存在正数C和一个实数D,满足

则随机变量X是稳定分布的。式中,X1和X2为X的独立样本,符号“=d”表示分布相同。α稳定分布[4]没有统一的封闭的概率密度函数,通常用其特征函数式(3)来描述
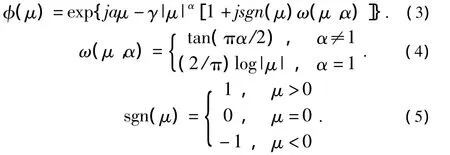
式中:(1)α∈(0,2]为特征指数,表示α稳定分布概率密度函数拖尾的厚度;(2)γ>0为分散系数,表示分布的分散程度;(3)β∈[-1,1]为对称参数,当β=0时称为对称α稳定分布,记为SαS;(4)a∈(-∞,∞)为位置参数,对于SαS,a表示分布的均值或中值。
α稳定分布随机变量的概率密度存在且连续,但除了少数例外之外,它们没有封闭的形式。这种例外包括高斯分布N(μ,2σ2)(其中 μ =α,σ2=γ/2),其密度函数为:
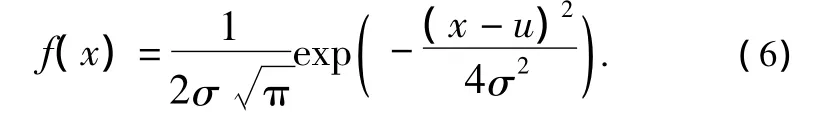
由式(3)可知,当α=2时,α稳定分布与高斯分布的特征函数完全相同,因此认为α稳定分布是广义的高斯分布,并定义0<α<2的α稳定分布为分数低阶α稳定分布。
α稳定分布作为建模工具非常灵活,主要原因在于它的特征指数α可以用于控制概率密度函数拖尾的厚度。α值越小,表明所对应的信号噪声中有越显著的尖峰脉冲;α越接近2,则更接近高斯特性;当α=2时,则为高斯分布。
2.2 α稳定分布随机变量的算法
假定我们要产生阶数为α(0<α≤2)的α稳定分布序列x(n),满足a=0和-1<β<1。定义:

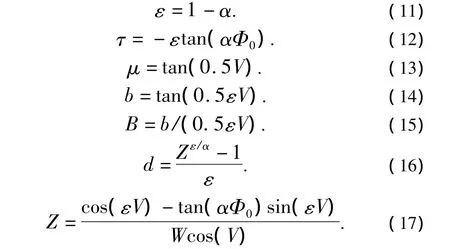
这样,满足给定α值的分数低阶α稳定分布的随机变量X[5]由式(18)给出

2.3 分数低阶α稳定分布噪声条件下混合信噪比的设定
在分数低阶α稳定分布噪声条件下,由于不存在有限的二阶矩,致使噪声的方差变得没有意义,因此需要采用混合信噪比。混合信噪比定义为:


式中,s(n)为按照给定信噪比调整幅度后的信号,Var[s'(n)]表示信噪比设定之前信号的方差。按照式(21)调整给定信号s'(n)的幅度,就可以实现设定信噪比的目的。
3 α稳定分布噪声下编码信道抗噪声性能分析
3.1 α稳定分布噪声的产生
在使用分数低阶α稳定分布作脉冲噪声模型时,不失一般性的,常设参数μ=0,α=1,β=0。由式(18)可获得一个包含参数α、β、γ、μ的随机变量 X,循环便得到 x(n)序列。当给定混合信噪比m时,若已知信号方差,根据式(19)即可求得γ,

将以上各参数代入式(18),即可获得脉冲噪声。以下是β=0、γ=1、μ=0的不同α下的噪声波形。

图1 α=0.9时的噪声波形
图2 α=1.5时的噪声波形

图3 高斯噪声(α=2)
3.2 信道编码与译码的实现
MATLAB中进行信道编译码非常方便,循环编码时可以应用函数 encode,译码则应用decode,并根据需要设置为“cyclic”编码方式。卷积编码时先应用函数poly2trellis定义一个trellis矩阵,再用convenc进行编码,译码时使用维特比译码方法,可应用函数vitdec。译码后可以直接应用函数symerr计算出误码率,并进行抗噪声性能的比较。
3.3 抗噪声性能分析
当信息码元一致时,在循环码编码信道条件下,分别加入α稳定分布噪声和高斯噪声,译码后对误码率进行比较。由图4可知:当0<MSNR<20 dB时,高斯噪声误码率小于脉冲噪声的误码率,且脉冲噪声α=1.5时的误码率小于α=0.9时的误码率;当误码率开始为0时,高斯噪声,α=1.5和 α =0.9 的脉冲噪声的MSNR 分别为6 dB,9.2 dB,16.4 dB。由此可知,相同条件下,脉冲噪声所造成的误码影响比高斯噪声所造成的误码影响大得多,且脉冲噪声的α越小,误码率越大。

图4 循环码编码信道下的误码率比较(β=0,μ=0)
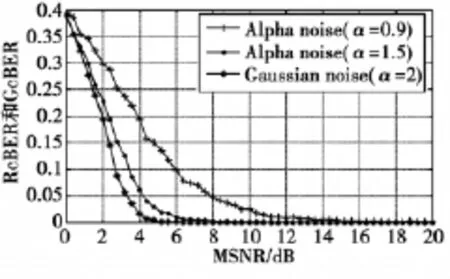
图5 卷积码编码信道下的误码率比较(β=0,μ=0)
同样的,当信息码元一致时,在卷积码编码信道条件下,分别加入α稳定分布噪声和高斯噪声,译码后对误码率进行比较。由图5可知:当0<MSNR<20 dB时,高斯噪声误码率小于脉冲噪声的误码率,且脉冲噪声α=1.5时的误码率小于α=0.9时的误码率;当误码率开始为0时,高斯噪声,α=1.5和 α=0.9的脉冲噪声的 MSNR 分别为 5.2 dB,9.2 dB,16 dB。由此可知,相同条件下,脉冲噪声所造成的误码影响比高斯噪声所造成的误码影响大得多,且脉冲噪声的α越小,误码率越大。此结论与图5得出的结论相同。
4 结论
本文分析总结了编码信道及α稳定分布的基础理论,并以α稳定分布噪声为脉冲噪声模型,研究了脉冲噪声环境下编码信道的抗噪声性能,并同高斯噪声下的编码信道性能相比较。仿真结果表明,相同条件下,高斯噪声所造成的误码影响比脉冲噪声所造成的误码影响小得多;且当脉冲噪声的参数β、γ、μ相同,α越小时,拖尾越长,脉冲噪声所造成的误码率越大;高斯噪声所造成的误码率在信噪比较小的情况下即可达到零,远小于脉冲噪声所要求的信噪比。
[1]赵晓群.现代编码理论[M].武汉:华中科技大学出版社,2008.
[2]樊昌信,曹丽娜.通信原理[M].第6版.北京:国防工业出版社,2008.
[3]王育民,李晖,梁传甲.信息论与编码理论[M].北京:高等教育出版社,2005.
[4]罗鹏飞.统计信号处理[M].北京:电子工业出版社,2009.
[5]邱天爽,张旭秀,李小兵,等.统计信号处理——非高斯信号处理及其应用[M].北京:电子工业出版社,2004.

