卷积编码的识别技术研究
杨树树,刘旭波,徐学华,李贵显,冀贞海
(1.中国航天科工集团8511研究所,江苏 南京 210007; 2.中国人民解放军91977部队,北京 100142)
0 引言
现代数字通信系统中为了对抗各种形式的干扰,保证信息传输的有效性与可靠性,通常会采用信道编码技术[1]。在合作通信领域,收发双方预先知道信道编码的方式及其编码参数,接收方可以根据这些先验信息进行信道解码,恢复发送方的信源信息;在非合作通信领域,通信参数是很难预先获得的,需要通过对信道编码的识别分析来获取[2]。
信道编码的识别技术目前已成为非合作通信领域的重要研究方向,广泛应用于智能通信(也叫认知通信)、通信侦察和网络对抗等领域。在未来的智能移动通信、多点广播通信中,将广泛采用自适应调制编码技术,随着时间和环境的变化需要随时改变信道编码方式,以便获得最优的通信效率和服务质量,为了在收发双方快速建立通信连接,需要接收方仅根据接收的未知数据快速识别出信道编码的体制、参数,以达到智能通信的目的;在非合作通信侦察领域,通过信道编码识别技术识别截获数据的编码方式和编码体质,将截获的敌方数据序列进行译码,最终得到更多的敌方信息;在网络对抗领域,当对方网络信源和通信协议加密时,从信道编码结构上进行攻击是可供选择的有限手段之一[2-5]。
目前常用的信道编码类型有BCH码、RS码、卷积码、LDPC码和Turbo码等。其中,卷积码具有纠错能力强和编译简单等优点,在卫星通信系统、深空探测系统中得到了广泛应用[6-8]。因此,卷积码的识别对于空间信息对抗具有十分重要的意义,本文针对卷积码的识别技术进行研究。
1 卷积码的基本概念
卷积码由美国麻省理工学院的埃里亚斯(Elias)于1955年提出,卷积码可以看作一种特殊的分组码,具有分组码的一些基本特点[2],同时卷积码还有自身的一些特殊性质。分组码编码时,本组的n-k个校验元仅与本组的k个信息元有关,而与其他各组码元无关;译码时也仅从本组的码元中提取译码信息。卷积码则不同,它是一个有限的记忆系统,卷积码编码时,本组的n-k个校验元不仅与本组的k个信息元有关,还与以前各个时刻输入至编码器的信息元有关;译码时不仅从此时刻收到的码组中提取译码信息,而且还要从之前和之后各时刻收到的码组中提取有关信息。此外,卷积码中每组的信息位k和码长n,通常要比分组码的k和n小,卷积码无论是编码还是译码,复杂度决定了k和n不可能很大,实际应用中的n一般不超过8。
卷积码一般可以用(n,k,m)来表示,其中,n:编码器输出码元的位数,即编码长度;k:编码器输入码元的位数,即信息位的数目;m:约束长度,即编码时移位寄存器的个数;R=k/n:编码效率,即码率;N=n(m+1):编码约束长度,表示编码过程中互相约束的码元的个数。
无论分组码还是卷积码,它们都是由生成矩阵或校验矩阵决定的,用什么样的生成矩阵对信息进行编码就会产生什么样的码字。反过来,接收方接收的信息码字也一定符合发送方所采用的码的校验矩阵。
卷积码的生成矩阵可以表示成:
(1)
与分组码的不同是,卷积码的生成矩阵是一个半无限矩阵,生成矩阵的每k行都是由g=(g0,g1,g2,…gm)右移n位得到,G∞完全由g决定,因此g称为基本生成矩阵,卷积码可以认为是由g线性移位相加得到的。
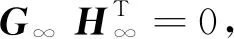
(2)
2 卷积码的识别参数
卷积码的识别分析需要识别的未知参数包括:码字起点α,码长n,码率R,基本生成矩阵g,校验矩阵H,基本生成多项式g(x)等。
码字起点α:待分析的识别序列数据中,卷积码字的起始点是未知的,以α表示数据序列中起始点在卷积码字中的位置,1≤α≤n。
码长n:识别分析所有参数中最关键的一个参数。
码率R:用k/n表示,表征编码效率或传输效率。
基本生成矩阵g:g=(g0,g1,g2,…gm),这是识别分析的目标,得到了g,也就基本完成了任务。
校验矩阵H:由CHT= 0,通过识别分析最先得到该参数,是识别分析的起点,其中C为编码后的识别序列数据。
生成多项式g(x):用来表示卷积码编码器的多项式集合。
3 卷积码识别技术3.1 无误码条件下的系统卷积码识别
由于卷积码可以看作特殊的线性分组码,因此卷积码的识别方法可以利用线性分组码的方法。比较系统卷积码和系统线性分组码的生成矩阵的区别,可以发现卷积码也有类似的结构,也就是说将卷积码的编码序列排成n阶方阵,对其进行行初等变换单位化也能得到 [IkP],但是这个矩阵并不能完整描述一种卷积码,其中的p只是卷积码的部分校验序列,完整的卷积码校验序列一共有m个这样的序列,这是卷积码的记忆性造成,也就是本分组的信息不仅和本分组有关还与相邻的m段信息有关,根据这个特点可构造如图1所示的矩阵模型。

图1 卷积码识别矩阵模型
与线性分组码不同之处在于矩阵的列数y要求大于N=n(m+1),同样也要求行数x>y,由于卷积码的n和k一般都很小,所以y一般取64就足够了。码长n最大不超过8,因此最小公倍数d=840[4],即矩阵每行起点位置的码元在序列中的位置相差840。
对构造的矩阵进行行初等变换单位化得到以下形式:
(3)
式(3)就是系统卷积码的生成矩阵形式,根据该矩阵就可以得出卷积码n,k,m,α以及校验向量等参数。其中p0,p1,..pm叫做卷积码的校验向量,可以得到该卷积码的校验矩阵,对于系统卷积码进而可以得到生成矩阵。
3.2 无误码条件下的非系统卷积码识别
对于非系统卷积码而言同样也可以得到如式(3)所示的矩阵形式,这是由于非系统的线性分组码的生成矩阵总能通过行初等变换变成系统线性分组码的生成矩阵的形式,但是这个形式不代表非系统卷积码的生成矩阵。对于非系统卷积码同一个校验矩阵可以对应多个生成矩阵,因此对于非系统卷积码,该方法只能得到n,k,m,α和校验向量p0,p1,…,pm。如果要得到生成矩阵还要作进一步分析,对于某些类型的卷积码在得到了n,k,m后是比较容易得到生成矩阵的。
非系统卷积码由于性能较好,大多数实用的卷积码都是非系统卷积码,下面研究一种比较特殊的非系统卷积码,即1/2码率的非系统卷积码。这种卷积码具有代表性,并且可以利用1/2码率的非系统卷积码的识别方法解决所有1/n非系统卷积码的识别问题。
3.2.1 1/2非系统卷积码的识别
1/2卷积码的生成矩阵为:
G(D)=[g1(D)g2(D)]
(4)
校验矩阵为:
H(D)=[h1(D)h2(D)]
(5)
根据G(D)·H(D)T=0得:
g1(D)=h2(D),g2(D)=h1(D)
(6)
由式(6)可知只要得到了校验矩阵也就得到了生成矩阵,对1/2的这种特殊非系统卷积码而言,校验矩阵和生成矩阵之间是一一对应的关系,因此对1/2码率的非系统卷积码识别是可行的。
3.2.2 1/n非系统卷积码的识别
首先不管是何种码率的非系统卷积码都可以利用3.1节中的方法得到n,k,m,α。如果通过识别得知该卷积码为1/n卷积码则可利用1/2卷积码的方法来进行识别,得到生成矩阵。
具体方法如下:
1)将1/n卷积码的数据码字利用之前识别得到的α值确定数据的码字起始位置。
2)将数据分解成几个1/2非系统卷积码,因为从结构上来说1/n非系统卷积码都可以认为是若干个1/2非系统卷积码复合而成,并且相互之间是独立的。
3)分别对上述几个1/2非系统卷积码进行识别,得到其生成矩阵。由于n,k,m,a都已知,因此所需要的数据量大大减小。
3.2.3k≥2非系统卷积码的识别
对于k≥2的情况,只能识别出部分参数,目前还没有有效的方法得到生成矩阵G。
3.3 有误码条件下的非系统卷积码识别
现实条件下,解调特别是盲解调中误码是不可避免的,因此必须讨论在有误码条件下目前所采用的算法的可行性。毫无疑问误码会破坏原有码字之间的线性关系,也就是说在有误码条件下所得到的识别矩阵在进行行初等变换单位化处理后不一定能提取出正确的参数信息,这里面包括可能会得到错误的n,k,m,α或者校验序列。
有误码条件下的主要策略为:
1)先验信息的获取很重要,在未知n,k,m,α等先验信息的时候通常需要较多的数据量,数据量越多遇到的错误比特越多,越不容易得到正确的结果。
2)可以取多组数据进行分析,根据大数判决的原理取信出现概率大的结果,结合去除一些不合理结果(α>k,n,k,m的取值不合理等)的方法尽量正确估计n,k,m,α等信息。
3)根据已经得到的先验信息,减少数据量再次进行识别,并再次多次计算大数判决提高识别率。
有误码条件下的卷积码具体识别的流程图如图2所示。
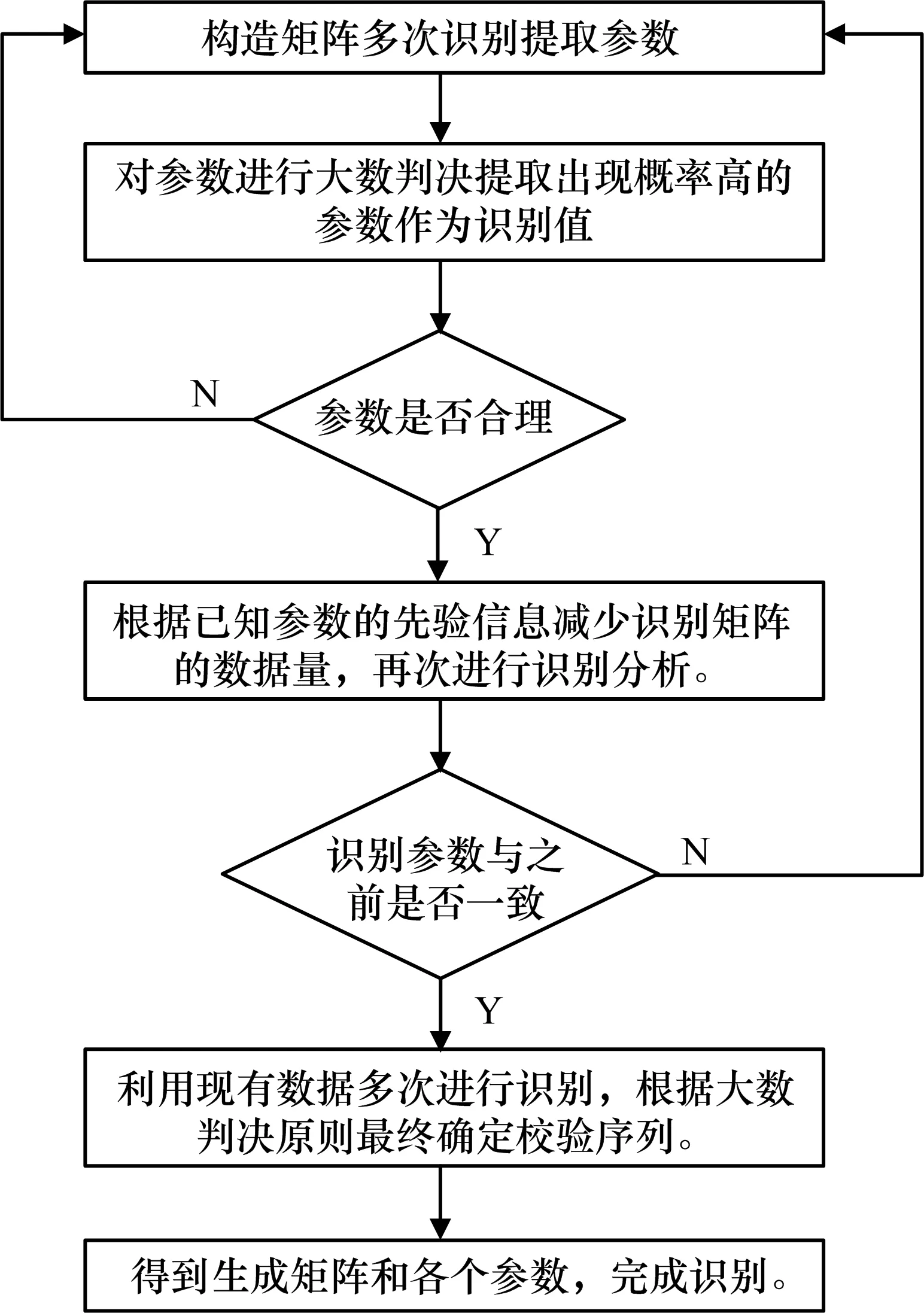
图2 有误码条件下卷积码识别流程图
4 卷积码识别分析仿真实验
由上述分析可知1/2码率的非系统卷积码是一种具有代表性的非系统卷积码,取最常见的(2,1,6)的1/2非系统卷积码来进行仿真。仿真参数如下:n=2,k=1,m=6,α=1,G1=133,G2=171,样本数为1000。
图3是BPSK调制加高斯白噪声条件下Eb/N0和识别率之间的关系曲线。
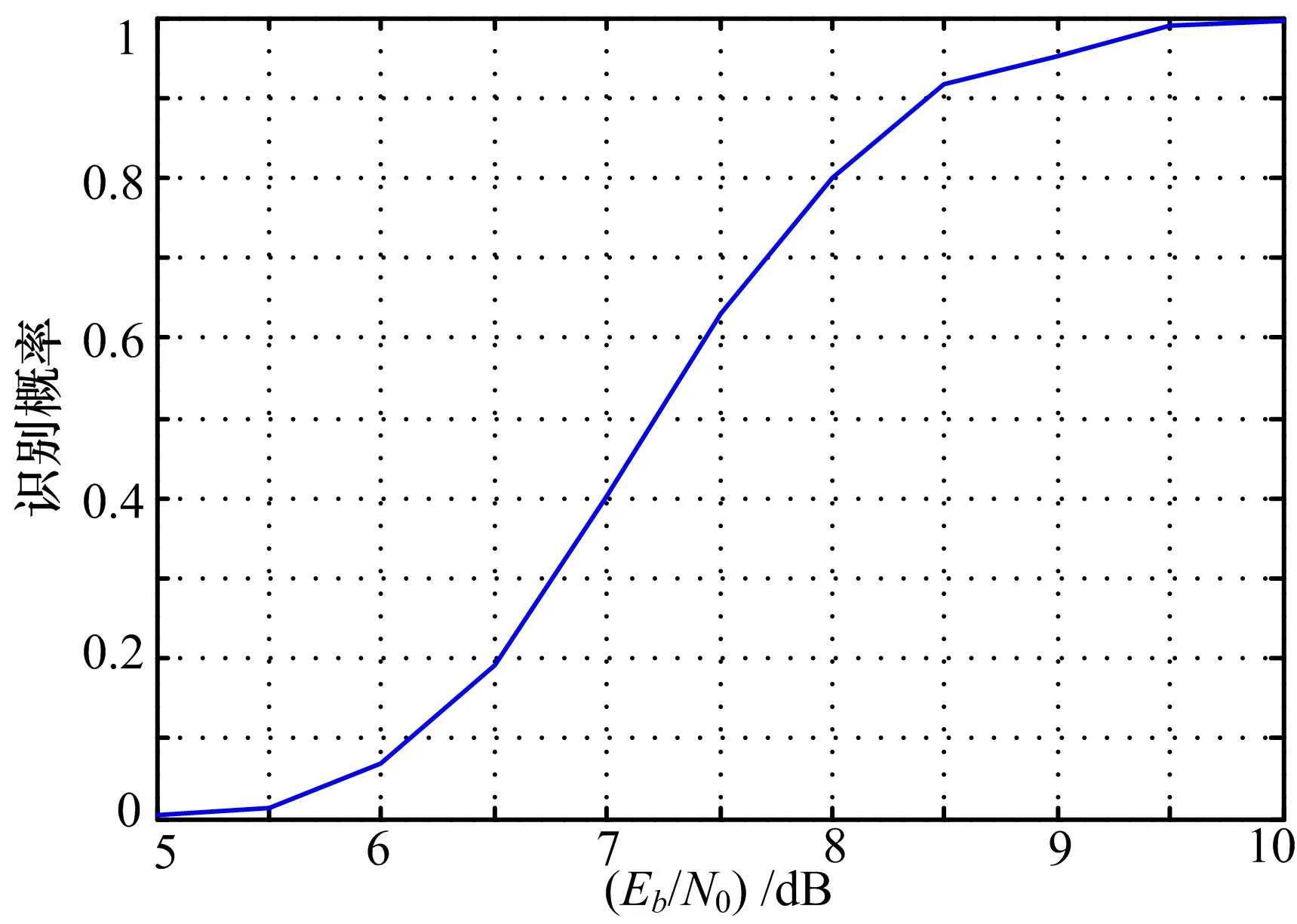
图3 BPSK调制下Eb/N0和识别率之间的关系曲线
图4是硬判决误码率和识别率曲线之间的关系。
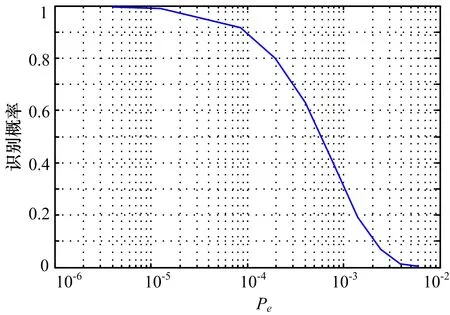
图4 解调硬判决误码率和识别率之间的关系曲线
由仿真结果可知,当Eb/N0≥6.5 dB时,识别率大于20%,这时候如果多次取样进行识别,再利用大数判决会有较大概率得到正确的估计值。
实际操作时采样的次数不可能太多,取20次进行仿真。按照20次识别结果判决,重复10次,表1是判决结果和Eb/N0之间的关系表。

表1 多次识别判决的识别率与Eb/N0的关系表
比较表1和图3可知,单次识别在Eb/N0=7 dB 时识别率约为40%,采用多次识别结果进行判决后识别率几乎达到了100%;单次识别在Eb/N0=5.5 dB时仅为1.3%,采用多次识别结果进行判决后识别率达到了20%。可见这种方法利用了更多的数据和更大的运算量提高了识别的准确率,更加准确的识别结果为后续工作打下了良好基础。
当得到估计值后,利用估计值可以减小数据量,当n,k,m,α都已知的时候,d取n即可,数据量只需要y+xn个比特;再次进行识别,由于数据样本少,碰到样本数据全对的概率增大,得到的结果会更可靠。由于数据量减小了,可以再次利用数据作多次估计,再根据所得矩阵,判断校验序列中相应位置0和1出现的概率,最后得到较为可靠的校验序列,从而估计出卷积码的生成矩阵G。
5 结束语
本文介绍了卷积码的基本概念,对卷积码的识别技术进行了研究,卷积码本质上是一种特殊的线性分组码,可以借鉴线性分组码的识别方法对卷积码进行识别分析;重点研究了无误码条件下系统卷积码和非系统卷积码的识别方法,以及有误码条件下的非系统卷积码识别方法,并对有误码条件下非系统卷积码识别进行了仿真分析。仿真结果说明,在有误码率的条件下,根据大数判决的原理结合多次识别的方法相对单次判决识别性能有大幅提升。

