不同流变模型下的淤泥与波浪相互作用规律

白玉川，田 琦

(天津大学建筑工程学院河流海岸泥沙研究室，天津 300072)

不同流变模型下的淤泥与波浪相互作用规律

白玉川，田 琦

(天津大学建筑工程学院河流海岸泥沙研究室，天津 300072)

建立波浪在淤泥质底床上传播的理论模型并对其进行求解，讨论了淤泥质河口海岸中淤泥与波浪的相互作用规律，包括波浪作用下的淤泥输移规律以及波浪在淤泥质床面上传播过程中的衰减现象.根据计算得出不同底床密度下，水层和泥层的流速和压强分布，分析波浪衰减的影响因素，针对3种不同的淤泥流变模型(黏性流体模型、幂律流体模型和黏弹性介质模型)，分别计算相应的波浪衰减值，并与实验值进行对比.结果显示，选用的淤泥的流变模型不同，泥床对波浪的衰减值也不同.影响波浪衰减的因素主要有泥厚、波浪周期以及水深.泥厚和波浪周期均存在临界值，使波浪衰减达到最大；衰减率随水深的增大而单调减小.通过与实测值比较得出幂律流体模型更能描述淤泥的真实情况.

河口；淤泥；流变模型；波浪衰减

淤泥质河口、海岸环境中的波流动力因素和泥沙运动规律十分复杂，波浪既可以引起浮泥的波动、悬扬、输移，浮泥也可以反过来影响波浪的传播与衰减.波浪在淤泥质床面上传播时引起惊人的能量衰减：印度的Kerala在西南季风里，入射到淤泥滩上的台风浪只需4～8个波长的距离就可完全被衰减掉[1]，由淤泥运动引起的表面波浪的能量损失至少比渗透或摩擦引起的损失高 1个量级；钱宁等[2]描述了我国黄河口烂泥湾的消波现象，指出波浪经过烂泥湾后波高减少了很多，该地因而成为渔民的避风港.针对波浪与泥质床面相互作用及其迅速衰减的现象，国内外研究工作者按床面淤泥本构关系的不同，建立了多种理论模型，主要有：①黏性流体模型；②黏塑性体模型；③黏弹性介质模型；④黏弹塑性介质模型；⑤边带阻尼模型；⑥多孔介质模型.这些理论模型取得了重要的研究成果：Macpherson[1]几乎同时用 voigt线性黏弹性模型研究泥床上的波浪衰减；Maa等[3]把黏性泥床分成多层线性黏弹性泥层，在恒定密度、黏度和弹性模量的条件下模拟随深度变化的床面特性和能量耗散；吴永胜等[4]引入了淤泥床面上波浪边界层以及波浪紊动的变化特性，分析了波浪边界层厚度，泥层 stokes边界层厚度以及泥层振幅相位滞后与波浪衰减率之间的关系；白玉川等[5]进行了波浪在泥床上衰减规律的实验研究，并利用量纲分析及逐步多元回归的统计学方法，建立了便于工程实际应用的波浪衰减规律公式；赵子丹等[6-7]在泥层为宾汉流体假定下，对界面波振幅、泥层内的轨迹速度和波浪的沿程衰减做了实验验证；练继建[8]对水流、波浪与淤泥质底床的相互作用问题进行了系统的理论分析和实验研究；张庆河[9]建立多层模型描述波浪与泥床的相互作用.Zhang和 Ng[10-11]将淤泥看作黏弹性体建立两层 Stokes边界层模型讨论波浪衰减以及交界面波幅与相位差的影响因素.近期学者[12-13]通过建立Boussinesq型方程组来描述波-泥相互作用下水波的传播.考虑到淤泥流变特性的非线性影响，笔者分别讨论了 3种不同的流变模型下的波浪与淤泥质底床的相互作用.

1 基本方程

1.1 控制方程

图1 波浪在淤泥床上的传播示意Fig.1 Spread of wave in mud bed

波浪在淤泥床上的传播如图 1所示.以静水面为x轴，波浪传播方向为正，垂直方向为y轴，建立坐标系，水深为h，泥厚为d，水面的位移η＝a exp[i(kxσt)]及交界面的位移 ξ＝b exp[i(kx-σt)]，建立连续方程和运动方程，即

1.2 边界条件

1.3 方程求解

设式(1)～式(3)对于Uj、Vj和Pj有如下形式解

式中k为待求的复波数，k＝kr+iki，其实部kr为波数，虚部 ki为波浪衰减率，将式(14)～式(16)代入式(1)～式(3)，可得到

式(22)～式(31)共有 10个方程，含有待求复波数 k、交界面振幅 b以及待定系数 A～H，一共 10个未知数，因此方程组是适定的，当方程组的系数行列式的值为零，方程组有非零解.行列式值 Δ＝0即波动的色散关系

给定其他参数，则色散关系是关于 k的超越方程，用 Muller法求解特征值 k，当求得 k后代回式(22)～式(31)，用高斯消去法求得各待定系数 A～H及b，进而求得流速、压力分布.

2 结果分析

2.1 波浪作用下的淤泥输移

根据规则波在淤泥质底床面上传播的理论模型，计算出不同底泥床面密度下，水层和泥层的流速、压力分布，如图2～图4所示.可以看出，泥层的水平速度小于水层的速度，且在交界面处不连续，随着泥床密度的减小，水泥交界面处的流速梯度也减小，剪应力也相应减小.泥层和水层的垂向速度连续增加.

泥水交界面处压力不连续，随着泥层密度的不同，压力呈现出：①在界面处泥层的压力小于水层的压力(如密度为1 400,kg/m3)；②在界面处泥层的压力大于水层的压力(如密度为1 200,kg/m3).

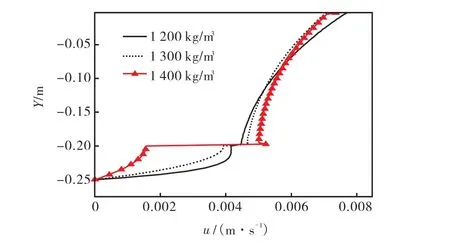
图2 不同密度下水层和泥床的水平速度分布Fig.2 Horizontal velocity of water and mud layers under different densities

对于泥床密度2ρ＝1,400,kg/m3条件下，比较3种流变模式的水层和泥层的流速、压力分布，从图 5～图 7中可以看出，不同流变模式下流速、压力分布趋势基本相同，数值上存在一些差异，跟实测值比较后得知幂律流与实测值更接近.

图3 不同密度下水层和泥床的垂向速度分布Fig.3 Vertical velocity of water and mud layers under different densities

图4 不同密度下水层和泥床的压力分布Fig.4 Pressure distribution of water and mud layers under different densities

图5 不同流变模式的水层和泥床的水平速度分布Fig.5 Horizontal velocity of water and mud layers under different rheological models

图6 不同流变模式的水层和泥床的垂向速度分布Fig.6 Vertical velocity of water and mud layers under different rheological models

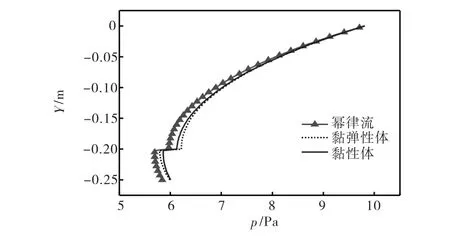
图7 不同流变模式的水层和泥床的压力分布Fig.7 Pressure distribution of water and mud layers under different models

2.2 淤泥质床面上的波浪衰减

通过对波浪衰减率的理论计算结果进行分析发现，泥厚、水深、波浪周期和流变模型对波浪衰减率都有影响.从图 8中可以看出，运动黏度存在临界值，使波浪衰减达到最大，小于或大于该运动黏度，波浪衰减率都减小；从图 9中可以看出，衰减率随水深的增大而单调减小；从图 10中可以看出，在泥厚较小时，衰减率随泥厚的增大而迅速增大，当泥厚增大到某个值，衰减率达到最大，若继续增加，波浪衰减率将缓慢减小，随泥黏性的增大，出现最大衰减率的泥厚也增大；从图 11中可以看出，不同床面密度下随波周期的增大，波浪衰减率增大，但达到某一周期后，即呈下降趋势.

图8 波浪衰减率与泥层运动黏度的关系Fig.8 Relationship between wave attenuation and kinematic viscosity

图9 不同密度下波浪衰减率与水深的关系Fig.9 Relationship between wave attenuation and water depth under different densities

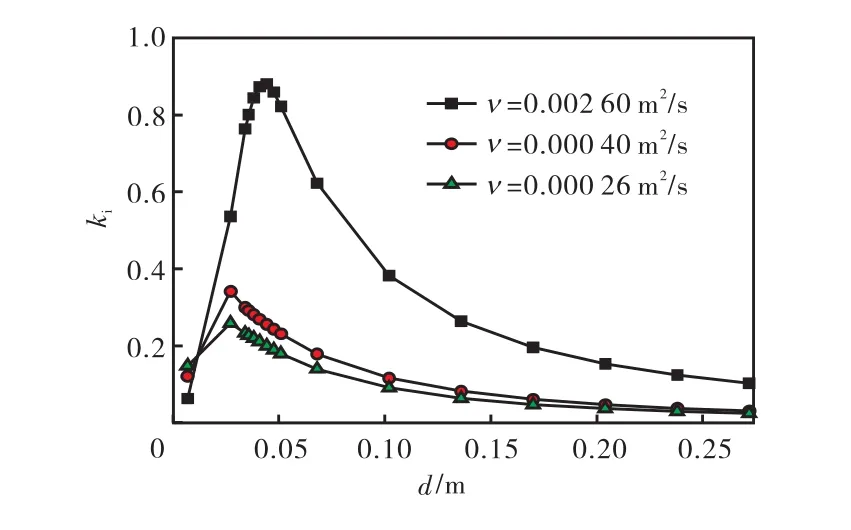
图10 不同运动黏度波浪衰减率与泥厚的关系Fig.10 Relationship between wave attenuation and mud thickness under different kinematic viscosity

图11 不同密度下衰减率随波周期的变化规律Fig.11 Relationship between wave attenuation and wave period under different densities

为验证理论模型，将计算值与练继建等[7-8]的实测值进行对比，实验装置如图 12所示.波浪衰减实验是在长32,m、宽50,cm、高50,cm的波浪水槽中进行的，水槽尾部设有消波装置.实验段位于水槽中部，为长 9.3,m 的凹槽，泥层是搅拌后经静水自然沉降而形成的.在试验段布置4个波高传感器，传感距离分别为 3,m、3,m、2,m，实测波浪指数衰减率由沿程4点波高拟合而得到，首尾传感器距离实验段首尾分别为 0.7,m和 0.6,m，以消除实验段端部的影响，波浪的测量是利用计算机实施同步测量 4点波形而实现的，采样时间间隔为 0.05,s，取样时间一般为 25,s左右，测点波高由实测时间段内多个波浪的波高平均而得到.

表1 波浪衰减率的实验值与理论值的比较Tab.1 Comparison between calculated and measured values of wave attenuation

表1列出了所有的实验条件、实验结果以及不同流变模型下的波浪衰减率的理论计算值，图 13比较了不同淤泥流变模型的波浪衰减计算值与实测值，可以看出，幂律流模型与实测值更接近，能更好地描述淤泥床面的真实性质.

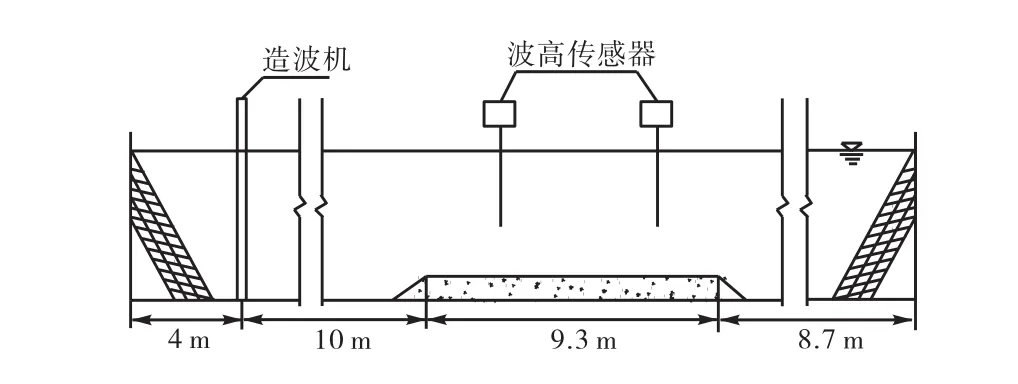
图12 实验布置示意Fig.12 Sketch of experimental facilities

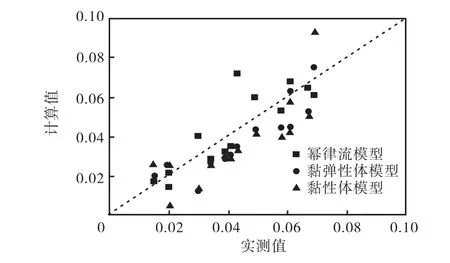
图13 3种不同模型计算值与实测值的比较Fig.13 Comparision between measured values and calcu-Fig.13 lated values in three rheological models

3 结 语

泥层的水平速度小于水层的速度，且在交界面处不连续，随着泥床密度的减小，水泥交界面处的流速梯度也减小，剪应力也相应减小；泥层和水层的垂向速度连续增加；泥水交界面处压力不连续，随着泥层密度的不同，压力呈现出两种不同的趋势：①在界面处泥层的压力小于水层的压力；②在界面处泥层的压力大于水层的压力.在不同流变模式下水层和泥层的流速、压强分布趋势基本相同，数值上存在一些差异，跟实测值比较后得知幂律流与实测值更接近.泥厚、水深、波浪周期是影响波浪衰减率的主要因素.泥厚和波浪周期都存在临界值，使波浪衰减达到最大，小于或大于该值，波浪衰减率都减小；衰减率随水深的增大而单调减小.

［1］Macpherson H. The attenuation of water wave over a non-rigid bed[J].Journal of Fluid Mechanics，1980，97(4)：721-742.

［2］钱 宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，2003.

Qian Ning，Wan Zhaohui. Mechanics of Sediment Transport[M]. Beijing：Science Press，2003(in Chinese).

［3］Maa J P Y，Mehta A J. Soft mud response to water waves[J].Journal of Waterway，Port，Coastal and Ocean Engineering，ASCE，1990，116(5)：634-650.

［4］吴永胜，王兆印，胡世雄. 淤泥对波浪衰减作用的数值模拟[J]. 水利学报，2003(7)：22-29.

Wu Yongsheng，Wang Zhaoyin，Hu Shixiong. Numerical modeling of wave damping over muddy bed[J].Journal of Hydraulic Engineering，2003(7)：22-29(in Chinese).

［5］白玉川，胡世雄，金玉石. 泥质床面上波浪衰减规律的研究[J]. 水利学报，2001(11)：56-61.

Bai Yuchuan，Hu Shixiong，Jin Yushi. Study on the rule of wave decaying on silt seabed[J].Journal of Hydraulic Engineering，2001(11)：56-61(in Chinese).

［6］姜 林，赵子丹. 浮泥海床上孤立波的黏滞衰减[J].水动力学研究与进展，A 辑，1989，4(1)：51-64.

Jiang Lin，Zhao Zidan. Viscous damping of solitary waves over fluid-mud seabed[J].Journal of Hydrodynamics，Ser A，1989，4(1)：51-64(in Chinese).

［7］赵子丹，练继建. 波浪在淤泥质床面上传播时波要素的变化[J]. 天津大学学报，1994，27(5)：521-528.

Zhao Zidan，Lian Jijian. On the change of wave parameters for water waves propagating over a muddy bottom[J].Journal of Tianjin University，1994，27(5)：521-528(in Chinese).

［8］练继建. 波浪、水流与淤泥质底床的相互作用[D]. 天津：天津大学建筑工程学院，1993.

Lian Jijian. Interactions Among Waves，Currents and Muddy Bottoms[D]. Tianjin：School of Civil Engineering，Tianjin University，1993(in Chinese).

［9］张庆河. 规则波、不规则波与淤泥质底床的相互作用[D]. 天津：天津大学建筑工学院，1994.

Zhang Qinghe. Interaction Between Regular or Irregular Waves and Muddy Bottoms[D]. Tianjin：School of Civil Engineering，Tianjin University，1994(in Chinese).

［10］Zhang X Y，Ng C O. Mud-wave interaction：A viscoelastic model[J].China Ocean Engineering，2006，20(1)：15-26.

［11］Ng C O. Water waves over a muddy bed：A two-layer Stokes’ boundary layer model[J].Coastal Engineering，2000，40(3)：221-242.

［12］Liu P L-F，Chan I-C. On long-wave propagation over a fluid-mud seabed[J].Journal of Fluid Mechanics，2007，579：467-480.

［13］夏乐章，朱克勤. Maxwell泥床上线性长波衰减的研究[J]. 力学学报，2010，42(3) ：343-349.

Xia Yuezhang，Zhu Keqin. A study of linear long wave attenuation over a Maxwell mud bed[J].Chinese Journal of Theoretical and Applied Mechanics，2010，42(3)：343-349(in Chinese).

Interaction Between Mud and Wave in Different Rheological Models

BAI Yu-chuan，TIAN Qi
(Institute of Sediment on River and Coast Engineering，School of Civil Engineering，Tianjin University，Tianjin 300072，China)

The theoretical model for wave propagation over muddy bottom was set up and solved, and the interaction between mud and wave—including mud transport and wave attenuation, was discussed.The velocity and pressure distribution of water and mud layers in different mud densities were calculated and analyzed, and the wave attenuation values in three different rheological models (viscous, power-law and viscoelastic models) were respectively calculated and compared with experimental data to analyze the affecting factors (mud thickness, wave period and water depth) of wave attenuation. The results show that the critical values of wave period and mud thickness exist, which can make wave attenuation the maximum. The wave attenuation rate decreases with increasing water depth. According to experimental results, the power-law fluid model is more suitable to describe the muddy bed.

estuary；mud；rheological model；wave attenuation

TV148

A

0493-2137(2011)03-0196-06

2010-06-10；

2010-09-26.

国家自然科学基金资助项目(40376028).

白玉川（1967— ），男，博士，教授.

白玉川，ychbai@tju.edu.cn.