利用最近邻域分类的图像去噪算法

宫霄霖，毛瑞全

（天津大学电子信息工程学院，天津 300072）

利用最近邻域分类的图像去噪算法

宫霄霖，毛瑞全

（天津大学电子信息工程学院，天津 300072）

为了在图像去噪的同时较好地保护图像细节，利用最近邻域的算法将数据进行有效的分类，得到了不同的有意义的封闭邻域，从而对突出的边缘细节信息与非边缘细节信息进行有效地分割，较好地改善了方形邻域固定、模糊边缘细节信息的问题.且利用小波分析之后的系数特征，估计出一个最佳阈值并进行阈值去噪.实验表明，该算法可以得到更好的实验结果.

图像去噪；脉冲耦合神经网络；图像分割；最近邻域

对图像进行去噪处理，是图像处理中的一项基础而重要的工作，对后续的工作如图像分割、特征分析以及模式识别等都有着重要的影响[1].

针对图像噪声中经常出现的高斯白噪声，利用小波变换进行处理已经成为主流方法[2-4].从阈值去噪[5]、相关性去噪，到现在诸多改进算法[6-7]，图像去噪的技术已经较为成熟[8].但是去噪过程中图像的边缘信息可能会被过度抑制，或者将相关性更强的邻域人为地破坏.在尽可能保持图像特征的情况下，进行去噪处理也是图像处理研究的重点之一[9].

笔者利用脉冲耦合神经网络[10]对图像进行了特征分析，粗略地进行了分类.为了提高计算速度，结合了最近邻域的思想进一步对已有的封闭邻域进行了分类.本文算法更有效地利用了小波系数的层内和层间相关性，从而更好地保护了边缘信息，恢复了原图像，即改善了去噪性能.

1 利用层内相关性的阈值去噪方法

对图像进行小波变换，对低频子带系数递归地使用低通和高通滤波器，意味着在一个小邻域内，处理后的图像系数是相关的，这个特性被称为层内相关性.也即在一个值较大的小波系数的邻域内，可能会有一组较大的小波系数；反之亦然[11].根据层内相关性的特点，一些阈值去噪方法被提出[12].

假设 dm,n是小波变换后的噪声图像系数.定义邻域窗口 Wm,n(d)包含所有落在以当前阈值化小波系数 dm,n为中心、边长为d的正方形内的小波系数.

对待阈值化的小波系数，用式(1)进行收缩[13]

式中：d,mn′为阈值后小波系数；收缩因子,mnα定义为

2 结合 PCNN图像分割的最近邻域分类去噪方法

2.1 脉冲耦合神经网络模型

脉冲耦合神经网络(pulse coupled neural networks，PCNN)[14]是根据猫等动物的大脑视觉皮层上的同步脉冲发放现象提出的一种新型神经网络，它是一种单层的、以迭代运算为主的神经网络.PCNN不需要提前训练，可自学习，因此广泛应用在图像处理中，包括图像融合[15]、图像分割、图像去噪[16]和图像目标识别等方面.

PCNN模型是由若干个神经元互连而构成的反馈型网络，每一个神经元 Nij都由接收部分、调制部分和脉冲产生部分 3部分组成(如图 1所示)[17].用PCNN对图像进行处理时，须将每个像素的灰度值作为每个神经元的输入.假设图像大小为AB×，因此AB×的图像矩阵对应AB×个PCNN神经元构成的神经元网络，且每个神经元Nij的活动可描述为[18]

式中：Sij、Uij和Yij分别为神经元 Nij的外部刺激(输入)、内部行为和输出；Lij、LV(NV)和Lα是神经元链接域的主要参数，分别为输入通道、放大系数和时间常数；与链接域参数相似，反馈域的参数也包括输入通道、放大系数和时间常数，分别为Fij、VF和αF；M和W分别为神经元之间的连接权系数矩阵；Tij和 VT是变阈值函数输出和阈值放大系数；αT为变阈值函数的时间常数；βij为连接权重.下标i、j表示像素的坐标，k、l表示神经元与周围连接的范围；n代表迭代次数.

图1 PCNN中单个神经元的模型Fig.1 Model of single neuron in PCNN

PCNN每个神经元通过将不同的输入值转化为不同的震荡频率，从而实现其对输入的量化.式(2)在仅考虑单个神经元，不受其他神经元相互影响的情况下，Lij、Uij和 Tij的表达式可简化为

式中：Fi代表单个神经元输入值，这里为图像像素灰度值；iL为链接输入；Ui为内部行为；VT为阈值放大系数；iV在有脉冲时为 VT，无脉冲时为零；下标i为得到的脉冲采样点，是不连续的离散值.

Tα和VT对阈值iT的变化有很大的影响，同时也直接影响到神经元的震荡频率.参数曲线U和T的交点是神经元震荡的点火点，此时满足

称式(7)和式(8)为 PCNN神经元的震荡特性方程.从两式可以看出，当Fi增大时，若保持αT不变，则i的采样点应更密集，这说明对于相同的参数αT，其震荡周期随像素的灰度值增大而减小，PCNN神经元的这种特性使得不同的像素输入产生不同的震荡频率，在各神经元不存在相互连接的情况下，像素灰度值输入值越大，点火频率越高，由此实现了对输入数据的量化.在图像处理中，PCNN实现了图像像素值到神经元点火频率的非线性映射.

当神经元之间通过W相互连接时，若周边神经元点火，由式(2)可知将导致当前神经元的U值最大，从而加速当前神经元的点火.W代表周边神经元输出对本神经元的贡献程度，本文算法根据图像像素点之间的冗余特性，采用了和中心点火点距离成反比关系的模板，此模板能达到强化边缘细节和平滑噪声的效果，其表达形式为

式中：x、y代表任意像素点所在的位置；i、j为当前着火点的位置.

2.2 结合PCNN图像分割的最近邻域去噪方法

利用 PCNN进行图像分割时，PCNN中每个神经元的输入对应为图像的每一个像素的灰度值.由于 PCNN模型所独有的神经元捕获特性，会使某一产生脉冲输出激发的像素引起附近其他类似灰度像素对应神经元的激发，相似的多个神经元就构成了一个神经元集群，该神经元集群同步地发放出脉冲.利用由 PCNN的脉冲传播特性所引发的同步脉冲发放，就可以按照图像自身性质将其分割成不同的封闭区域[19].

根据最近邻域的算法，将现有的分割后区域和待阈值点附近的固定窗口相互重叠，再次选择邻域范围.

假设 d,mn是当前待阈值的图像系数， dPCNNd为其所在的PCNN分割后的图像邻域，dwin为最近邻域方法提出的图像邻域，尺寸可为 5×5、7×7等，则根据本文算法， d,mn的邻域为

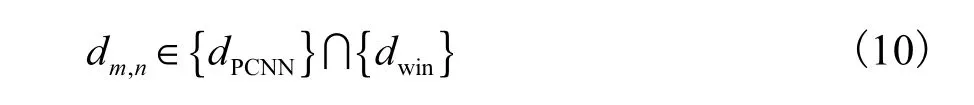
在图 2中，25点为待阈值点，虚线框为最近邻域，这里以5×5的窗口为例；细实线框为PCNN分割得到的邻域，可以看出 25点位于左上角的邻域内.根据式(10)，可得 10、16、17、18、23、24、25、32 点位于两个邻域重叠区域，从而构成了处理 25点所需要的邻域，图 2中用不规则形状标识出.其余的点由于不在最近邻域内或不在 PCNN分割的区域内而被去除.这里对算法复杂度进行分析，一个方形窗口需要 N2n2次处理，其中 N2为所加窗口的面积，n2为图像的像素点数目.而 PCNN分割后的图像邻域需要次处理，其中S为分割得到的邻域的数目，ni为第 i个邻域内的像素点数目，而=n2.所以PCNN图像分割的去噪方法需要次处理.故本文算法复杂度较方形窗口算法更高.

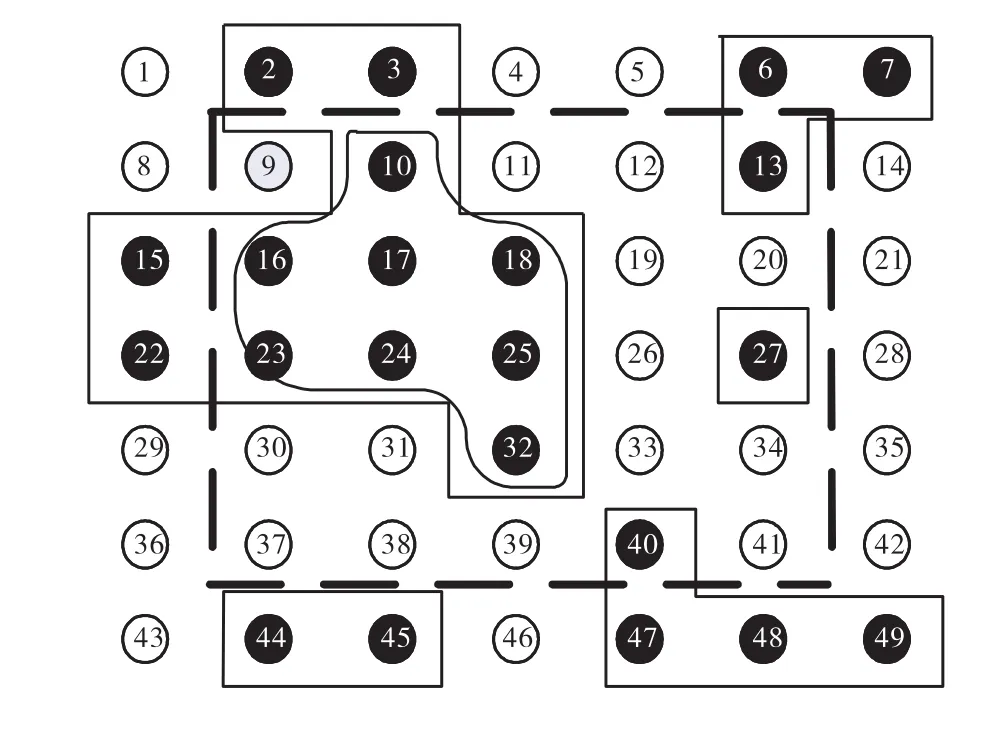
图2 改进的算法区域连接示意Fig.2 Regional connection of improved algorithm

3 本文算法实现

步骤 1将噪声图像 f(x，y)进行二维平稳小波变换，分别获得各个子带各层系数.

步骤2对第一层的低频系数利用PCNN进行图像分割.

步骤 3将低频系数保持不变，对各层的水平细节系数、垂直细节系数和对角细节系数分别进行贝叶斯软阈值算法邻域阈值处理.其中参与邻域阈值处理的邻域系数由式(10)得到的封闭区域决定(获取方法参见第2.2节).

步骤 4将低频系数和滤波后的高频子带进行平稳小波重构，即可得到去噪后图像ˆf.

4 实验结果与讨论

4.1 PCNN连接权系数矩阵大小讨论

连接权系数矩阵的大小会对图像分割结果产生较大的影响，较小或者较大均不能够得到接近图像自身信息的分割区域.因而要将图像分成性质相近的邻域，需要寻找一个合适大小的连接权系数矩阵来对图像进行处理.以下对连接权系数矩阵大小如何影响图像邻域分割进行讨论.

对图 3(a)利用不同的连接权系数矩阵边长进行分割，当边长为 8、13和18时，分割的结果分别如图3(b)、图 3(c)和图 3(d)所示.

图3 分割结果Fig.3 Segmentation results

从图 3的分割结果可以看出，图 3(b)中对图像分割区域较多，而这可能破坏图像本身的结构，造成过度分割.图 3(d)则将图像简单地分割成几个大的区域，没有遵循图像的自身信息；而图 3(c)较好地减轻了噪声的影响，并且分割结果较好地反映了图像自身信息.

利用 Canny算子对图 3(b)～(d)进行边缘检测，如图4所示，可以看出图4(c)的边缘信息保留最为完整.其中图 4(b)中存在大量的边缘信息，这是由于过度分割造成的；而图 4(d)没有检测到图片的主要信息，只分割成几个区域；图 4(c)大体遵循了图4(a)中的信息，得到的分割结果较好.本文中选择连接权矩阵边长为13.

图4 分割后边缘检测结果Fig.4 Edge detection with segmentation results

4.2 邻域内系数数目的讨论

本文算法阈值处理中使用的邻域系数是用PCNN分割后的邻域和固定方形窗口重叠得到的.然后利用贝叶斯软阈值算法进行阈值去噪.本实验对本文算法使用系数的情况进行了分析.

实验对 Lena.bmp图片进行了测试，加标准方差为15的噪声，采用sym8小波基，用平稳小波分解到3层，窗口大小为 3×3，表 1用于统计在 3×3窗口中出现的用于阈值处理的有效系数的个数.从表 1可以发现，在 3×3窗口中的系数全都用于阈值处理只有 17%，从而可以看出在 3×3窗口内存在大量不相关的系数，而用本文的方法可以有效地筛选相关性较强的系数，有效地避免了相关性较弱系数对于阈值处理时造成的影响.

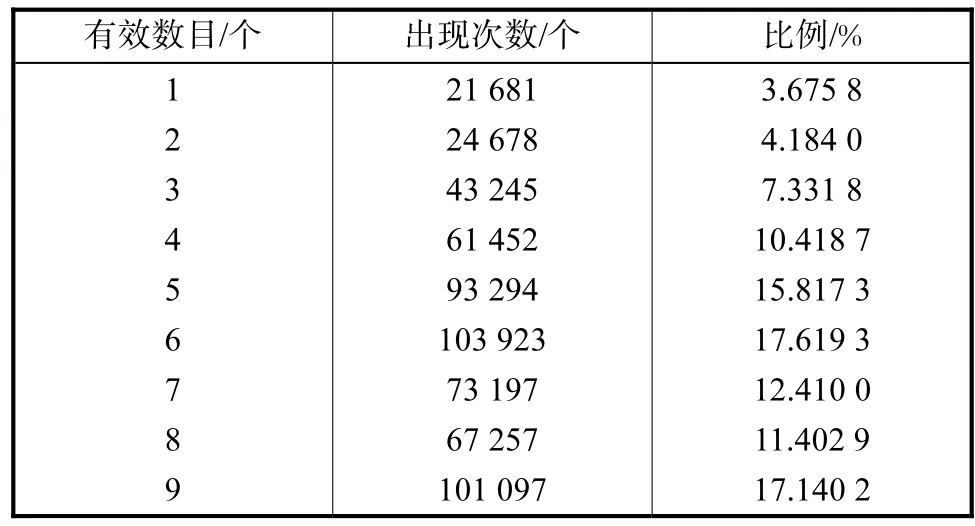
表1 统计窗口中出现的有效系数的个数Tab.1 Number of effective coefficents appearing in statistics window

4.3 不同噪声强度污染下本文算法的去噪效果讨论

对本文算法在不同强度噪声污染下的有效性进行讨论，实验中采用 Lena图片作为测试图片.噪声强度采用标准方差分别为10、15、20及25，小波分析中使用平稳小波分解到 3层，小波基采用 sym8.连接权系数矩阵边长这里采用 13，阈值采用常用的贝叶斯软阈值.这里采用 PSNR作为降噪性能优劣的衡量标准，实验结果参见表2.

表2 本文算法的去噪性能Tab.2 Denoising performances of proposed algorithm dB

从表 2给出的数据可以看出，使用本文提出的利用最近邻域分类的图像去噪算法可得到较高的峰值信噪比.相同情况下比方形窗口方法至少可高出约 2,dB，最多可高出约 5,dB.另外从视觉效果也可以看出本文算法优于方形窗口方法.如图5(c)～(e)为方形窗口方法在噪声标准方差为15下，利用不同窗口对加噪图像分别处理的结果，从图5中可以看出，该算法对噪声起到了一定的抑制，但是在平滑部分受到噪声影响仍然较明显，而且得到图像的边缘细节信息如人物头部帽子的纹理不够清晰；图5(f)～(h)是本文算法处理的结果，图像整体对噪声的抑制效果很好，平滑区域噪声的影响较小，且对于细节信息的保持也较方形窗口有了很好的提高，如帽子部分纹理清晰可见，整体上来看视觉效果更佳.

图5 Lena图像去噪效果Fig.5 Denoising results of Lena image

比较可看出，本文算法在很好地去除噪声的同时，也更好地保留了图像的边缘信息.另外，因为平稳小波在抽样后进行了插值操作，故较好地保持了相位不变性，使得小波的层内相关性保持得更好.因此本文方法可以得到更高的PSNR.

5 结 语

在深入研究了各种小波去噪算法及 PCNN在图像分割中的应用后，针对使用方形窗口去噪处理会将边缘信息过平滑，以及不能自适应地将与阈值处系数相似的系数一起处理的缺点，提出了利用PCNN进行图像分割.根据图像自身的性质，将图像划分成为各个不规则的邻域.然后根据小波的层内相关性原理，使用最近邻域的思想对各个分割的区域加以限制，从而更加遵循了图像自身的特点，较好地保留了边缘细节信息.

通过与方形固定邻域算法在不同情况下去噪效果的比较，可以清楚地看到，本文算法可以更好地去除噪声，保留边缘.

［1］Kivanc M M， Kozintsev I，Ramchandran K，et al. Lowcomplexity image denoising based on statistical modeling of wavelet coefficients[J].IEEE Signal Processing Letters，1999，6(12)：300-303.

［2］Donoho D L，Johnstone J M. Ideal spatial adaptation by wavelet shrinkage[J].Biometrika，1994，81(3)：425-455.

［3］Donoho D L，Johnstone J M. Wavelet shrinkage：Asymptopia[J].Journal of the Royal Statistical Society，1995，57(2)：301-369.

［4］Coifman R R，Donoho D L. Translation-invariant denoising[J].Springer Lecture Notes in Statistics，1995，103：125-150.

［5］Cai T T，Silverman B W. Incorporating information on neighbouring coefficients into wavelet estimation[J].The Indian Journal of Statistics，2001，63：127-148.

［6］宫霄霖，毛瑞全，刘开华. 基于自适应邻域系数的小波图像阈值降噪[J]. 计算机工程，2010，36(11)：206-208.Gong Xiaolin，Mao Ruiquan，Liu Kaihua. Images denoising based on adaptive neighboring coefficients in wavelet domain[J].Computer Engineering，2010，36(11)：206-208(in Chinese).

［7］Ma Yide，Tian Yong，Zhang Jiuwen. Wavelet-domain image denoising using contextual hidden Markov tree model[C]//2007IEEE International Conference on Automation and Logistics. Jinan，China，2007：2617-2621.

［8］宫霄霖，毛瑞全，刘开华. 基于边缘检测的邻域加窗图像去噪算法[J]. 光电工程，2009，36(11)：112-117.

Gong Xiaolin，Mao Ruiquan，Liu Kaihua. Image denoising algorithm based on edge detection with neighborhood weighed window[J]. Opto-Electronic Engineering，2009，36(11)：112-117(in Chinese).

［9］Zhou Zuofeng，Cao Jianzhong，Liu Weihua. Contourletbased image denoising algorithm using adaptive windows[C]//2009 4thIEEE Conference on Industrial Electronics and Applications. Xi'an，China，2009：3654-3657.

［10］Johnson J L，Padgett M L. PCNN models and applications[J].IEEE Transactions on Neural Networks，1999，10(3)：480-498.

［11］Eom Il Kyu，Kim Yoo Shin. Wavelet-based denoising with nearly arbitrarily shaped windows[J].IEEE Signal Processing Letters，2004，11(12)：937-940.

［12］Chen G Y，Bui T D，Krzyzak A. Image denoising with neighbour dependency and customized wavelet and threshold[J]. Pattern Recognition，2005，38(1)：115-124.

［13］Chen G Y，Bui T D，Krzyzak A. Image denoising using neighbouring wavelet coefficients[J].Image Denoising Using Neighbouring Wavelet Coefficients，2005，12(1)：99-107.

［14］Zhou Liang，Zheng Jianguo. A new approach for color image edge detection using improved PCNN[C]//WSEASInternational Conference on Simulation，Modelling and Optimization. Beijing，China，2007：6-11.

［15］Yang Shuyuan，Wang Min，Lu Yanxiong，et al. Fusion of multiparametric SAR images based on SW-nonsubsampled contourlet and PCNN[J].Signal Processing，2009，89(12)：2596-2608.

［16］Zhang Hongjuan，Zhang Zongnian，Lin Dongmei，et al. A novel image de-noising algorithm combined PCNN with morphology[C]//2007International Symposium on Intelligent Signal Processing and Communication Systems.Xiamen，China，2007：208-211.

［17］Duan Lijuan，Lin Zhiqiang，Miao Jun，et al. A method of human skin region detection based on PCNN[C]//Advances in Neural Networks. Wuhan，China，2009：486-493.

［18］Tu Yongqiu，Li Shaofa，Wang Minqin. Mixed-noise removal for color images using modified PCNN model[C]//2008International Symposium on Intelligent Information Technology Application.Shanghai，China，2008：347-351.

［19］Kurokawa H，Kaneko S，Yonekawa M. A color image segmentation using inhibitory connected pulse coupled neural network[C]//International Conference on Neural Information Processing. Auckland，New Zealand，2008：776-783.

Image Denoising Algorithm Using Nearest-Neighborhood Classification

GONG Xiao-lin，MAO Rui-quan
（School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China）

To keep image details during image denoising, an effective algorithm was proposed to classify the data based on nearest-neighborhood method so as to get various close domains. In this way the salient edge and non-edge information can be divided effectively. This proposed method can improve the original method, which may blur the edge. An optimum threshold was estimated to de-noise the degraded image. The experiments show that the scheme can get better result than others.

image denoising；pulse coupled neural networks；image segmentation；nearest neighborhood

TN391

A

0493-2137(2011)03-0266-06

2009-09-04；

2009-11-13.

宫霄霖（1981— ），女，博士，讲师.

宫霄霖，gxl@tju.edu.cn.

book=2011,ebook=239