水轮发电机多物理场综合优化设计

朱殿华，郭 伟

(天津大学机械工程学院，天津 300072)

水轮发电机多物理场综合优化设计

朱殿华，郭 伟

(天津大学机械工程学院，天津 300072)

以水轮发电机为典型复杂产品研究实例，深入分析了电机稳态工作时多物理场的相互耦合作用，对电机的电磁场、通风散热流-固热耦合场进行了数值分析和计算，计算结果切实有效.在此基础上，从系统的角度出发，通过对电机设计过程中电磁、通风、散热学科进行分析，确立了学科间的参数耦合关系，建立了电机综合优化设计模型，采用集成优化方法 MDF对此模型进行了优化求解，优化后的设计方案通过数值计算进行了有效验证，初步实现了电机综合优化设计，进而为多领域复杂产品的综合优化做出了有益探索.

水轮发电机；耦合；综合优化；自动化

复杂产品诸如飞机、汽车、掘进机等大型产品的设计过程具有设计变量和约束数目多、领域间耦合关系复杂、设计过程繁琐且难以实现设计结果的优化和缺乏有效的方案验证手段等特点和难点.当前学术界的研究热点多集中于复杂产品的建模、集成分析技术、多学科优化技术实现等方面[1-10]，可付诸实践的工程研究成果鲜有发表.笔者以水轮发电机为研究对象，针对电机设计过程复杂、工作过程中存在的多领域耦合现象进行深入分析，力求实现电机设计过程的自动化和综合优化.

1 多物理场数值分析方法

1.1 电磁场数值计算

选用立式水轮发电机为分析模型，该电机定子108槽，转子4对磁极.具体参数为：视在功率11,764.7,kVA，额定电压 6,300,V，功率因数 0.85，工作频率50,Hz，励磁电流1,078.2,A.

电机中的电磁场问题一般归结为一个偏微分方程的边值问题[11].为了简化磁场计算，这里不考虑电机端部效应，认为磁场在轴向方向上是均匀分布的，因此利用二维静态电磁场来进行分析和计算.为了考虑电机的转子磁极、定子齿槽、气隙大小以及铁磁材料对电机电磁场的影响，选取整个电机圆周为计算区域，以矢量磁位Az作为求解变量.现对电机做出假设：

(1) 采用二维电磁场计算，选取国际单位制；

(2) 不考虑交变磁场在定子绕组、铁心冲片及机座中的涡流反应，因此同步发电机的磁场可作为非线性稳定磁场来处理；

(3) 铁心里的磁导率是各向同性的.

在上述假设前提下，得到非线性泊松方程和边界条件为.

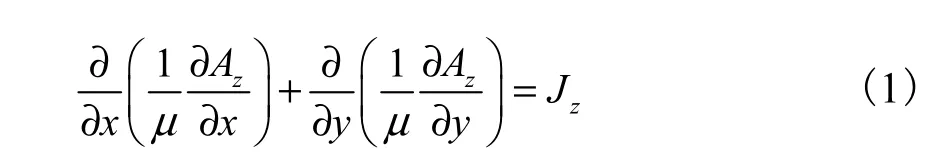
求解区域 Ω：整个剖分区域边界条件为定子外圆边界 Bn=0.

采用 ANSYS软件的电磁分析部分对电机的空载磁场进行数值计算.单元类型采用 PLANE53 八节点四边形/六节点三角形的二维单元对实体模型进行剖分，得到电机二维模型以及剖分后图形如图1所示.

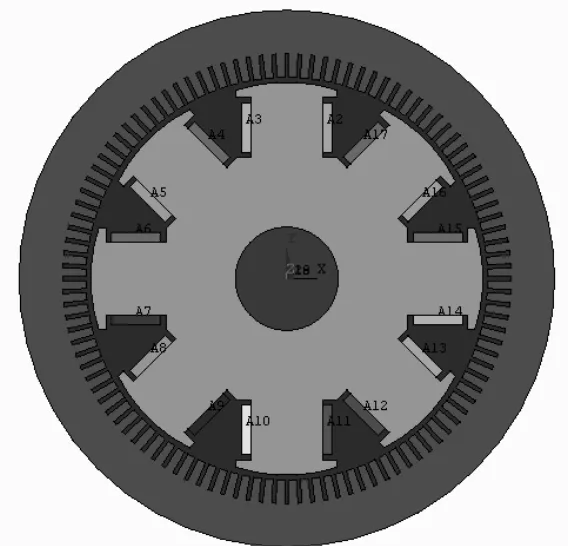
图1 电机二维几何模型Fig.1 Two-dimensional geometric model of generator

通过 ANSYS后处理可以得到空载时的路径点磁位曲线，如图2所示.

根据路径点磁位曲线可以进行气隙磁场和空载特性的计算.计算得空载电势 Ev= 6 301.355823V ，与设计值6,300,V基本吻合.从而证明了电磁场数值计算的有效性.

图2 路径点磁位曲线Fig.2 Magnetic potential curve of path point

1.2 流-固热耦合场数值分析

电机运行过程中，电磁场、流场和温度场同时存在.因此，从热耦合的角度进行通风、散热系统的数值计算更具有工程价值.

图3 电机通风系统示意Fig.3 Ventilation system diagram of generator

实验模拟立式水轮发电机电机部分的流-固热耦合场，采用的是径向自通风冷却系统如图 3所示.由冷却器出来的冷却空气在挡风板的限制下，流经转子支架，转而向外经过转子磁轭径向通风孔、磁极间隙、定转子间隙和定子径向通风槽片间隙，对转子线圈、定子线圈和定子铁芯等部件进行冷却后流回空气冷却器，冷却后的空气重新进入风道进行冷却.在流动过程中，冷却空气会和定、转子的升温部件发生对流换热，主要发生在以下几个部分.

(1) 在流过定、转子间隙过程中，冷却空气会和定子齿表面、定子线圈外部包裹物和转子铁芯上表面发生对流换热.

(2) 在流经转子磁极间隙的过程中，会和转子线圈的迎风面发生对流换热.

(3) 在流过定子径向通风槽片间隙的过程中，会和定子铁芯以及定子线圈外部的云母带发生对流换热.

立式水轮发电机定子温度场的热源有定子铁芯和定子线圈.其产生的损耗主要包括：额定电流时定子绕组的基本铜耗，额定电流时定子绕组的附加铜耗，空载额定电压时定子轭中的铁耗等，热损耗值可通过电磁计算过程获得.立式水轮发电机的转子热损耗包括励磁绕组中的铜耗和分布在转子磁极表面及阻尼绕组中的附加损耗.其热损耗值同样可通过电磁计算过程获得.

电机工作时，强制通入的空气介质与固体之间、固体与固体之间将产生对流换热和导热过程，其原理主要是传热学中的传热基本定律[12].

在热力学第一定律基础上，结合傅里叶定律，获得温度场数学表达式，再得到导热微分方程.推导出的笛卡尔坐标系下三维非稳态导热微分方程的一般形式为

式中：(x ,y,z)为导热物体中的任意点坐标，在该点分割出一个平行六面体微元dV；Φ˙为单位体积发热率；ρ、cp、τ分别为微元体的密度、比定压热容和时间.

对于对流换热，用数学方法解决时要求解包括3种情况的方程组，质量的连续性方程、动量的运动方程和能量守恒方程[13]分别为

式中：pc为比定压热容，J/(kg·K)；ρ为密度，kg/m3；λ为导热系数，W/(m·K).上述 3个方程是采用FLUENT软件进行三维数值模拟的理论依据.

鉴于分析对象立式水轮发电机在结构上的对称性和各个物理场的周期性分布，并且转子支架有7个支架孔，为了提高计算速度，建立 1/28模型进行分析.由于模型的复杂性，为了保证计算的可行性，在保证计算准确性的前提下对流场和两个温度场求解区域的结构上做出假设.

(1) 所要求解的是定、转子温度场，因此流场的求解区域取电机转子支架进口处到定子轭出口处，建立计算模型.

(2) 定子入口和出口处均有定子线圈，虽然此处结构复杂，数量巨多，但是对气流影响有限.如果考虑，结构将十分复杂，网格数量将十分巨大，普通计算机无法计算，而且数值解可能是发散的.为简化计算先不考虑定子槽外线圈影响.

(3) 转子是静止的，计算时只考虑稳态运行时情况.

(4) 两个定子齿中间的定子线圈为发热热源，简化为中部线圈，忽略掉包裹它们的绝缘体.

(5) 因为线圈棒槽部铜与端部铜之间的热交换可以忽略，建模时不考虑端部线圈.

(6) 假设定子铁心与线圈棒紧密相连.

(7) 转子的励磁绕组(转子线圈)结构简化为长方体结构.由于励磁绕组的铜线采用七边形结构，其外边为 1个三角形，如近似为一平面，这样减小了线圈和磁极间隙空气的接触面积，从而减少了散热面积，减少了对流换热量，实际上增大了安全系数.

(8) 转子端部主要由励磁绕组、压板以及引线等组成，其端部及极间通风损耗(摩擦损耗)可认为很小不加考虑.

(9) 励磁绕组的绝缘比较复杂，绕组匝间绝缘最厚为0.3,mm，故假定绕组之间不存在绝缘.

根据以上的条件及假设，建立水轮发电机的流场和温度场的求解区域模型，如图4所示.

图4 通风、散热系统几何建模Fig.4 Geometric model of ventilation and cooling system

将上述模型带入 CFD旗舰产品 FLUENT进行流-固热耦合数值计算，分析结果如图5所示.

图5 流场速度矢量Fig.5 Velocity vectors of flow field

由图 5可以看出转子轭径向通风孔中空气的流速最大，平均流速在32.8～37.4,m/s.符合流量一定的条件下，过流面积越小，流速越大的基本原理.

由图 6可以看出磁极与转子线圈接触的部位温度最高，因为这个部位属于热量集聚部位，散热路径较长，热量较难散走.由图 7可以看出由于某些流线在转子轭径向通风口较窄，故许多流线在此处折回.在其他条件允许下尽可能增大其面积可以有效改善通风状况.

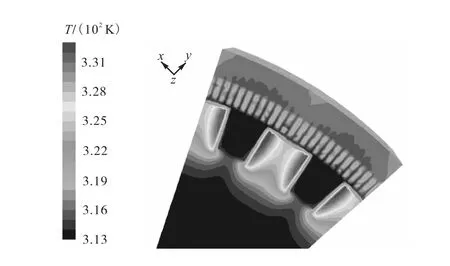
图6 电机温度场分布Fig.6 Temperature field distribution of generator

图7 流场迹线Fig.7 Particle pathlines of flow field

通过数值计算可以观察到电机运行过程中各关键点的工况，但由于数值计算比较费时，而且对初始参数的依赖性较大，通用性较差，所以更适合做方案设计优化后的验证手段.

2 综合优化设计

水轮发电机方案设计属典型多领域耦合设计问题.具体表现在：电磁学科、通风计算和热分析过程中，彼此之间存在着诸多学科间交叉变量；传统的、串行的基于单一学科分析的发电机方案设计流程割裂了电磁、通风、热计算等学科间固有的耦合关系.其直接结果会导致即使某一学科取得最优值，却不能保证整个电机方案设计结果最优，从而因不能充分发挥电机材料的使用性能而导致电机加工、制造成本的增加.因此，若要从系统的角度出发，得到整个发电机系统的综合优化解，就必须根据学科间参数耦合关系，建立起综合优化数学模型，对电机进行多学科协同优化设计，实现电机综合利用性能的最大化.

2.1 综合优化模型的建立

通过深入分析电机的方案设计过程，可将电机的设计问题划分为电磁、通风、热计算3个子学科，学科间耦合关系如图8所示.

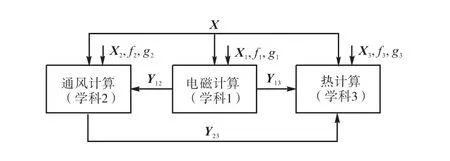
图8 电机综合优化模型Fig.8 Integrated optimization model of generator

电机综合优化设计模型中，各变量含义为

X为设计需求向量，包括视在功率、额定电压、转速、功率因数和额定频率5个基本参数.

X1为电磁学科设计向量，包括定子、转子、励磁、电流、阻尼、损耗和判定系数 7个方面共 81个设计参数.

X2为通风学科设计向量，包括定子通风槽、磁轭风隙、冷却器和空气温度等4个方面共16个参数.

X3为热计算学科设计向量，本例只包括设计需求向量.

g1、f1分别为电磁学科各变量的约束条件和目标函数.

g2、f2分别为通风计算学科各变量的约束条件和目标函数.

g3、f3分别为热计算学科各变量的约束条件和目标函数.

Y13为电磁计算后输入热计算学科的状态向量.所包含的状态变量包括定子轭、定子齿、齿-轭之间沿径向热阻、端部线圈和绝缘热阻 5方面共 10个耦合状态变量.

Y23为通风计算后输入热计算学科的状态向量.主要指流经定子径向风沟、定子轭通风隙处的风速.

Y12为电磁计算后输入通风计算学科的状态向量.包括定子外径、定子通风沟结构尺寸、转子支架外径、极靴尺寸和轴承损耗等共7个耦合状态变量.

2.2 寻优策略的选择和制定

电机方案设计过程中，电磁学科与通风、热计算学科间不但存在着大量共享设计变量，还存在着相当数量的耦合状态变量，其中电磁设计过程最复杂，多学科优化过程中难以进行包括 GSE在内的全局灵敏度分析[14].考虑到3个学科设计变量数较少(低于700个)，故在寻优策略的选择上采用了单级优化算法中的MDF形式，如图9所示.该算法易于构造，无需计算全局灵敏度分析，且优化过程中涉及的学科数目不大，具备可行性.

采用 MDF寻优策略，确立电机系统级多学科优化目标为：电机电磁性能最优的前提下，尽量降低整机最大风速值和定子最高温升.全局优化的数学模型及各变量含义参见式(6)和表1.

图9 电机MDF寻优策略Fig.9 Generator′s MDF formulation

表1 电机综合优化设计变量Tab.1 Variables for integrated optimization design of generator

2.3 优化过程及实现

针对上述 MDF算法构造形式，在多学科优化集成软件 ISIGHT[15]中搭建计算框架，寻优算法采用多目标改进遗传算法 NSGA-Ⅱ法进行求解.设定种群大小为 100，进化代数为 200，杂交率为 0.9，进化至100代时算法收敛.优化后得到改善的电机总体性能指标值列于表2.

图10给出了综合寻优后得到的电机空载特性曲线.可以看出：电机的空载特性得到显著改善，因而磁场分布更为合理，电磁方案设计结果更为有效.采用优化后的设计参数值进行电机内流-固热耦合场数值计算可知：流-固热耦合场的变化较小.具体体现在：优化后电机内的风量和风压分配仍能满足通风需求(yu0P ＞ )；调整后的通风散热条件下，定子最高温度为 369,K(93,℃)，比优化前温度降低了 3,℃.由此可见，经过综合优化设计，热源处的温升现象亦能得到改善，从而提高了电机的使用寿命.

表2 总体性能目标值对比Tab.2 Comparison of overall performance index

图10 电机优化前后的空载特性Fig.10 Comparison of no-load characteristic between Fig.10 generator with and without optimization

3 结 语

采用数值计算方法先后对水轮发电机工作时的电磁场、流场和温度场进行了数值计算和分析，建模手段和模型假设条件符合工程实际，应用实例证明了数值计算方法的有效性.在此基础上，借鉴多学科优化思想，对电机的典型设计过程进行分析，建立了学科间耦合的综合优化设计模型，并采用了有效的寻优策略进行了模型求解.求解后得到的参数化设计方案可通过数值计算进行验证，全面提升了水轮发电机的设计质量和效率，为电机的综合优化设计探明了方向，进而为实现复杂产品多领域综合优化设计打下了良好基础.

［1］Suh N P. Axiomatic design theory for system[J].Research in Engineering Design，1998，10(4)：189-209.

［2］Xu Yong，Zou Huijun. Research on conceptual design of mechatronic systems[J].Conceptual Design of Mechatronic Systems, 2006，31(6)：661-669.

［3］Borges R，Mota A. Integrating UML and formal methods[J].Electronic Notes in Theoretical Computer Science，2007，184：97-112.

［4］Shirwaiker Rohan A，Okudan Gül E. Triz and axiomatic design：A review of case-studies and a proposed synergistic use[J].Journal of Intelligent Manufacturing，2008，19(1)：33-47.

［5］Sobieszczanski-Sobieski. Multidisciplinary aerospace design optimization：Survey of recent developments[J].Structural Optimization，1997，14(1)：1-23.

［6］李伯虎，柴旭东. 复杂产品虚拟样机工程[J]. 计算机集成制造系统-CIMS，2002，8(9)：678-683.

Li Bohu，Chai Xudong. Virtual prototyping engineering for complex product[J].Computer Integrated Manufacturing Systems，2002，8(9)：678-683(in Chinese).

［7］刘 静，潘双夏，冯培恩. 挖掘机器人虚拟样机建模策略与仿真技术研究[J]. 浙江大学学报，2004，38(11)：1490-1495.

Liu Jing，Pan Shuangxia，Feng Peien. Modeling and simulation of virtual robotic excavator prototype[J].Journal of Zhejiang University，2004，38(11)：1490-1495(in Chinese).

［8］Alexandra Schönning，Jarnal Nayfch，Richard Zarda. An integrated design and optimization environment for industrial large scaled systems[J].Research in Engineering Design，2005，16(2)：86-95.

［9］Qian Z，Xue C，Pan S. FEA agent for multidisciplinary optimization[J].Structural and Multidisciplinary Optimization，2001，22(5)：373-383.

［10］Jang B-S，Yang Y-S，Jung H-S，et al. Managing approximation models in collaborative optimization[J].Structural and Multidisciplinary Optimization，2005，30(1)：11-26.

［11］璆汤蕴 . 电机内的电磁场[M]. 2版. 北京：科学出版社，1998.

Tang Yunqiu.Electromagnetic Field Within the Motor[M]. 2nd ed. Beijing：Science Press，1998(in Chinese).

［12］杨世铭，陶文铨. 传热学[M]. 北京：高等教育出版社，2003.

Yang Shiming，Tao Wenquan.Heat Transfer[M].Beijing：Higher Education Press，2003(in Chinese).

［13］王福军. 计算流体动力学分析[M]. 北京：清华大学出版社，2004.

Wang Fujun.Computational Fluid Dynamics[M]. Beijing：Tsinghua University Press，2004(in Chinese).

［14］Yi S I，Shin J K，Park G J. Comparison of MDO methods with mathematical examples[J].Structural and Multidisciplinary Optimization，2008，35(5)：391-402.

［15］Hong U P，Hwang K H，Park G J. A comparative study of software systems from the optimization viewpoint[J].Structural and Multidisciplinary Optimization，2004，27(6)：460-468.

Integrated Optimization Design of Hydro Generator Based on Multi-Physics Field

ZHU Dian-hua，GUO Wei
(School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)

As a representative complex product, a number of coupling relationships exist among hydro generator’s electromagnetic field (EMF), flow field and temperature field when it works. In this paper, these complicated coupling interactions were thoroughly analyzed and numerical analysis and calculations for EMF, solid-fluid thermally coupled fields were executed effectively. On this basis an integrated optimization model was formed through carrying out such disciplinary analysis as electromagnetic design, ventilation and cooling design sequentially and then identifying interdisciplinary coupling parameters. In the end MDF formulation was adopted to get optimized parameter values to formulate a new design. This new design is tested by numerical simulations. This practice is a good approach for realizing a good comprehensive design of hydro generator and other complex products.

hydro generator；coupling；integrated optimization；automation

TH122

A

0493-2137(2011)03-0277-06

2009-12-02；

2010-07-05.

国家自然科学基金资助项目(50875183).

朱殿华（1975— ），女，博士，讲师，zdhme@126.com.

郭 伟，教授，wguo@tju.edu.cn.