基于矢量泰勒级数的鲁棒语音识别

吕 勇，吴镇扬

(东南大学信息科学与工程学院，南京 210096)

基于矢量泰勒级数的鲁棒语音识别

吕 勇，吴镇扬

(东南大学信息科学与工程学院，南京 210096)

矢量泰勒级数是一种有效的抗噪声鲁棒语音识别算法.然而在对数谱域，美尔滤波器组的不同通道之间有较强的相关性，因而难以从含噪语音中准确估计噪声的方差.提出了一种基于矢量泰勒级数的倒谱域特征补偿算法.该算法在倒谱域，用一个高斯混合模型描述语音倒谱特征的分布，通过矢量泰勒级数从含噪语音中估计噪声的均值和方差.实验结果表明，此算法能明显提高语音识别系统的性能，优于基于矢量泰勒级数的对数谱域特征补偿算法.

特征补偿；矢量泰勒级数；噪声估计；鲁棒语音识别

在实际应用中，由于训练环境和测试环境的失配，语音识别系统的性能可能会急剧恶化.通常可以从特征域[1-6]和模型域[7-8]2个方面减小环境失配对语音识别系统的影响.特征域方法对语音特征进行归整，提取抗噪能力强的特征参数[1]或对噪声环境下提取的特征向量进行补偿，尽可能将其恢复成纯净语音特征向量[2-6].模型域方法根据测试环境下的少量自适应数据[7]或静音段得到的噪声信息[8]，调整声学模型的参数，使之与测试环境下的特征向量相匹配.

相对于模型域方法，特征补偿具有计算量小，处理时变噪声能力强的优点，因此在噪声补偿中得到了广泛应用.基于模型的特征补偿算法最初由Erell等[2]和 Acero[3]提出，在训练阶段，用一个高斯混合模型(Gaussian mixture model，GMM)描述纯净语音特征的分布；在识别阶段，首先根据噪声参数调整 GMM的均值和方差，使之与测试环境匹配，然后根据含噪特征向量的后验概率，用最小均方误差(minimum mean squared error，MMSE)方法估计纯净语音的特征参数.为了从含噪语音中获得噪声参数的闭式解，Moreno等[9-10]在对数谱域用矢量泰勒级数(vector Taylor series，VTS)逼近纯净语音与含噪语音之间的非线性关系.然而，在对数谱域，美尔滤波器组的不同通道之间有较强的相关性，因而噪声协方差矩阵的非对角元素较大，难以忽略.而且，尽管已经用一阶VTS近似非线性失配函数，辅助函数关于噪声方差的导数仍然是非线性的，没有闭式解.因此，Moreno[10]仅估计噪声的均值，在估计含噪语音GMM的方差时忽略噪声的方差.这不仅会带来误差，而且有可能导致矩阵奇异.Kim 等[11]提出了一种基于逐帧(frameby-frame)噪声估计的 VTS方法，对 GMM 的每个高斯单元分别估计噪声的均值和方差，再加权平均，得到最终的噪声参数.逐帧噪声估计的计算量非常大，大约是批处理(Batch)噪声估计[10]的 N倍(N为当前单词发音的帧数)[12].且逐帧噪声估计的结果不如批处理噪声估计准确[12].因此在 VTS算法中噪声一般都用批处理方式估计[13-14]，即对每个单词发音，合并所有高斯单元的全部数据，估计同一组噪声参数(均值和方差).在文献[13-14]中，噪声的方差通过牛顿法估计，即在每次迭代中将辅助函数的导数近似为线性函数.牛顿法不仅需要较多的迭代次数(相对于闭式解)，而且因为要计算辅助函数的二阶偏导数，计算量很大，不利于系统的实时实现.

笔者提出了一种基于矢量泰勒级数的倒谱域特征补偿算法.该算法在倒谱域，用一个高斯混合模型描述语音倒谱特征的分布，通过矢量泰勒级数方法从含噪语音中估计噪声的均值和方差.该算法不仅调整GMM的均值向量，而且从含噪语音中估计加性噪声的方差，从而更新GMM的协方差矩阵.在倒谱域，特征向量不同维数之间的相关性较小，因而可以将语音模型和噪声模型的方差近似为对角矩阵.根据这一假设，本文采用基于期望最大(expectation-maximization，EM)算法[15]的噪声方差估计方法.该算法可以看成是对数谱域VTS特征补偿算法[10]的一种推广.

1 倒谱域矢量泰勒级数关系

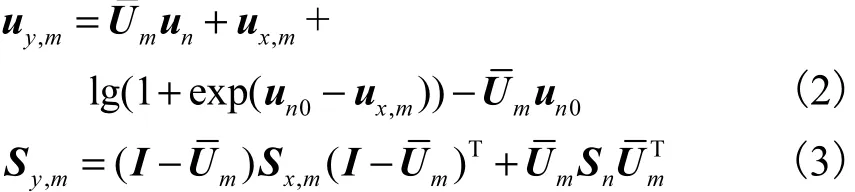
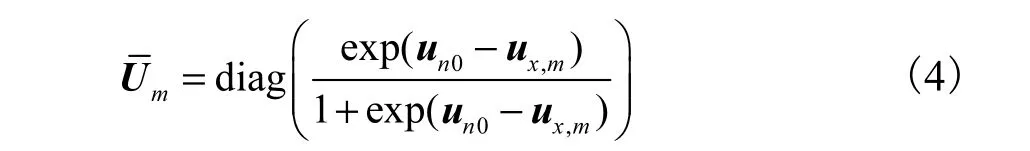
式中：ux,m和 Sx,m分别表示纯净语音GMM第m个高斯单元的均值向量和协方差矩阵；un和 Sn分别表示加性噪声的均值和方差；un0是 un上一次迭代得到的初值；I表示单位矩阵；diag( )表示以括号中的向量为对角元素，生成对角矩阵.文献[10]只考虑噪声的均值 un，忽略了方差 Sn.因而，含噪语音协方差矩阵 Sy,m仅仅通过式(3)右边第 1项估计.当接近单位矩阵I时，忽略第 2项，有可能导致矩阵奇异.

直接在倒谱域估计纯净语音特征参数，用一个GMM描述纯净语音倒谱特征x的分布

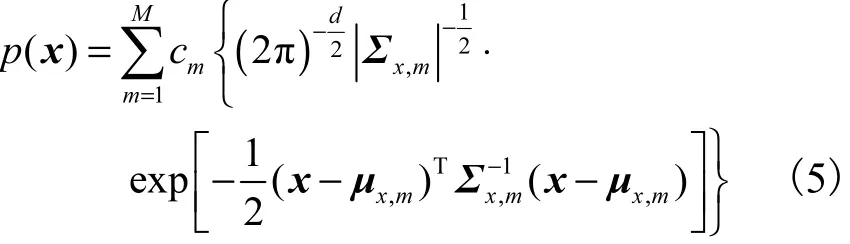
式中：cm、µx,m和Σx,m分别表示第m个高斯单元的混合系数、均值向量和协方差矩阵；d表示倒谱特征的维数；M表示混合数.

通过离散余弦变换(discrete cosine transform，DCT)，将式(1)变换到倒谱域，即

在式(3)两边同时左乘DCT矩阵C，右乘C的转置矩阵TC ，可得

通常假设噪声只影响GMM的均值和方差，不影响混合系数.在用式(7)和式(10)更新 GMM 的均值和方差前，必须先估计未知参数μn和Σn.

2 噪声参数估计

噪声参数µn和Σn通过EM算法[15]和最大似然准则，从含噪语音中估计.EM算法的辅助函数定义为

式(19)表示对当前帧的前K帧和后K帧进行差分，K为常数，本文设置为4.

3 实验结果及分析

用 TIMIT语音库评估所提算法的性能.该语音库中的两句对话被拆分为21个单词，用于孤立词语音识别.训练集包括144个说话人，共3,024个单词样本；测试集包括71个说话人，共1,491个单词样本.测试样本在不同信噪比下与噪声混合产生测试数据..3种噪声，White、Pink与Factory，来自NOISEX-92 噪声库.

TIMIT的 16,kHz语音，通过低通滤波器降采样到 8,kHz.在美尔频域，将位于 64,Hz～4,kHz的有效频带分为 20个等宽通道.每帧数据长 16,ms，帧移为8,ms.每帧的特征向量包括13个倒谱系数(包括0阶系数)及其一阶差分系数.每个单词用一个 6状态左右结构隐马尔可夫模型(hidden Markov model，HMM)建模，每个状态有 4个高斯单元.用于特征补偿的倒谱域GMM和对数谱域GMM均包括400个高斯单元.HMM和GMM高斯单元的方差均设为对角矩阵.在 EM 算法的第 1次迭代中，噪声的初始均值µ0n和初始方差Σ0n(对应σ0n)分别设置为零向量和单位矩阵.

表 1是 3种噪声(White、Pink和 Factory)环境下，不同信噪比时原 VTS算法[5]和本文算法的误识率.本文算法包括算法 1和算法 2，算法 1只更新GMM 的均值；算法 2同时更新均值和方差.从表 1可以看出，本文算法 1优于原 VTS算法.这是因为，倒谱域 GMM 和对数谱域 GMM 均用对角协方差矩阵，以减小计算量；而倒谱系数之间的相关性比对数谱系数小得多，因此在倒谱域，用对角协方差矩阵代替满矩阵描述语音特征的分布，导致的误差更小.

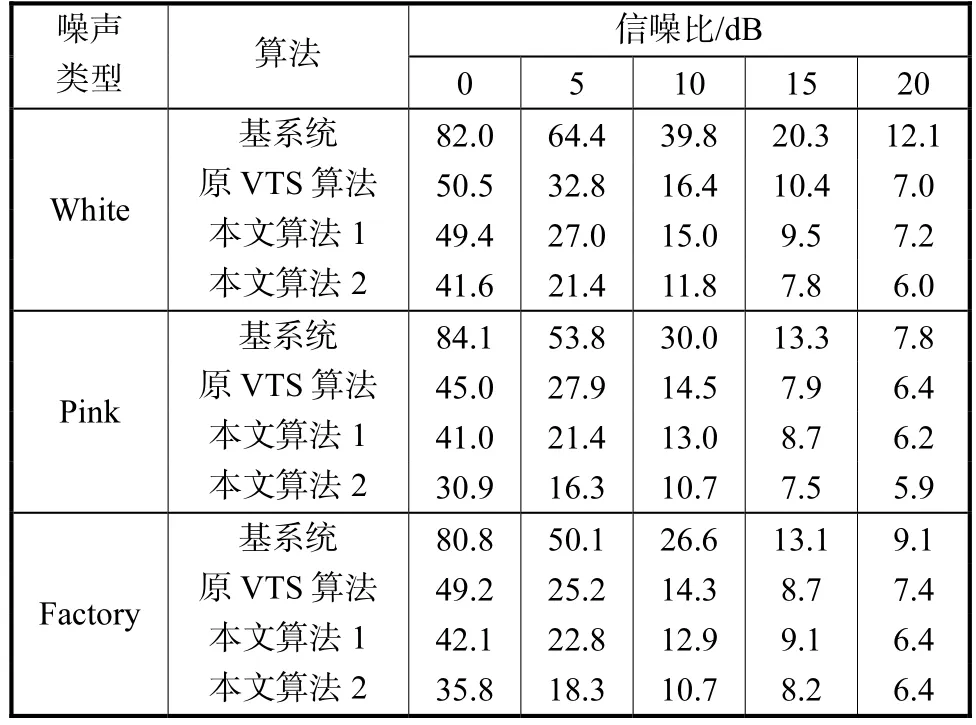
表1 3种噪声环境下不同信噪比时的误识率Tab.1 Word error rates with different signal-to-noise ratios for three types of testing noise %

表 1同时表明，相对于本文算法 1，本文算法 2有更低的单词误识率，尤其在低信噪比时，性能提高更为明显.这充分说明了本文提出的方差自适应算法的有效性.比如，0,dB时，White、Pink和 Factory噪声环境下，本文算法 2相对于本文算法 1，识别率分别提高了 7.8%、10.1%和 6.3%.式(8)表明，信噪比越低，含噪语音协方差矩阵与纯净语音协方差矩阵之间的偏差就越大.因此，低信噪比时，有必要调整GMM的协方差矩阵.

图 1为不同信噪比时，原 VTS算法和本文算法在3种噪声(White，Pink和 Factory)环境下的平均误识率.由图1可知，在各种信噪比环境下，本文算法2的平均误识率最低.在 0,dB、5,dB、10,dB、15,dB 和20,dB信噪比环境下，本文算法 2相对于原 VTS算法，绝对误识率分别下降了12.1%、9.9%、4.0%、1.1%和0.8%，相对误识率分别下降了25.1%、34.8%、26.5%、12.9%和12.0%.

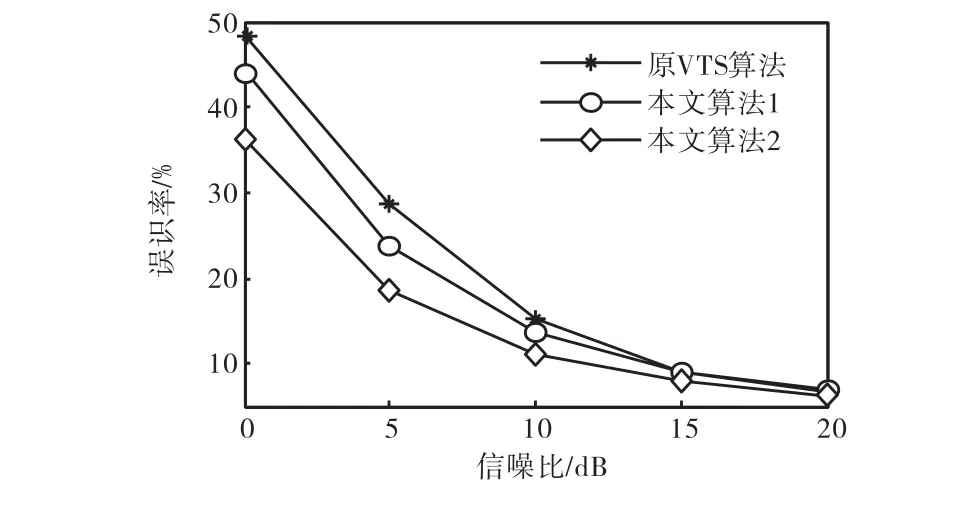
图 1 原 VTS算法和本文算法在 3种测试噪声环境下的平均误识率Fig.1 Averaged word error rates of original VTS algo-Fig. 1 rithm and proposed algorithms for three types Fig. 1 of testing noise

在计算复杂度方面，本文算法相对于对数谱域VTS特征补偿算法[10]，计算量有所增加.因为通过式(9)得到的Um不再是对角矩阵，且本文算法增加了噪声方差估计过程.但本文算法的噪声方差估计是闭式解，其计算量比牛顿法要小得多.相对于目前数字信号处理器件(digital signal processor，DSP)的性能，本文算法增加的计算量是可以接受的.

4 结 语

本文提出了一种基于矢量泰勒级数的倒谱域特征补偿算法.该算法在训练阶段，用一个高斯混合模型描述语音倒谱特征的分布；在识别阶段，首先根据噪声参数调整GMM的均值和方差，使之与测试环境匹配，然后根据含噪特征向量的后验概率，用 MMSE方法估计纯净语音特征参数.含噪语音和纯净语音模型参数之间的非线性关系用一阶矢量泰勒级数近似，噪声参数通过 EM 算法和最大似然准则从含噪语音中估计.该算法可以看成是原对数谱域 VTS特征补偿算法的一种推广.实验结果表明，本文算法对提高语音识别系统的噪声鲁棒性非常有效，能明显提高语音识别系统的识别性能，优于原VTS算法.

［1］Atal B. Effectiveness of linear prediction characteristics of the speech wave for automatic speaker identification and verification[J].Journal of the Acoustical Society of America，1974，55(6)：1304-1312.

［2］Erell A，Weintraub M. Filterbank-energy estimation using mixture and Markov models for recognition of noisy speech[J].IEEE Trans on Speech and Audio Processing，1993，1(1)：68-76.

［3］Acero A.Acoustical and Environmental Robustness in Automatic Speech Recognition[M]. Norwell：Kluwer Academic Publisher，1993.

［4］Sasou A，Asano F，Nakamura S，et al. HMM-based noiserobust feature compensation[J].Speech Communication，2006，48(9)：1100-1111.

［5］Kim W，Hansen J H L. Feature compensation in the cepstral domain employing model combination[J].Speech Communication，2009，51(2)：83-96.

［6］吕 勇，吴镇扬. 基于隐马尔可夫模型与并行模型组合的特征补偿算法[J]. 东南大学学报：自然科学版，2009，39(5)：889-893.

Lü Yong，Wu Zhenyang. Feature compensation algorithm based on hidden Markov model and parallel model combination[J].Journal of Southeast University：Natural Science Edition，2009，39(5)：889-893(in Chinese).

［7］Lü Yong，Wu Zhenyang. Maximum likelihood model adaptation using piecewise linear transformation for robust speech recognition[C]//IEEE International Sympo-sium on Consumer Electronics.Kyoto，Japan，2009：608-610.

［8］Gales M J F. Model-Based Techniques for Noise Robust Speech Recognition[D]. Cambridge: Cambridge University，1995.

［9］Moreno P J，Raj B，Stern R M. A vector Taylor series approach for environment-independent speech recognition[C]//IEEE Int Conf on Acoustics，Speech，and Signal Processing. Atlanta，USA，1996：733-736.

［10］Moreno P J. Speech Recognition in Noisy Environments[D]. Pittsburgh: Carnegie Mellon University, 1996.

［11］Kim D Y，Un C K，Kim N S. Speech recognition in noisy environments using first-order vector Taylor series[J].Speech Communication，1998，24(1)：39-49.

［12］Li J，Deng L，Yu D，et al. High-performance HMM adaptation with joint compensation of additive and convolutive distortions via vector Taylor series [C]//IEEE Workshop on Automatic Speech Recognition and Understanding. Antwerp，Belgium，2007：65-70.

［13］Liao H，Gales M J F. Adaptive training with joint uncertainty decoding for robust recognition of noisy data[C]//IEEE International Conference on Acoustics，Speech，and Signal Processing. Honolulu，USA，2007，4：389-392.

［14］Li J，Deng L，Yu D，et al. A unified framework of HMM adaptation with joint compensation of additive and convolutive distortions[J].Computer Speech and Language，2009，23(3)：389-405.

［15］Dempster A，Laird N，Rubin D. Maximum likelihood from incomplete data via the EM algorithm[J].Journal of the Royal Statistical Society，1977，39(1)：1-38.

Robust Speech Recognition Based on Vector Taylor Series

LÜ Yong，WU Zhen-yang
(School of Information Science and Engineering，Southeast University，Nanjing 210096，China)

The vector Taylor series(VTS)expansion is an effective approach to noise robust speech recognition. However，in the log-spectral domain，there exist the strong correlations among the different channels of Mel filter bank and thus it is difficult to estimate the noise variance from noisy speech proposes. A feature compensation algorithm in the cepstral domain based on vector Taylor series was proposed. In this algorithm，the distribution of speech cepstral features was represented by a Gaussian mixture model(GMM)，and the mean and variance of noise were estimated from noisy speech by the VTS approximation. The experimental results show that the proposed algorithm can significantly improve the performance of speech recognition system，and outperforms the VTS-based feature compensation method in the log-spectral domain.

feature compensation；vector Taylor series；noise estimation；robust speech recognition

TN912.34

A

0493-2137(2011)03-0261-05

2009-11-27；

2010-04-08.

国家自然科学基金资助项目（60971098）.

吕 勇（1979— ），男，博士研究生，lynetwork@gmail.com.

吴镇扬，zhenyang@seu.edu.cn.