鼓泡流化床风帽压力信号的频谱分析

高建强, 姜华伟, 夏 豹, 陈鸿伟

(华北电力大学 电站设备状态监测与控制教育部重点实验室,保定 071003)

当今能源与环境的双重压力使得具有高效率、低污染特点的循环流化床(CFB)锅炉在电厂中占有越来越重要的地位,随之而来的磨损、结渣等问题直接影响机组的安全经济运行,对流化床进行准确的状态监测与分析具有重要意义.然而,由于流化床内气固两相流动过程非常复杂,使得其状态的检测方法远不能满足工程需要.近年来,研究人员普遍认为压力信号是流化床内气固两相流动的一个非常重要的动力学特征,能够反映流化床内颗粒特性、气体性质、反应器几何结构和操作条件等因素的变化[1-4].

目前,CFB炉内压力测点均安装在炉膛壁面上,由于大量物料循环,频繁摩擦撞击测点,使得测点堵塞磨损问题非常严重,造成测量不准确甚至测点损坏[4].流化床风帽入口气流的压力波动与风帽出口上方气固两相流的压力波动密切相关,可以表示为:

式中:p w ci为风帽入口气流的压力;p wco为风帽出口气固两相流的压力;Δpwc为风帽压降.

在风帽结构、流化介质密度以及表观气速一定的条件下,风帽压降为常值[5],风帽入口气流的压力与风帽出口气固两相流的压力为一一对应的关系.流化床运行时风帽出口的床层底部会产生大量气泡并向上运动,造成风帽出口压力的波动,从而使风帽入口压力也相应波动.如果在一次风风室内风帽入口处设置测点,可避免测点与床料直接接触所产生的磨损等问题,从而提高测点工作的可靠性.但目前对风帽入口风压的波动特性与炉内气固两相流动特性间关系的研究还极少[6],其中风帽入口风压的频谱特性分析就是一个重要问题.通过研究风帽入口风压波动能量的分布特性,还可为压力信号采样频率的确定提供依据,从而避免因采样频率设置过大而处理过多的数据,或因采样频率过小致使采集数据中有用信息不全或丢失[7].

笔者在冷态鼓泡流化床试验台上,于风帽入口处设置压力测点,在控制流化风量和床层静高度的情况下,采集不同位置风帽的压力信号,并对采集到的压力信号求自相关函数,然后进行傅里叶变换,将时域信号转换为频域信号,在频域上对信号进行频谱分析.

1 试验系统简介

1.1 试验台

冷态鼓泡流化床试验装置(图1)主要由试验台和数据采集系统组成.试验台本体为三维装置,炉膛由透明的有机玻璃制成,便于观察流动状况,主要部件有炉膛、风室、布风板、钟罩式风帽(布风板上5排8列布置)等.试验台有关尺寸为:流化床截面450 mm×295 mm,炉膛静高度2 000 mm,一次风管直径90mm.

图1 鼓泡流化床试验装置图Fig.1 Experim ental setup of bubbling fluidized bed

1.2 信号采集

试验中压力信号的采集系统由压力变送器、数据采集卡和计算机组成,测点安装在布风板以下风帽入口的壁面上.信号采集过程如下:一次风来自送风机,通过阀门来控制流化风量,并通过安装在一次风管道上的转子流量计来读取流化风量.一次风经过风管进入风室,通过布风板上的风帽进入炉膛,进而流化床内的物料.在位于布风板中心和边缘位置的2个风帽的入口壁面上设置压力测点,控制流化风量和床层静高度,采集不同工况下的压力信号,通过压力变送器将其转换为电信号,然后通过采集卡,将信号转换为数字信号,最后存储至计算机中.

在信号采集过程中,不同研究者所采用压力信号的采样频率各有差异,通过对采集到的压力波动信号进行处理和分析,研究者们普遍得到了鼓泡流化床压力波动信号的实际频率分布在20 H z以内[8].本文实验中所有压力信号的采样频率选择为50 H z.

2 频谱分析方法

采集的信号为随机信号,与确定性信号不同,它既不是有限能量又不是周期的,只能用统计的特征量进行描述.信号的能量无限不代表其功率无限,一个随机信号序列的谱特性可以用功率谱统计来表征.频谱分析是信号分析的核心,随机信号的功率谱可用自相关函数的傅里叶变换来估计[9].

2.1 频谱分析

平稳随机信号的自相关函数的傅里叶变换原理如下:如果x(t)是一个平稳随机信号,它的自相关函数为:

式中:E[.]表示统计平均.

根据维纳-辛钦定理(W iener-Khinchin theorem),平稳随机信号的功率谱密度为自相关函数的傅里叶变换,即

实际上,在估计随机信号的功率谱密度时,由于不知道真实的自相关函数γxx(τ),因而无法按照式(3)计算傅里叶变换得到 Γxx(F).可以计算随机信号的时间平均自相关函数

式中:2T0为观察时间.

如果平稳随机信号的一阶和二阶矩(均值和自相关函数)是各态历经的,那么

这一关系证实了时间平均自相关函数Rxx(τ)可用作对统计自相关函数γxx(τ)的估计.

试验中采集到的压力信号为离散平稳随机信号,设为x(t),则其自相关函数为:

式中:m为延迟.

对自相关函数进行傅里叶变换,即得到信号的功率谱密度.

2.2 信号处理

Matlab信号处理工具箱提供了计算随机信号的相关函数xcorr,其调用格式为:

其中τmax为最大延迟,缺省时,函数的返回值长度为2N-1.在 M atlab中提供了在离散傅里叶变化(DFT)基础上发展起来的快速傅里叶变换(FFT)算法[10],其调用函数 f f t(x,N fft)将时域信号转化为频域信号,从而进行频谱分析.

由于试验采集到的压力信号的直流分量过大,在进行自相关函数傅里叶变换之前,需用detrend函数对信号的直流分量进行处理.图2为Matlab中进行信号处理的流程图.

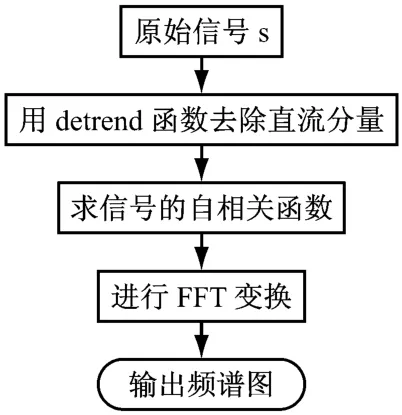
图2 信号处理程序流程图Fig.2 Flow chart of signal processing

3 试验结果与分析

3.1 不同静床高试验

试验条件如下:床料采用粒径为329～438μm的石英砂,流化风量为250 m3/h,即表观气速为0.52m/s.在不同的静床高下,采集位于布风板中心和边壁2个位置风帽入口处的压力信号,并进行频谱分析,结果见图3、图4和图5.

对比图3～图5中不同静床高下不同位置测点信号的频谱图可得出以下结论:

(1)在不同的静床高下,信号的主频均集中在0～10 H z的范围内,属于低频信号,高频部分的值较低,为能量大致均匀分布的噪声信号,可见流化床内的压力波动主要为低频压力波动.

图4 静床高100 mm时测点信号的频谱图Fig.4 Frequency spectrums of collected signals fo r a static bed heigh t of 100 mm

图5 静床高120 mm时测点信号的频谱图Fig.5 Frequency spectrums of collected signals fo r a static bed heigh t of 120 mm

(2)随着静床高的增加,主频的功率谱密度值增大,说明鼓泡流化床压力波动的幅度随静床高的增加会逐渐增大.

(3)当静床高为80 mm和100mm时,布风板中心风帽与边壁风帽入口压力信号功率谱密度的大小和分布的一致性相对较差,中心风帽压力信号功率谱密度明显大于边壁风帽压力信号功率谱密度.随着静床高的增加,中心风帽与边壁风帽入口压力信号功率谱密度的大小和分布的一致性越来越好.原因是当流化床静床高过低时,床层底部离床层表面较近,大量床料颗粒因气泡在床面爆破被夹带着抛掷向上,其中相当大一部分颗粒在经过一定高度后由壁面附近陆续落回床面,而后沿壁面下滑,影响了床层底部边壁附近气泡的长大,从而使床层底部边壁附近压力波动相对中心区域小.随着静床高的增加,这种影响越来越小,使床层流化趋于均匀,流化稳定性变好.

3.2 不同表观气速试验

试验条件如下:床料采用粒径为329～438μm的石英砂,为避免静床高过低对床层流化均匀性的影响,选择静床高为120mm,通过阀门控制流化风量.在不同的表观气速下,采集位于布风板中心和边壁2个位置风帽入口处的压力信号,并进行频谱分析,结果见图6～图8.

图6 表观气速0.21 m/s时测点信号的频谱图Fig.6 Frequency spectrum s of collected signals for a superficial gas velocity of 0.21m/s

图7 表观气速0.42m/s时测点信号的频谱图Fig.7 Frequency spectrums of collected signals fo r a superficial gas velocity of 0.42 m/s

图8 表观气速0.63m/s时测点信号的频谱图Fig.8 Frequency spectrums of collected signals fo r a superficial gas velocity of 0.63 m/s

对比图6～图8中不同表观气速下不同位置测点信号的频谱图可得出以下结论:

(1)在不同的表观气速下,信号的主频均集中在0～10Hz的范围,再次验证了流化床内压力波动主要为低频压力波动.

(2)随着表观气速的增加,信号的主频对应的功率谱密度值增大,说明表观气速的增加导致鼓泡流化床内压力波动更加剧烈,这是由于在鼓泡流态化下,表观气速的增大使床内产生的气泡直径增大,大气泡的产生和运动加大了床内压力波动的幅度.

(3)当表观气速为0.21m/s时,布风板中心风帽与边壁风帽入口压力信号功率谱密度的大小和分布的一致性相对较差,中心风帽压力信号功率谱密度明显大于边壁风帽压力信号功率谱密度.随着表观气速的增大,中心风帽与边壁风帽入口压力信号功率谱密度的大小和分布的一致性越来越好.原因是边壁风帽靠近炉膛的边壁,其出口的流化速度受边界层的影响比炉膛中心区域流化速度小,因此产生气泡的直径也比炉膛中心区域的小,压力波动的幅度也相对较小.边界层厚度与来流速度存在如下关系

式中:δ为边界层厚度;L为炉膛壁面特征长度;Re为雷诺数;u为来流速度;ν为运动黏度.

温度不变时,ν的变化可忽略不计,边界层厚度δ随来流速度u的增大而减小,因此随着床层表观气速的增大,边壁风帽出口的流化速度逐渐接近中心风帽出口的流化速度,从而使床层流化更加均匀.

4 结 论

(1)风帽入口压力信号的变化与流化床内静床高和表观气速等参数的变化密切相关;风帽入口压力波动能量主要表现为低频压力波动.

(2)只要压力信号的采样频率不低于50 Hz,即可保证所采集信号的有用信息的完整性,可为工程应用提供参考.

(3)通过采集、分析鼓泡流化床风帽入口压力波动特性,可以在线预测流化床内的工作状况.

[1] 赵贵兵,陈纪忠,阳永荣.流化床压力脉动信号时间延迟相关性[J].化工学报,2002,53(12):1281-1287.ZHAO Guibing,CHEN Jizhong,YANG Yongrong.Delay time correlation of time of pressure fluctuations in bubb ling fluidized bed[J].Journal of Chem ical In-dustry and Engineering,2002,53(12):1281-1287.

[2] 兰静,沈来宏.基于小波变换的鼓泡流化床压力波动信号的分析[J].锅炉技术,2003,34(4):42-46.LAN Jing,SH EN Laihong.W avelet ana lysis of p ressure fluctuation in a bubbling fluidized bed[J].Boiler Technology,2003,34(4):42-46.

[3] 张少峰,王琦,高川博,等.液固两相外循环流化床压力波动信号的统计及频谱分析[J].过程工程学报,2006,6(6):878-883.ZHANG Shaofeng,W ANG Qi,GAO Chuanbo,et a l.Statical and f requency analysis of p ressure fluctuation in linquid-solid ex terior circu lating fluidized bed[J].The Chinese Journal of Process Engineering,2006,6(6):878-883.

[4] CHEN Y,TIAN Z,M IAO Z.Detection o f singularities in the p ressure fluctuations of circu lating fluidized beds based on w aveletmodulusmaximum method[J].Chem ical Engineering Science,2004,59(17):3569-3575.

[5] 岑可法,倪明江,骆仲泱,等.循环流化床锅炉理论设计与运行[M].北京:中国电力出版社,1997:66-78.

[6] 高建强,姜华伟,陈鸿伟,等.鼓泡流化床风帽压力波动信号的小波包分析[J].动力工程学报,2010,30(10):763-767.GAO Jianqiang,JIANG H uaw ei,CHEN Hongwei,etal.Wavelet packet analysis on pressure fluctuation signal of nozzle button in bubbling fluidized bed[J].Journal of Chinese Society of Power Engineering,2010,30(10):763-767.

[7] 朱浩,陈喜阳,李友平,等.水电机组在线监测中同步整周期采样实现策略[J].电力系统自动化,2007,31(4):80-84.ZHU H ao,CHEN Xiyang,LI Youping,etal.Application of synchronous w hole-periodic samp ling in the hyd ropow er on-linemonitoring system[J].Automation of Electric Power Systems,2007,31(4):80-84.

[8] 赵贵兵,陈纪忠.流化床压力波动混沌性质探讨[J].化工学报,2002,53(6):655-659.ZHAO Guibing,CHEN Jizhong.Chaotic nature of pressure fluctuation in f luidized bed[J].Journal of Chem ical Industry and Engineering,2002,53(6):655-659.

[9] 李庚银,陈志业,宁宇.快速傅里叶变换的两种改进算法[J].电力系统自动化,1997,21(12):37-40.LIGengyin,CHEN Zhiye,NING Yu.Two modified algorithms for fast Fourier transform[J].Automation of Electric Power Systems,1997,21(12):37-40.

[10] 董静薇,于广艳.基于Matlab的FFT频谱分析及IIR数字滤波器设计[J].软件导刊,2008,7(10):128-129.DONG Jingwei,YU Guangyan.FFT spectrum analysis and IIR digital filter design based on M atlab p rogramm ing[J].Software Guide,2008,7(10):128-129.