矩阵分解方法的探究

王群英

(肇庆科技职业技术学院基础课教学研究部，广东肇庆 526110)

1 矩阵分解的概述

矩阵是数学中最重要的基本概念之一，是代数学的一个主要研究对象，也是数学研究及应用的一个重要工具。矩阵是线性代数中最为重要的核心内容，很多问题都可以归结为矩阵并最终通过矩阵解决。在近代数学、工程技术、信息处理、经济理论管理科学中，也大量涉及到矩阵理论的知识，矩阵分解是实现大规模数据处理和分析的一种有效工具，在工程计算中具有重要的实际意义。矩阵理论自然就是学习和研究上述学科必不可少的基础之一。另一方面，矩阵理论发展到今天已经形成了一整套的理论和方法，内容非常丰富。矩阵分解是指根据一定的原理用某种算法将一个矩阵分解成若干个矩阵的乘积或者一些矩阵之和，矩阵分解对矩阵理论及近代计算数学的发展起了关键的作用。寻求矩阵各种意义下的分解形式，是对与矩阵有关的数值计算和理论都有着极为重要的意义。因为这些分解式的特殊形式，一是能明显地反映出原矩阵的某些特征;二是分解的方法与过程提供了某些有效的数值计算方法和理论分析依据。这些分解在数值代数和最优化问题的解决中都有着十分重要的角色以及在其它领域方面也起着必不可少的作用。

2 矩阵的分解方法

2.1 矩阵LU分解

LU分解，设A=(aij)是n阶可逆矩阵，如果A的对角线下(上)方的元素全为零，即对i＞j，aij =0(对i＜j，aij=0)，则称矩阵A为上(下)三角矩阵，上三角矩阵和下三角矩阵统称为三角矩阵。如果有下三角矩阵L和上三角矩阵U，使得A= LU，则称A能做三角分解，并且称A=LU为A的三角分解或者LU分解[1]。LU分解的定理:设A是n阶非奇异矩阵，则存在唯一的单位下三角矩阵L和上三角矩阵U，使得A=LU的充分必要条件是A的所有顺序主子式均非零，即

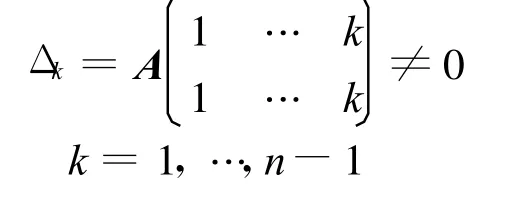
LU分解可以用直接法导出A=LU的分解公式，将A=LU写成

比较等式两端的第i行和第j列元素，可得

上式利用了lii=1，从而

当j=i+1，i+2，…，n时

从而

LU分解的初等变换消元法:设可逆矩阵A的n个顺序主子式非零，则存在可逆矩阵P，使PA=U，A=P-1U=LU，其中P是一系列初等行矩阵之积(对应于初等行变换)，L=P-1是下三角矩阵，U为上三角矩阵，求P，U可用如下做法:

例1:求矩阵

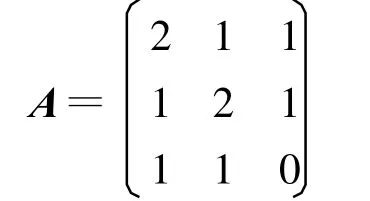
的LU分解。

解:对矩阵(A|I)做初等行变换

可得

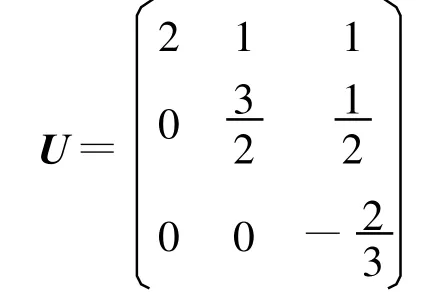
即得A=LU。

2.2 矩阵的QR分解

矩阵的QR分解(正交三角分解)在解决最小二乘问题、特征值计算、广义逆矩阵的计算方面，都是十分重要的[2]。以下为矩阵的QR分解:设A是n阶可逆实矩阵，则A可惟一分解为

其中，Q为正交矩阵(QTQ=QQT=1，或Q-1= QT)，R是主对角元素都是正数的上三角矩阵，称该分解为对A的正交三角分解。A是m×n矩阵，且A为列满秩，即r(A)=n，则有

其中，Q m×n的n个列向量是标准正交的，R为正对角元的n阶上三角矩阵。

我们看QR分解是不是唯一的。记A= [a1，a2，…，an]，ai是矩阵A的第i个列向量，因为矩阵A非奇异，所以向量组a1，a2，…，an线性无关，应用Gram-Schmidt正交化方法将线性无关向量组a1，a2，…，an化为标准正交向量组q1，q2，…，qn，则可得

则Q为正交(酉)矩阵，R为非奇异实(复)上三角矩阵，由Gram-Schmidt正交分解式，有A=QR，这就证明了QR分解的存在性。

设矩阵A有两个QR分解

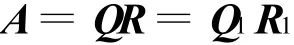
其中，Q，Q1为正交(酉)矩阵，R，R1为非奇异上三角矩阵，则

其中，D=R1R-1为非奇异上三角矩阵，于是

这说明D为酉矩阵，比较等式

的对角元，可导出D为对角矩阵，并且对角元的模全等于1，于是

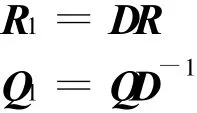
如果在非奇异矩阵A的QR分解中规定上三角矩阵R的各个对角元的符号(例如全为正数)，则A的QR分解是惟一的。

矩阵的QR分解有多种。常见的有Schm idt (施密特)正交分解法、Givens(吉文斯)正交分解法和Household(豪斯霍德)正交分解法。

施密特正交分解法:设可逆矩阵(或列满秩)A的列向量为α1，α2，…，αn，施以Schmidt标准正交化使β1，β2，…，βn为正交组。

得

因为ε1，ε2，…，εn为标准正交组，Q=(ε1，ε2，…，εn)为正交阵。

例2:用Schmidt正交化方法求矩阵

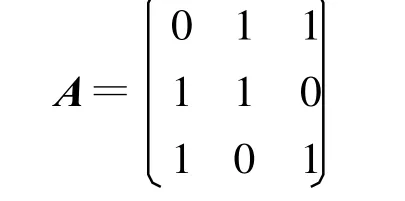
的QR分解。

解:令

由Schm idt正交化公式，得

因而可得

求解公式

得到

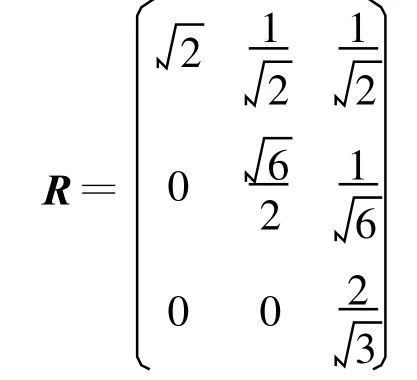
即得

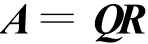
吉文斯方法:利用初等旋转矩阵的性质，即用Rij左乘矩阵A时，仅影响A的第i行和第j行，且选适当的Rij，就可以消去A的一个非零元素。一般地说，作一次旋转可以消去一个非零元素。如果在作下一次旋转时不会影响前面已化为零的元素，即不会重新又变为非零，那么，借助于初等旋转阵将A约化成上三角阵就有希望。事实上，只要注意运算顺序，完全能办到。

2.3 矩阵的谱分解[3]

2.3.1 单纯矩阵的谱分解

n阶单纯矩阵A有n个线性无关的特征向量，不妨设λ1，λ2，…，λn是A的n个特征值;x1，x2，…，xn是A的n个线性无关的特征向量，且有

令

则A=PVP-1两边取转置得AT=(PT)-1VPT，这表明AT也与对角矩阵相似。因此，设y1，y2，…，yn是AT的n个线性无关的特征向量，即

把上式两端取转置得

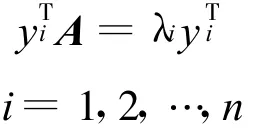
根据上式，我们称yTi是A的左特征向量，称xi是A的右特征向量。由式AT=(PT)-1VPT知

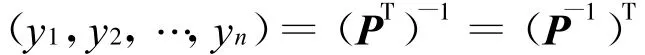
两端转置得

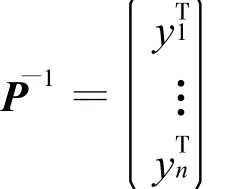
代入

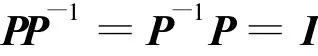
得

此即

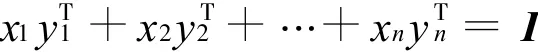
比较两端即有

与式

代入A=PVP-1得

令

则得

上式称为单纯矩阵A的谱分解。即A分解成n个矩阵Gi之和的形式，其线性组合系数是A的谱(所有的特征值)。

2.3.2 谱分解的相关定理[4]

定理1 设A是n阶单纯矩阵，λ1，λ2，…，λr是A的r个相异的特征值，则A可以进行满足下列性质的谱分解[7]。

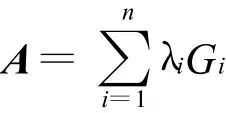
有

其中

根据式

得

再由

得

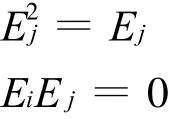
即所有的式子得证。

例3:求矩阵

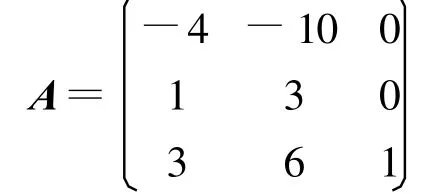
的谱分解。

故A的特征值为

对于λ1=-2，由

得

特征向量

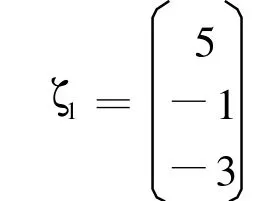
对于λ1=-2，由

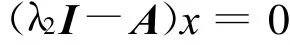
得

特征向量

所以

取

则

2.4 矩阵的奇异值分解

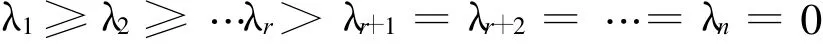
1)m×n矩阵A的奇异值的个数等于列数n (因AHA的阶数为n);

2)A的非零奇异值的个数等于 rank A(因rank AHA=rank A)。

以下给出矩阵A的奇异值分解定理。

定理2 设A∈Cm×nr ，则存在m阶酉矩阵U和n阶酉矩阵V，使得

其中E=diag(σ1，σ2，…，σr)，而σi(i=1，2，…，r)为A的正奇异值，称

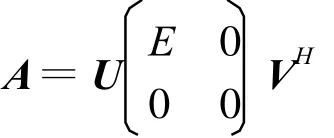
为A的奇异值分解[6]。

由正规矩阵的充要条件存在n阶酉矩阵使得

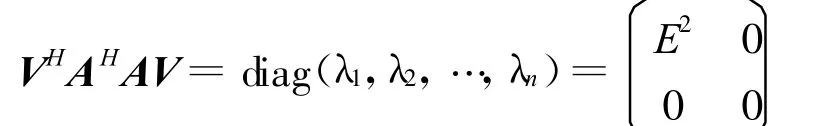
记V=(V1，V2)。其中V1∈Cn×r，V2∈Cn×(n-r)代入上式

于是

上面第2式说明AV2=0，令U1=AV1 E-1。则由第1式得U1=I说明U1为次酉矩阵，它的r个列向量是两两正交的单位向量，取U2∈Cm×(n-r)，使U =(U1，U2)为m阶酉矩阵，即

再注意到AV=U1 E，AV2=0，最后有

例4:求矩阵

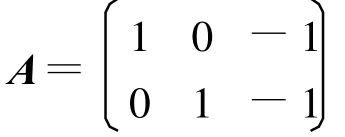
的奇异值分解。

解:因为

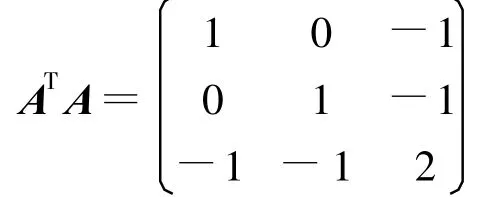
所以ATA得特征值为3，1，0，于是A的奇异值为σ1=，σ2=1且ATA的正交单位特征向量分别为

令

则

从而可得A的奇异值分解为

[1] 史荣昌，魏丰.矩阵理论[M].北京:北京理工大学出版社，2008:183-211.

[2] 方保镕，周继东，李医民.矩阵论[M].北京:清华大学出版社，2004:291-324.

[3] 戴华.矩阵论[M].北京:科学出版社，2001:117-139.

[4] 李新，何传江.矩阵理论及其应用[M].重庆:重庆大学出版社，2005:130-145.

[5] 罗小桂.矩阵奇异值分解及其应用[J].井冈山学院学报，2005，12(4):133-135.

[6] D D Lee，H S Seung.Learning the parts the objects with nonnegative matrix factorization[J].Nature，1999，401:213-263.

[7] 李建东.矩阵QR分解的三种方法[J].吕凉学院学报，2009，25(1):16-19.

[8] 徐泰燕，郝玉龙.非负矩阵分解及其应用现状分析[J].武汉工业学院学报，2010(1):110-115.