二阶常微分方程边值问题的格林函数求法

刘丽环， 常 晶， 高艳超

(空军航空大学基础部，吉林长春 130022)

0 引 言

利用拓扑度理论、半序方法以及临界点理论可以研究常微分方程多个解的存在性，利用不动点定理和单调迭代法可以研究脉冲常微分方程解的存在性。这些年来，这方面的结果有很多[1-5]。格林函数方法是求解常微分方程的一种重要方法，它的实质是把常微分方程加上边值条件转化为一个积分方程，通过研究格林函数的性质和函数非线性项的性质求所述的非线性常微分方程边值问题的解[6-8]。文中主要应用格林函数方法以及压缩映射原理证明下面二阶常微分方程

解的存在惟一性。

1 主要结果及证明

定理1 若方程(1)中f(t，y(t)，y′(t))连续，且满足Lipschitz条件，即

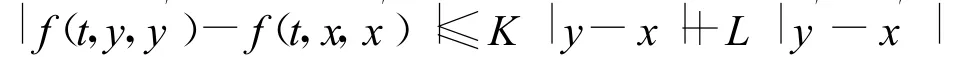
且若

则方程(1)存在惟一解。

证明 首先构造(1)的G reen函数为

则方程(1)等价于

与

因此

并且

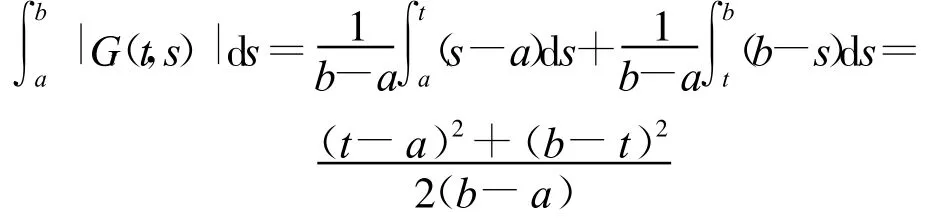
此函数在t=a与t=b处达到最大值，由此可得

接下来需要寻找一个函数空间，使得y(t)以及y′(t)在此空间下均收敛。取S为[a，b]上的C1函数空间，取u∈S，并定义其范数为:

其中K与L为

中的Lipschitz常数。下面需要构造映射 T:S→S，既需要证明:(1)只要u(t)是C′的，则Tu(t)就是C′的;(2)T为压缩映射。为此构造差商:

则

且关于t连续，故Tu(t)就是C′的。我们还需要证明(2)成立。

构造

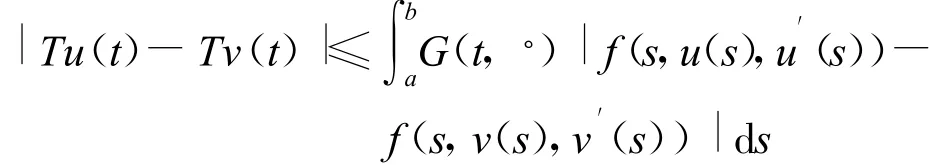
因

故可以推得

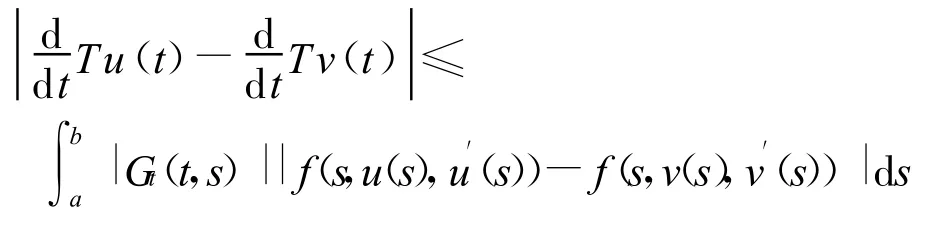
由Lipschitz条件

可得。

又因

从而

故当

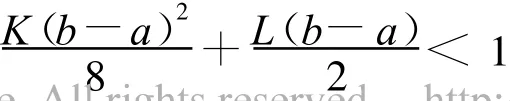
时，‖Tu-Tv‖≤α‖u-v‖，α＜1，故T为压缩映射，从而方程(1)有惟一解，定理得证。

注1:若方程(1)的边值条件改为

则其相应的G reen函数为:

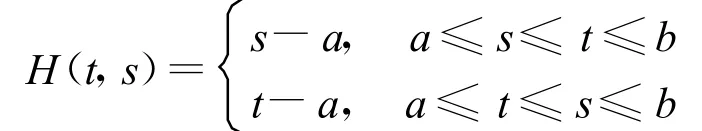
则问题等价于

和

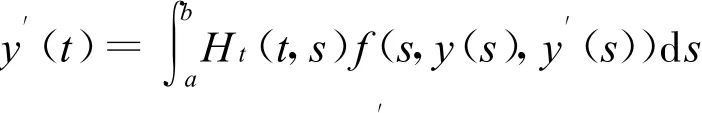
注2:若f中不含有y′时，即

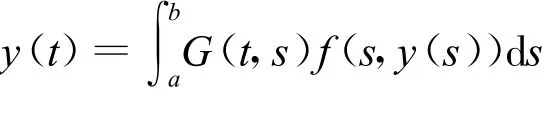
其函数空间S的范数此时可定义为

这是S为完备的赋范线性空间，显然u(t)是连续的，则Tu(t)就是连续的，这意味着T将S映射到自身，接下来确定何时T是S上的一个压缩映射。首先

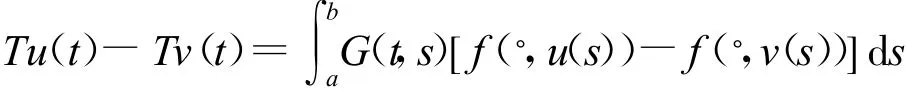
如果使用G(t，s)≥0，及Lipschitz条件

有

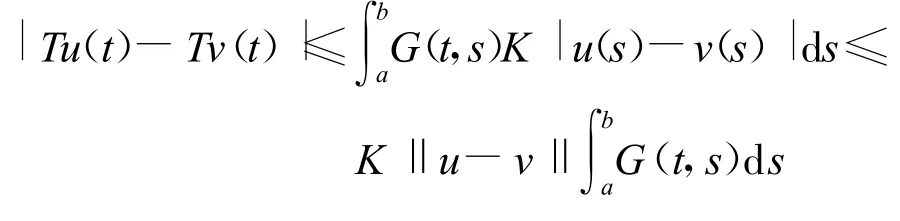
由于

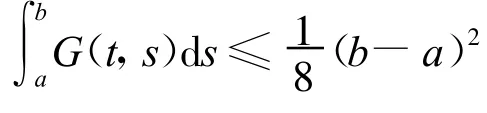
因而

其中

引例:考虑

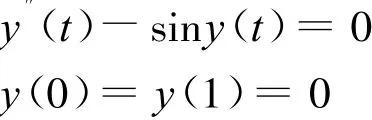
这时

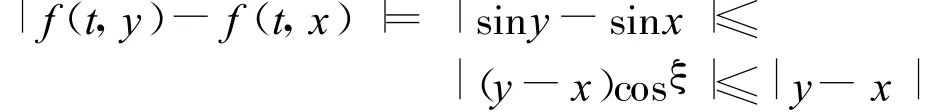
[1] 程纲.二阶微分方程边值问题的多重正解[J].应用数学学报，2003，26(2):272-279.

[2] Dong H SF.Oppenheimer existenceand uniqueness results for some nonlinear boundary value prob lems [J].J.Math.Anal.App l.，1996，198:35-48.

[3] Erbe L H，Kong Q.Boundary value p rob lem s for singular second order functional differential equations[J].J.Comp.App l.M ath.，1994，53:377-388.

[4] LiY.On the existence and nonexistence of positive solutions for nonlinear Strum-Liouville boundary value prob lems[J].J.Math.Ana l.Appl.，2005，304:74-86.

[5] Li Y.Positive so lutions of second order boundary value problem s with sign-changing nonlinear terms [J].J.M ath.Anal.App l.，2003，282:232-240.

[6] Liu Yan Sheng，Yu H ui M in.Existence and uniqueness of positive solution for singular boundary value p roblem[J].Computers and M athematics with A pp lications，2005，50:133-143.

[7] BaiZhan Bing，GeW eiGao.Existence of three positive solutions for some second order boundary value problems[J].Computers and Mathematics with App lications，2004，48:699-707.

[8] Li Fu Y i，Zhang Q i，Liang Zhao Ping.Existence and multip licity of solutions of a kind of fourth order boundary value p rob lem[J].Nonlinear Analysis，2005，62:803-816.