Heston模型的对数效用无差别定价

张东云

(河南师范大学经济与管理学院，河南新乡 453007)

0 引 言

效用无差别定价是一种新的定价方式，它以效用最大化为最优性准则，利用考虑未定权益和不考虑未定权益两种不同投资机会的相关性得到的一种定价方法，首次由Hodegs和Neuberger[1]1989年提出。当效用函数为指数效用函数时，无差别定价与最小熵等价鞅测度有相关性，因此，对于指数效用函数的无差别定价得到了很多研究成果。对于指数效用的无差别定价，效用无差别定价主要通过两种方法进行研究:一种是以随机控制理论为基础，利用动态规划方法对效用无差别定价进行研究[2-4];另一种是鞅方法，利用熵准则和最优投资组合问题[5]的对偶性来研究效用无差别定价[6]。由于对数效用函数中对期末财富的非负性的要求，使得对数效用函数的无差别定价的研究几乎是一片空白。文中利用动态规划方法对Heston模型的对数效用函数的无差别定价进行了初步探索。

1 市场模型

Heston模型是一种比较特殊的随机波动率模型，文献[7]讨论了该模型的最优投资组合问题，下面利用文献[7]给出Heston模型。

给定概率空间(Ω，F，F t，P)，市场中的所有信息集用滤子Ft表示，Ft满足通常条件。投资者在投资区间[0，T](T∈R+)内可以连续交易。市场上有两种资产:一种是无风险资产，其t时刻的价格S0(t)≡1;另一种是风险资产，假设风险资产价格过程S(t)满足Heston模型，即风险资产的价格满足随机微分方程:

其中λ，α和β为正的常数，-1＜ρ＜1，μ(y)/σ(y)=ζy，W(t)与(t)是相互独立的Brownian运动。

给定交易策略π(t)，策略集记为A(t)，则相应于交易策略π(t)的财富过程X(t)满足随机微分方程

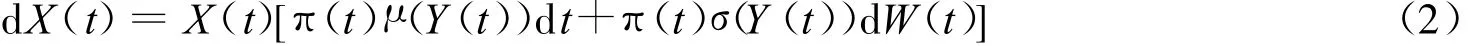
考虑对数效用函数

给定未定权益C T，考虑如下最优投资组合问题

和

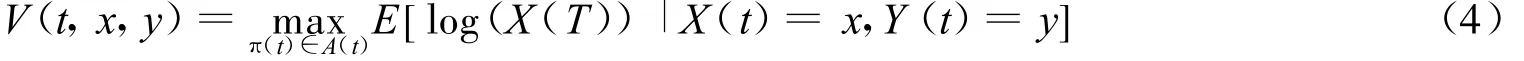
定义1 对于未定权益CT，满足

Λ(t)称为未定权益C T在t时刻的对数效用无差别定价。

2 Heston模型的对数效用无差别定价[8]

定理1 假设风险资产价格过程满足Heston模型，则欧式未定权益C T的对数效用无差别定价满足:

边界条件为

证明:首先给出V(t，x，y)的HJB方程

边界条件为

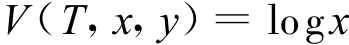
由一阶条件得最优策略

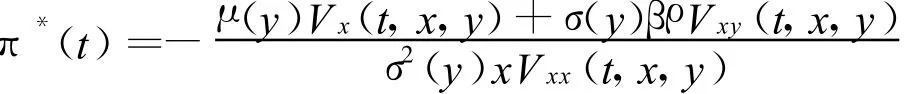
将上式代入式(7)得

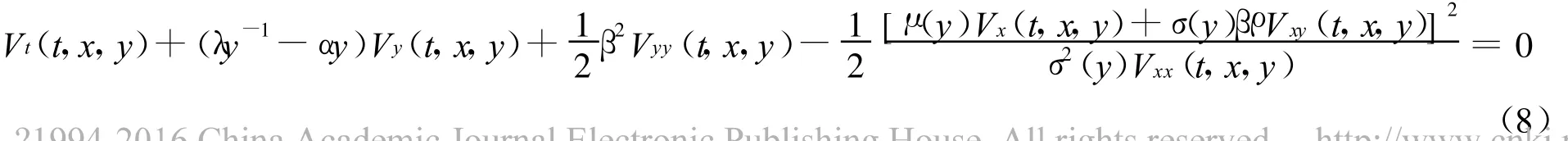
假设V(t，x，y)是可分离的，即

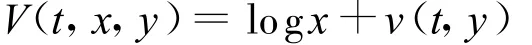
将其代入式(8)得

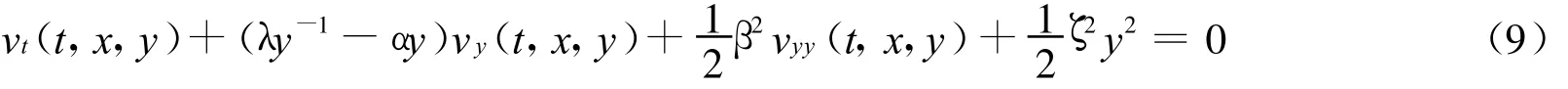
边界条件为

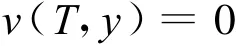
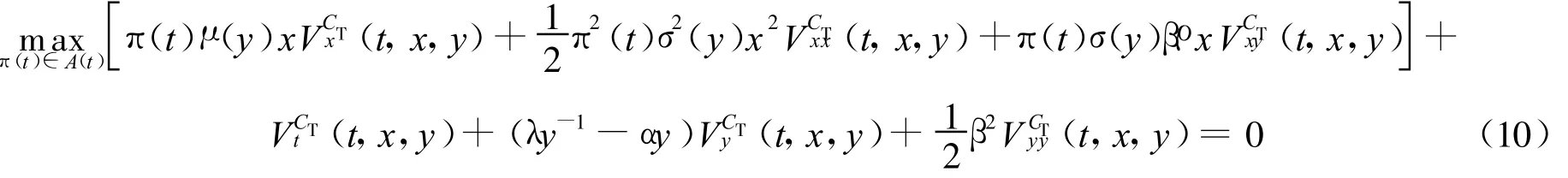
边界条件为

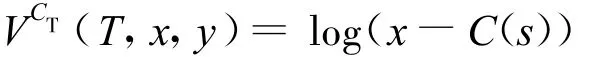
由一阶条件得最优策略

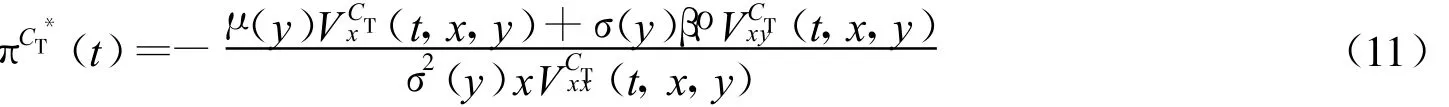
将上式代入式(10)得

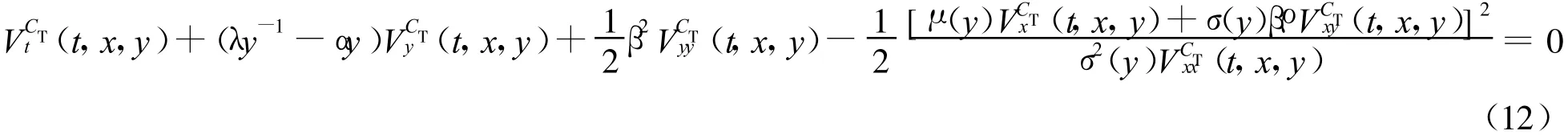
由定义1可得

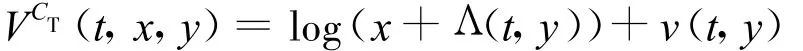
将上式代入式(12)，由式(9)得

边界条件为

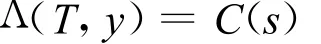
由式(6)可知，Heston模型的对数效用无差别定价也与投资者的初始财富x有关。

[1] Hodges S D，Neuberger A.Op timal rep lication o f contingent claims under transaction costs[J].Review of Futures Markets，1989(8):222-239.

[2] M usiela M，Zariphopoulou T A.An exam ple of indifference prices under exponential preferences[J]. Finance and Stochastic，2004，7(8):229-239.

[3] 闫海峰，刘利敏，杨建奇.随机波动率模型的效用无差别定价和套期保值策略[J].系统工程学报，2007， 22(4):379-384.

[4] Marek M，Thaleia Z.A valuation algorithm for indifference p rices in incompletemarkets[J].Finance and Stochastics，2004，8(3):399-414.

[5] 邢蕾，赵鹏飞.Q对称熵损失函数下几何分布参数估计[J].长春工业大学学报:自然科学版，2008，29 (6):614-616.

[6] Delbaen F，G randits P，Rhein lander T，et al.Exponentialhedging and entropic penalties[J].Mathematical Finance，2002(12):99-123.

[7] 李玉萍，刘利敏.Heston模型的最优投资组合[J].扬州大学学报:自然科学版，2007，10(3):25-27.

[8] 叶中行，林建忠.数理金融:资产定价与金融决策理论[M].北京:科学出版社，2007.