采用选择性分段PCA算法的高光谱图像异常检测

赵春晖，胡春梅，石 红

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

高光谱图像具有“图谱合一”特性，成像波段密集且连续，具有很高的光谱分辨率，在检测、识别地面的低空间分辨率目标方面具有独特的优势.异常检测算法不需要利用光谱的先验知识，而能直接检测出与周围景物光谱存在明显差异的光谱信号所在位置作为异常点，由于目标先验光谱信息很多实际情况下难以获得，所以异常检测算法对于未知场景中光谱特性未知目标的检测识别具有重要意义［1］.常用的异常检测算法主要有RX检测算法，正交子空间算法(OSP)，约束能量最小化算法(CEM)，低概率检测算法(LPD)等.利用高光谱图像对目标进行检测的常用算法通常在检测之前先对图像进行预期的处理，如将其投影到特征向量空间中，选取其信息量较大的波段用于后续的异常检测，但是在预期处理的过程中往往会遇到这样的问题:高光谱图像各波段在成像过程中受波段响应特性、大气吸收和成像系统噪声等因素的影响不同，各波段反映的光谱特性不同，且相邻波段具有很强的相关性，而在变换的过程中经常包含对各个波段中背景与目标之间光谱差异的加权或乘方加权等运算，由于地物光谱的复杂性，由不同的光谱特性所得到的最终运算结果可能相近［2］，且需要消除波段之间很强的相关性，并选取其中包含目标信息较多的波段用于异常检测.因此，本文算法先将一组多维的高光谱数据根据波段间的相关性划分成多组波段子集数据，并分别对每一波段子集进行特征提取，去除波段之间的相关性，这样使得高光谱数据的可分性投影到了各波段子集上，然后在各波段子集中分别寻找出局部平均奇异度(LAS)最大的波段，并将其映射到高维的特征空间中，充分利用数据的高阶统计量对目标进行检测，最终实现异常检测.

1 算法原理

1.1 选择性分段PCA算法

本文算法主要思想是通过在各波段子集中选取局部平均奇异度最大的主成分用于后续的KRX异常检测，使得在减少数据量的同时，最大限度地保留异常目标的信息，从而在降低计算复杂度的同时尽可能地提高检测性能.算法实现流程如图1所示.

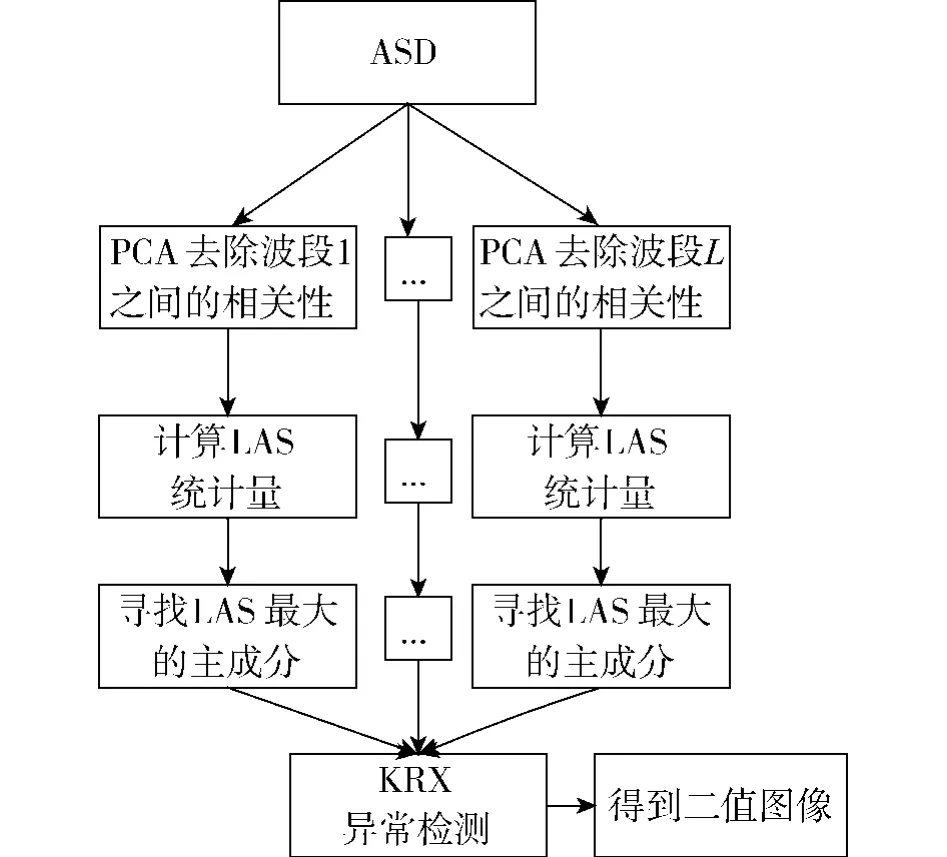
图1 算法流程图Fig.1 Algorithm flowchart

高光谱图像各波段之间的相关性大小不一样，且各波段反映的光谱特性不同［2］.根据这一特性，为克服不同光谱特性所造成的运算结果相近的问题，则应根据波段之间的相关性(如图2所示)，采用自适应子空间分解(ASD)算法在相关性极小值点小于阈值处，将一组多维的高光谱数据按波段之间的相关性大小分为若干个独立的波段子集，然后分别在各个相关性较大的波段子集内进行主成分分析［3］去相关处理.

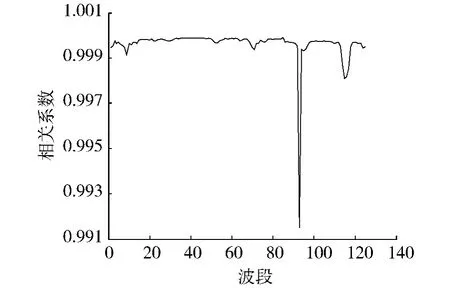
图2 高光谱图像相邻波段之间的相关系数Fig.2 Correlation coefficient of adjacent bands for hyperspectral image

主成分分析是均方差最小意义上的最佳正交变化，亦可以看作是以均方差最小为投影指标的投影寻踪，在几何意义上相当于进行空间坐标的旋转，第一主成分是波谱中数据散布最集中的方向，第二主成分是与第一主成分正交且数据散布次集中的方向，以此类推.它能使变换后产生的新分量正交或者不相关，均方差最小且能量最集中［3］.每一个高光谱图像都可被看作是一个采样向量，采样样本的数目为原始波段的数目L，即将高光谱图像数据整理成L×N矩阵X，X=［x1x2…xN］，其中xi代表一个像素点，每一行代表一个波段.估算矩阵X的协方差矩阵C，并将估算的背景协方差矩阵进行特征值分解为

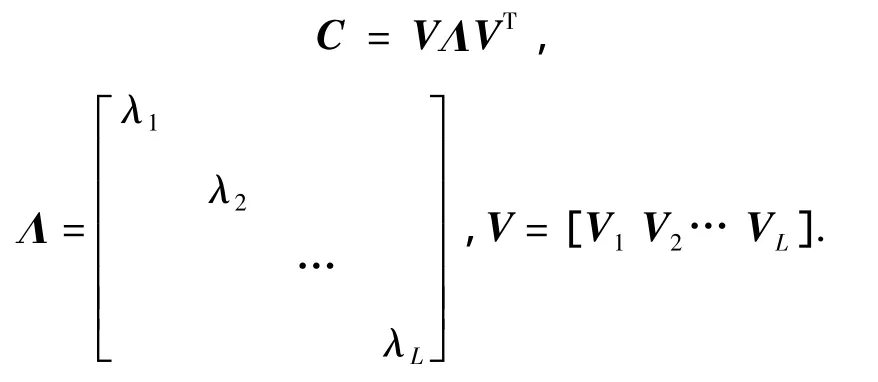
式中:Λ的对角元素为背景协方差矩阵C的非零特征值λi;V为非零特征值所对应的特征向量，由于其特征值是一个对角阵，则其各特征向量之间是相互正交的，或者是不相关的.将采样数据X投影到特征向量V上，从而得到Y=VT·X，使得新分量之间是正交的或者是不相关的.

利用三阶累积量(偏度)和四阶累积量(峭度)来衡量每个主成分的非高斯特性.在异常检测中，若某局部窗口服从高斯分布，则相应的偏度和峭度都为零［4］.如果某局部窗口中包含有异常目标，则高斯分布就会被打破，偏度和峭度的绝对值就会变得很大.根据这一特性，用局部平均奇异度(LAS)［5］来度量各主成分的非高斯特性，即包含异常目标的可能性大小，并用NLAS来标记.实验中根据图像的大小适当地选择窗口的大小，最终采用一个10×10的窗口模板来遍历每一个主成分.当在某局部窗口内其偏度和峭度均大于设定的阈值时，该主成分的局部平均奇异度NLAS自加1，用这个窗口模板遍历该主成分，统计该主成分的局部平均奇异度NLAS.所得的NLAS越大，则该主成分的非高斯特性越强，所包含的异常目标信息越多，即选取这样的主成分用于后续的异常检测［6］.

1.2 KRX算法

RX算法是应用最为广泛的一种异常检测算法，而将原采样数据通过非线性映射函数映射到高维(可能是无限维)的特征空间中，就形成了核空间中的KRX算法［7-8］，其算子可表示为

式中:Cbφ和μbφ分别为特征空间中背景协方差矩阵和均值的估计.经过特征值分解后得到核空间RX算法的表达式为

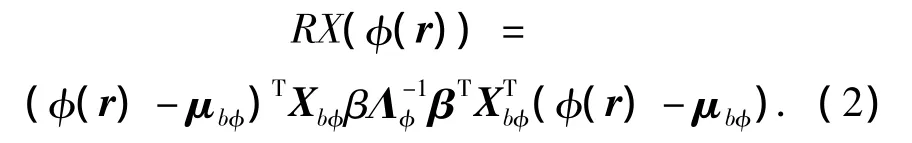
式中:β=［β1β2… βN］T为经过核矩阵K相应特征值的平方根归一化之后的特征向量.但是由于数据的维数很高(甚至是无限维的)，不能直接通过非线性映射函数φ将原始数据映射到高维特征空间中来实现该算法.为了避免直接计算式(1)，采用核技术［9-10］，用原始数据空间中的核函数来间接地实现高维特征空间中的内积，即由

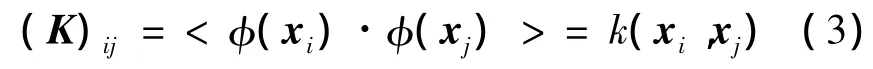
来间接地计算式(2).由文献［5-6］和KPCA［8］得到KRX算法最后的检测算子为

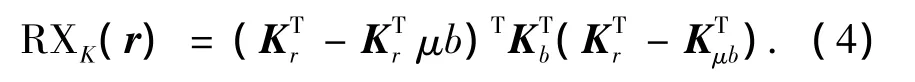
式中:

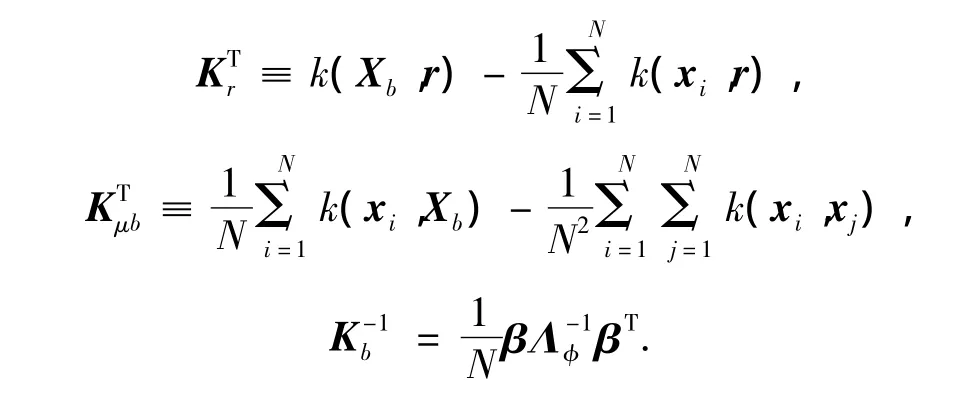
2 仿真结果及其分析

2.1 数据描述

为验证本文提出的异常检测算法的有效性，笔者利用AVIRIS高光谱数据源进行了仿真实验.该图像覆盖了从可见光到短波红外的光谱范围，除去水的吸收带和信噪比较低的波段后，余下的126个波段参与仿真实验.所用实验图像大小为100× 100，该图中包含了38个异常小目标.所用实验图像的第10个波段以及地面目标分布如图3、4所示.

图3 第10波段Fig.3 The tenth band

图4 地面目标分布图Fig.4 Ground target distribution

2.2 实验结果与分析

在实验中，首先对数据进行归一化处理，之后计算相邻波段之间的相关性，根据相关性的大小从相关性值的极小值点小于设定的阈值处将高光谱图像分为5个波段子集，波段子集1为第1－8波段，波段子集2为第9－70波段，波段子集3为第71－94波段，波段子集4为第95－114波段，波段子集5为96－126波段.在每一个波段子集上进行主成分分析，消除波段之间的相关性，选取局部平均奇异度最大的波段，综合起来作为最终用于KRX异常检测的数据源.

图5 SSPCAFig.5 SSPCA

在进行KRX算法检测时，采用局部同心双窗口，其中外窗为背景检测窗，用来计算背景特性，内窗为目标检测窗，中心点为待检测像素点，并根据图像的大小和空间分辨率，将背景检测窗口大小定为11×11像素，目标检测窗口大小定为3×3像素.对于核函数的选择，本文采用径向基核函数，在核函数选择之后其参数的确定是及其重要的，这是因为参数合适选取可使得数据体现所需要的非线性特性.本实验中需要确定的参数为径向基核函数的宽度σ，由于最优参数的选择还没有完善的指导理论，因此文中的参数是通过大量的实验仿真比较其结果最终确定的，本文将径向基核函数的宽度σ定为0.07.

在利用式(4)得到各像素点对应的检测值之后，由于目标都是孤立和较小的，因此采用形态学方法提取出像素点较少的目标区域.利用本文提出的算法(SSPCA)检测最终得到的二值图像如图5所示.为了便于分析比较，试验中还对原始数据直接进行KRX算法和综合各波段子集中能量最大的波段(记为SMIPCA)用于KRX检测进行了仿真，并进行形态学处理.在相同阈值下其检测效果分别如图6、图7所示.

图6 KRXFig.6 KRX

从图5、6的比较可以看出，本文提出算法的检测性能明显优于其他2种.这是因为直接将KRX算法用于原始高光谱图像，忽略了波段之间的高度相关性，从而产生了较多的虚警.而图7所示检测结果不理想是因为能量最大主成分中包含的异常目标信息相对于局部平均奇异度最大波段要小得多，甚至包含的很少，其主要包含的是背景能量信息.因而，在相同的检测阈值下，本文提出算法有明显的优势，证明了算法的有效性.

图7 SMIPCAFig.7 SMIPCA

为了更具体地说明本文提出算法的优越性，以高光谱图像检测到的目标个数、目标所占像素数、虚警所占像素数以及计算时间(单位为s)为指标对上述仿真结果进行比较，其比较结果如表1所示.

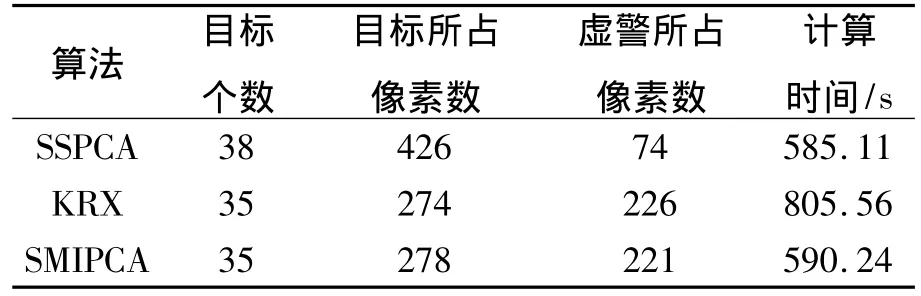
表1 算法性能比较Table 1 Algorithm performance comparison

从表格的数据中可明显看出，本文提出的算法可检测到较多的目标，具有较高的目标检测率和较低的虚警率，且节省了计算所用的时间，充分说明了本文算法的优越性能.

算法特性曲线用于描述不同检测阈值下检测概率Pd与虚警概率Pf之间的变化关系，提供算法检测性能的定量分析.将检测概率Pd定义为检测到的真实目标像素数目与地面真实目标像素数目的比值;虚警概率Pf定义为检测到的虚警像素数目同整幅图像像素数目总和的比值.通过考察检测到的异常点是否落入真实目标分布模板区域来判定检测到的是真实目标还是虚警.上述3种算法的特性曲线如图8所示，从图中可以看出本文提出算法较好地改进了KRX算法，具有良好的检测性能和较低的虚警率.

图8 算法特性曲线Fig.8 Algorithm characteristics curves

3 结束语

本文提出了一种基于选择性分段主成分分析与KRX算法相结合的异常目标检测算法.该算法充分利用了各波段子集内部较高的相关性，在有效降低数据维数的同时尽可能地保留了异常目标信息，并充分挖掘了数据的高阶统计信息，运用KRX算法对目标进行检测，达到了比较好的异常检测效果.

［1］童庆禧，张兵，郑兰芬.高光谱遥感——原理、技术与应用［M］.北京:高等教育出版社，2006:218-237.

［2］贺霖，潘泉，赵永强.基于波段子集特征融合的高光谱图像异常检测［J］.光子学报，2005，34(11):1752-1755.

HE Lin，PAN Quan，ZHAO Yongqiang.Anomaly detection based on feature fusion of band subset for hyperspectral image［J］.Acta Photonica Sinica，2005，34(11):1752-1755.

［3］张媛，何明一，梅少辉.基于主分量和独立成分分析的多光谱目标检测［J］.遥感技术与应用，2006，21(3):227-231.

ZHANG Yuan，HE Mingyi，MEI Shaohui.Target detection of multi-spectral image based on PCA and ICA［J］.Remote Sensing Technology and Application，2006，21(3):227-231.

［4］梅锋，赵春晖.基于空域滤波的核RX高光谱图像异常检测算法［J］.哈尔滨工程大学学报，2009，30(6):697-720.

MEI Feng，ZHAO Chunhui.Spatial filter based anomaly detection algorithm for hyperspectral imagery kernel RX detectors［J］.Journal of Harbin Engineering University，2009，30(6):697-720.

［5］GU Yanfeng，LIU Ying，ZHANG Ye.A selective kernel PCA algorithm for anomaly detection in hyperspectral imagery［J］.IEEE Trans Geosci Remote Sensing，2006，2(10): 725-728.

［6］赵春晖，王楠楠.基于背景抑制及顶点成分分析的高光谱异常小目标检测［J］.应用科技，2009，36(9):11-14.

ZHAO Chunhui，WANG Nannan.Anomaly detection of hyperspectral imagery based on background restrain and VCA［J］.Applied Science and Technology，2009，36(9):11-14.

［7］KWON H，NASRABADI N M.Hyperspectral anomaly detection using kernel RX-algorithm［C］//2004 International Conference on Iamge Processing.Singapore，2004:3331-3334.

［8］KWON H，NASRABADI N M.Kernel RX-algorithm:a nonlinear anomaly detector for hyperspectral imagery［J］.IEEE Trans Geosci Remote Sensing，2005，43(2):388-397.

［9］SCHOLKOPF B，SMOLA A J.Learning with kernels［M］.Cambridge:The MIT Press，2002:1-21.

［10］SCHOLKOPF B，SMOLA A J，MULLER D R.Kernel principal component analysis［J］.Neural Computation，1999，24(10):1299-131.