复杂信号环境下的GNSS定位星座选择算法

陈陌寒，郑 睿，王 云，陈 杰

(中国科学院微电子研究所 通信与多媒体SOC研究室，北京 100029)

在森林、高楼林立的城市等复杂环境中，多径和遮蔽效应会严重恶化某些GNSS(global navigation satellite system)卫星的测距精度，导致接收机定位精度严重下降.通过有效的星座选择算法从多颗可用于解算的卫星中检测并排除严重影响接收机定位精度的卫星是减小复杂信号环境中定位误差的一种有效途径，也是GNSS接收机的一个重要研究方向.

目前针对GNSS的选星方法主要基于GDOP (几何精度因子)选择最优定位星座，如最佳选星法［1-3］，模糊选星法［4］，加权 GDOP［5-6］，组合优选法［7］等.以上方法通过假设各颗卫星伪距测量误差相等或已知从多颗可见卫星中选择出几何分布最佳的卫星组合.但实际上，在复杂信号环境中各颗卫星的伪距测量误差实时变化且不可知，是影响接收机定位精度的主要因素，而基于GDOP最小原则的选星方法忽略了卫星伪距测量误差的影响，因此对定位精度改善有限.

另一类选星算法基于 RAIM(receiver autonomous integrety monitoring)算法.RAIM主要用于支持航空用户对卫星导航系统完好性检测［8］，应用于民用GNSS接收机时复杂度较高，需要对不同参数进行一系列限制［5，9-11］.

本文首先简要回顾了GNSS接收机最小二乘解算原理，推导了单颗卫星伪距测量误差和定位误差的线性关系;利用简化的距离残差平方和构造选星检验统计量，并证明该检验统计量可以反映单颗卫星伪距测量误差;给出了可应用于多颗卫星伪距测量错误时的选星方法.该方法通过了基于FPGA的GPS实时接收机仿真数据和真实数据的测试验证.测试表明该算法在复杂城市环境中能明显减小定位误差，长时间连续定点定位仿真测试中平均有效性超过80%，动态测试中有效性超过70%.同等条件下的对比测试表明，本文提出的选星算法的定位精度优于基于GDOP的选星算法.

1 复杂信号环境中的定位星座选择算法

1.1 最小二乘法解算原理

为了确定用户的三维位置(xu，yu，zu)和接收机时钟偏差tu，需要对至少4颗卫星的伪距进行测量.测量方程组为

式中:ρ为带噪声的测量伪距，j取1，2，…，n，n为观测方程个数即用于解算的卫星数目;s代表卫星在ECEF坐标系中的坐标，s代表用户在ECEF坐标系中的坐标，c为光速，tu代表接收机时与系统时的误差.将式(1)在近似位置点用泰勒级数展开，可以得到线性化的GNSS观测方程为［8］

式中:Δρ=［Δρ1Δρ2… Δρn］为n×1维向量，其元素是带噪声的测量伪距与基于线性化点预测的伪距之间的差值.为n×4维观测矩阵;ΔX=［ΔxuΔyuΔzu－cΔtu］T是4×1维向量，其元素是相对于线性化点的增量偏离，包括3个位置分量和接收机时钟偏差;ε为n×1维伪距测量误差矢量.

则ΔX的最小二乘估计值为

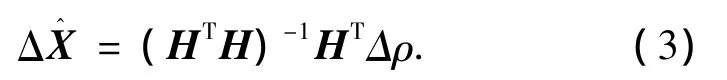
1.2 伪距测量误差和定位误差的关系

由ΔX的最小二乘估计值得位置误差矢量为

式中:伪距测量误差ε可同时包含随机和确定偏差项［8］.随机偏差项由观测噪声造成，假定观测噪声服从0均值、方差为σ2的正态分布N(0，σ2);确定偏差项由卫星轨道与星历预测轨道间的偏差以及多径等非公共(即独立)误差造成［8］，只影响正态分布的均值.第i个伪距存在确定偏差时对应伪距误差服从非0均值的正态分布εi～N(bi，σ2).

参考GPS标准定位服务的典型UERE预算［8］，随机偏差相对于确定偏差bi来说可被忽略，因此位置误差矢量和伪距测量误差的关系为

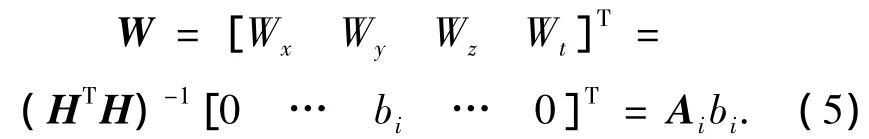
式中:A=(HTH)－1HT，Ai为矩阵A的第i列.

定义定位误差:

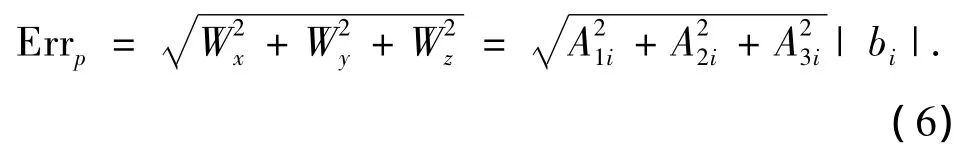
1.3 定位星座选择算法中检验统计量和定位误差的关系

求出ΔX的最小二乘估计值后，将其带入方程(2)的右端，把该结果与Δρ的测量值相比较，它们之间的差称为距离残差矢量:

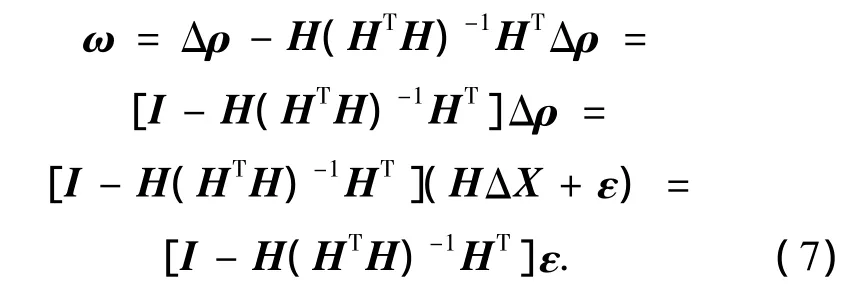
由于定位解算时至少需要4颗卫星，且通常情况下载噪比高的卫星伪距测量值更准确，本文提出的选星算法选取载噪比最大的4颗卫星作为预选卫星，检测并去除其余卫星所引入的错误的伪距测量量，设

并设

式中:Δρ'=［Δρmax5Δρmax6… Δρmaxn］为(n－4)×1维向量，其元素为不包含在预选卫星组合中的卫星在Δρ中对应的元素;

其中，H为(n－4)×4维观测矩阵，其元素为不包含在预选星座组合中的卫星在H中对应的元素;ε'为(n－4)×1维伪距测量误差矢量，其元素为不包含在预选星座组合中的卫星在ε中对应的元素.

定义星座选择算法的检验统计量为SISS(statistic indicator of satellite selection):

针对多颗卫星伪距测量值不准确的选星方法可以由针对单颗卫星测量值不准确的选星算法递归得到，因此假设伪距误差ε只考虑第i颗卫星的伪距偏差bi，则由SISS的定义可得

式中:Sii为矩阵S第i行第i列的元素.可见，SISS可以反映伪距测量误差，且由式(6)可知，伪距测量误差直接影响定位误差，因此SISS可以反映定位误差的大小.

1.4 定位星座选择算法的基本方法

以上分析假定所有卫星的观测噪声服从0均值、方差同为σ2的正态分布N(0，σ2)，但实际应用中并不能保证该假设成立，因此不能仅以SISS是否为0判断伪距测量值是否错误.本文提出一种针对工程应用的定位星座选择算法，可以检测并排除多个错误的伪距测量值，其算法步骤如下:

1)对所有可用于解算的卫星按载噪比大小进行排序，并选出载噪比最大的4颗卫星.

2)从余下的n－4颗卫星中依次挑出一颗卫星和步骤1)中的4颗卫星组合，计算SISS5，i(i=1，2，…，n－4)，将这n－4个检验统计量进行排序，如果SISS5，max＞N·SISS5，min(N的值一般由接收机性能根据经验选取)，则将SISS5，max对应的卫星视为影响定位结果的卫星，将其排除.而将SISS5，min对应的星座组合带入下一轮判断.

3)假设步骤2)共排除掉j1颗卫星(j1=0或1)，则从剩下的n－4－(j1+1)颗卫星中依次挑出一颗和步骤2)中 SISS5，min对应的星座组合，计算SISS6，i(i=1，2，…，n－4－(j1+1))，判断是否SISS6，max＞N·SISS6，min(N的值一般由接收机性能根据经验选取)，如果是则将SISS6，min对应的卫星视为影响定位结果的卫星，将其排除.而将SISS6，min对应的星座组合带入下一轮判断.

4)重复步骤3)直到n－4－(j1+1)－(j2+1)－…－(jm+1)=0(m≤n－4).

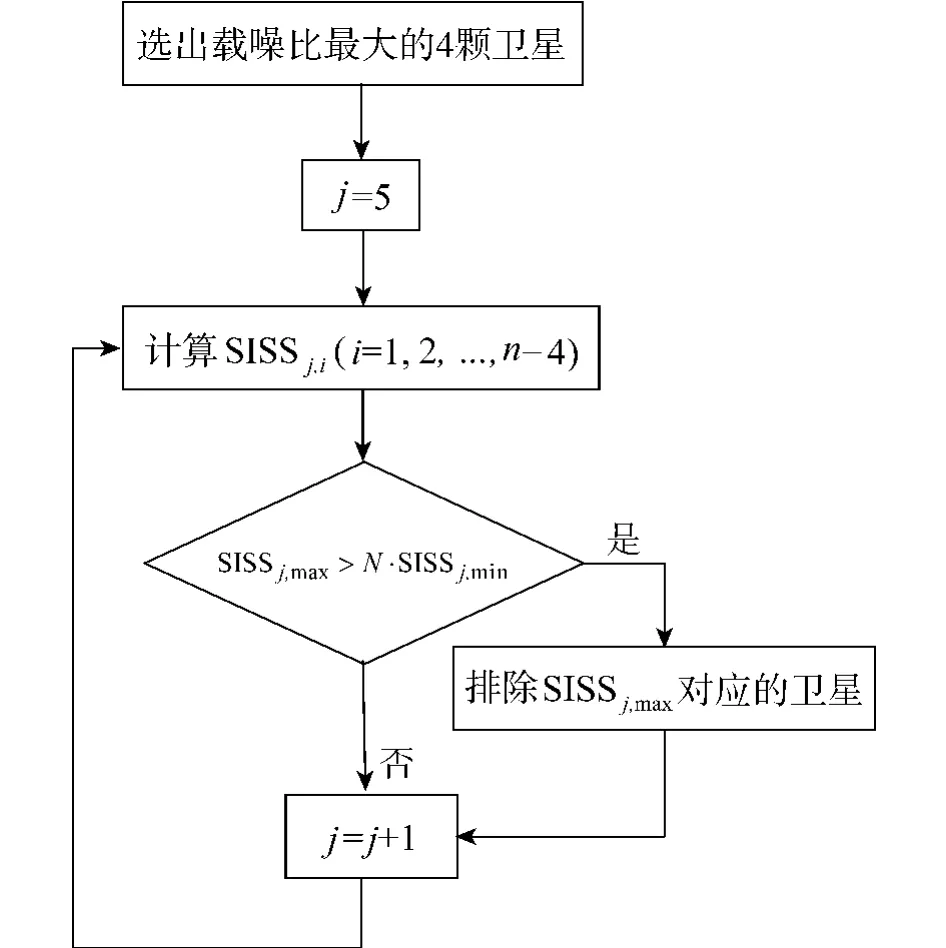
图1 选星方法流程图Fig.1 Flow chart of satellite selection method proposed

表1 计算量分析(FLOPS)Table 1 Computation load comparison for different n

2 仿真验证

2.1 试验环境

利用本实验室自主知识产权的手持设备专用GPS基带处理芯片开发平台对本文提出算法的定位性能进行测试.该平台包括ARM9处理器及基带信号处理协处理器.GPS信号的捕获、跟踪、同步和解调电文由协处理器完成，定位解算由ARM完成，定位结果通过RS232接口传入PC，进而利用Matlab进行统计分析.

2.2 定位星座选择算法的定位性能

2.2.1 静态测试

首先利用GPS信号验证本算法对GNSS接收机静态定点定位误差的影响，使用 SprintR STR4500GPS信号发生器提供的24 h定点定位场景进行10 000 s仿真实验，产生50～200 m(参考多径和无主径效应可能造成的伪距误差值［8］)之间的随机值作为任一卫星的测距误差.该定点在WGS－84坐标系下的三维坐标为(4 063 656.11，－255 466.33，4 892 925.42).设经过选星算法处理后定位误差减小的定位点个数与定位点总数的比值为选星算法的“有效性”.分析10 000 s静态仿真数据发现，使用组合优选法后，有效性为46.04%;而使用本文提出的选星算法后共有8 067次成功排除增加了伪距误差的卫星从而减小定位误差，平均有效性达到80.67%;共有1 933次定位精度未提高，这是由于增加了伪距误差的卫星在4颗预选卫星内，因而未被检测出.图2的统计数据柱形图显示了伪距误差和选星算法有效性之间的具体关系，选星算法的有效性随着伪距误差的增大而提高.表2为静态定位误差分析.本文提出的选星算法将三维定位误差均方根由未采用选星算法时的 43.44 m减小至6.47 m，对定位精度的改善优于组合优选法.

表2 静态定位误差分析Table 2 Position errors in static tests

图2 选星算法有效性分析Fig.2 Availability for different range errors

2.2.2 动态测试

为验证本算法对GNSS接收机动态定位误差的影响，采用2008年10月15日北京市二环路北段实际路测数据，道路周围高楼密集，具有一定代表性.由于高楼引起信号被阻挡和反射，使得定位点出现了几次跳跃和中断.图3为局部轨迹放大定位对比图，图4为图3在GoogleEarth地图上的映射.在高楼密集处，未经过选星处理的定位点偏差明显，经过本文提出的选星算法处理后的定位结果更接近接收机实际运动轨迹.本文算法对定位精度的改善优于组合优选法.

图3 局部定位轨迹对比图Fig.3 Position estimates using different algorithmspart of the route

分析1 000 s实际路测定位结果值发现，共有63个定位点的定位误差大于20 m，其中有46次经过选星算法处理后的定位误差明显减小，有效性达到73.01%，17次和未经过选星算法处理时的定位结果一致，主要由于遮挡和多径效应造成出现测距误差的卫星在预选卫星内，导致选星算法无法将其检测进而排除.

图4 GoogleEarth地图上局部定位轨迹对比图Fig.4 Position estimates using different algorithms-part of the route on GoogleEarth

3 结束语

为减小GNSS接收机在复杂环境中的定位误差，本文提出了一种有效的定位星座选择算法.该选星算法性能优于传统基于GDOP的选星算法，能够有效提高静态定位和动态定位的定位精度.测试表明该选星算法在复杂城市环境中可以有效检测出并排除掉伪距测量值错误的卫星进而减小错误定位点出现的概率;长时间连续定点定位仿真测试中平均有效性达到80.67%，动态测试中达到73.01%，显著减小了GNSS接收机在复杂环境下的定位误差.但是多径影响会令载噪比较大的卫星产生测距误差，此时仅使用本文提出的选星算法效果有限.后续研究将着重解决该问题

［1］PHATAK M S.Recursive method for optimum GPS satellite selection［J］.IEEE Transactions on Aerospace and Electronic System，2001，37(2):751-754.

［2］刘会杰，张乃通.基于GDOP的最优定位星座性能研究［J］.高技术通讯，2000，10(1):43-47.

LIU Huijie，ZHANG Naitong.Performance research for GDOP based optimum positioning constellation［J］.High Technology Letters，2000，10(1):43-47.

［3］张贵明，黄顺吉.一种新的GPS导航卫星选择算法［J］.电子科技大学学报，2000，29(3):221-224.

ZHANG Guiming，HUANG Shunji.A new satellite selection algorithm for GPS navigation［J］.Journal of University of Electronic Science and Technology of China，2000，29 (3):221-224.

［4］张超，陈天麒.GPS中的一种新的选星方法［J］.实验科学与技术，2006，4(2):25-27.

ZHANG Chao，CHEN Tianqi.A new selecting-star algorithm in GPS［J］.Experiment Science and Technology，2006，4(2):25-27.

［5］SAIRO H，AKOPIAN D，TAKALA J.Weighted dilution of precision as quality measure in satellite position［J］.IEE Proc-Radar Sonar Naving，2003，150(6):430-436.

［6］KIHARA M.Study of a GPS satellite selection policy to improve positioning accuracy［C］//IEEE Position Location and Navigation Symposium.Las Vegas，1994:267-273.

［7］张强，张晓林，李宏伟，等.组合卫星接收机中的选星算法［J］.北京航空航天大学学报，2007，33(12):1424-1427.

ZHANG Qiang，ZHANG Xiaolin，LI Hongwei，et al.Satellite selection algorithm for combined receivers［J］.Journal of Beijing University of Aeronautics and Astronatics，2007 33(12):1424-1427.

［8］KAPLAN E D，HEGARTY C J.Understanding GPS principles and applications［M］.London:Artech House，1996: 258-268.

［9］KUUSNIEMI H，LACHAPELLE G.Position and velocity reliability testing in degraded GPS signal environments［J］.GPS Solution，2004，8:226-237.

［10］DIGGELEN F D，BROWN A.Mathematical aspects of GPS RAIM［C］//IEEE Position Location and Navigation Symposium.Las Vegas，1994:733-738.

［11］MACGOUGAN G D.High sensitivity GPS performance analysis in degraded signal environments［D］.Calgary:The University of Calgary，2003:52-74.

［12］PARKINSON B W，SPILKER J J，Jr.Global positioning system:theory＆applications［M］.Washington，DC:A-merican Institute of Aeronautics and Astronautics，1996: 190-207.