基于混沌与DFT对无人机控制不稳定性的研究

刘利钊，张天华，胡晓京，李茂青

(1.厦门大学信息科学与技术学院自动化系，福建厦门361005;2.路易斯安那理工大学电子工程学院电子信息工程系，路易斯安那州罗斯顿70112)

直升机作为集成了现代最新科技的旋翼型飞行器应用广泛，机载控制系统和地面控制系统的信息化发展增强了直升机的飞行稳定性和可控性［1-4］，减少了其在执行任务时的失事概率.但同时这也使直升机成为了复杂的旋翼型信息化空中平台:机体构造与机载系统融为一体;整体结构参数愈趋繁复;运动特征愈趋多变，而且在特定的情况下［5］会产生不稳定现象.新加坡国立大学陈本美教授和其无人机团队在无人直升机控制方面取得了很多重要的成果.以无人驾驶直升机为实验对象，并通过对陈本美教授及其他无人机团队遇到的若干次坠机事件［6-8］的分析发现:直升机系统本身应该是一个内随机系统，它在某些飞行状态会出现不稳定现象;经典的直升机非线性模型是一个内随机模型，参数的某些搭配可能导致模型运动曲线的发散;辨识模型对某些信号的不敏感或者误判是飞机自动控制系统不稳定乃至易失控的原因之一，模型辨识中运用DFT算法对某些高次谐波的人为省略则是使辨识模型与实际系统发生偏离的重要原因.

1 经典的无人直升机运动模型与模型辨识技术

1.1 直升机飞行运动模型

经典直升机非线性运动模型如下:

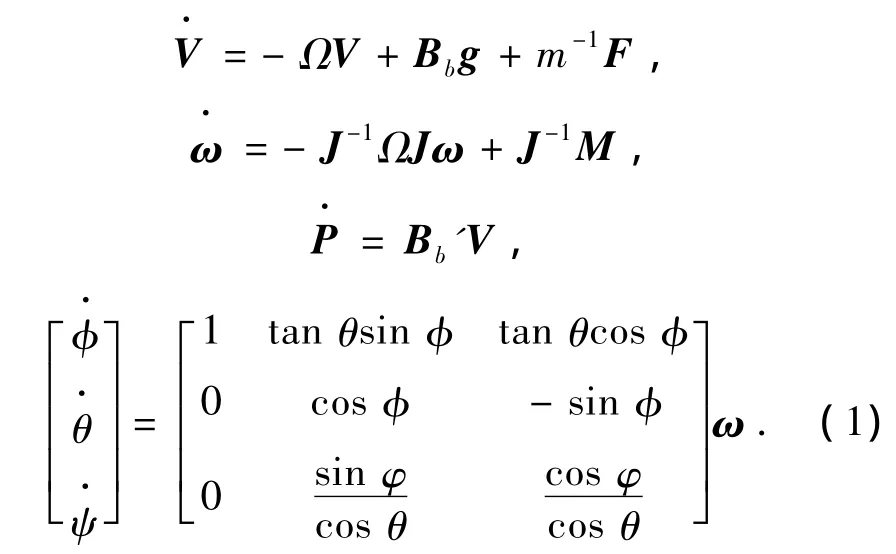
1.2 模型辨识与直升机偏航模型

给定无人直升机控制系统如图1所示［9－10］.

图1 直升机控制系统Fig.1 Helicopter control system

下文中用δpedal表示直升机偏航输入量，ωz代表直升机在Z平面内角速度.把计算系统、伺服系统和直升机运动系统看做整体偏航系统，该偏航模型的传递函数表示形式为

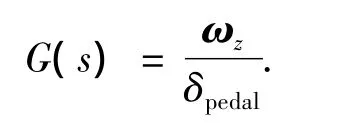
将若干组正弦、阶梯、随机、脉冲样本信号作为输入信号，测试并记录输出的ωz，抽样过程中尽量使抽样频率T→Tmin，DFT变换保留前三阶谐波.

2 波动信息能量函数

定义1 对于任何一个给定函数f(t)频域对应函数f(s)，可以将其表示为，其中f(si)为连续可导函数，那么该函数的波动信息能量变换为

波动信息能量比为

物理含义:波动信息能量函数代表某一给定样本信号在选定频域内的波动信息所具有的能量总和.波动信息能量比表示该信号某一频率的后段高频能量与总能量的比值.

定义2 设某系统的物理传递函数为W(S)，辨识传递函数为G(S)，{S1，S2…Sn}为试验样本集，若

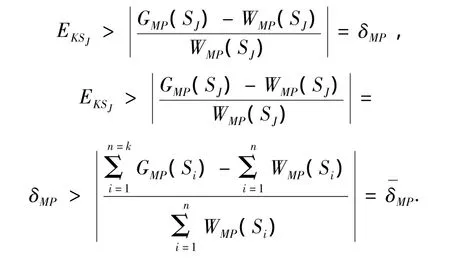
式中:δMP为幅频、相频拟合偏差比，则为幅频、相频平均拟合偏差比.

3 DFT信息能量的不稳定性分析

对于离散信号x(n)，长度为N来说，DFT变换:

DFT反变换:

又可以表示为

对于高次谐波:

一般情况下DFT和FFT变换只保留除主波值以外的二、三阶谐波.X(n)的2种信息能量变换为

式中:

对于不同频率不同波动程度的函数能量比较如图2.可见信号的在住谐波能量确定的情况下，高次谐波所具有的信息能量与其波动程度成正比.

假设抽样周期为T，离散化信号长度为n.给指定无人直升机系统输入一周期1 s，幅值0.2单位，初始相位π/4的正弦样本信号［11-12］:

图2 不同函数波动能量对比Fig.2 Comparison of different wave energy function

该信号时域、幅频特性如图3，图中k=3代表1 Hz波动信息能量为

当ni－ni－1=nj－nj－1，i≠j＜n，k=3，K→∞时，

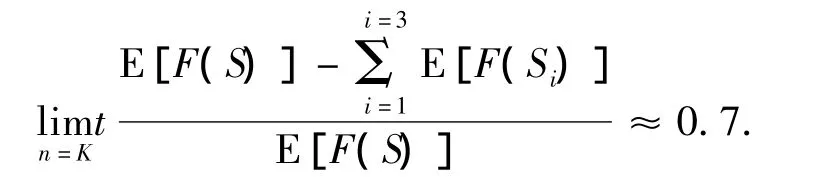
该正弦样本信号经过DFT变换并保留主谐波后，将导致原信号波动信息能量大幅减少.

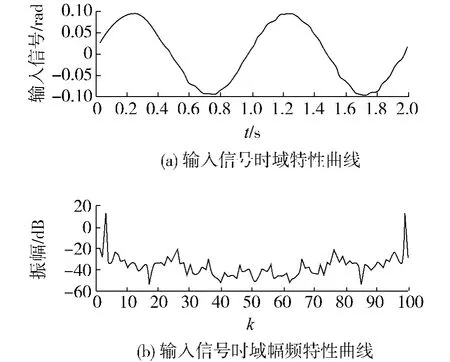
图3 初始相位π/4正弦样本信号Fig.3 The initial phase of sinusoidal signal samples

信号响应输出如图4，图中k=3代表1 Hz.k= 5，8，36，44，60，82，85，90时，幅频曲线波动明显且信号运动趋势发生偏转.

该试验系统对信号高频部分的整体敏感度不高.但如果输入信号在输入输出反映剧烈的频率点上丢失信息或者存在信息偏差，将可能造成幅频曲线的剧烈震动，同时也有可能造成相频曲线和时域特性曲线的大幅偏移.对于确定系统来说此高阶部分能量影响甚微，但对于随机系统来说，高次谐波的偏转可能导致系统内相关参数的剧变或者耦合，从而影响整个系统的运动性能和轨道.

图4 相位π/4样本信号输出响应Fig.4 The signal output response of π/4 phase samples

通过对某一无人直升机系统连续输入20个0.5～10 Hz的正弦波、阶梯波、随机波等样本信号，获得如下辨识模型［13-14］:

该模型与实际系统的幅频和相频特性比较如图5所示.取试验样本集{S1=0，S2=0.001…Sn=100}，其中Sj－Sj－1=0.001，假设抽样周期为0.000 01 s，DFT变换保留前3项，则

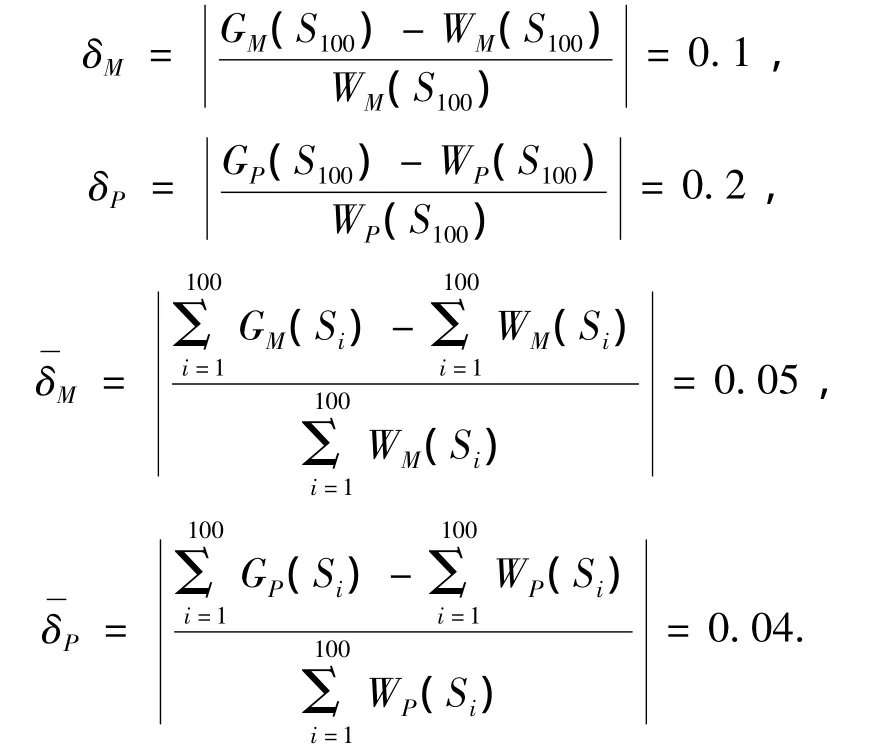
EKSJ≈0.7＞δP=0.2＞δM=0.1.根据定义2:δM＞，判定该辨识模型在某些高阶信号处的幅频-相频将发生大幅偏转和反向运动，并在时域范围内展示为剧烈抖动和逆向输出.

根据拟合信号可以发现模型在低频部分0.1～0.5 Hz的幅频和相频均跟随较好;幅频曲线从0.5～5 Hz开始发生分离，同时相频曲线跟随较好;幅频曲线和相频曲线从5～10 Hz内均发生偏离，其中2条幅频曲线运动趋势相同，相频曲线运动趋势相悖.

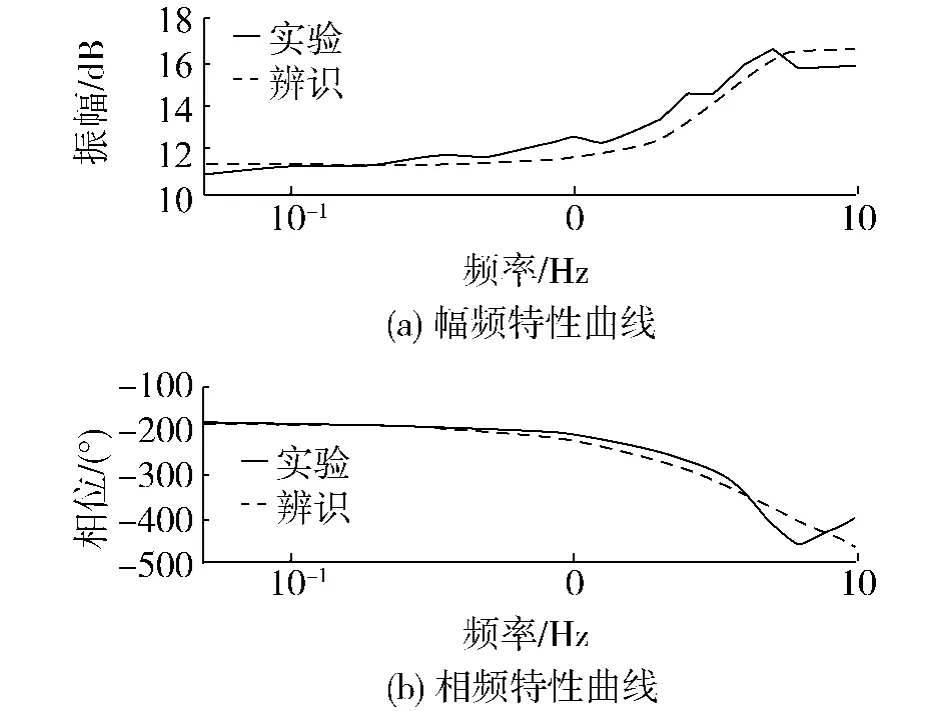
图5 辨识模型与实际幅频输出响应比较Fig.5 Amplitude-frequency output response comparison between identification model and actual model

该模型时域输出如图6中所示，0.5 Hz的正弦信号拟合完好;1 Hz的正弦信号在1.6 s、1.75 s、2.2 s、2.3 s、2.4 s等位置出现与原信号反趋势的运动［15-18］.

图6 辨识模型与实际时域输出响应比较Fig.6 Comparison of identification model and the actual output response in time

从以上可以看出DFT变换省略的高次谐波可能导致系统模型对某些频率信号的输出反应出现较大误差或发生逆转［15，19］.

4 Shilnikov标准速度方程

直升机非线性系统宏观稳定，内随机区域可能存在于:速度、角速度、动力与飞机自身结构存在综合函数关系，若经典非线性运动方程组中任何一个方程出现混沌，则该方程组将出现混沌;速度与角速度均受另外2个参数和时间的直接影响，可能导致速度与角速度无法实时同步与协调;需要各个参数达到某一特定值时，参数间可能出现矛盾或无法按照预设的轨道变换.这些都可能导致该模型的不稳定、锁死或者出现混沌失控现象.

在速度方程中，角速度矩阵Ωx=ω×x，其中，

直升机惯性矩阵J可展开为

传输矩阵Bb可展开为

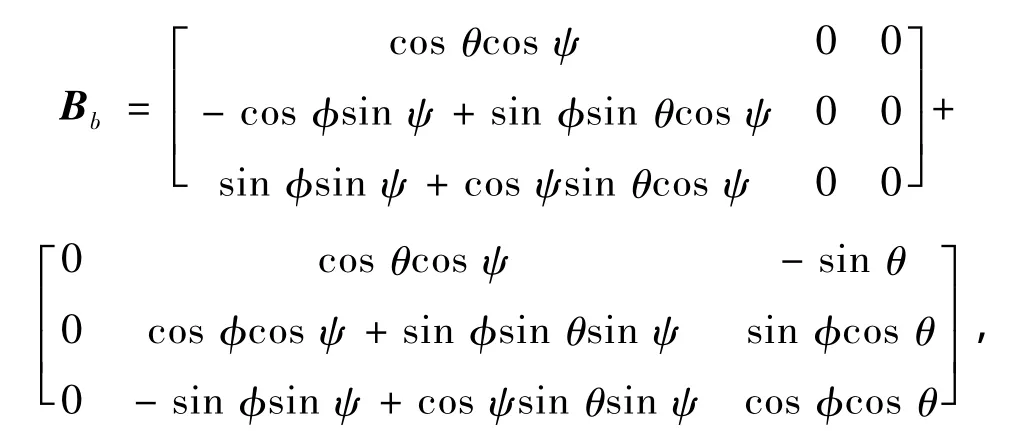
Cv0=g·Bb在速度方程中可视为可变换常数矩阵.式中:

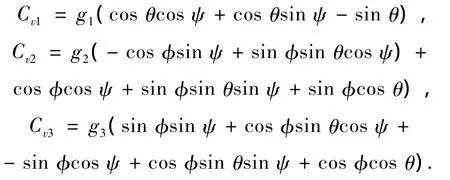
力向量F=Fm+Ft+Ff.

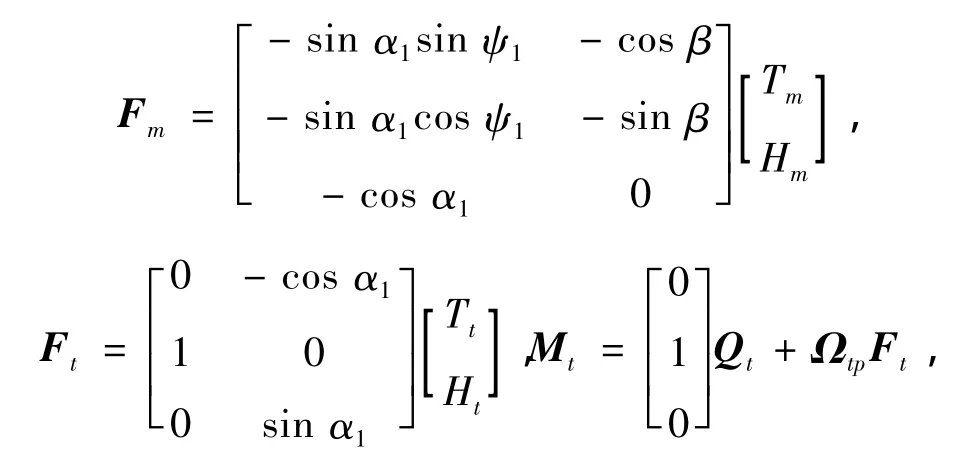
力矩向量M=Mm+Mt+Mf，

可得直升机合力与速度、角速度和位置的函数关系:

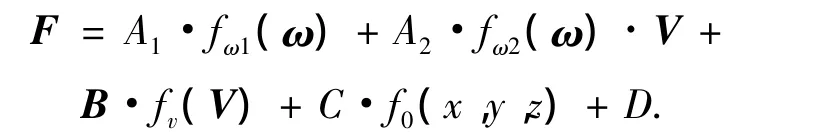
将其带入原速度方程(1)可得

整理可得Shilnikov标准速度方程［17－18］:

同理可得Shilnikov标准速度方程:

常数项C不影响该方程的不稳定性.接下来以速度方程为分析对象来说明其具有不稳定性和混沌特征.

5 非线性速度方程的不稳定分析与混沌特征

设(V1，V2，V3)为非线性速度方程V·=Aω·V+ Bv·F(V)+Cv的解空间，该方程有可能有多个平衡点.限于篇幅暂寻找几个以说明其混沌特性［16，22］.当Aω=Ω且

Fm1+Ft1+Ff1=0，Fm3+Ft3+Ff3=0时，

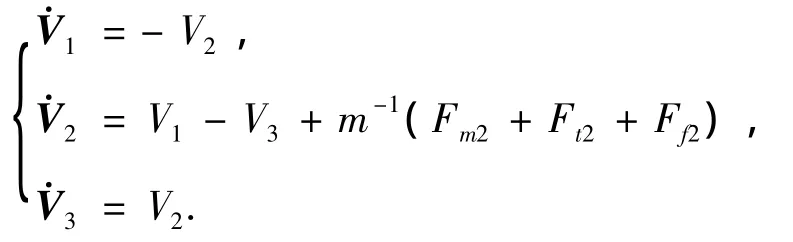
Fm1+Ft2+Ff3为饱和函数时，该方程如下:

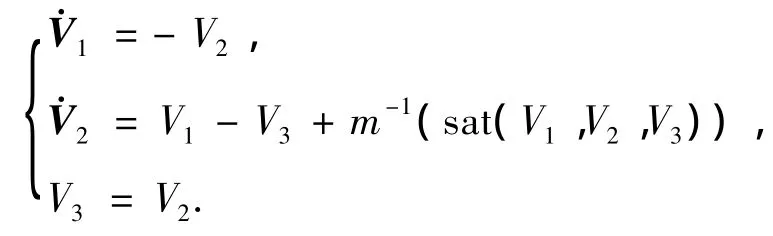
该方程有平衡点:

系统具有3个平衡点:V1=(－m－1，0，0)，V2= (0，0，0)，V3=(m－1，0，0).当V1≥k时，V1=－m－1，V1平衡点稳定;当V1≤－k时，V1=m－1，V3平衡点稳定;当k≥V1≥－k时，若k=－m－1，V1为任意值;若k≠－m－1，V1=0，V2平衡点不稳定.

当该三阶非线性速度方程参数配置如上时，该系统出现混沌的条件如下:

1)在平衡点V1和V3处的Jacobian矩阵的特征值δi±jωi、γi，i=1，2，满足如下条件:|γi|＞|δi|＞0，δ1δ2＞0;V1、V3为鞍焦点.

2)V1、V2、V3位于同一条空间直线上，存在异宿轨道.

6 非线性速度方程的混沌仿真

根据Shilnikov定理［17-18］，直升机非线性速度方程可以产生混沌.

取系统(1)的矩阵Aω=Ω中的参数为wz=wy= wx=－0.9，当Bω=0时系统的平衡点位于(0，0，0)，系统特征值为－0.098 3，0.156 4+0.739 8i，0.156 4－0.739 8i，该平衡点稳定但系统不会进入混沌.选取系统的初始值为(0.3，0.14，0.13)，Bω= BΔ则系统的状态变量V1、V3的相平面图如图7所示，可以看出明显的混沌现象.

图7 非线性史尼科夫混沌仿真Fig.7 Shilnikov nonlinear chaos simulation

7 R-REFRLEX仿真

选取试验机型为雷虎－90型标准机型，如图8左，同时该机型与新家坡国立大学无人机课题组的试验机型相同，可以印证他们控制过程中发生失控的原因.自动控制部分选择不易发生电磁干扰和混沌同心干扰的DIAMOND集成系统，该系统从以往的试验和结论表明［23-24］，可以Din1xy≈Din1xymin，Dout1xy≈Dout1xymin，从而在仿真过程中忽略控制系统对无人直升机系统稳定性造成的影响.其系统结构如图8右所示.

图8 无人直升机系统集成结构图Fig.8 Integration structure of UAV systems

采用飞鼠无人机地面控制软件，设定无人直升机按照回型封闭航线进行飞行.如图9所示，在飞行过程中始终调整速度方程F(V)+Cv中的参数Aω=Ω.变换角速度矩阵Ω=中角速度值，同时随机变换V向量值，在变换中尽量使V与w独立，从而满足Shilnikov定理，并使原方程中V与w的解空间内某一子集中的所有解组合都出现在飞行状态中.

仿真结果如图10所示，无人直升机的飞行路线用细线条表示，在变换V与w的过程中，大多数情况下系统处于正常状态.但粗黑线条所标出的路线却极不稳定，而且多次出现事故.说明在Aω=Ω的条件下，V与w在某值域内的组合会使无人直升机系统进入不稳定或者混沌状态［25］，从而导致失控.

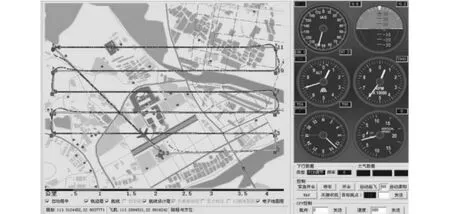
图9 直升机封闭路线飞行仿真Fig.9 Simulation of helicopter flight in closed line

图10 无人机封闭路线混沌仿真Fig.10 Simulation of UAV chaos in closed line

8 结束语

通过仿真可以看出无人机非线性模型所描述的运动系统确实具有不稳定性，DFT算法所带来的负面影响不可忽略;在选定无人机非线性运动方程的部分初始条件下，连续尝试其解空间的解组合可以搜索到原方程的不稳定区域或者系统的内随机区域.这也就说明了无人机在长时间内连续执行不同任务时所产生的不稳定性，进而证明了运用DFT算法辨识出来的系统模型来控制具有非线性运动特征的无人机系统会产生不稳定、或在特定情况下进入混沌的极大可能性.这将为解释无人机失控乃至有人驾驶飞机失控的现象提供一个思路，从而针对失控现象的构成因素谋划应对策略与技术改进.但是目前在飞行仿真中只能记录航点数据，无法确切记录每一个航点上无人机的具体状态数据，这给验证飞行仿真数据与MATLAB仿真数据之间的对应关系制造了障碍，从而无法找到原方程的所有不稳定区域，而只能通过特例来寻找某些特殊的不稳定点.这部分将是接下来要解决的问题.

［1］METTLER B.Identification modeling and characteristics of miniature rotorcraft［M］.New York:Kluwer Academic Publishers，2003:225-228.

［2］PROUTY RW.Helicopter performance，stability，and control［M］.Malabar:Robert Krieger Publishing Company，1990:155-158.

［3］SHIM D H，KIM H J，SASTRY S.Control system design for rotorcraft-based unmanned aerial vehicle using time-domain system identification［C］//Proc of 2000 IEEE International Conferenceon ControlApplications.Anchorage，USA，2000:808-813.

［4］SUGENO M，HIRANO I，NAKAMURA S，et al.Development of an intelligent unmanned helicopter［C］//Proc of 1995 IEEE International Conference on Fuzzy Systems.Yokohama，Japan，1995:33-34.

［5］LIU L Z，LIU Y C，HUANG Z L，et al.The chaotic disturbance of UAV system＇s communication and coping strategy［C］//ICCCAS08 Proceedings.Xiaman，China，2008:155-160.

［6］CAI G W，PENG K M，CHEN B M，et al.Design and assembling of a UAV helicopter system［C］//Proc of 5th International Conference on Control＆Automation.Budapest，Hungary，2005:697-702.

［7］CHEN B M，LEE T H，PENG K M，et al.Hard disk drive servo systems［M］.London:Springer，2006:112-118.

［8］HE Y，CHEN B M WU C.Composite nonlinear control with state and measurement feedback for general multivariable systems with input saturation［J］.Systems＆Control Letters，2009，54:455-469.

［9］CAI G W，CHEN B M，PENG K M，et al.Modeling and control system design for a UAV helicopter［C］//MED06 Proceedings.Ancona，Italy，2006:132-137.

［10］STEVENS B L，LEWIS F L.Aircraft control and simulation［M］.2nd ed.Hopoken:John Wiley＆Sons，2003:87-92.

［11］PENG K M，CAI G W，CHEN B M，et al.Comprehensive modeling and control of the yaw dynamics of a UAV helicopter［C］//Proceedings of the 25th Chinese Control Conference.Harbin，China，2006:316-322.

［12］METTLER B.Modeling small-scale unmanned rotorcraft for advanced flight control design［D］.Pittsburgh:Carnegie Mellon University，2001:46-47.

［13］刘利钊，张天华，刘英超，等.无人控制系统的边缘失控研究与建［C］//CPCC2008会议论文集.北京，2008:57-60.

LIU Lizhao，ZHANG Tianhua，LIU Yingchao，et al.Research and modeling of edge out-of-control on unmanned system［C］//CPCC2008 Conference Proceedings.Beijing，China，2008:57-60.

［14］刘利钊，张天华，胡晓京，等.无人控制飞行器的模型细化与混沌控制［J］.仪器仪表学报，2008(4):120-124.

LIU Lizhao，ZHANG Tianhua，HU Xiaojin，et al.Unmanned aircraft model refinement and chaos control［J］.Scientific Instrument，2008(4):120-124.

［15］刘彬，谢平.一种实序列FFT的新算法［J］.燕山大学学报，1997，21(2):11-15.

LIU Bin，XIE Ping.A new algorithm for real valued sequence of FFT［J］.Journal of Yanshan University，1997，21(2):11-15.

［16］PECORA L M，CARROLL T L.Driving systems with chaotic signals［J］.Phys Rev Lett，1991，44(4):23-74.

［17］KOCARE L，PARLITZ U.General approach for chaotic synchronization with applications to communication［J］.Phys Rev Lett，1995，74(25):5028-5046.

［18］TOKUDA I，TAMURA A，TOKUNAGE R，et al.Learning algorithm for chaotic dynamical systems which solve optimization problems［J］.IEICE Trans，1998，81:377-388.

［19］孙福玉.傅里叶变换与拉普拉斯变换关系的可视化分析［J］.赤峰学院学报:自然科学版，2007，23(1):36-40.

SUN Fuyu.Visual analysis of the relationship between Fourier transform and Laplace transform［J］.Journal of Chifeng College Natural Science Edition，2007，23(1): 36-40.

［20］王茂海，刘会金，彭辉，等.采样信号频率偏离设计值情况下离散傅立叶变换的误差分析［J］.电测与仪表，2001，38(1):22-26.

WANG Maohai，LIU Huijin，PENG Hui，et al.Analysis on errors of discrete Fourier transform(DFT)in case of signal frequency drifting from designed value［J］.Electrical Measurement＆Instrumentation，2001，38(1):22-26.

［21］SILVA C P.Shilnikov＇s theorem_A tutorial［J］.IEEE Transactions on Circuits and Systems_I:Fundamental Theory and Applications，1993，40(10):32-37.

［22］王平，冯勇，孙黎霞，等.线性系统通过非线性反馈产生的混沌现象［J］.自动化技术与应用，2002，21(5):4-6.

WANG Ping，FENG Yang，SUN Lixia，et al.Chaos caused by linear systems through nonlinear feedback［J］.Automation Technology and Application，2002，21(5):4-6.

［23］LIU L Z.The chaotic characters and new control strategy of unmanned airplane information system［C］//International Symposium on Computational Intelligence and Design 2008 Proceedings.Xiamen，China，2008:120-123.

［24］PERRY F W，MARK T，M，ADAMS J W.Techniques for measuring the electromagnetic shielding effectiveness of materials:Part I:far-field source simulation［J］.IEEE Transactions on Electromagnetic Compatibility，1988，30 (3):239-250.

［25］GREENE K.Hidden in disorder:chaos-encrypted information goes the distance［J］.Science News，2005，168 (21):325.