二维传播算子DOA估计的改进算法

刁 鸣，陈 超，杨丽丽

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

目前，在阵列信号处理领域，对二维波达方向估计方法的研究已经涌现了很多的成果，传统的二维MUSIC算法需要在整个参数平面上进行谱峰搜索，计算量巨大，难以应用于工程实际，ESPRIT方法不需谱峰搜索，与MUSIC方法相比，具有较好的实时性，但是它存在一个参数配对的问题.文献［1］提出的DOA矩阵法可以避免谱峰搜索而直接计算出二维DOA参数，且参数能自动匹配，在一定程度上解决了上述问题，但存在相位模糊;文献［2］提出的基于L型阵列的波达方向估计算法，无相位模糊，解决了信号方位角和俯仰角的配对问题，但需计算多个相关矩阵后再对大矩阵进行特征分解，计算量仍很大;文献［3］基于双平行线阵列的特点，对子阵进行合并求解，使得协方差矩阵中不再含有冗余数据，但仍不可避免协方差矩阵特征分解带来的复杂计算.传播算子算法［4］利用线性运算代替特征分解，在解决计算量问题上有着巨大优势.文献［5］中Tayem等人提出的一种基于双L阵的二维DOA估计的传播算子算法，为了提高估计精度，需要进行2次方位角估计，文献［6］采用了空间三平行线阵列结构的传播算子算法，以增加一条均匀线阵来提高算法的估计精度.本文将数据共轭重排［7］的思想引入到传播算子算法，基于双平行线的阵列结构，提出一种改进的传播算子二维DOA估计方法，该方法在不增加计算量和阵元数的前提下，通过接收数据的共轭重排再利用，可以减少信源间的相关性，并且提高算法在快拍数有限及低信噪比条件下的估计性能.

1 阵列结构和信号模型

阵列结构由如图1所示的2个平行均匀线阵构成.其中，以位于原点的阵元为参考点，Y轴上共有M+1个阵元，前M个阵元组成子阵列L1，后M个阵元组成子阵列L2，X-Y平面上的M个阵元组成子阵列L3，且X轴方向和Y轴方向的阵元间距均为d，d的取值为1/2信号波长.

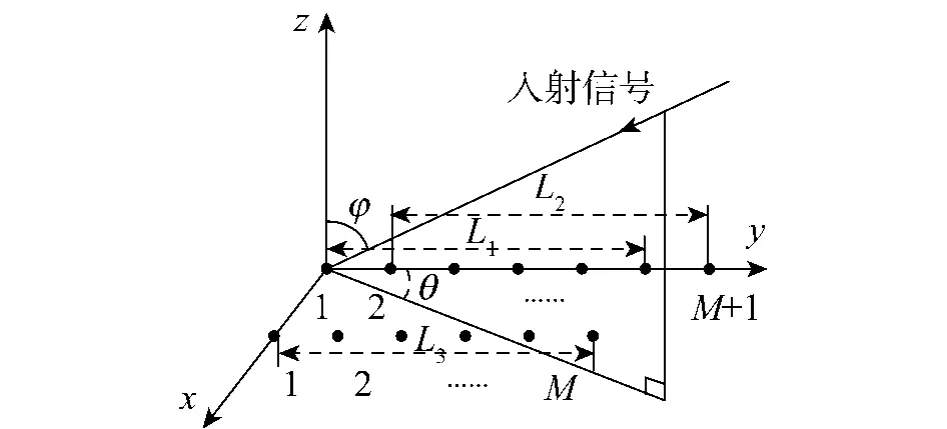
图1 双平行线阵的阵列结构Fig.1 Structure of two parallel ULAs

假设空间有D个同中心频率的远场窄带信号入射到天线阵上，第i个入射信号的方位角和俯仰角分别为θi和φi(i=1，2，…，D)，各阵元输出的噪声是统计独立、均值为0、方差为σ2的加性高斯白噪声，噪声与信号不相关.则L1、L2、L3接收到的信号分别表示为

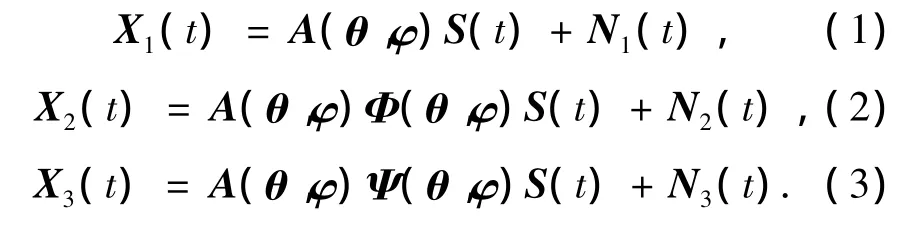
式中:

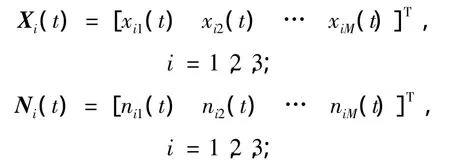
式中:λ为波长，d为天线阵列中2个相邻阵元的距离，Xi(t)和Ni(t)分别为第i个子阵列在第t个快拍时刻的接收数据和接收到的噪声数据.这样Φ(θ，φ)和Ψ(θ，φ)分别反映了子阵列L2和子阵列L3相对于子阵列L1的旋转不变关系.

2 改进算法的原理及性能分析

不考虑噪声影响，将X1、X2、X3按式(4)所示构造矩阵X:

将A和C分别进行分块处理:

式中:

假设C1为非奇异矩阵，即C1的D行互相独立，那么C2是C1的线性变换，有

式中:P定义为传播算子，P的求解需要信源方位信息，可以由空间协方差矩阵求解传播算子的估计值.

对Rx进行分块处理:Rx=［Rx1，Rx2］，其中，Rx1、Rx2的维数分别为3M×D和3M×(3M－D).由式(7)易推得

由于噪声的影响，使数据模型和实际情况有所偏差，因此，式(9)不能严格相等，可通过最小化求得传播算子的估计值.

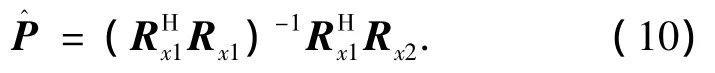
为进一步提高估计性能，将接收数据共轭重排的思想推广到传播算子算法的二维DOA估计中，提出传播算子算法的二维DOA估计改进算法.

式中:JM代表副对角线上元素为1，其余元素均为0的M阶方阵.可见，Rx和Rx均可以划分成9个M×M维的子矩阵，将这些子矩阵按式(12)进行重排相加求平均:

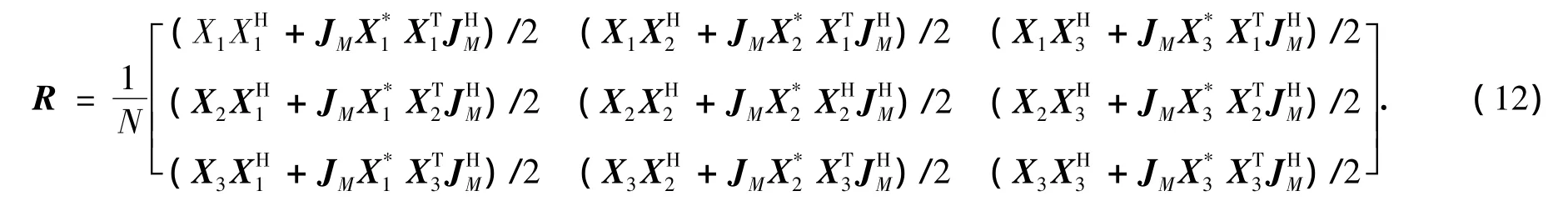
观察矩阵R中的第1个M×M维子矩阵:

式中:

对于独立的信号源，协方差矩阵RS应为实对角阵，即RS=，又根据Q*，R，QT3个对角阵相乘可交换顺序进行计算，并且Q*QT=I，可以推导出:

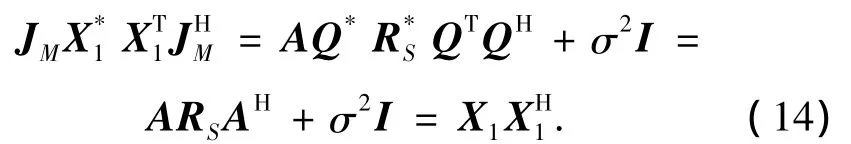
同理可推得矩阵R中9个M×M维子矩阵的2个相加项分别相等，因此，利用Rx估计传播算子和利用R估计传播算子应得到相同的.由于R将接收数据共轭重排再利用了一次，使协方差矩阵的估计更准确，当信噪比较低，快拍数较少时，使用R进行估计可以获得比Rx更好的性能.

式中:P1，P3，P5的维数与A2的维数相同，P2，P4的维数与A1的维数相同.根据式(5)～(7)可得

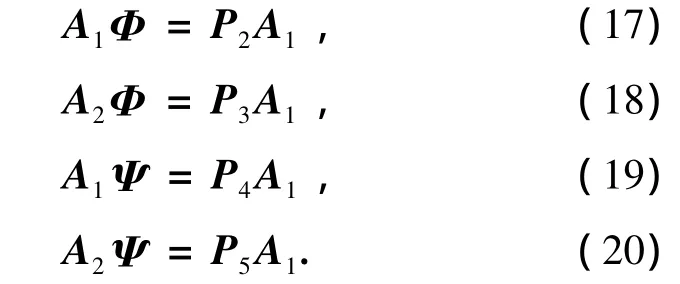
由式(17)、(19)可知，Φ和Ψ的对角线元素分别对应于P2、P4的特征值.在实际情况中，对P2和P4的特征分解是分别进行的，因此不能保证其特征值是一一对应的，在此可以采用快速配对算法［8］来解决参数配对问题.对P2进行特征分解得到其D个特征值分别为［λ1λ2… λD］，相应的特征向量分别为W=［w1w2… wD］，与P2的第i个特征值λi相对应的P4的特征值λi'应为

式中:yik是矩阵Y第i个列向量yi的第k个元素.

由此可得，Φ和Ψ的对角线上第i个元素分别为λi和λi'，结合Φ和Ψ的表达式，可以估计入射信号的方位角和俯仰角分别为

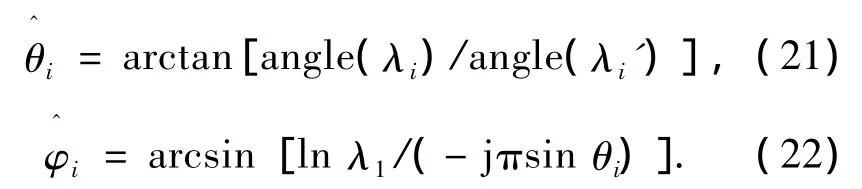
在MUSIC和ESPRIT算法中，对协方差矩阵进行特征分解的时间复杂度近似为O(M3)阶，而估计传播算子的时间复杂度为O(DM2)阶［4］.可见，传播算子算法与MUSIC和ESPRIT算法相比，有着计算量小的优势.本文所提出的改进算法，在PM(propagator method)算法的基础上仅增加了取共轭和子矩阵换位相加的运算，用很少的计算量换取了较高的估计性能.

3 仿真实验

为验证方法的正确性及有效性，采用如图1所示的阵列结构进行了计算机模拟仿真实验，各子阵阵元数M=4，信号的中心频率f=50 MHz，阵元间距d为1/2个信号波长.

实验1:本例给出了方位角和俯仰角在0°～90°范围内变化的估计性能.实验中使俯仰角以5°为间隔，从0°变化到90°，对应每个俯仰角，方位角亦以5°为间隔在0°～90°变化，快拍数200，信噪比5dB，对应每个入射角度做300次独立的仿真实验.图2给出了仿真结果，其中均方根误差定义为

图2 方位角和俯仰角在0°～90°之间变化的均方根误差Fig.2 RMSE of estimation with azimuth and elevation angle varying from 0°to 90°

实验2:基于图1所示的双平行线阵，本例对常规传播算子算法和文中提出的修正传播算子算法的估计性能进行了对比.2个等功率的远场窄带信号入射到图1所示天线阵列，信号源相互独立，二维入射角度分别为［35°20°］和［45°70°］.

图3所示为估计的均方根误差随信噪比变化的曲线，快拍数为250，信噪比从0 dB变化到25 dB，对应每个信噪比做1 000次独立的仿真实验.图4所示为均方根误差随快拍数变化的曲线，信噪比固定为5dB，快拍数从100变化到1 000，对应每个快拍数做1 000次独立的仿真实验.

由图3及图4可以看出，在对非相干信源进行DOA估计时，修正的传播算子算法在信噪比较低和快拍数较少的情况下明显优于常规传播算子算法.可见，采用数据共轭重排的修正传播算子算法可以提高非相干信源的DOA估计性能.

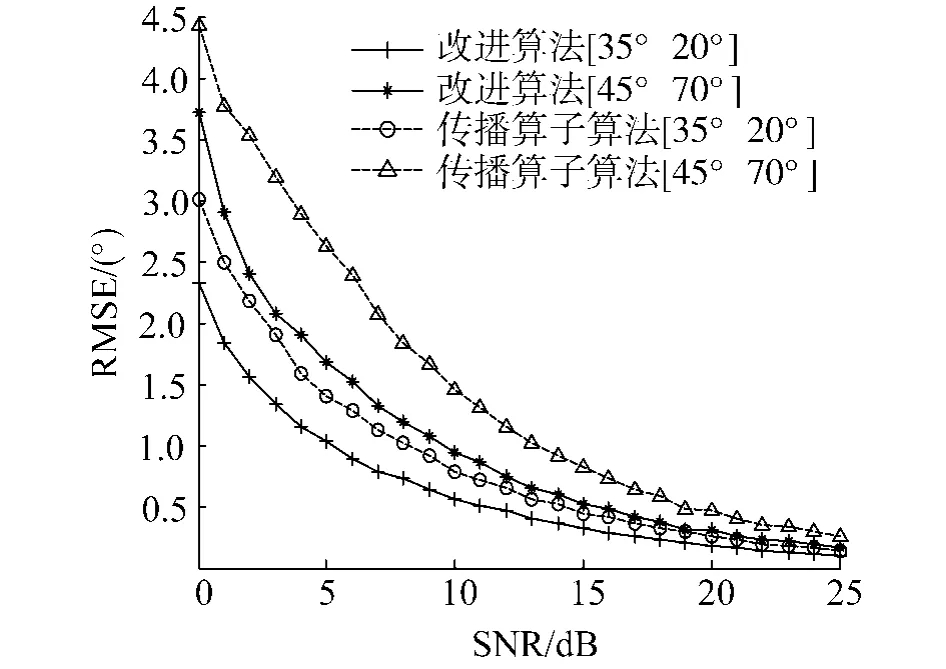
图3 本文算法与常规传播算子算法对比(均方根误差随信噪比变化曲线)Fig.3 Comparison between normal propagator method and thealgorithm proposed in thispaper (RMSE varying with SNR)

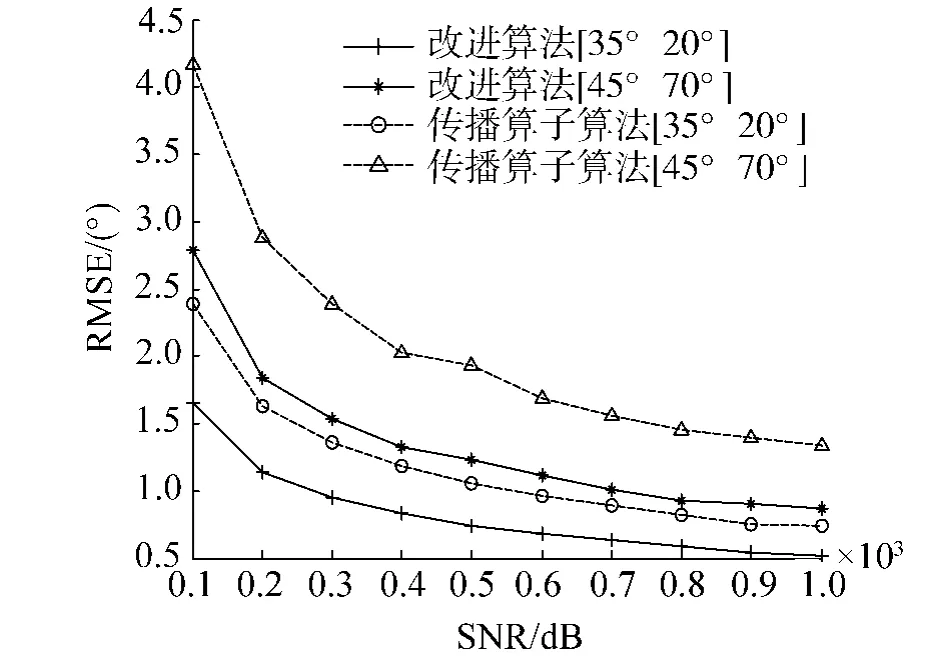
图4 本文算法与常规传播算子算法对比(均方根误差随快拍数变化曲线)Fig.4 Comparison between normal propagator method and thealgorithm proposed in thispaper (RMSE varying with snapshots)

4 结束语

本文在基于双平行线阵的基础上，将数据共轭重排的思想成功的引入到传播算子算法的二维DOA估计中，理论分析和仿真结果表明，改进的算法相当于对协方差矩阵进行了一次前后向平滑，具有平均的意义，可以减少信源间的相关性，提高对非相干信源的估计能力.该方法在低信噪比，小快拍数的条件下仍能获得较好的估计性能，并且有着计算量小的明显优势，具有较好的实用性.

［1］殷勤业，邹理和，NEWCOMB R W.一种高分辨率二维信号参量估计方法:波达方向矩阵法［J］.通信学报，1991，12(4):1-7.

YIN Qinye，ZOU Lihe，NEWCOMB R W.A high resolution approach to 2-D signal parameter estimation:DOA matrix method［J］.Journal of China Institute of Communications，1991，12(4):1-7.

［2］董轶，吴云韬，廖桂生.一种二维到达方向估计的ESPRIT新方法［J］.西安电子科技大学学报，2003，30(5):569-573.

DONG Yi，WU Yuntao，LIAO Guisheng.A novel method for estimating 2-D DOA［J］.Journal of Xidian University，2003，30(5):569-573.

［3］刁鸣，吴小强，张鹏.基于修正ESPRIT算法的二维DOA估计［J］.哈尔滨工程大学学报，2008，29(4):407-410.

DIAO Ming，WU Xiaoqiang，ZHANG Peng.2-D DOA estimation based on a modified ESPRIT algorithm［J］.Journal of Harbin Engineering University，2008，29(4):407-410.

［4］MARCOS S，MARSAL A，BENIDIR M.The propagator method for source bearing estimation［J］.Signal Processing，1995，42(2):121-138.

［5］TAYEM N，KWON H M.L-shape 2-dimensional arrival angle estimation with propagator method［J］.IEEE Transactions on Antennas and Propagation，2005，53(5):1622-1630.

［6］苏淑靖，颜景龙，马维贤，曹东杰.基于传播算子的二维波达方向估计新算法［J］.北京理工大学学报，2008，28 (7):602-605.

SU Shujing，YAN Jinglong，MA Weixian，CAO Dongjie.A new algorithm for 2-D DOA estimation based on propagator method［J］.Transactions of Beijing Institute of Technology，2008，28(7):602-605.

［7］张光斌，廖桂生，吴云韬，王万林.基于数据共轭重排修正的传播算子DOA估计算法［J］.系统仿真学报，2004，16(8):1662-1664.

ZHANG Guangbin，LIAO Guisheng，WU Yuntao，WANG Wanlin.A modified propagator algorithm for DOA estimation based on conjugate data rearrangement［J］.Journal of System Simulation，2004，16(8):1662-1664.

［8］刁鸣，缪善林.二维ESPRIT算法参数的快速配对［J］.哈尔滨工程大学学报，2008，29(3):290-293.

DIAO Ming，MIAO Shanlin.Fast parameter matching for 2-D ESPRIT algorithm［J］.Journal of Harbin Engineering University，2008，29(3):290-293.