移动传感器对关键点的监测问题研究

朱齐丹，吴叶斌，姚姗姗，陆军

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

无线传感器网络具有广泛的应用范围，其中包括侦查，环境监测，生态系统监测，森林火灾的响应，医疗监护，等等［1-8］.在传统的无线传感器网络模型中，静态传感器节点以极高的密度随机分布在工作空间中，使该传感器网络覆盖整个工作空间并且使传感器网络保持连接.但是，这种方法有几个缺点: 1)由于传感器的位置是固定的，所以没有被覆盖的区域永远无法被监测;2)在监测网络中，如果对手获得传感器的位置信息，它可以利用这些信息避开传感器;3)在传感器密度较低的区域，一旦有传感器发生故障可能导致整个传感器网络无法连接.最后，静态传感器网络无法适应动态环境下可能出现的新的情况，因而妨碍正常的感知和通讯任务.

移动传感器能够解决静态传感器所面临的大多数问题，并且已经成功应用于大型工作空间［5］.由于这种机动性的存在，从而可以用少量的传感器覆盖所有敏感区域.随机运动的策略可以使对手难以确保不被传感器发现.由于可以运动，当他们来到对方的传输范围时，传感器之间可以相互交换数据，也可以给中央节点(接收器)发送信息.这就保持了网络的连接.虽然移动传感器在一段时间内能够覆盖更多的区域，但是可能出现多个机器人同时探测同一区域的情况.因此，没有适当的运动规划，移动传感器网络不能有效完成对整个工作空间的覆盖，使得该传感器网络错过了发现未被覆盖区域的事件，从而使探测效率大大降低.

文献［9-12］研究了静态传感器的覆盖问题.文献［13］和文献［14］研究了动态传感器的运动规划问题，但是没有研究动态传感器的覆盖效率与动态传感器的速度之间的关系.文献［10］是最早的一篇研究无线传感器网络的覆盖问题的论文，用图论的方法研究了无线传感器网络的覆盖问题.文献［15］采用栅格法研究了无线传感器网络完成对工作区域覆盖和保持通讯的充分必要条件.文献［16-18］研究了无线传感器网络的能源效率问题.

针对静态传感器无法覆盖整个工作空间，易被对手利用和无法适应新情况等缺点，提出用移动传感器对事件进行监测，弥补了静态传感器的不足;为了提高监测效率，提出了移动传感器的运动规划方法.

1 移动传感器对关键点的监测问题研究

1.1 问题描述

随机事件在工作空间的某一固定点出现和消失，这一固定点称为关键点.如果移动传感器在事件消失之前发现事件，称随机事件被监测到，如果随机事件在移动传感器到达之前消失，那么称随机事件丢失.在关键点处事件的出现和消失的时间分布是已知的.本文的目的是给出移动传感器的运动规划，用于满足事件监测的指标.在本文中，假设关键点的集合是有限离散集.

本文提出的方法应用范围极为广泛，如监视、检测、水下网络传感器和供应链管理.

本文假设以下3点:

1)每个关键点只被一个移动传感器监测，如果每个关键点可以被多个传感器监测，会使问题的复杂度大大增加.

2)为了使每个传感器需要与中央控制器能够通信，传感器的路径从中央控制器所在地开始，最后还要回到起点，把收集到的数据发送给中央控制器.

3)移动传感器的速度是相同的.

1.2 关键点事件监测问题的性能分析

本节对移动传感器网络覆盖效率的性能进行了分析.假设有a个关键点，分布在长度为D的闭合曲线C上.传感器沿着C运动，传感器的探测半径为r，相邻关键点之间的距离大于2r，当传感器与关键点的距离小于r时才能对此处的事件进行监测.

关键点的状态在0和1之间变化.状态0代表事件出现，状态0代表事件消失.状态0和状态1的持续时间服从指数分布，它们的均值分别为和本文设λ=μ∀i.

假设传感器以速度v沿着C运动，事件完成一个0→1→0或1→0→1变化称为一个循环.L代表一个状态循环的均值:

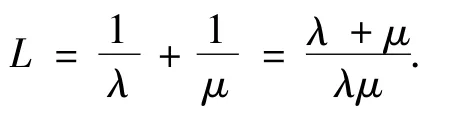
移动传感器沿着C运行一周，经过各关键点一次.每个关键点能被传感器监测的时间为如果在t时刻，传感器发现一个关键点.那么传感器将在这段时间内对该关键点进行监测.传感器监测到的事件的数量取决于关键点在t时刻的状态，和在时间段的循环次数.定理1 用C(τ)表示在时间段(t，t+τ)关键点的状态循环次数，那么在这段时间内状态循环次数的数学期望为

证明:事件的状态循环是一个更新过程，消失和出现的时间是2个服从指数分布的随机变量，在时间τ内更新次数的数学期望的拉普拉斯变换为［19］

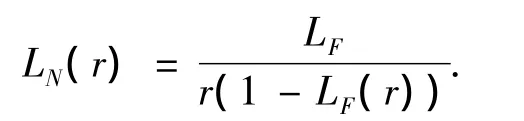
其中，LF(r)是完成一个更新过程所需时间的拉普拉斯变换.

用T表示完成一次更新过程所需要的时间，则T=T1+T2，T1和 T2服从均值为和的指数分布，则T的概率分布为

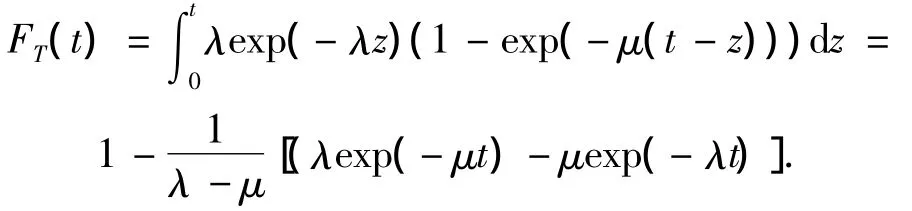
因此，T的概率密度为

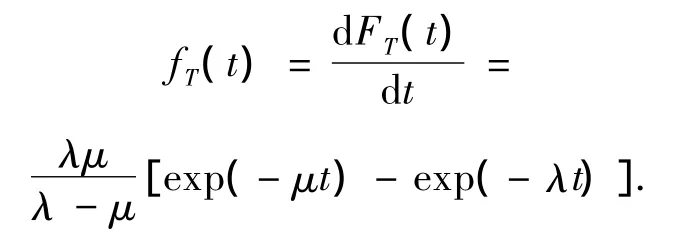
fT(t)的拉普拉斯变换为

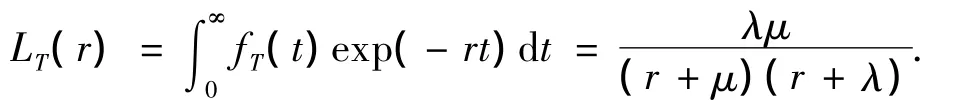
由文献［3］得E［C(τ)］的拉普拉斯变换为

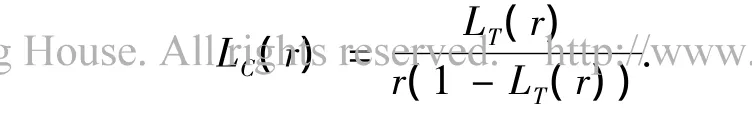
那么，

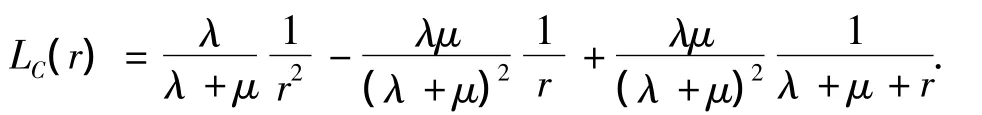
因此在时间τ内的更新次数的数学期望为

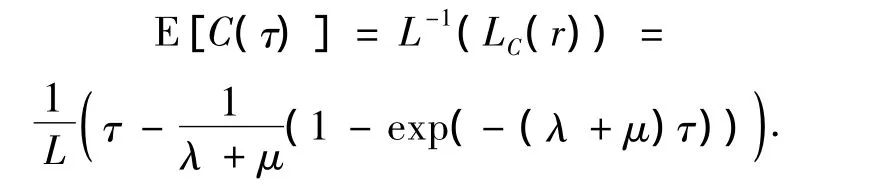
证毕.

用Si(t)表示在t时刻的状态，P0和P1分别表示在t时刻Si(t)=0和Si(t)=1的概率，因此

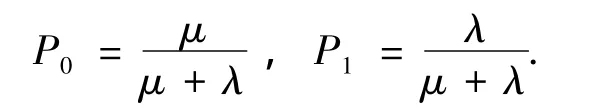
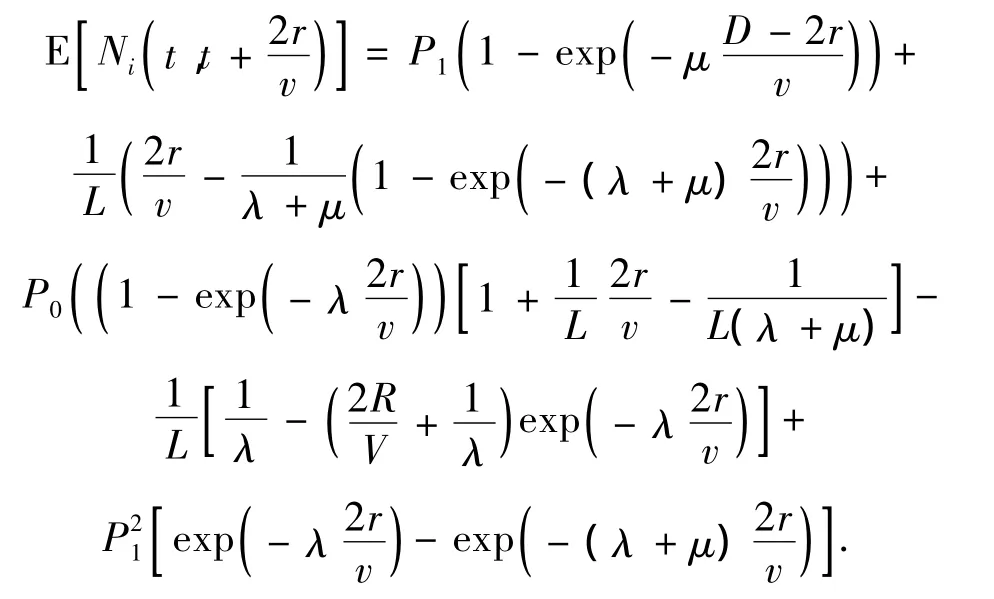
证明:当t时刻Si(t)=1时，移动传感器监测到的随机事件的数量为表示移动传感器经过一个关键点2次捕获到同一事件的概率，则当Si(t)=1时，移动传感器监测到的随机事件数量的数学期望为

当t时刻Si(t)=0时，t'表示关键点的状态由0变为1所需要的时间，当t时刻Si(t)=0时，移动传感器监测到的随机事件数量的数学期望为

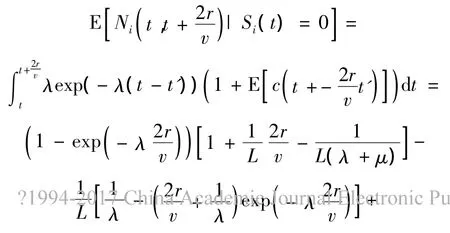
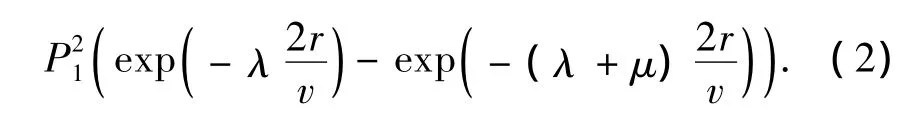
合并(1)、(2)得证.

证毕.

定理3 移动传感器监测到的事件的比例为

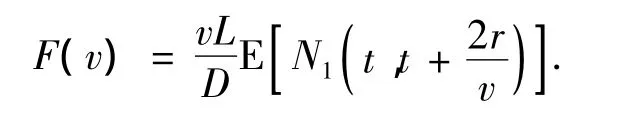
证明:移动传感器沿着C运行一圈，捕获到的事件的数学期望记为Nr，Nr的数学期望是移动传感器在每个关键点处捕获的事件的数学期望之和，即

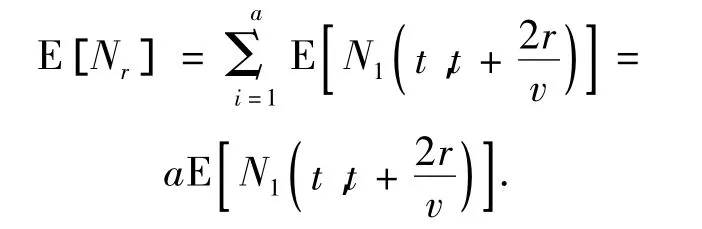
NT'表示在时间［0，T］随机事件出现的总数:

当T→∞时，移动传感器捕获到的事件的比例为

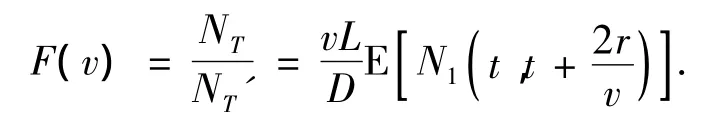
证毕.

1.3 移动传感器的运动规划

假设有k个移动传感器，本节提出一种运动规划方法，使得每个关键点只被一个移动传感器监测，并且至少被一个移动传感器监测，同时使监测效率尽可能大.每个移动传感器都是从中央控制器所在位置出发，最后回到出发点.这是旅行商问题的一种变形，属于k-TSP问题为:k个人从城市1出发分头去访问n－1个城市，每个城市有且仅有一个人到达，最后都回到城市1.问怎样安排使得k个人的总访问路线最短.k-TSP是TSP的一种变形，同样是NP困难的，因此从理论的角度看，是不可能设计出理想的(多项式时间)能求出最优解的精确算法.本节通过一种启发式的方法同时建立k条路径.

令Ri=(vi1，…，vim)为其中的一条子路径，其中vi1=vim.存在一节点u∉Ri，则把u插入到vi和vi+1之间的代价函数为

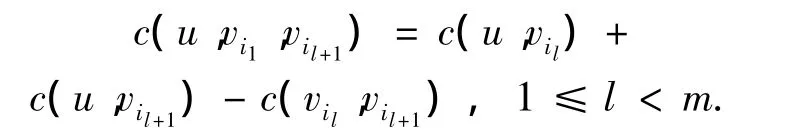
u插入到子路径Ri中时，总是把u插入到Ri中的相邻节点之间，并且使得路径的总代价最小，记为Ri←(u).总路径R的代价函数为:c(R)=Fk(v)，Fk(v)为在总路径R上移动传感器捕获到的事件的效率:

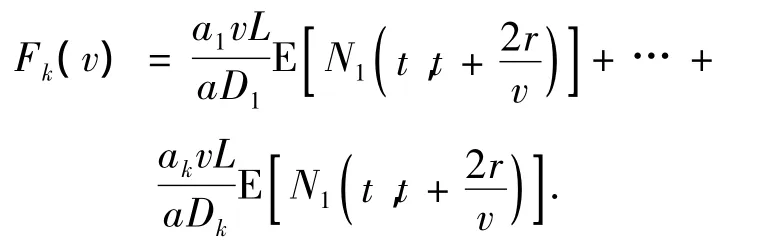
算法如下:

1)初始化k个路径，Rj=(v0，v0)∀1≤j≤k.其中v0代表中央控制器的位置，工作空间中的关键点所在位置分别用序号(v1，…，vm)表示.

2)对于每一个不在(R1，R2，R3，…，Rk)中的关键点vj，1≤j≤a，计算出vj插入到Ri中的代价函数Fk(v)，存在一个vj和Ri，使得当vj被加进Ri时，Fk(v)增加最大.

3)如果由2)得到的结果是Ri和vj，则把vj插入到Ri中，即Ri←(vj).

4)如果(R1，R2，R3，…，Rk)中包含了所有的关键点，则算法终止，否则转到2).

2 仿真实验与分析

根据以上对移动传感器的分析和设计，在Visual C++和Matlab下进行仿真实验，比较了移动传感器与固定传感器的监测效率，分析了移动传感器的数量和速度对捕获效率的影响.如果有m个固定传感器分布在工作空间中，a个关键点分布在工作空间中，并且m≤a每个传感器监测一个关键点，则监测效率为m/a.如果相同数量的移动传感器的捕获效率Fm(v)＞m/a，则使用移动传感器更加有效.本节在500 m×500 m的环境中进行仿真，取参数r=10 m，a=9，λ=μ=0.01，k分别取1、2、3.如图1～3所示.图中的黑点代表中央控制器的位置，圈的圆心代表关键点，圆代表随机事件能被感知的范围.图1～3分别为有1个、2个、3个传感器的运动规划情况.

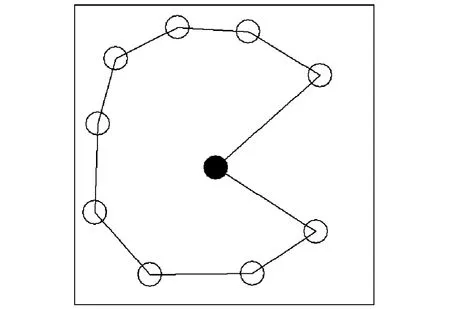
图1 1个移动传感器的运动规划Fig.1 The motion planning of one mobile sensor

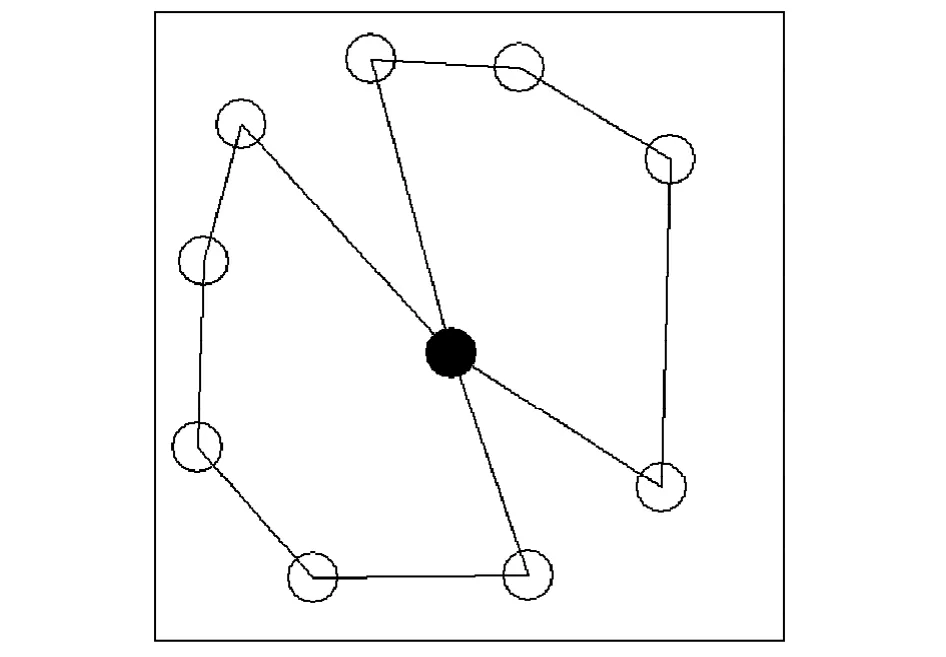
图2 2个移动传感器的运动规划Fig.2 The motion planning of two mobile sensors

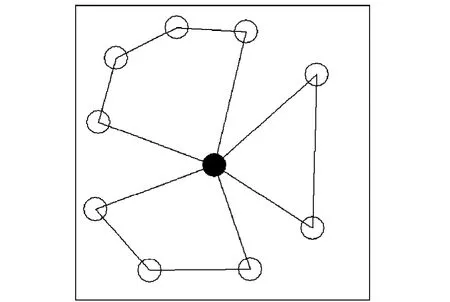
图3 3个移动传感器的运动规划Fig.3 The motion planning of three mobile sensors

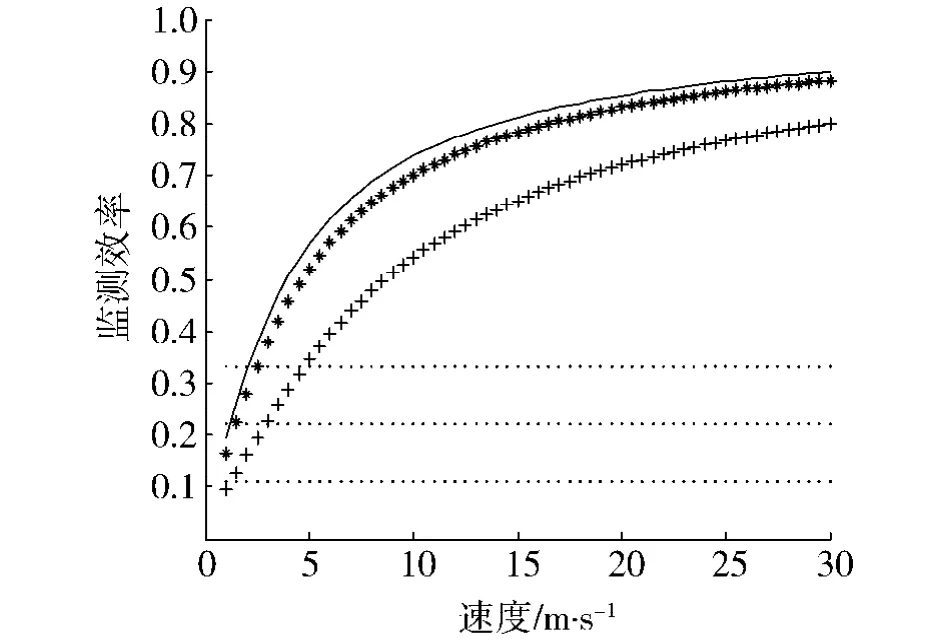
图4 移动传感器时监测到的随机事件与移动传感器速度的关系Fig.4 The relationship between Stochastic event capture and the speed of mobile sensors

图4中的“+”线代表只有一个移动传感器时监测到的随机事件与移动传感器的速度的关系，“*”线代表有两个移动传感器时监测到的随机事件与移动传感器的速度的关系，实线代表有3个移动传感器时监测到的随机事件与移动传感器的速度的关系，其他虚线代表固定传感器的监测效率.从图形可以看出，随着速度的增加，移动传感器监测到的随机事件的效率也在增加;当速度超过某一值时，移动传感器的监测效率就会大于固定传感器的监测效率，随着移动传感器数量的增加捕获效率随之增加.

3 结束语

本文对移动传感器的捕获效率进行了分析，并且提出了一种移动传感器的运动规划方法.通过仿真实验验证了路径规划方法的可行性，并且分析了监测效率与移动传感器的数量和速度的关系，也比较了移动传感器和固定传感器监测性能.结果表明随着速度的增加移动传感器监测到的随机事件的效率也在增加，当速度超过某一值时，移动传感器的监测效率就会大于固定传感器的监测效率，随着移动传感器数量的增加捕获效率随之增加，但是增速越来越缓慢.

［1］KAHN J M，KATZ R H，PISTER K S.Next century challenges:mobile networking for smart dust［C］//Proceedings of 5th Annual ACM/IEEE International Conference on Mobile Computing and Networking.New York，USA，1999: 271-278.

［2］POTTIE G J，KAISER W J.Wireless integrated network sensors［J］.Communications of the ACM，2000，43(5): 51-58.

［3］LEONCINI M，RESTA G，SANTI P.Analysis of a wireless sensor dropping problem in wide-area environmental monitoring［C］//Proceedings of 4th International Symposium on Information Processing in Sensor Networks.Los Angeles，USA，2005:239-245.

［4］STEERE D C，BAPTISTA A，MCNAMEE D.Research challenges in environmental observation and forecasting systems［C］//Proceedings of 6th Annual ACM/IEEE International Conference on Mobile Computing and Networking.New York，USA，2000:292-299.

［5］MAINWARING A，CULLER D，POLASTRE J.Wireless sensor networks for habitat monitoring［C］//Proceedings of 1st ACM International Conference on Wireless Sensor Networks and Applications.New York，USA，2002:88-97.

［6］MEGUERDICHIAN S，KOUSHANFAR F，QU G.Exposure in wireless ad-hoc sensor networks［C］//Proceedings of 7th Annual ACM/IEEE International Conference on Mobile Computing and Networking.New York，USA，2001:139-150.

［7］CHEN M X，WANG Y D.An efficient location tracking structure for wireless sensor networks［J］.Computer Communications，2009，32(13):1495-1504.

［8］YANG H，SIKDAR B.A protocol for tracking mobile targets using sensor network［C］//Proceedings of IEEE International Workshop on Sensor Network Protocols and Applications，2003:71-81.

［9］HUANG C F，TSENG Y C.The coverage problem in a wireless sensor network［C］//Proceedings of 2nd ACM International Conference on Wireless Sensor Networks and Applications.New York，USA，2003:115-121.

［10］MEGUERDICHIAN S，KOUSHANFAR F，SRIVASTAVA P M.Coverage problems in wireless ad-hoc sensor networks［C］//Proceedings of 20th Annual IEEE Conference on Computer Communications.New York，USA，2001: 1380-1387.

［11］WANG X，XING G，ZHANG Y.Integrated coverage and connectivity configuration in wirelesssensornetworks［C］//Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems.New York，USA，2003:28-39.

［12］XING G，LU C，PLESS R.Cogrid:an efficient coverage maintenance protocol for distributed sensor networks［C］// Proceedings of 3th International Symposium on Information Processing in Sensor Networks.New York，USA，2004: 414-423.

［13］LATOMBE J C.Robot motion planning［M］.Norwell: Kluwer Academic Publishers，1991:95-97.

［14］LAVALLE S M.Planning algorithms［M］.Cambridge: Cambridge University Press，2006.

［15］SHAKKOTTAI S，SRIKANT R，SHROFF N B.Unreliable sensor grids:Coverage，connectivity and diameter［J］.Ad Hoc Networks，2006，3(6):702-716.

［16］HSIN C F，LIU M.Network coverage using low duty-cycled sensors:random ＆ coordinated sleep algorithms［C］//Proceedings of 4th International Symposium on Information Processing in Sensor Networks.New York，USA，2004:433-442.

［17］KUMAR S，LAI T H，BALOGH J.On k-coverage in a mostly sleeping sensor network［C］//Proceedings of 10th Annual ACM/IEEE International Conference on Mobile Computing and Networking.New York，USA，2004:144-158.

［18］TIAN D，GEORGANAS N D.A coverage-preserving node scheduling scheme for large wireless sensor networks［C］// Proceedings of 2nd ACM International Conference on Wireless Sensor Networks and Applications.New York，USA，2002:32-41.

［19］GALLAGER R G.Discrete stochastic processes［M］.Norwell:Kluwer Academic Publishers，1995:251-254.