基于拟单边Lipschitz条件的一类非线性系统降维观测器设计

徐明跃，胡广大

(1.哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001;2.北京科技大学 信息工程学院，北京 100083)

线性及非线性系统的观测器设计问题十分重要，它是控制理论的核心问题，得到了广泛应用.诸如:输出反馈控制、过程辨识、系统控制、故障诊断等.对于线性系统状态观测器的设计方法，在文献［1-2］中就已经得到了完美解决.比起线性系统，非线性系统观测器设计要复杂和困难得多，至今仍有许多尚待解决的问题.近几十年来，非线性状态观测器设计一直是众多学者研究的热点，得到了很多设计方法.如非线性坐标变换、自适应观测器、高增益技术、标准型和输出嵌入、光滑和非光滑技术等［3-8］.这些方法或是给出的条件比较严格以确保系统能够转化为便于观测器设计的形式，或是针对特殊结构的非线性项，或是增加假设条件已得到具有局部收敛的观测器.所以，为了得到尽可能较少保守性的更一般的设计方法，非线性系统观测器设计问题至今仍是许多学者研究的热点.非线性系统的状态观测器可分为全维观测器和降维观测器两种.降维观测器只估计系统的部分状态变量，这些变量不能从输出中直接测量.由于降维观测器的维数比全维观测器的维数低，因此，构造观测器时可以用较少的积分仪并且整个控制系统更简单.

在实际问题中遇到的系统大多都为 Lipschitz非线性系统，许多非线性系统的非线性项或是Lipschitz的或是局部Lipschitz的.近年来，许多学者致力于Lipschitz非线性系统状态观测器的研究，得到了大量设计方法［9-14］.但基于Lipschitz条件得到的渐近稳定观测器存在的充分条件，具有强的保守性，原因在于Lipschitz常数是个正数.文献［15-17］中引入比Lipschitz条件更弱的拟单边Lipschitz条件来代替Lipschitz条件，研究了Lipschitz非线性系统全维观测器的设计方法，设计方法比已有方法减少了保守性.

沿文献［15-20］的思路，基于拟单边、弱拟单边Lipschitz条件，给出Lipschitz非线性系统的降维观测器设计方法，得到比现有的设计判据减小保守性的渐近稳定观测器存在的判据.不同于现有文献的方法，使所得到的设计方法在系统的参数不满足可检测性时仍然可用.最后通过仿真算例，验证了所得到方法的正确性.

1 模型描述

假定I代表适当维数的单位阵，Eij表示第i行第j列元素是1其余元素是0的适当维数方阵.

考虑如下的Lipschitz非线性系统:

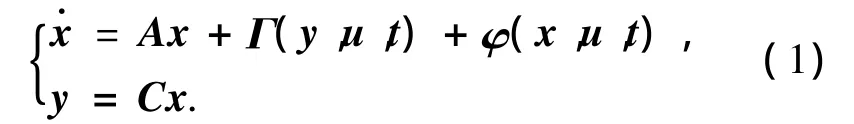
其中，x∈Rn为状态向量，u∈Rm为输入，y∈Rp为输出，A∈Rn×n，C∈Rp×n为常值矩阵.Γ(y，u，t)是n维已知向量函数，φ(x，u，t)是n维已知向量函数并且关于x是非线性的.

在文献［15-17］中引入了拟单边Lipschitz条件:

来代替通常的Lipschitz条件.其中f(x，u，u)= Pφ(x，u，t)，P是待求正定阵，M是一个实对称阵(不必正定或负定)，称M为Pφ的拟单边Lipschitz常数矩阵.称函数φ(x，u，t)满足条件拟单边Lipschitz条件.

在设计非线性系统观测器时，用拟单边Lipschitz条件(2)代替通常的Lipschitz条件的优越性在文献［15-17］中已经讨论.此外，易见，满足通常Lipschitz条件的函数一定满足拟单边 Lipschitz条件(2).

在很多情况下，可以找到不定的甚至负定的拟单边Lipschitz常数矩阵M，这就使得拟单边Lipschitz常数矩阵M(尤其是负的M)比通常的Lipschitz常数能更多反映非线性部分对观测器稳定性的贡献.

将矩阵A和对称正定阵P分块如下:

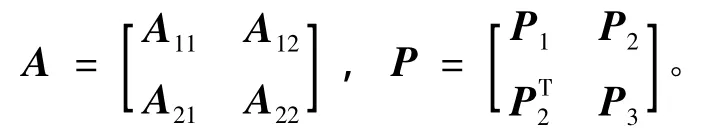
式中:A11、p1∈Rp×p、A12，p2∈RP×(n－P)，A21∈

2 降维观测器设计

基于拟单边Lipschitz条件(2)，可以得到下列重要结果.

定理1 假定C=［Ip0］，并且系统(1)满足拟单边Lipschitz条件(2).如果

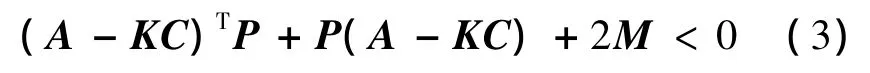
有正定解P，其中M为Pφ的拟单边Lipschitz常数矩阵.那么非线性系统(1)存在n－p维的降维观测器:

式中:

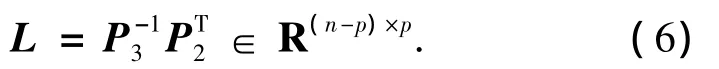
用式(7)减去式(4)的第1个式子，则动态误差满足:

式中:

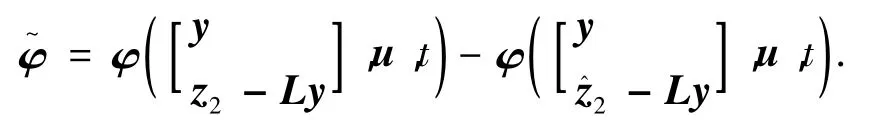
考虑Lyapunov函数

其导数为

因为x=T－1z，拟单边Lipschitz条件(2)意味着

即

结合式(5)、(8)和(9)得

这就意味着式(4)是式(1)的渐近稳定降维观测器.

定义1 考虑非线性向量函数φ(x，u，t).如果

成立.其中P是某待求正定阵，M是一个实对称阵(不必正定或负定)，则称φ(x，u，t)满足弱拟单边Lipschitz条件.

从定理1的证明过程可见，在C=［Ip0］的情况下，定理1的条件“系统(1)满足拟单边Lipschitz条件(2)”可以减弱为“系统(1)满足弱拟单边Lipschitz条件(10)”.

定理2 如果非线性系统(1)满足弱拟单边Lipschitz条件(10)，C=［Ip0］，并且存在增益阵K使得

有正定解P，则系统(1)有形如式(4)的降维观测器.

类似于文献［20］的讨论，如果C≠［Ip0］，但C有行满秩，则可以得到类似定理1的结论.即利用Gram-Schmidt正交化，存在可逆阵S∈Rp×p使得C=，其中∈Rp×n且=Ip.运用输出变换ω=S－1y=，将矩阵扩充为 n×n的正交阵通过状态变换，式(1)变为

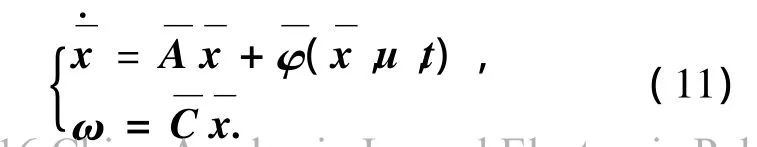
引理1 考虑非线性系统(1).如果条件(2)成立，并且可以选择K满足式(3)，则可以选择WKS使得

引理1的证明完全类似于文献［20］中引理1的证明(略).

定理3 假设C行满秩，且非线性系统(1)满足拟单边Lipschitz条件(2).如果存在增益阵K使得(A－KC)TP+P(A－KC)+2M＜0有正定解P，则系统(1)有具有如下形式的降维观测器:

事实上，注意到W是n×n的正交阵，有

由式(11)、(14)、引理1和定理1可知式(13)是系统(1)的渐近稳定降维观测器.

定理3得证.

3 观测器渐近稳定性的仿真试验

下面就(A，C)可检测与不可检测2种情况下通过仿真实例验证提出的降维观测器设计方法的有效性以及所得判据比基于Lipschitz条件得到的判据减小保守性.

试验1 考虑非线性系统(1)，其中

由Matlab的LMI工具箱解(17)得

图1给出了状态变量x2的仿真结果，从图1可以看出所设计的非线性降维观测器实现了对例1所给系统的状态变量x2的渐近估计，其中初值x(0)=1，(0)=0.6.

在例1中容易求得φ(x，u，t)的Lipschitz常数，此时文献［20］中所给方法失效.而由于设计了半负定的拟单边Lipschitz常数矩阵M，从而把非线性项对于观测器渐近稳定的贡献充分地挖掘了出来.由此可见基于拟单边Lipschitz条件比基于Lipschitz条件得到的观测器设计判据大大地减小了保守性.

图1 试验1的状态x2的仿真Fig.1 The simulations for state x2of experiment 1

下面的例子验证了所给的方法即使在系统的参数(A，C)不可检测时，仍然可用.

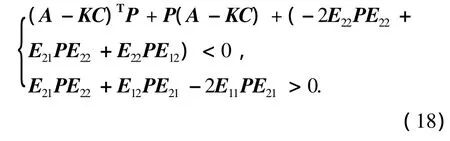
由Matlab LMI工具箱解式(18)得

图2给出了状态变量x2的仿真结果，从图2可以看出所设计的非线性降维观测器在(A，C)不可检测情况下实现了对例2所给系统的状态变量x2的渐近估计，其中初值

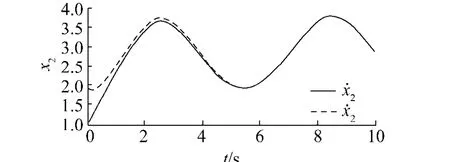
图2 试验2的状态x2的仿真Fig.2 The simulations for state x2of experiment 2

4 结束语

通过设计不定、半负定或负定的拟单边Lipschitz常数矩阵得到了一类非线性系统降维观测器设计的判据，用拟单边Lipschitz、弱拟单边Lipschitz条件来代替通常的Lipschitz条件，给出了了该类非线性系统降维观测器渐近收敛的LMI形式的充分条件.该充分条件比现有文献利用Lipschitz条件给出的充分条件大大减少了保守性.同时解决了非线性系统的参数(A，C)不可检测时现有文献判据失效的问题.所给判据不仅适用于通常的Lipschitz非线性系统，也适用于非Lipschitz非线性系统.仿真算例验证了所给方法的有效性.

［1］KALMAN R E.On a new approach to filtering and prediction problems［J］.Transactions of the ASME Journal of Basic Engineering，1960，82(D):35-45.

［2］LUENBERGER D.An introduction to observers［J］.IEEE Transactions on Automatic Control，1971，16(6):596-602.

［3］DEZA F，BOSSANNE D，BUSVELLE E.Exponential observer for nonlinear systems［J］.IEEE Trans on Autom Control，1993，38(3):482-484.

［4］CICCARELLA C，DALLAMORA M，GERMANI A.A Luenberger-like observer for nonlinear systems［J］.Int J Control，1993，57(3):537-556.

［5］NIKOUKHAH R.A new methodology for observer design and implementation［J］.IEEE Trans on Autom Control，1998，43(2):229-234.

［6］WANG H，HUANG Z J，DELEY S.On the use of adaptive updating rules for actuator and sensor fault diagnosis［J］.Automatica，1997，33(2):217-225.

［7］KREISSELMEIER G，ENGEL R.Nonlinear observers for autonomous Lipschitz continuous systems［J］.IEEE Trans Autom Control，2003，48(3):397-401.

［8］XIA X，ZEITZ M.On nonlinear continuous observers［J］.Int J Control，1997，66(6):943-954.

［9］THAU F E.Observering the state of nonlinear dynamic systems［J］.Int J Control，1973，17，471-480.

［10］ZAK S H.On the stabilization and observation of nonlinear dynamic systems［J］.IEEE Trans Autom Control，1990， 35:604-607.

［11］RAGHAVAN S.Observers and compensators for nonlinear systems with application to flexible joint robots［M］.Berkeley:California University，1992.

［12］RAGHAVAN S，HEDRICK J K.Observer design for a class of nonlinear systems［J］.Int J Cntrol，1994，59: 515-528.

［13］GARG V，HEDRICK J.Fault detection filters for a class of nonlinear systems［C］//Proceedings of the American Control Conference.Seattle，USA，1996:1647-1651.

［14］PERTEW A M，MARQUEZ H J，ZHAO Q.H∞observer design for Lipschitz nonlinear systems［J］.IEEE Trans on Autom Control，2006，51(7):1211-1216.

［15］HU G D.Observers for one-sided Lipschitz nonlinear systems［J］.IMA J Math Control Inf，2006，23:395-401.

［16］HU G D.A note on observer for one-sided Lipschitz nonlinear systems［J］.IMA J Math Control inf，2008，25: 297-303.

［17］XU M Y，HU G D，ZHAO Y B.Reduced-order observer design for one-sided Lipschitz nonlinear systems［J］.IMA J Math Control Inf，2009，26:299-317.

［18］RAJAMANI R.Observer for Lipschitz nonlinear systems［J］.IEEE Trans Autom Control，1998，43:397-401.

［19］RAJAMANI R，CHAO Y M.Existence and design of observers for nonlinear systems:relation to distance to unobservability［J］.Int J Control，1998，69:17-731.

［20］ZHU F，HAN Z.A note on observers for Lipschitz nonlinear systems［J］.IEEE Trans Autom Control，2002，47: 1751-1754.