基于ISVM的船舶横摇运动实时预报方法

刘胜，杨震

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

船舶横摇运动时序是一个复杂的动态过程，一般呈现非线性、随机性、非平稳性等特征，目前国内外对船舶横摇时序建模预报展开了很多研究［1-2］，其中有些对线性系统效果较好，不适于非线性系统;有些需要大量样本数据，泛化能力差.而且它们解决的是极短期预报问题，对更长时间的预报精度低，实时性差.另外，实际的横摇时序在数据的收集、传输或处理过程中经常受到一些随机误差的影响而退化，产生各种噪音，噪音可能依赖于横摇时序，也可能与其无关，它们有的服从正态分布，有的幅值较大，还有的是奇异点.理论上，前述模型的建立都没有考虑对依附于时序中的噪音如何进行降噪.支持向量机(support vector machine，SVM)是由Vapnik等人提出的一种全新的小样本机器学习方法［3］，具有很好的泛化能力，得到的是全局最优解，能够解决小样本、非线性、高维数等实际问题，目前已成为机器学习领域的研究热点［4-5］.上海交通大学近年来将SVM应用于船舶运动建模和控制方面，亦取得了一些开创性的成果［6-7］.江娜［8］建立了基于标准SVM的船舶航向控制系统故障组合预报模型，仿真结果表明该模型达到了实时性的要求，但因标准SVM的ε-不敏感损失函数的缺陷，不能够有效处理一些正态分布、幅值较大和奇异点的噪音，所以它从理论上不太适合实际中含有噪音的船舶横摇时序问题.基于以上思想启发，提出一种采用小波核函数和鲁棒损失函数、且具有单松弛变量ξ的新的支持向量机，即改进支持向量机(improved support vector machine，ISVM)，给出了最优问题及回归算法，同时证明所给算法同标准回归算法的最优解在一定条件下是等价的.最后结合船舶横摇运动预报需具有实时性的特点，设计了基于ISVM的船舶横摇运动实时预报模型.

1 鲁棒损失函数

标准支持向量机是实现结构风险最小化(即经验风险与置信风险的和最小)的一种途径，但不是唯一途径.经验风险由损失函数确定［3］，选择不同的损失函数会构造不同的经验风险，从而形成不同形式的支持向量机.在回归估计中，样本集的最优损失函数与样本集数据的内在特性之间存在某种对应关系，ε-不敏感损失函数是一种线性惩罚函数，对于误差小于ε的样本点不予惩罚，Huber损失函数［9］侧重于对正态分布噪音、幅值较大噪音和奇异点的样本进行降噪.考虑样本数据的特征，并综合ε-不敏感损失函数和Huber损失函数各自的优点，设计具有分段式的混合损失函数，即鲁棒损失函数来增加支持向量机的鲁棒性和泛化能力:

式中:ε+μ=εμ，ε≥0，μ≥0.鲁棒损失函数如图1所示.

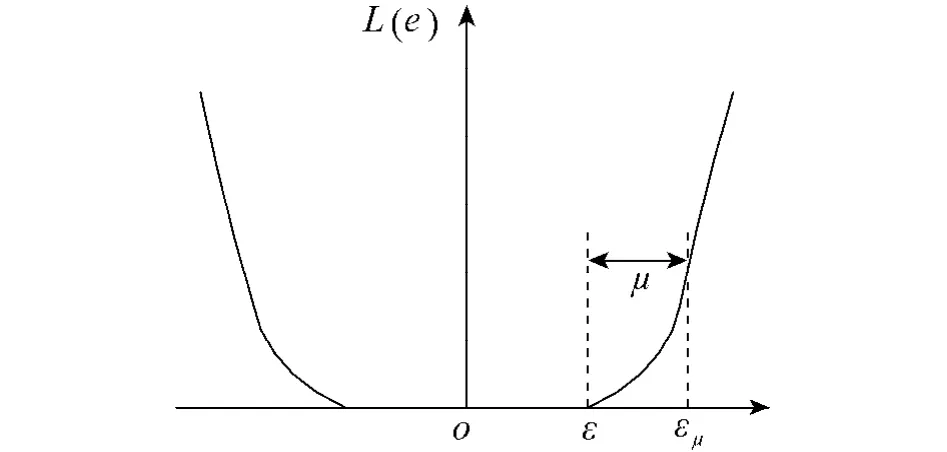
图1 鲁棒损失函数Fig.1 Robust loss function

此损失函数将松弛变量的作用区间分为3个:

1)|e|≤ε部分是靠近最优分界的区间，即ε不灵敏区，不惩罚小于ε的偏差，使学习机的解具有稀疏性.

2)ε≤|e|≤εμ部分是二次方区，主要用来抑制符合高斯分布的量测噪音.

3)|e|≥εμ部分是线性区，主要用来抑制幅值较大的噪音和异常点.

在不同的区间段内，损失函数具有不同的形式，这样，落在各个区间内的噪音会被各个区间的损失函数有效压制.

2 小波核函数

选择适当的核函数是支持向量机解决实际问题时的一个关键因素，应用最广泛的是高斯核函数，但高斯核通过平移不能生成L2空间上的一组基，从而导致支持向量机不能逼近L2空间上任意的非线性函数［10］.小波的伸缩和平移可构成L2空间的一组基，而且选择适当的尺度参数可使小波具有低通或带通滤波的功能，因此采用小波核的支持向量机表现出良好的函数逼近能力和一定的抗噪能力.可生成小波框架的母小波都可以用来构造小波核函数，由此，选择Marr小波核作为ISVM的核函数.由Mercer条件、点积小波核定理以及平移不变核定理［11］得出Marr小波核函数为

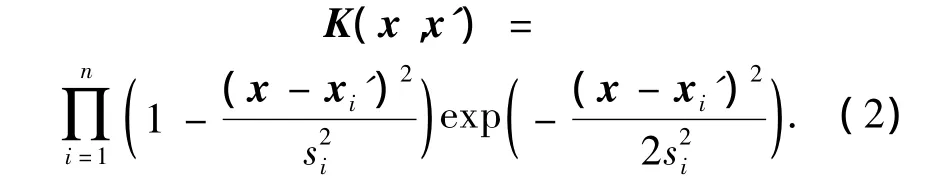
式中:n为样本数据的维数，s为尺度因子.

3 一种改进支持向量回归算法

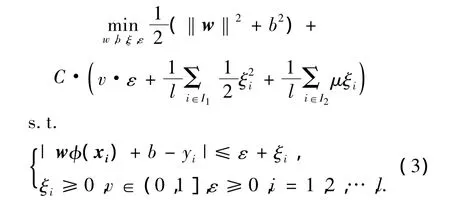
式中:w为高维向量;ξ=［ξ1ξ2… ξl］T;C为惩罚系数，用来控制模型复杂性与训练误差之间的平衡;v为控制支持向量的个数;ε为控制管道大小的参数;ξi(i=1，2，…，l)为松弛变量;I1表示松弛变量落在0＜|ξi|≤εμ区间内的样本集，I2表示松弛变量落在εμ＜|ξi|区间内的样本集.把b2项加入到最优化问题的原问题中可减少一个对偶问题的约束条件，参数b将不会出现在决策函数里，求解过程无需对其进行辨识，提高了计算效率［12］.

为求解上述原问题，引入Lagrange函数:

函数L的极值应满足条件:

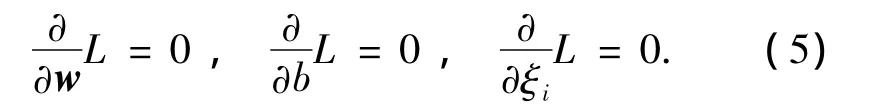
于是得到

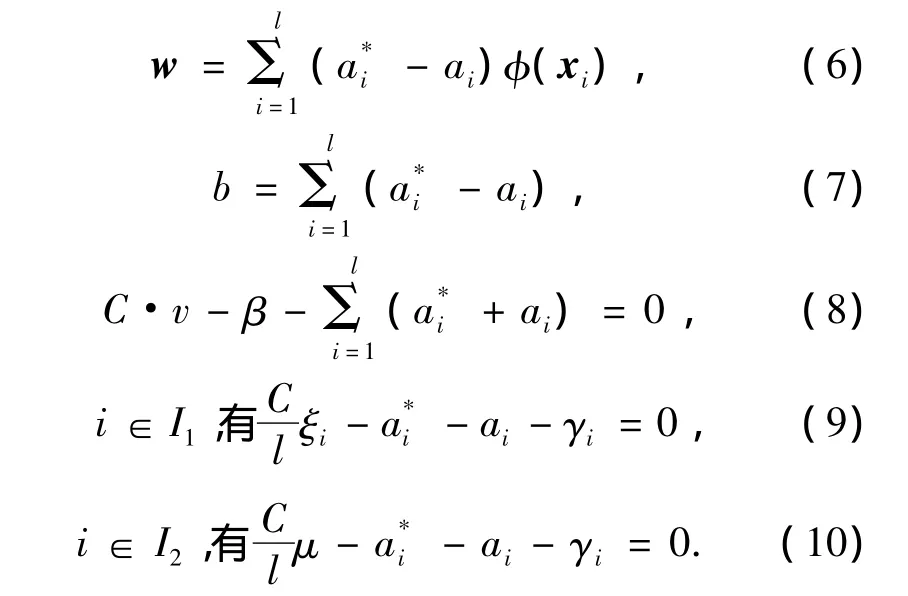
利用Karush-Kuhn-Tuncker(KKT)条件、对偶原理及核函数技术，将式(6)～(10)代入式(3)，得到优化问题的对偶问题如下:

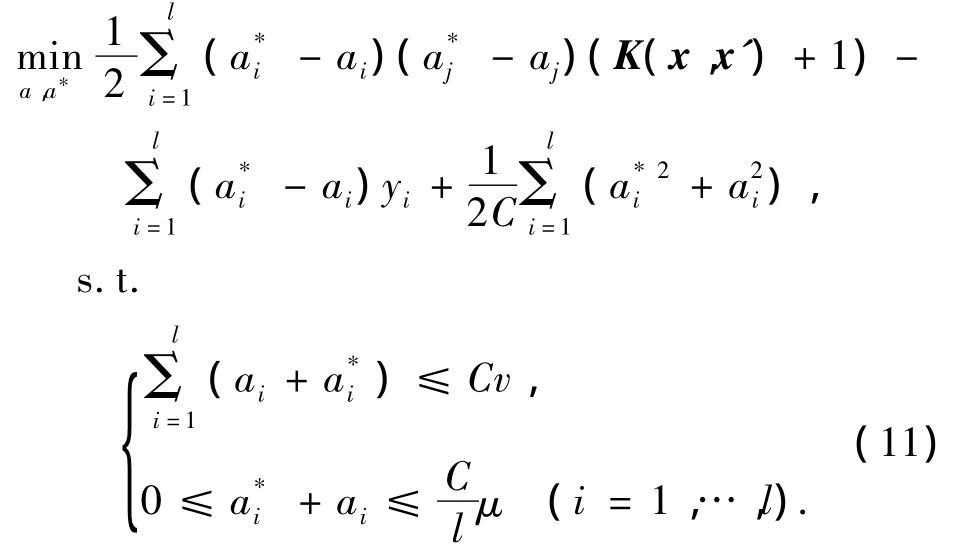
将上式改写成矩阵形式，可得

将式(2)、(6)和(7)代入改进支持向量机的回归估计函数f(x)=w·φ(xi)+b中，得到其输出为

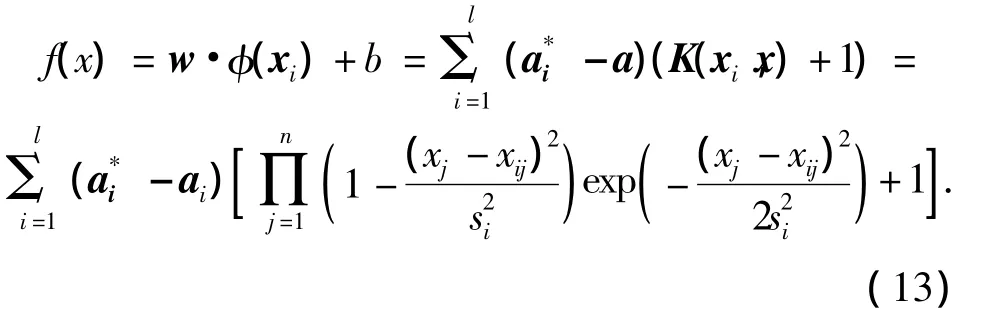
式中:xj表示输入向量x的第j个分量，xij表示第i个训练样本的第j个分量.

4 单松弛变量和双松弛变量(ξ，ξ*)的比较

由以上推导可知，单松弛变量ξ时ISVM的约束条件为式(11)中的约束条件，可以求得双松弛变量(ξ，ξ*)时支持向量机的约束条件为

为了说明方便，将式(11)中单松弛变量ξ时的约束条件记为ST1，将双松弛变量(ξ，ξ*)时的约束条件式(14)记为ST2.下面证明单松弛变量的算法同两个松弛变量时算法的最优解在一定条件下是等价的.

命题 对于式(11)中的对偶问题，约束ST1下的最优解一定是约束ST2下的最优解，反之亦然.

证明 设(a*，a)是约束ST1下对偶问题的最优解，则它必是约束ST2下的可行解.下面用反证法证明它也是约束ST2下的最优解.现假设(a*，a)不是约束ST2下的最优解，则设()为约束ST2下的最优解，于是W()＜W(a*，a)，又由KKT条件可知和不能同时非0，则所以()也是约束ST1下的可行解，于是在约束ST1下有W()＜W(a*，a)，这与(a*，a)是约束ST1下的最优解矛盾，所以(a*，a)也是约束ST2下的最优解.

反之，同理可证.

该命题说明2种约束下对偶问题有相同的最优解.在不影响逼近精度的情况下，单松弛变量ξ的算法使对偶问题更容易求解，而且单松弛变量ξ回归优化中对偶问题的可行域小于双松弛变量(ξ，ξ*)回归优化中的可行域，这样减少了寻优范围，提高了运行速度.

5 基于ISVM的实时预报方法

5.1 预报模型

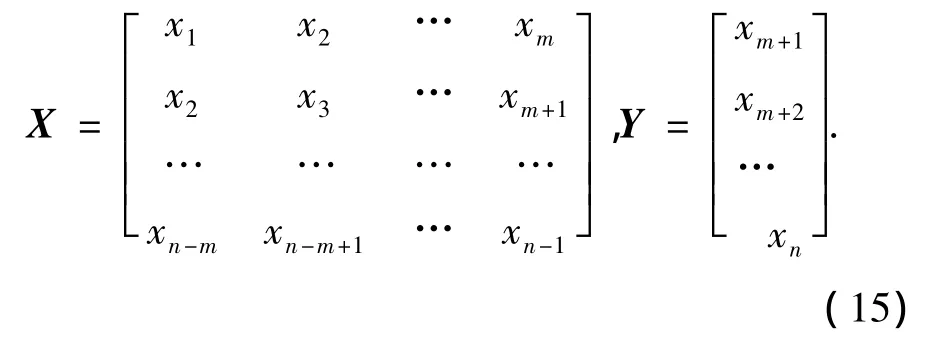
式中:m为嵌入维数，m＜n.m的选取影响预报模型的预报精度，采用最小化支持向量机推广误差的估计来寻找最优的m，考虑估计的无偏性和实用性，选用k-fold交叉验证误差作为推广误差的估计.

对ISVM进行训练的回归函数为

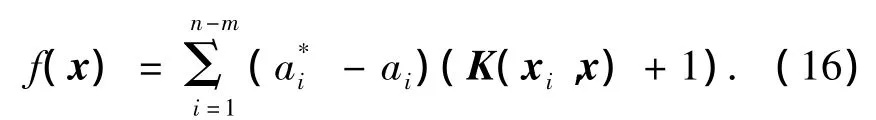
采用离线训练在线实时预报的方式，得到第1步的预报为

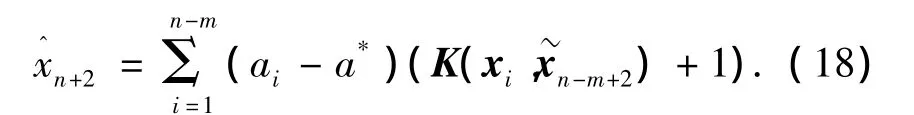
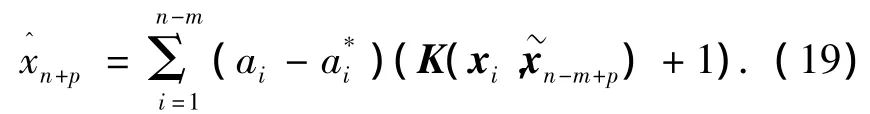
在给定训练样本集下实现实时预报是一个批量处理的过程，随着时间的推移，当第1步到第p－1步的数据可以实际测出后，可以将前p－1步的实际值代替式(19)中的预报值，从而得到第p步的预报值为

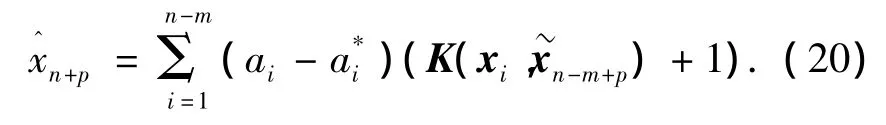
5.2 预报、步骤

ISVM的训练涉及了C、v、μ和核函数中的尺度s这4个参数，本文只考虑μ=1时的情况.则基于ISVM的实时预报步骤如下:

1)对预报时序(xt)进行矩阵变换得到如式(15)的训练样本集，并进行归一化处理;

2)选择式(2)所示的Maar小波核函数K(x， x')，建立形如式(3)的最优化目标函数;

3)将均方误差(mean square error，MSE)作为指标，利用自适应遗传算法［13］对参数(C，v，s)进行寻优，得到最佳参数;

4)求解优化目标函数问题并判断KKT条件，得到支持向量(a*，a);

5)根据实时预报模型式(16)～(19)进行在线实时预报，得到预报值.

6 船舶运动姿态实时预报实例

仿真使用数据为某型号舰船在5级海情有义波高3 m，遭遇浪向角分别为90°和120°时的横摇角度时间序列数据，以及6级海情有义波高4.5 m，遭遇浪向角分别为90°和120°时的横摇角度时间序列数据，共4组数据.用于训练的每组数据的采样周期均为0.5 s，总时长为350 s，即700个采样点数据.根据5.1节中方法得出针对此舰船的最佳嵌入维数为m= 50，则得到形如式(15)所示的训练样本集.运用改进支持向量机算法对训练样本进行训练，并用自适应遗传算法寻优，得到训练模型及参数(C，v，s)的最优组合(48.5，0.72，0.9)，归一化训练样本的MSE为9.48× 10－4，取p=10，依据离线训练结果及实时预报模型对4组样本随后的200个数据点即未来100 s的数据进行实时在线预报，图2～5分别为4种情况下横摇角的真实曲线与预报曲线.预报性能指标用相对均方根误差RMSE(relative mean square error)来表示:

式中:q为总预报步数.

图2 5级海情、浪向角90°时横摇曲线Fig.2 Roll curve of 5 grade sea state and 90°direction of wave

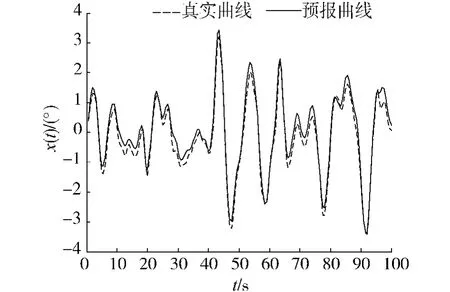
图3 5级海情、浪向角120°时横摇曲线Fig.3 Roll curve of 5 grade sea state and 120°direction of wave

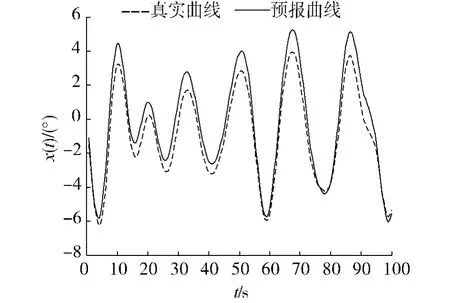
图4 6级海情、浪向角90°时横摇曲线Fig.4 Roll curve of 6 grade sea state and 90°direction of wave

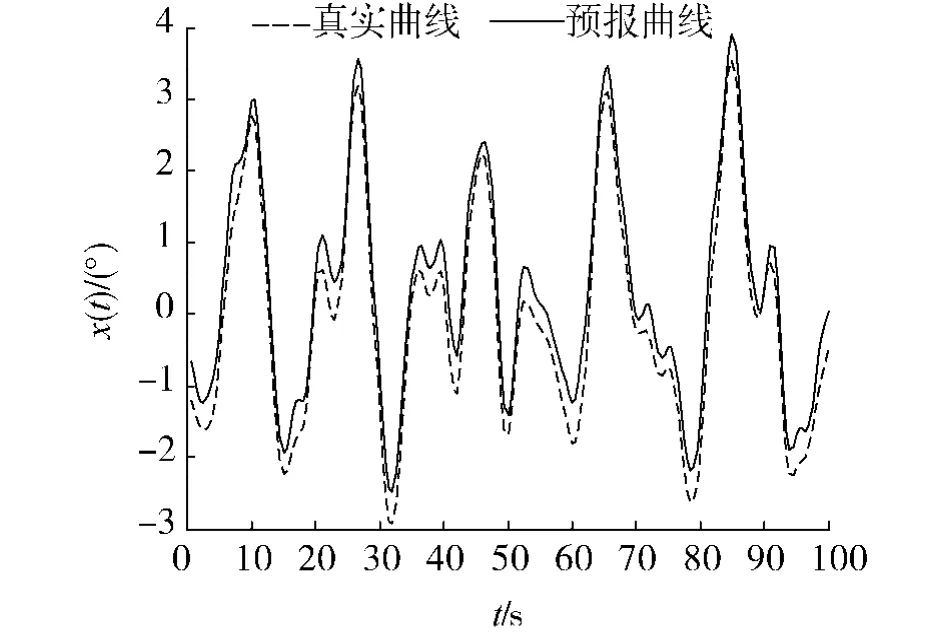
图5 6级海情、浪向角120°时横摇曲线Fig.5 Roll curve of 6 grade sea state and 120°direction of wave

为了更好地说明基于ISVM的实时预报模型在船舶横摇时间序列预报中的优越性，同时也采用了基于ε－支持向量机的神经网络组合预报模型对上述横摇时序进行预报［8］，利用性能指标RMSE对船舶在2种方法下的预报结果进行统计分析，如表2所示.

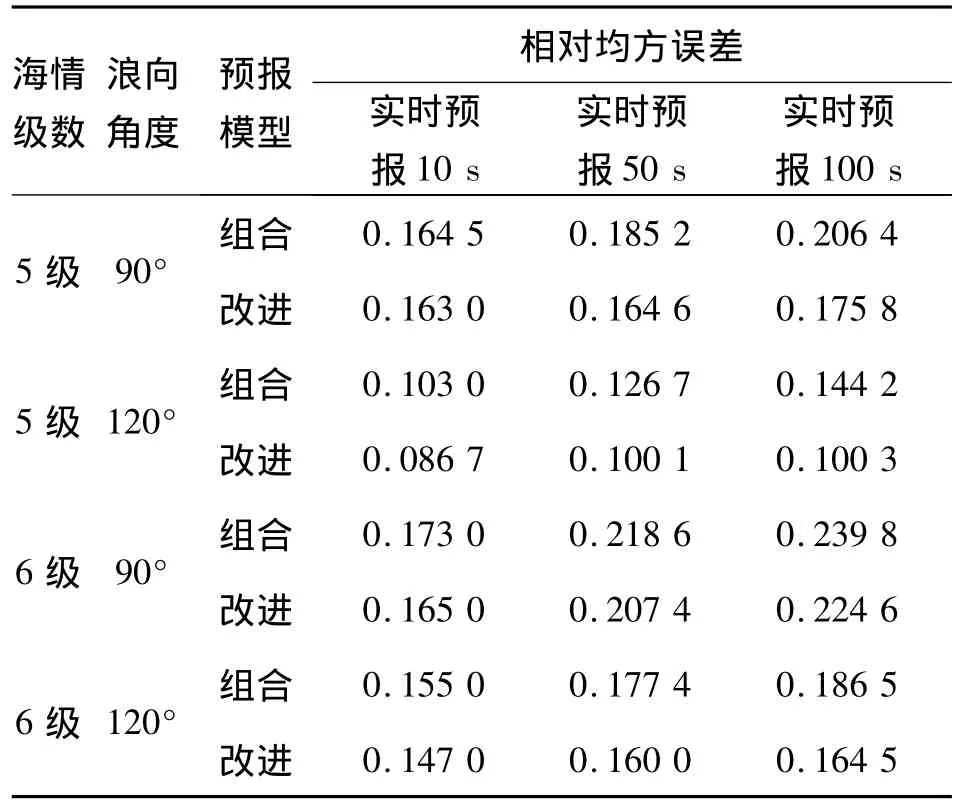
表2 两种实时预报模型的误差统计Table 2 Error statistics of two prediction models

可见，对于仿真所用的船舶横摇时间序列，给出的具有鲁棒损失函数的ISVM实时预报模型的误差指标值RMSE好于基于标准支持向量机组合预报模型RMSE.而求解改进支持向量机的过程实际上与标准支持向量机一样，都是求解一个凸二次规划问题，说明基于改进支持向量机的实时预报方法是行之有效的.

7 结束语

文中提出的采用鲁棒损失函数的ISVM较标准SVM具有更强的鲁棒性，可以有效压制样本数据中的混合噪音，提高回归精度及泛化能力;单松弛变量ξ下的回归算法因寻优范围的减小使得运行速度快于标准算法，因此，单松弛变量回归算法是一种能够保持同样性能的标准算法的简化;从实例仿真结果可以看出，基于ISVM建立的船舶横摇运动实时预报模型具有良好的性能，比基于标准SVM的神经网络组合预报模型的预报精度高，且具有较强的泛化能力，易于在工程实际中应用.同时还可以将其应用于其它领域的预报当中去.

［1］彭秀艳，王茂，刘长德.AR模型参数应估计方法研究及应用［J］.哈尔滨工业大学学报，2009，41(9): 12-16.

PENG Xiuyan，WANG Mao，LIU Changde.Adaptive estimation method of AR model parameters［J］.Journal of Harbin Institute of Technology，2009，41(9):12-16.

［2］侯建军，东昉，蔡烽.混沌理论和神经网络相结合的舰船摇荡运动极短期预报［J］.舰船科学技术，2008，30 (1):67-70.

HOU Jianjun，DONG Fang，CAI Feng.Extreme short term prediction of ship swaying motions based on combination of chaos and neural network［J］.Ship Science and Technology，2008，30(1):67-70.

［3］VAPNIK V N.The nature of statistical learning［M］.New York:Springer，1995:55-92.

［4］刘胜，李妍妍.基于支持向量机的锅炉过热系统建模研究［J］.热能动力工程，2007，22(1):38-42.

LIU Sheng，LI Yanyan.A study of the modeling of a boiler superheating system based on a supportive vector machine［J］.Journal of Engineering for Thermal Energy and Power，2007，22(1):38-42.

［5］刘胜，傅荟璇，王宇超.基于平面靶分割区间LS-SVM摄像机标定的研究［J］.哈尔滨工程大学学报，2009，30 (10):1117-1122.

LIU Sheng，FU Huixuan，WANG Yuchao.Calibration of multi camera visual systems using divided LS-SVM［J］.Journal of Harbin Engineering University，2009，30(10): 1117-1122.

［6］LUO W L，ZOU Z J.Identification of response models of ship maneuvering motion using support vector machines［J］.Journal of Ship Mechanics，2007，11(6):832-838.

［7］罗伟林.基于支持向量机方法的船舶操纵运动建模研究［D］.上海:上海交通大学，2009:37-51.

LUO Weilin.On the modeling of ship manoeuvring motion by using support vector machines［D］.Shanghai:Shanghai Jiao Tong University，2009:37-51.

［8］江娜.SVM及其在船舶航向控制系统故障预报中的应用研究［D］.哈尔滨:哈尔滨工程大学，2008:94-120.

JIANG Na.SVM and its application to fault prediction of ship heading control system［D］.Harbin:Harbin Engineering University，2008:94-120.

［9］胡根生，邓其飞.具有多分段损失函数的多输出支持向量回归机［J］.控制理论与应用，2007，24(5): 711-714.

HU Gensheng，DENG Qifei.Multi-output support vector regression with piecewise loss function［J］.Control Theory and Applications，2007，24(5):711-714.

［10］肖建，于龙，白裔峰.支持向量回归中核函数和超参数选择方法综述［J］.西南交通大学学报，2008，43(3): 297-303.

XIAO Jian，YU Long，BAI Yifeng.Survey of the selection of kernels and hyper-parameters in support vector regression［J］.Journal of Southwest Jiao Tong University，2008，43(3):297-303.

［11］WEN X J，CAI Y Z，XU X M.Least squares support vector machine based on continuous wavelet kernel［J］.Lecture Notes in Computer Science，2005，3496:843-850.

［12］WU Q.The forecasting model based on wavelet-support vector machine［J］.Expert Systems with Applications:an International Journal，2009，36(4):7604-7610.

［13］刘胜，李妍妍.自适应 GA-SVM参数选择算法研究［J］.哈尔滨工程大学学报，2007，28(4):398-402.

LIU Sheng，LI Yanyan.Parameter selection algorithm for supportvectormachines based on adaptive genetic algorithm［J］.Journal of Harbin Engineering University，2007，28(4):398-402.