四柱结构在波浪作用下的近场干涉

姜胜超，吕林，滕斌，勾莹

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024;2.大连理工大学 深海工程研究中心，辽宁 大连116024)

海洋平台的支撑结构往往由多根立柱构成，这些立柱由于距离较近，相互间水动力影响较强，并会在某些特定的入射波频率下出现复杂的近场干涉现象［1－2］，对结构产生不利影响.对于多桩柱海洋平台而言，它主要体现在以下2个方面:引起桩柱结构上作用压强和波浪力的显著增大［3］，导致平台发生局部破坏甚至整体倾覆;造成平台立柱周围波高的显著增加［4］，如产生波浪上涌或甲板上浪等现象，影响平台的气隙性能并加剧波浪对平台下甲板的冲击.因此，研究多柱结构在发生近场干涉情况下的局部波高分布及结构受力是十分必要的.

水波问题中的近场干涉最早由Simon［5］提出，Maniar和 Newman［3］在研究串列圆柱所受波浪力时，通过理论分析给出了无穷多圆柱情况下的近场干涉发生条件，Evans和Porter［6］基于镜像法进一步研究了双排圆柱群的近场干涉发生条件，发现与单排圆柱情况相比，共振频率分别向高频和低频方向移动.Porter和Evans［7］对近场干涉发生时多圆柱间的波面分布进行了研究，发现其具有明显的对称与反对称特征.McIver［8］对这些早期工作进行了比较全面的总结.在海洋工程中，四圆柱结构的应用非常广泛，但以往的研究工作由于多着重于理论层面，因而对四柱结构周围的水动力干涉问题的研究还相对较少.OHL［9－10］针对一座实际张力腿平台开展了规则波和不规则波作用下平台附近的波浪场变化研究.通过数值结果与实验资料的对比，发现采用线性绕射理论可以获得与实际情况比较符合的数值计算结果.然而，该工作并没有对复杂的近场干涉现象开展深入的研究.Evans和Porter［11－12］基于解析方法研究了有限水深四根坐底圆柱的水动力干涉问题，发现当入射波沿四根圆柱对角线方向入射时，近场干涉现象最为明显，主要体现在每根圆柱都将受到较大的水平波浪力，且其内侧波面也会出现较大的波高.但是，该文献并没有对两者的关系进行深入的探讨.

基于上述成果，对海洋工程中常见的四柱结构的近场干涉问题开展了进一步的研究.揭示圆柱结构周围的波高变化对入射波频率的依赖关系，从局部波高分布特征的角度讨论水平波浪力的产生机制.研究了圆柱所受的二阶漂移力，对其产生机理进行分析.

1 水动力计算的边界元方法

波浪对无限水深中物体的作用问题可视为理想流体的无旋运动(如图1)，此时的流体运动存在速度势Φ(x，t)，在不可压缩假设条件下，质量守恒可通过如下的拉普拉斯方程进行描述:

应用摄动理论，对速度势按波陡ε(ε=kA，k为波数，A为波幅)展开，取一阶近似，对于频率为ω的正弦入射波，可以进一步从速度势中分离出时间因子，写成如下的形式:

式中:φ为空间复速度势，它仍满足拉普拉斯方程.对于固定物体，可将其进一步分解为入射势φi和绕射势φd，即

式中:绕射势φd满足如下的自由水面SF、物面SB及无穷远处边界条件:

式中:g为重力加速度，n为物面法向量(以指出流体为正).

图1 计算域和边界定义图Fig.1 Definitions of computational domain and boundaries

为采用边界元方法对上述问题进行数值求解，取能同时满足自由水面边界条件、无限水深海底条件和远场辐射条件的格林函数为

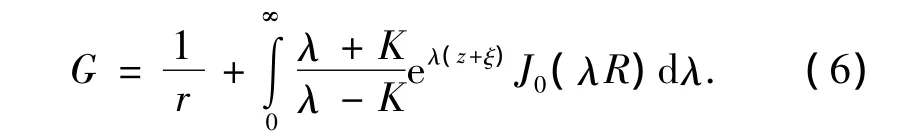
式中:r=［R2+(z－z0)2］1/2;R是场点和源点的水平距离;K=ω2/g是深水波数.对格林函数及速度势应用第二格林定理，可建立边界积分方程:

式中:α为固角系数.在高阶元中，其值随源点x0位置的不同而改变，可根据源点所在单元的几何性质进行求解［13］.采用Teng和Eatock Taylor［14］的方法，在物体内部建立另一个积分方程并与上述方程相结合，进而消除固角系数α和积分方程的奇异性，可以得到一个新的积分方程:

其中，G0为满足刚性自由表面条件的格林函数:

式中:r1=［R2+(z+z0)2］1/2.

根据式可求得绕射势，进而由伯努利方程获得流体压强，通过物体表面的速度势积分可以求得物体受到的一阶波浪力f(1)j及二阶漂移力f(2)j:

式中:Γ为物体与静水面交线，称为水线，*表示取复共轭，式(12)和(13)一般称为近场方法.

结构物在x和y方向的二阶漂移力还可以通过远场方法进行计算:

式中:As(θ)为散射波的远场波面，C和Cg分别为入射波浪的相速度和它所对应的波群相速度.远场方法和近场方法计算结果的对比可以应用于网格收敛性检验.

对于正弦谐波，一阶波面可以表示为

式中:

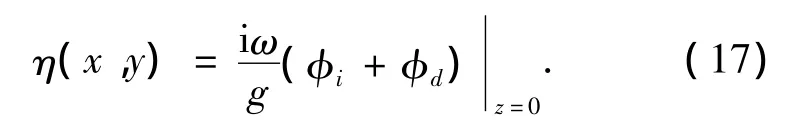
可见，为获得自由水面上的波面分布，必须先求得速度势.式(17)中的入射势φi可根据入射波浪条件直接给出，而对于自由水面上的绕射势φd可通过下述方程求出:

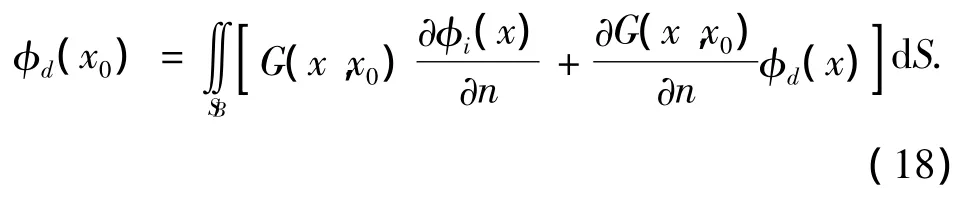
2 数值实验设置及网格剖分

采用上述数值模型对海洋工程中常见的四柱结构在波浪作用下的水动力干涉问题开展数值研究.如图2所示，圆柱半径为a，吃水深度T=3a，圆柱中心轴线分别位于和处，相邻圆柱轴线间的距离为4a，转动中心固定于坐标原点，水深为无限水深，波浪沿x轴正方向入射.为了提高波面计算精度，采用较密的网格剖分形式，如图3所示，其中，每个圆柱表面剖分672个单元(环向为32个，垂向为15个，柱底径向为6个)，在进行波面计算时，自由水面使用非结构化四边形网格8 300个.为了验证所选网格的收敛性，分别采用前述的远场方法和近场方法对四柱结构在水平方向上的二阶漂移力进行了计算，比较结果如图4所示.从图中可以看出，2种方法的计算结果相互符合，说明目前的网格剖分可以应用于后文的数值计算.

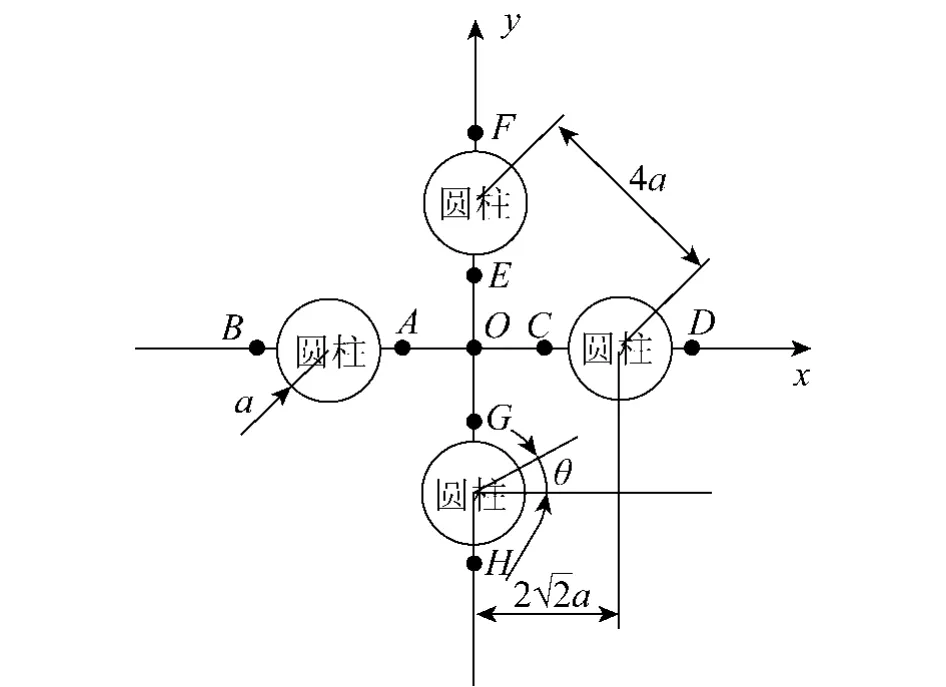
图2 波浪作用下的四柱结构Fig.2 Four-cylinder structure in regular wave

图3 四柱结构的物面与自由水面网格剖分Fig.3 Sketch definition of four-cylinder structure and the mesh generation

图4 远场方法和近场方法的二阶漂移力比较Fig.4 Comparison of the second order drift force by far field and near field methods

3 结构附近的波浪分布

3.1 结构附近波高与入射频率的关系

为了研究上述四柱结构附近波高随入射波频率的变化情况，在每根圆柱内外两侧距圆柱中心1.1a处共选取8个测点以记录其波高变化，测点编号位置及具体坐标分别参见图2及表1.

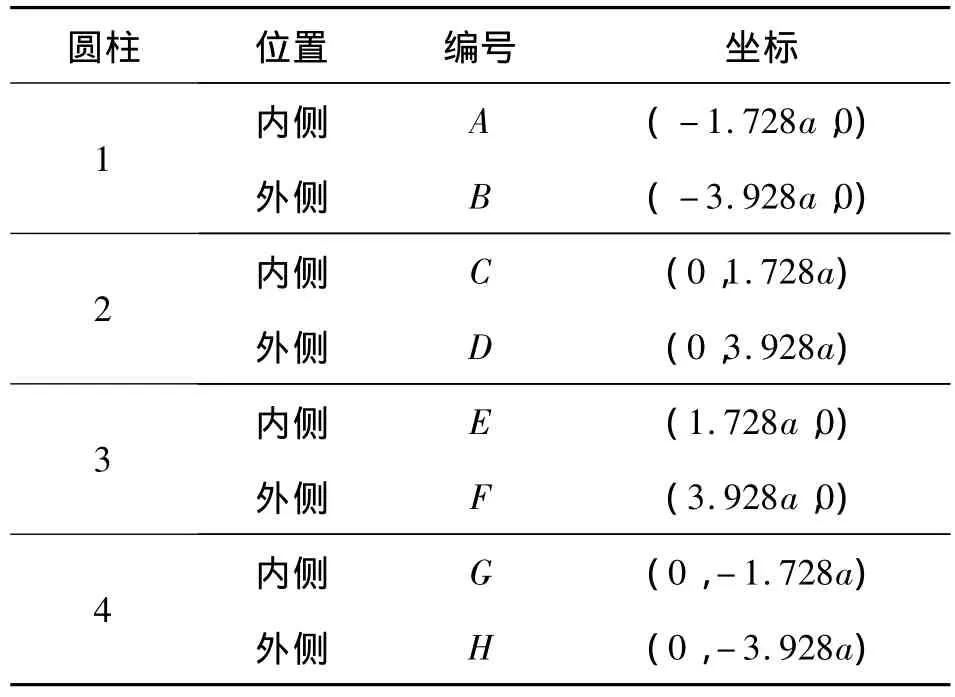
表1 结构附近波高测点的坐标值Table 1 Coordinates of test points near four-cylinder sturcture

图5(a)为圆柱1内外两侧测点A和B处波高随频率的变化曲线，可以看出，由于圆柱1直接暴露于入射波浪的作用之下，其附近波浪场较为复杂，两测点A和B处的波高随入射波频率的变化具有明显的振荡特征.在绝大多数频率下，由于测点B处于迎浪侧，其无因次波高均大于测点A.当ka=1.68时，圆柱1的内测点出现波浪叠加，流体发生共振运动，测点A处的波高出现一个较大的峰值，同时，外测点B处的波高在其附近也出现一个较大的峰值，但低于测点A的波高，这是由于发生近场干涉时，波能向圆柱内侧聚集，波高相应增大，而外侧波能有所降低所致.

与圆柱1附近测点A和B相比，圆柱2外侧测点D处的波高随入射波频率的变化相对较弱，且始终维持在一个较低水平，如图5(b)所示.这是由于该测点位于四柱结构的背浪侧，受圆柱群的遮挡效应较为明显.当ka=1.68附近时，圆柱2内侧测点C处的波高出现一个明显的峰值，同时其外侧测点D处的波高在该频率附近也出现少量增加.

对于圆柱3和4而言(两者具有空间对称性)，如图5(c)所示，其内侧测点E和G处的波面在ka=1.68附近出现峰值，而外侧测点F和H则出现谷值，这同样是由于近场干涉发生时，波能向圆柱内侧集中，使得内侧波高明显增大.所不同的是，此时圆柱外侧的波能大量转移到内侧，从而使外测点F和H处的波高出现明显降低.

将图5(a)～(c)中圆柱内侧测点，即A、C、E和G处的波面峰值进行比较，可以看出，位于背浪侧的圆柱3内侧测点C处的波面最大，圆柱2和4内侧测点E和G次之，而处于迎浪侧圆柱1的内侧测点A处的波面则最低.对于圆柱1的内测点A而言，它位于圆柱1的下游，由于受到圆柱1的遮挡作用，传播到此处的波能相对较少，因此波高偏小.而对于圆柱3的内测点C而言，它位于圆柱3的上游，波能传播到此后受圆柱3的阻碍发生滞留，同时由于波浪多次反射产生叠加，故使得该测点处的波高相对较大.而圆柱3和4的内侧测点E和G则居于两者之间，则充分反映了来自圆柱本身的遮蔽和阻碍作用对局部波高的影响.

图5 圆柱内外两侧测点处波高随频率变化对比图Fig.5 Variation of wave heights at typical points with incident wave frequency

为了进一步明确四柱结构内部的波浪状况，在此给出其中心点O(0，0)处的波高随入射波频率的变化情况，如图6所示.从图中可以看出，在大多数频率下，四柱结构中心点处的无因次波高基本维持在1左右，最大波高出现在ka=0.50附近，其值仅为1.62，这相对于前述的内测点A、C、E和G而言，波高明显偏小.当ka＞2.3之后，该测点处的波高出现明显的下降趋势，这是由于在短波的反射作用较强，传播到此处的波能较少的缘故.最后，在圆柱内侧波高较大的波数ka=1.68附近，结构中心O点处的波高并没有发生明显的变化，因此，近场干涉对平台气隙性能的影响将主要体现在桩柱附近.

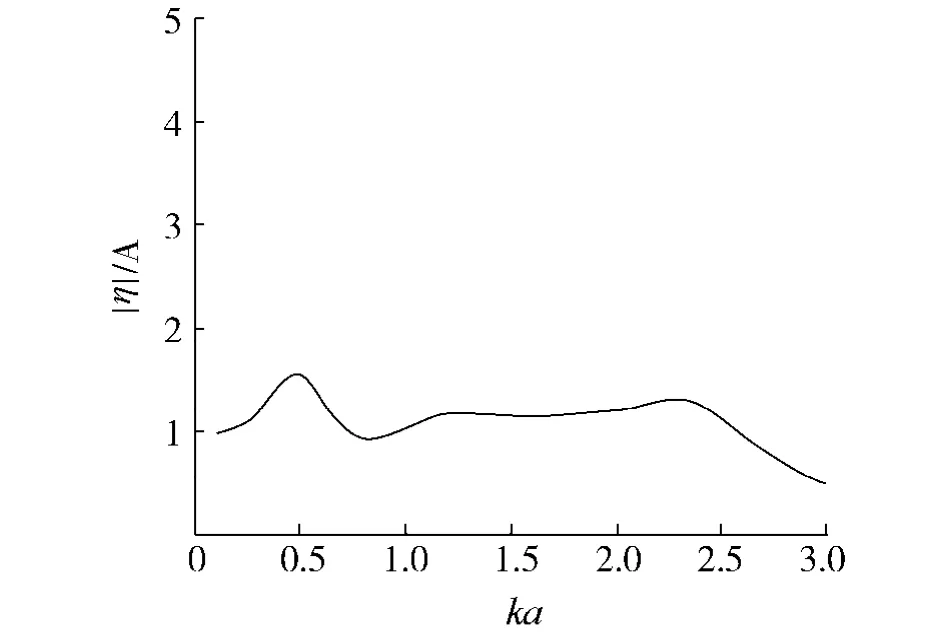
图6 四柱结构中心处波高随频率变化对比图Fig.6 Variation of wave height at the center of four-cylinder structure with incident wave frequency

3.2 圆柱表面的波浪爬高

如前所述，当发生近场干涉时，波浪会在圆柱附近产生爬高，这对分析平台的气隙性能非常重要.前文对圆柱附近几个代表位置处的波高随入射波频率的变化进行了分析.为清楚了解波浪的爬高情况，对ka=1.68时圆柱结构周围的波高总体分布进行分析，结果如图7所示.其中，角度θ的定义参见图2.对于圆柱1而言，最大爬高出现在圆柱内外两侧，但内侧爬高略大，且影响范围较宽，波浪爬高随角度θ呈“W”形的分布.对于圆柱2而言，最大波浪爬高出现在圆柱内侧，外侧的爬高并不明显，波浪爬高分布与角度θ呈倒“V”形关系.由于波浪在圆柱2的内侧经多次反射后发生叠加，与其他圆柱相比，其波浪爬高相对最明显，约为入射波高的4.2倍.另外，从图7(b)中还可以看出，圆柱2外侧的最小波浪爬高并未出现在完全背浪点处，而是出现在背浪点±35°左右的位置，这是绕射波在结构物后方相互干涉的结果.对于圆柱3和4而言，由于入射波浪的作用，最大和最小的波浪爬高并没有恰好出现在圆柱内外两侧，而是分别出现在85°和275°的位置，总体上向下游漂移.

3.3 总波面分布

图8进一步给出了相对波数分别为ka=1.00、1.68和2.00时四柱结构周围的无因次波高分布图，可以看出，由于入射波与反射波的叠加，四柱结构整体的前方波高普遍较大，且呈现出明显的驻波波态，而在结构物的后方由于遮挡效应明显，波高相对较低.将3种情况进行对比，可以看出，当ka=1.00时，结构物后方的波高较大，这是因为入射波浪的波长较长，而长波穿透能力较强，有较多的波能可以绕射到四柱结构的后方.当ka=2.00时，由于波长较短，透射能力差，反射作用明显，相对于ka=1.00的情况，波浪传播到结构物后方的能量较少，因此波高较小.而当ka=1.68时，近场干涉现象发生，波能向圆柱周围集中，导致其附近的波面发生大幅抬升，而远场区波面则普遍较低.特别是在四柱结构后方出现一个明显的小波高分布区域，且向下游延伸的范围较大，这一现象与单排柱群在顺浪作用时的Neumann共振模态是类似的［15］.

图8 不同频率时四柱结构周围的波面分布Fig.8 Wave distribution around four-cylinder structure

4 物体所受到的波浪作用力

4.1 一阶波浪力

4.1.1 每根圆柱所受一阶波浪力

为了研究四柱结构的受力特征，对不同频率下各圆柱受到的波浪力进行了计算，并与单根圆柱时的情况进行对比.对于水平力而言，从图9中可以看出，在低频区，波浪场受结构物的影响较弱，作用在每根圆柱上的水平波浪力都接近于单根圆柱时的情况.而在高频区，由于结构物对波浪场的影响作用开始明显，圆柱所受波浪力与单根圆柱的情况相比出现较大的差别，并在圆柱周围出现大幅波动的频率附近出现较大的振荡变化.就水平波浪力的峰值而言，圆柱1的波浪力峰值最大，圆柱2次之，而圆柱3和4则较小(图9中所示为水平方向的合力).实际上，圆柱所受波浪力的大小与其周围的波浪条件密切相关.例如，对于圆柱2而言，当近场干涉发生时，圆柱内侧波高较大，而外侧波高则维持在一个较低水平，因此其受到的水平波浪力明显增大.对于圆柱1而言，虽然其前后两侧波高相差较小，但它们相位相差较大(参见图10)，因此波浪力也较大.综合而言，对于圆柱1和2而言，其水平波浪力的幅值变化主要受到圆柱周围波高分布的影响，并且与相位关系密切.

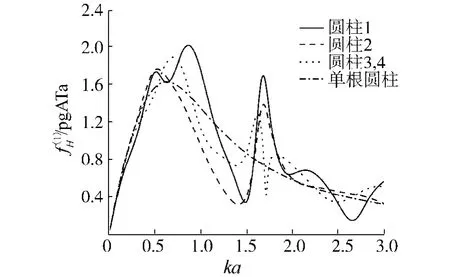
图9 圆柱所受到的水平波浪力Fig.9 Horizontal wave force on cylinder

与圆柱1和圆柱2具有空间对称性不同，圆柱3和4的水平波浪力具有x和y2个方向的分量，如图11所示.可以看出，当频率较低时，圆柱在y方向受力很小，而x方向波浪力接近于单根圆柱时候的情况.随着入射波频率的增加，波浪场受结构物的扰动作用逐渐增强，圆柱在y方向受到的波浪力逐渐显现出来，并在ka=1.68时出现一个较大的峰值，且该峰值所对应的频率恰好也是圆柱3和4的总水平波浪力峰值所对应的频率.近场干涉发生作用在圆柱3和4上的水平波浪力主要受其周围自由水面分布情况的控制.参见图8可知，圆柱3和4最大的波高差异出现在其内外两侧，而不是其迎浪测与背浪侧，因此y方向波浪力分量较大.从总体上而言，圆柱3和4的总水平波浪力主要受x方向分量的控制，但在近场干涉条件下，y方向分量的影响不容忽视.

图10 圆柱1和2内外两侧测点处相位随频率变化对比图Fig.10 Wave elevation near cylinders 1 and 2 with incident wave frequency

图11 圆柱在波浪作用下受到的垂向力Fig.11 Vertical wave force on cylinder

图11所示为每根圆柱所受垂向力随频率的变化关系，可以看出，圆柱垂向力在低频范围的影响较大，且随ka的增加而迅速降低，而在高频时基本为零.在绝大多数情况下，圆柱1所受垂向力最大，圆柱3和4次之，而圆柱2所受垂向力最小，这是由于物体的垂向力主要由波浪与结构物作用时的动水压力提供，圆柱1直接暴露在入射波的作用下，因此由波浪的运动所产生的动水压力变化幅值也较大，而圆柱2受到其他圆柱较好的遮蔽作用，入射波浪与其之间的相互作用相对较弱，故对应的垂向力也相对较低，圆柱3和4则居于两者之间.总体上讲，四根圆柱所受垂向力与单根圆柱的情况相类似.

4.1.2 四柱结构所受一阶总波浪力

一般来说，海洋平台(如TLP平台)的四根柱状浮筒通常使用浮架连接，因此，作用在桩柱上的总波浪力也是工程中非常关注的问题.为便于和单根圆柱的情况进行对比，将总波浪力f(1)用平均值表示，即，如图12所示.从图12(a)中可以看出，与每根圆柱的受力特征不同，在相对波数ka=1.68附近，物体在水平方向上的总波浪力并没有出现极大值，近场干涉并未导致四柱结构的总水平波浪力出现明显增加.相反，在四柱情况下，作用在圆柱单体上的平均水平波浪力要明显低于单根圆柱的情况，这主要是由于各圆柱上的波浪力之间存在相位差，总体上相互抵消的缘故，这对群桩的整体安全性是有利的.同时，四柱结构所受到的平均垂向波浪力也低于单根圆柱时候的情况.因此，近场干涉现象并不会对结构物的整体作用力产生不利的影响.

图12 四柱结构在波浪作用下受到的波浪力Fig.12 Wave force on four-cylinder structure

4.2 二阶漂移力

4.2.1 每根圆柱上的二阶漂移力

图13，14为每根圆柱所受到的水平二阶漂移力随频率的变化关系，与一阶波浪力的情况相似，圆柱所受二阶漂移力在ka=1.68附近出现了一个较大的峰值.从图中可以看出，当ka=1.68时，圆柱2和圆柱3所受水平漂移力为正，而圆柱1和圆柱4所受漂移力为负，因此二阶漂移力的方向为由内指向外，使每根圆柱均具有向外侧漂移的趋势.相比之下，圆柱2的水平二阶漂移力最大，圆柱3和4次之，而圆柱1则最小，这是由于圆柱2前后的波面差异最大，非线性漂移作用较强的缘故.

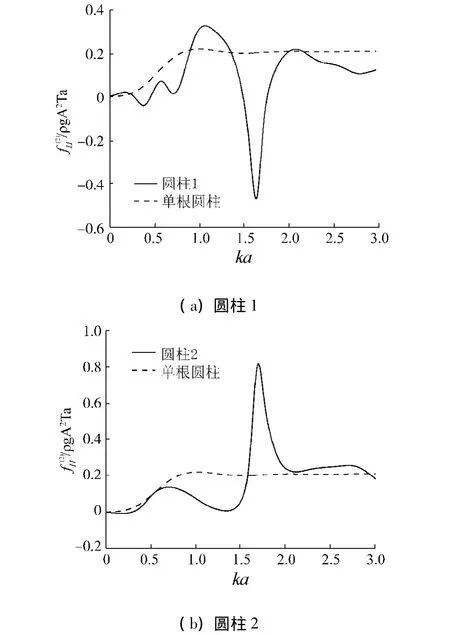
图13 圆柱2在波浪作用下的二阶漂移力Fig.13 Mean drift force on cylinder 1，2

对于圆柱所受到的垂向二阶漂移力而言，如图15所示，可以看出，圆柱垂向漂移力在低频范围对波数ka的依赖作用明显，在高频则基本为零，垂向漂移力的最大值峰值(绝对值)出现在ka=0.20附近，但其值均小于单根圆柱时候的情况.相比而言，圆柱2受力最小，圆柱1次之，而圆柱3和4最大.

4.2.2 结构所受总二阶漂移力

与讨论一阶波浪力时的方法相同，将四柱结构所受总二阶漂移力用每根圆柱所受到的平均二阶漂移力来表示，即，如图16所示.对于水平力而言，总体上而言，四柱结构的平均二阶漂移力基本上在单根圆柱漂移力曲线附近上下震荡，差别并不是很大，如图16(a)所示，这同样是由于近场干涉发生时，每根圆柱所受到的漂移力的方向为由内指向外，彼此间相互抵消的缘故.而对于垂向力而言，如图16(b)所示，四柱结构的整体漂移力基本小于单根圆柱时候的情况.总之，无论是水平方向，还是垂直方向，近场干涉均未对其二阶漂移力产生非常重要的影响.

图14 圆柱3在波浪作用下的二阶漂移力Fig.14 Mean drift force on cylinder 3

图15 每根圆柱波浪作用下的垂向二阶漂移力比较Fig.15 Vertical mean drift force on each cylinder

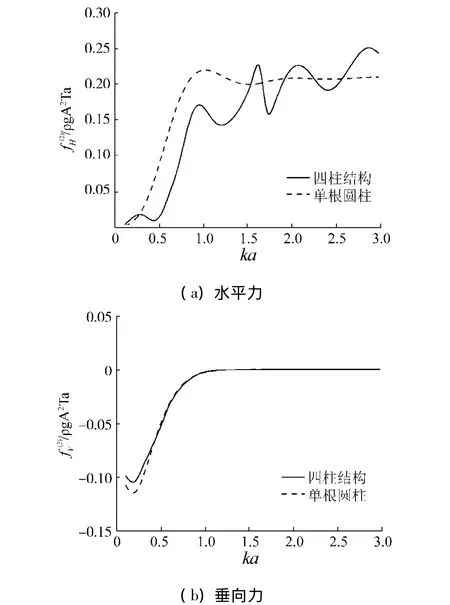
图16 四柱结构在波浪作用下受到的漂移力Fig.16 Drift forces on four-cylinder structure

5 结束语

采用数值方法，对海洋工程中常见的四柱结构的近场干涉现象进行了研究.结果表明，当发生近场干涉时，波能向结构物内侧集中，流体发生共振运动，圆柱周围的波高出现大幅增加，可达入射波的4倍，而四柱结构内部中心区域的波高则始终维持在一个较低的水平.各圆柱所受水平一阶波浪力在近场干涉频率附近也发生明显变化，水平波浪力的幅值主要受圆柱周围波高分布和相位变化的控制.就四柱结构的总水平波浪力而言，近场干涉现象对其影响作用有限，在大多数波浪条件下均低于孤立圆柱的四倍.对于二阶水平漂移力而言，在近场干涉发生时，作用在各个圆柱上的二阶漂移力迅速增大，但在总体上相互抵消，使得四柱结构整体受到到的漂移力类似于孤立圆柱的情况.对于作用在四柱结构上的垂直力而言，一阶波浪力和二阶漂移力均与孤立圆柱的情况比较接近.应该说明的是，由于研究工作是在势流理论范畴内开展的，对近场干涉问题而言，圆柱近壁区的流体粘性阻尼和能量耗散有可能对波高变化起到一定作用，更深入的研究工作需要借助Navier－Stockes方程数值求解来实现.但对于了解近场干涉的基本现象和物理规律是有意义的.

［1］NEWMAN J N.Wave effect on multiple bodies［M］.［s.l.］:Hydrodynamics in Ship and Ocean Engineering，2001: 3－26.

［2］DUCLOS G，CLEMENT A H.Wave propagation through arrays of unevenly spaced vertical piles［J］.Ocean Engineering，2004，31:1655－1668.

［3］MANIAR H D，NEWMAN J N.Wave diffraction by a long array of cylinders［J］.J Fluid Mech，1997，339:309－330.

［4］MOLIN B.On the piston and sloshing modes in moonpools［J］.J Fluid Mech，2001，430:27－50.

［5］SIMON M.Multiple scattering in arrays of axisymmetric wave－energy devies，Part 1.a matrix method using a planewave approximation［J］.J Fluid Mech，1982，120:1－25.

［6］EVANS D V，PORTER R.Trapped modes about multiple cylinders in a channel［J］.J Fluid Mech，1997，339:331－356.

［7］PORTER R，EVANS D V.Rayleigh－Bloch surface waves along periodic gratings and their connection with trapped modes in waveguides［J］.J Fluid Mech，1999，386:233－258.

［8］MCIVER P.Wave interaction with arrays of structures［J］.Applied Ocean Research，2002，24:121－126.

［9］OHL C O G，EATOCK TAYLOR R，TAYLOR P H，et al.Water wave diffraction by a cylinder array.Part 1.regular waves［J］.J Fluid Mech，2001，442:1－32.

［10］OHL C O G，EATOCK TAYLOR R，TAYLOR P H，et al.Water wave diffraction by a cylinder array.Part 2.Irregular waves［J］.J Fluid Mech，2001，442:33－66.

［11］EVANS D V，PORTER R.Near trapping of waves by circular arrays of vertical cylinder arrays［J］.Journal of Fluids and Structures，1991，5:1－32.

［12］EVANS D V，PORTER R.Tapping and near－trapping by arrays of cylinders in waves［J］.Journal of Engineering Mathematics，1999，442:33－66.

［13］TENG B，GOU Y，NING D Z.A higher order BEM for wave－current action with structure－directory computation of free－term coefficient and CPV intergrals［J］.China Ocean Engineering，2006，20(3):395－410.

［14］TENG B，EATOCK TAYLOR R.New higher－order boundary element methods for wave diffraction/radiation［J］.Applied Ocean Research，1995，17(2):71－77.

［15］WALKER D A G，EATOCK TAYLOR R.Wave diffraction from linear arrays of cylinders［J］.Ocean Engineering，2005，32:2053－2078.