随机阵列误差影响下的声矢量阵噪声特性和阵增益

刘凯，梁国龙，嵇建飞，张锴

(哈尔滨工程大学 水声技术国家级重点实验室，黑龙江 哈尔滨 150001)

声矢量阵被应用于实际声呐系统的例子已屡见不鲜［1-2］.相对于标量阵，声矢量阵突显出来的优势得到众多学者的证明［3-4］.然而很多优势都是在理想的假设条件下取得的，随机阵列误差的存在可能使得这些假设不再成立.对于声矢量阵，主要的随机阵列误差包括信号通道的幅相误差、阵元位置误差和阵元姿态误差等.

一切声呐系统的灵魂应该是它采用的核心算法.判断算法在某特定噪声环境中的性能优劣，评定其鲁棒性的强弱，是指导算法设计的重要环节.不比标量阵［5-6］，目前有关随机阵列误差影响下声矢量阵算法性能分析的文献还尚不多见.于是尝试性的做了下列工作:1)建立了随机阵元位置误差和阵元姿态误差的高斯扰动模型;2)推导了随机阵列误差影响下声矢量阵的噪声时空相关矩阵;3)推导了MVDR波束形成器实际阵增益的解析表达式，找出了导致阵增益出现衰减的直接因素，即畸变后的噪声协方差矩阵和失配的导向向量;4)结合“等间距布放的声矢量直线阵”实例，分析了随机阵列误差对噪声相关系数的影响，并考察了实际阵增益在不同的阵列误差强度、训练数据的信噪比以及阵元间距下的统计特性.

1 阵列误差的高斯扰动模型

阵列误差可分为2类:可预测的和随机的.可预测的误差可通过估计和补偿消除，随机误差是很难补偿的，因而成了限制阵列系统性能的最终因素.Gauss在研究误差理论时发现随机误差服从的分布为正态分布(后来又称为高斯分布).

1.1 阵元位置误差模型

假设声矢量阵的第m号基元的初始位置为

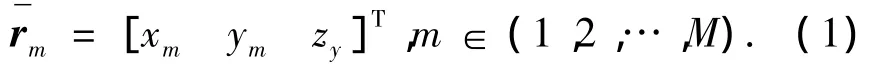
受内波、浪涌和母船激起的水流等因素的影响，基元会作一种无规则的随机扰动.在高斯扰动模型下，第m号基元的实际坐标变为

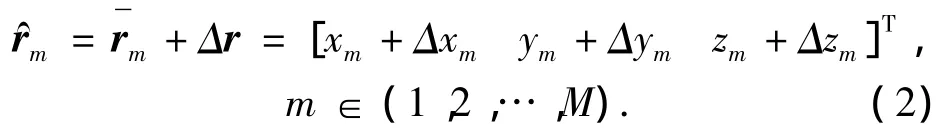
式中:Δxm、Δym和Δzm为扰动分量，三者统计独立并且Δxm、Δym、ΔzmN(0，σ2r)，其中σr为标准差，并定义σλ=(2π/λ)σr.

1.2 阵元姿态误差模型

理想条件下，可以先通过方位姿态仪等测量仪器精确获取基元的姿态参数(heading，pitch，roll)，然后旋转其输出使之与坐标轴对齐［4］.在平面波的假设下，各基元的方位响应都能够表示为

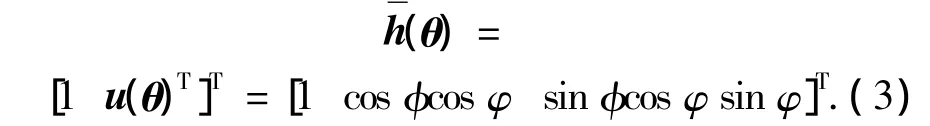
式中:θ=［φ φ］T为声源的入射方向(φ为方位角，φ∈(0，2π］);φ是俯仰角为矢量传感器所在点指向目标声源的单位方向向量.

在实际应用中，受方位姿态仪的测量精度、安装偏差、平台的电磁场以及因水流冲刷而快速旋转等因素的影响，测得的姿态参数会存在误差.在运动学上，广义欧拉角是最常用的描述刚体旋转状态的方法［7］.为了表述阵元姿态误差，建立了定坐标系Oξηζ和与矢量传感器相固结的体坐标系Oxyz，并将原点O取在矢量传感器的质点上，如图1所示.

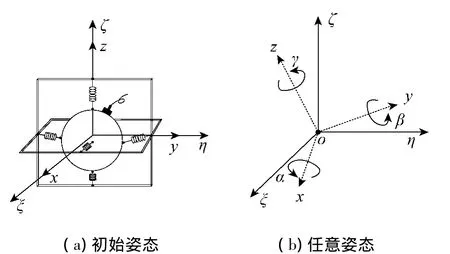
图1 广义欧拉角表示阵元姿态误差Fig.1 Attitude errors represented by generalized Euler Angle

矢量传感器处于初始姿态时，体坐标系Oxyz与定坐标系Oξηζ重合.其他任意姿态都可通过3次顺序转动获得:1)绕z轴转Δγm角;2)绕体轴y(在新位置)转Δβm角;3)绕体轴x(在新位置)转Δαm角，3个转角(Δαm，Δβm，Δγm)统称为广义欧拉角.包含了阵元姿态误差的方向余弦矩阵ΔΞm通过下式用广义欧拉角表示:

式中:cΔαm、sΔβm为cosΔαm、sinΔβm的简写.在高斯扰动模型下，第m号基元的方向响应变为

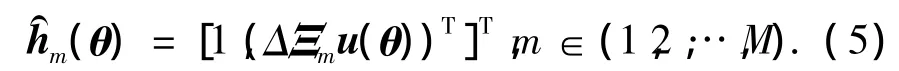
式中:Δαm，Δβm和Δγm表示侧倾、俯仰和横摆等扰动分量，三者统计独立且有Δαm，Δβm，Δγm·N(0，)，其中σξ为标准差.

2 噪声时空相关性分析

海洋环境噪声是声呐设备的背景干扰之一，阵列信号处理算法的设计及性能分析与噪声协方差矩阵密切联系［8］.噪声类型主要包括空间白噪声、方向性噪声(或称干扰)和球面各向同性噪声等.其中空间白噪声在传感器内部噪声起主要作用时才被认为是有效的，后2种噪声类型是更合乎实际应用［9］.文献［10-11］中分析了理想条件下球面各向同性噪声中声压和质点振速的相关性结构，下面分析随机阵列误差影响下的噪声时空相关性.

2.1 方向性噪声

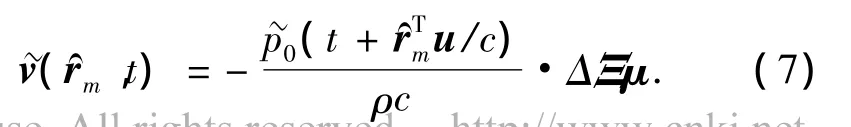
式中:ρ为介质的密度.

将该矢量传感器在t时刻的输出写成以下形式

式中:ρc为波阻抗.假设噪声为零均值的宽平稳随机过程，则(t)的自相关函数可表示为

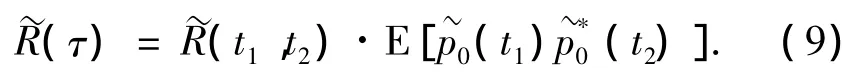
在t1和t2时刻，位于处和处的两矢量传感器之间的时空互相关矩阵可表示为

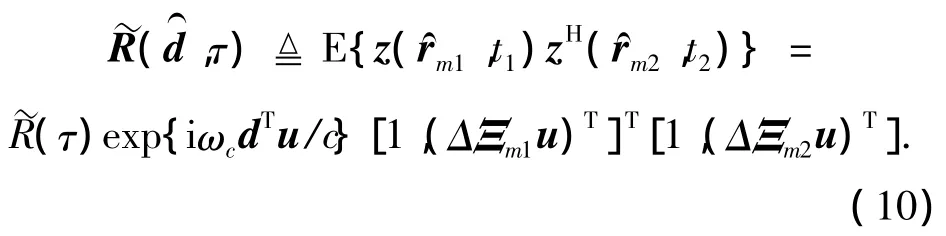
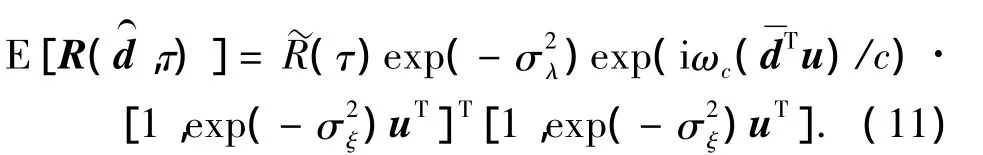
2.2 球面各向同性噪声

采用的模型和假设与文献［9］中的一致，只是加入了随机阵列误差的影响.

推导得出单矢量传感器输出噪声的相关矩阵为

两矢量传感器输出噪声之间的时空互相关矩阵可表示为

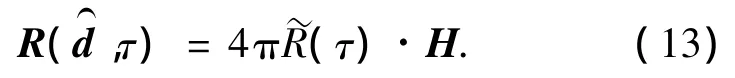
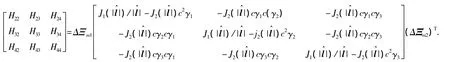
从(12)、(13)式可看出，对于单矢量传感器，各分量之间的相关性并不受阵元姿态误差的影响，仍能保持原有的特性，即所有分量的自相关函数具有相同的瞬时结构，且声压通道的噪声功率为振速通道噪声功率的3倍.对于两矢量传感器的输出，阵列误差会改变所有分量之间互相关系数的数值大小，但不会改变其“奇偶虚实性”.

实例分析:某声矢量直线阵，基元个数为M，处于球面各向同性噪声场中.理想情况下，各基元等间距(阵元间距为)排列，阵元姿态可精确获取.图2给出了此时两矢量传感器相同分量之间的相关系数(CP－P，CVx－Vx，CVy－Vy和CVz－Vz)，以及声压分量分量之间的相关系数恒等于0，故没有一并显示在图上.从图中看出，所有相关系数都随阵元间距的增加而减小;CVx－Vx和CVy－Vy两条曲线完全重合，说明它们受阵元间距大小的影响一样;当阵元间距d≈0.95λ或1.5λ时，CP－P、CVx－Vx和CVy－Vy的值都接近0，说明在此间距下由二维矢量直线阵(如DIFAR阵)的噪声协方差矩阵近似为对角阵.

假设此阵列受阵元位置误差影响，且设定标准差σr=0.1λ，图3(a)和图3(b)分别显示的是CP－P，CVx－Vx，CVy－Vy和CVz－Vz以及CP－Vz的均值和标准差的大小.从图3(a)看出，各相关系数均出现了衰减，衰减程度与原相关系数的绝对值大小成正比.在图3(b)中，CP－P的标准差在附近出现峰值，显然此间距对声压阵的性能很不利，布放阵列时与z轴振速分量之间的相关系数(CP－Vz)随阵元间距的变化规律(已用CP－P进行了归一化处理)，其他应慎重考虑;在任意阵元间距下，CVx－Vx、CVy－Vy都具有相同的统计特性且标准差要低于其他的相关系数，说明它们受阵元位置误差的影响一致且最小.

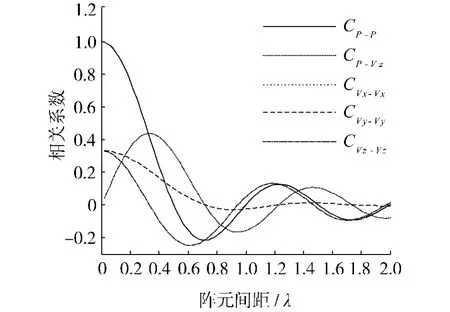
图2 理想条件下的相关系数Fig.2 The ideal correlation coefficient

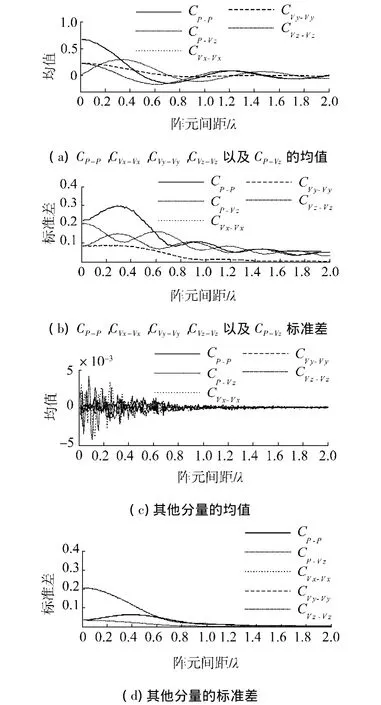
图3 阵列位置误差影响下的相关系数Fig.3 The correlation coefficient influenced by position errors

图3(c)和图3(d)给出了其他分量之间相关系数的均值和标准差.从图3(c)可知，所有原来等于0的相关系数现在已不再为0，其绝对值很小，几乎都能控制在0.004以内.但图3(d)给出的标准差较大，与图3(b)给出的标准差差不多在一个数量级上.

假设此阵列受阵元姿态误差的影响，且设定标准差σξ=20°.图4(a)和图4(b)分别给出了CP－P，CVx－Vx，CVy－Vy，CVz－Vz以及CP－Vz的均值和标准差的大小.从图4(a)中可看出CP－P不受阵元姿态的影响，其他4个相关系数的衰减程度也较小;原来重合的两条曲线CVx－Vx和CVy－Vy，已分开，说明阵元姿态误差对各振速分量的影响不一致.观察图4(b)会发现，CVx－Vx、CVy－Vy、CVz－Vz的标准差随阵元间距的变化趋势十分接近，而且阵元间距较小时标准差较大，说明小间距布放时它们对阵元姿态误差更为敏感.

图4 阵列姿态误差影响下的相关系数Fig.4 The correlation coefficient influenced by attitude errors

其他分量之间相关系数的均值和标准差被显示在图4(c)和图4(d)中.如同图3(c)、图4(c)给出的均值大小也几乎不会超过0.004;图4(d)中的标准差要比图4(b)中的大，因此这些原来等于0的相关系数可能会成为阵列系统性能波动的主要因素.

3 矢量阵阵增益损失分析

3.1 矢量阵测量模型

阵增益能反映波束形成器抑制噪声和干扰的能力，是评价波束形成器性能优劣的重要指标.

MVDR具有优于CBF的阵增益［12］.但在阵列误差的影响下，MVDR的阵增益会急剧下降，甚至可能比CBF的阵增益还低.

假设观察方向为θ0，窄带假设条件下矢量阵的阵列输出可表示为

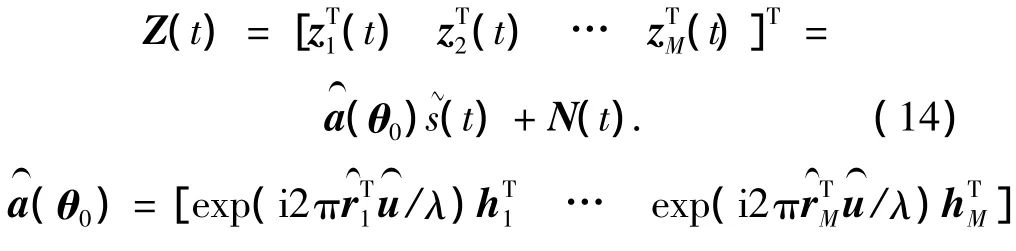
式中:Σs和Σn分别为信号和噪声的协方差矩阵，Jn为归一化的噪声协方差矩阵，可通过式(10)或者式(12)与式(13)计算得到=E［s~(t)s~*(t)］表示输入信号的功率为输入噪声的功率;定义输入信噪比为

令权矢量为W，对阵列输出加权求和，得到矢量阵波束形成器的输出为

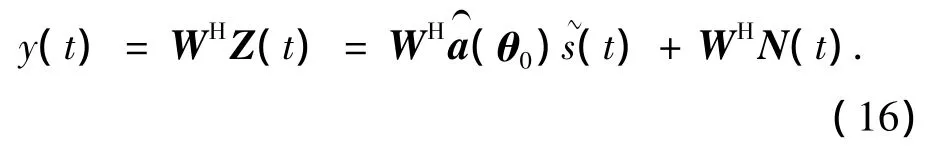
进而求得波束输出功率为

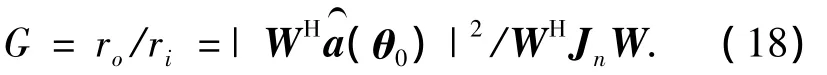
从式(18)中可看出，阵增益不仅受实际的导向矢量a(θ0)和归一化的噪声协方差矩阵Jn的影响，而且与权矢量有关.MVDR的权矢量［4］为

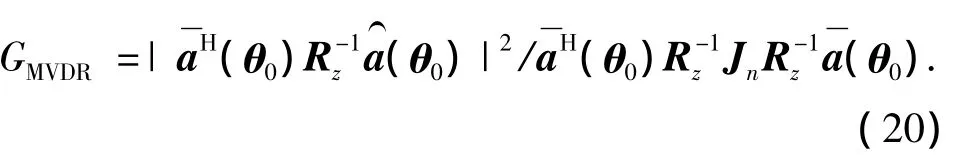
3.2 阵增益损失分析

利用Woodbury矩阵求逆公式得Rz的逆为

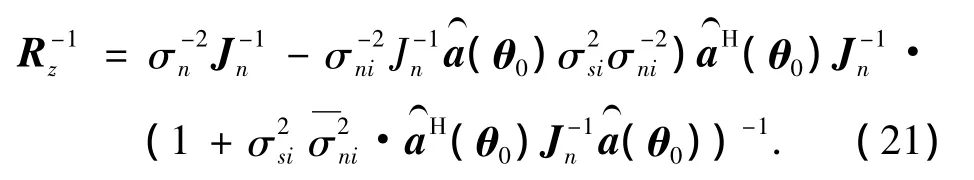
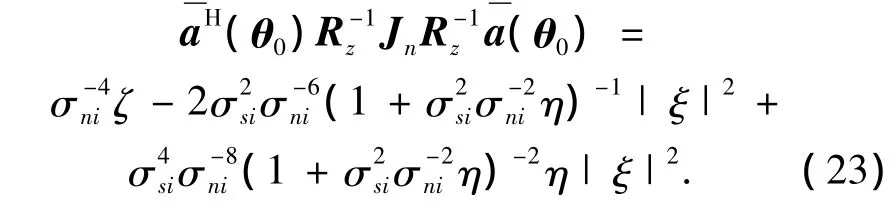
将式(22)、(23)代入式(20)，得到实际的阵增益为

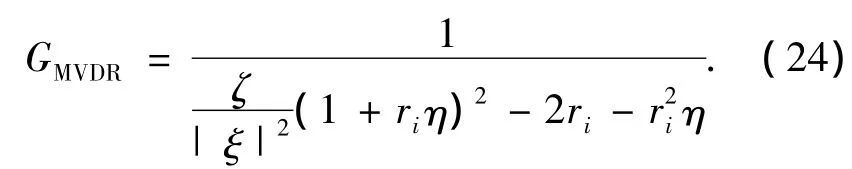
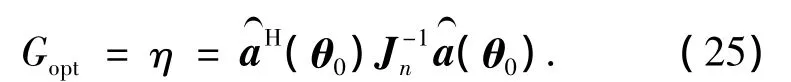
定义

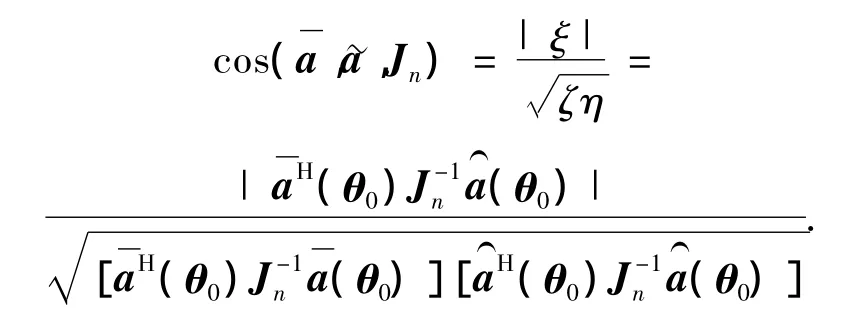
则式(24)可写为

从式(26)看出，总有Gmvdr≤Gopt.阵列误差破坏了Jn包含的噪声相关性结构，并引起和之间的失配，导致阵增益的损失.阵列误差的强度越大，失配就越明显的值就会越大，阵增益的损失也就越严重;在失配程度一定的情况下，输入信噪比越小，阵增益受阵列误差的影响就越小，MVDR的稳健性也就越高.

实例分析:某声矢量直线阵，垂直布放，基元个数M=12，阵元间距首先假设阵列处于方向性噪声场中，3个方向性噪声分别来自［0－30］T，［0 0］T和［0 60］T的方位，功率依次为10、5和0 dB(相对于0 dB的高斯白噪声);总输入信噪比ri设为－20 dB.图5(a)和图5(b)给出了阵元位置误差强度变化时阵增益的统计特性(集平均和标准差);图5(c)和图5(d)给出了阵元姿态误差强度变化时阵增益的统计特性.

从图5可看出，当观察方向远离各噪声入射方位时，阵增益基本上维持在一定值;而一旦接近某噪声入射方位，阵增益会明显下降，而且该方位的噪声功率越大，阵增益下降得越严重.MVDR的设计原理是“让观察方向的信号无失真的输出，而使波束输出总功率最小”，当观察方向靠近噪声方向时，噪声会被误当做信号而无失真的输出，引起阵增益的衰减.同时看出，不管是阵列位置误差还是阵元姿态误差，随着其强度的增大，阵增益都会逐渐变小，其标准差也会相应升高，并在噪声入射方位附近升高得较为明显，说明此时系统的稳健性较差.通过对比发现，阵增益对阵列位置误差的影响更为敏感.这是因为阵元姿态误差只能影响到阵列输入信号的幅度，而阵元位置误差会同时改变其幅度和相位的大小.接着考察阵列处于球面各向同性噪声场中的情形.假设各向同性噪声的功率为20 dB(相对于0 dB的高斯白噪声)，ri仍设为－20 dB.图6(a)和6(b)分别给出了不同强度阵元位置误差影响下阵增益的统计特性，图6(c)和图6(d)给出了不同强度阵元姿态误差影响下阵增益的统计特性.

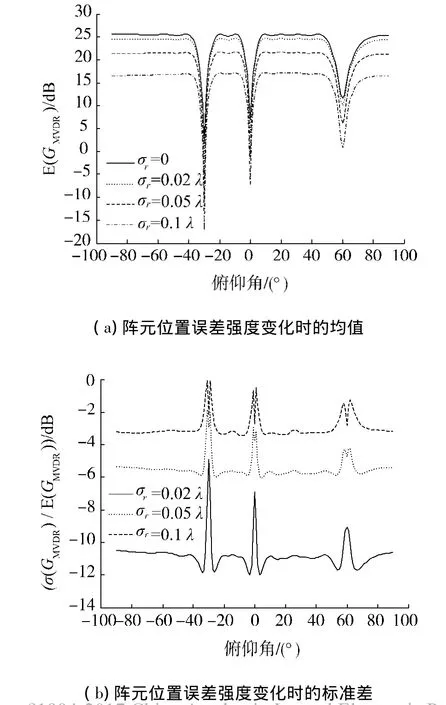
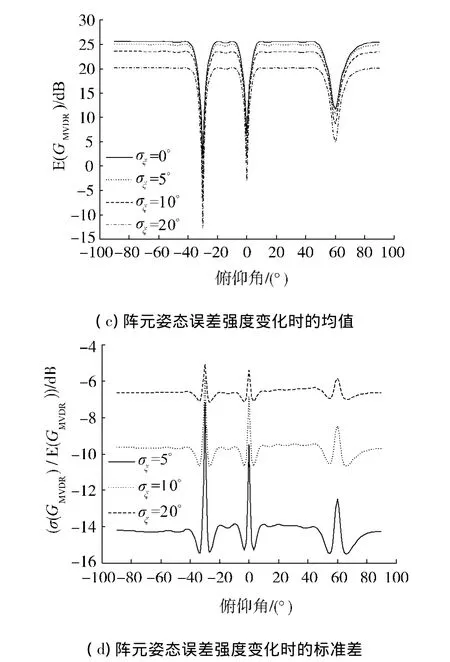
图5 方向性噪声场中的阵增益Fig.5 Array gain in directional noise field

从图6可以看出，在理想条件下，当观察方向位于区间［－50°，50°］时，阵增益与白噪声背景下获得的阵增益相似，同时端射方向附近的阵增益要略高于正横方向附近的阵增益，此现象是由各向同性噪声的相关性结构以及有效的噪声功率随方位角的变化规律引起的，文献［9］中用CBF方法仿真得到了相同结论并给出了相关解释.随着阵列误差强度的增加，阵增益出现整体下降，均方差也相应升高.有趣的是，在阵元位置误差影响下，端射方向附近的阵增益变化得较明显，而在阵元姿态误差的影响下，正横方向附近的阵增益扰动幅度会较大;若要利用此阵列测量海底目标［13］(此时要求的仰角会比较大)，建议尽量控制阵元位置误差的大小以保证足够精度，例如为了保证70°方位上的阵增益损失不低于6.5 dB，就应使得σr＜0.05λ.表1的首列数据表示阵元间距，第2列数据表示各方向最优阵增益的均值，即.可看出，在各项同性噪声场中，阵增益会随阵元间距的增大而增加，当d＞0.5λ后基本趋于稳定.表中其他部分的数据等于E(GMVDR(θ))}，反映了不同阵列误差和输入信噪比ri变化时的阵增益损失量.可以看出，信噪比越大，阵增益对阵列误差越敏感，这与式(26)给出的结论吻合.同时随着阵元间距的增加，阵增益损失量会逐渐减小，当后基本趋于稳定.原因之一是当后几乎所有的相关系数受阵列误差的影响程度都被控制在一个很小范围内(见图3、4).声矢量阵具有“抗栅瓣模糊”的能力，因此在实际布放过程中，可以适当地增大阵元间距以提高阵列系统的鲁棒性，但是增大阵元间距也势必会使得阵列孔径过大，需在两者之间寻求折衷.

图6 各向同性噪声场中的阵增益Fig.6 Array gain in spherically-isotopic noise field

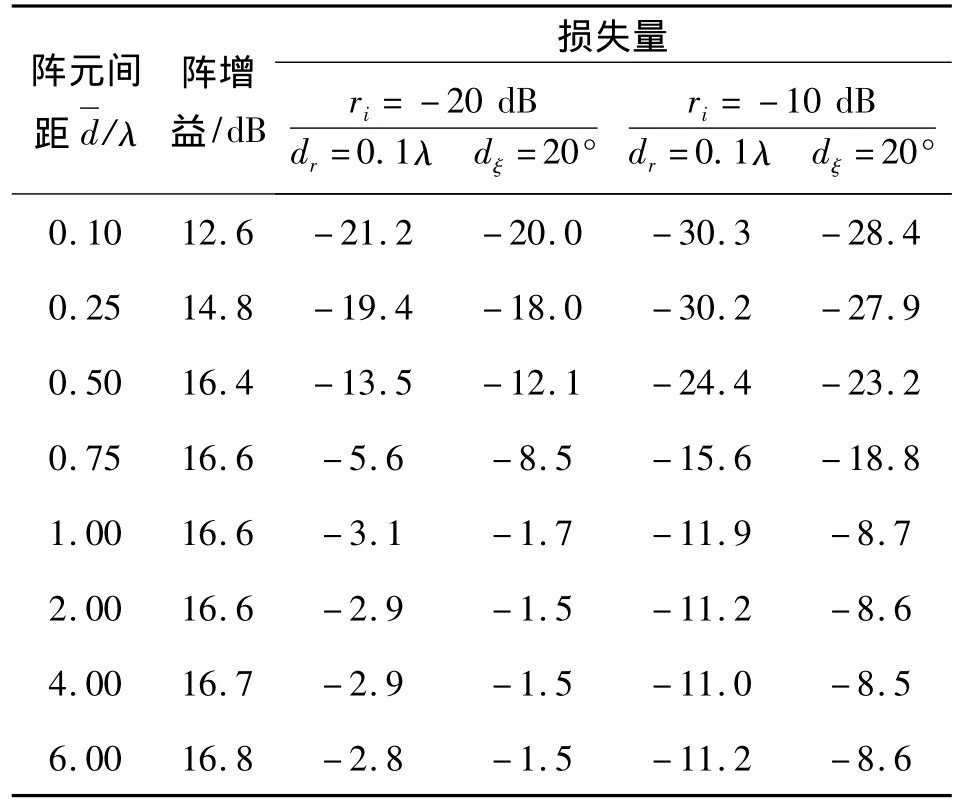
表1 阵增益损失量Table 1 Loss of the array gain

4 结论

针对处于方向性噪声场和各向同性噪声场中的声矢量阵，通过建立阵元位置误差和阵元姿态误差的高斯扰动模型，研究了随机阵列误差对噪声相关性结构和MVDR波束形成器阵增益的影响.研究结果表明:

1)阵列误差会改变相关系数的数值大小而不改变其奇偶虚实性，会导致原来不为0的相关系数出现波动和衰减，且程度与阵列误差的强度成正比;会使原来恒等于0的相关系数不再为0，而这些相关系数可能会成为造成系统不稳定的重要因素;

2)阵增益的损失由噪声相关性的破坏和导向矢量的失配引起，同时还受输入信噪比的影响.阵列误差的强度越大，导向矢量的失配程度越明显，阵增益就衰减得越严重;训练数据的输入信噪比越大，阵增益对阵列误差会越敏感;

3)相比于阵元姿态误差的影响，噪声的时空相关性和MVDR的阵增益都更易受到阵元位置误差的影响，因此有效的阵形估计方法变得很有意义.在各向同性噪声场中，阵增益对阵列误差的敏感度还与观察方向和阵元间距的大小有关.

文中的分析结果可为声矢量阵列系统的布放、相关算法的设计以及鲁棒性能的评估提供参考.

［1］SANTOS P，FELISBERTO P，JESUS S M.Vector sensor arrays in underwater acoustic applications［J］.IFIP Advances in Information and Communication Technology，2010，314:316-323.

［2］BENJAMIN M R.Autonomous control of an autonomous underwater vehicle towing a vector sensor array［C］//2007 IEEE International Conference on Robotics and Automation.Roma，Italy，2007，4562-4569.

［3］NEHORAI A，PALDI E.Acoustic vector-sensor array processing［J］.IEEE Transactions on signal processing，1994，42(9):2481-2491.

［4］HAWKES M，NEHORAI A.Acoustic vector-sensor beamforming and capon direction estimation［J］.IEEE Transactions on signal processing，1998，46(9):2291-2304.

［5］韩芳明，张守宏，潘复平.阵列误差对MUSIC算法性能的影响与校正［J］.西安电子科技大学学报，2003，30 (5):585-589.

HAN Fangming，ZHANG Shouhong，PAN Fuping.Effect of array uncertainty on the performance of MUSIC and its calibration［J］.Journal of Xidian University，2003，30(5): 585-589.

［6］杨晓冬，张灵珠.宽带数字波束测向系统性能分析［J］.哈尔滨工程大学学报，2009，30(10):1175-1179，1193.

YANG Xiaodong，ZHANG Lingzhu.Performance analysis of a wideband digital beamforming［J］.Journal of Harbin Engineering University，2009，30(10):1175-1179，1193.

［7］王晓晨，赵辉，马克茂.一种新型全姿态飞行仿真转台的运动学分析［J］.中国科学(信息科学)，2010，40 (4):549-560.

WANG Xiaochen，ZHAO HUI，MA Kemao.The kinematic analysis of a new all-attitude flight simulator turntable［J］.Scientia Sinica(Informationis)，2010，40(4):549-560.

［8］姚直象，胡金华，姚东明.基于多重信号分类法的一种声矢量阵方位估计算法［J］.声学学报，2008，33(4): 305-309.

YAO Zhixing，HU Jinhua，YAO Dongming.A bearing estimation algorithm using an acoustic vector sensor array based on MUSIC［J］.Acta Acustica，2008，33(4):305-309.

［9］HAWKES M，NEHORAI A.Acoustic vector-sensor correlations in ambient noise［J］.IEEE Journal of Oceanic Engineering，2001，26(3):337-347.

［10］孙贵青，杨德森，时胜国.基于矢量水听器的声压和质点振速的空间相关系数［J］.声学学报，2003，28(6): 509-513.

SUN Guiqing，YANG Desen，SHI Shengguo.Spatial correlation coefficients of acoustic pressure and particle velocity based on vector hydrophone［J］.Acta Acustica，2003，28(6):509-513.

［11］黄益旺，杨士峩，朴胜春.体积噪声矢量场空间相关特性研究的一种方法［J］.哈尔滨工程大学学报，2009，30(11):1209-1212.

HUANG Yiwang，YANF Shie，PIAO Shengchun.Research on spatial correlation in an acoustic vector noise field［J］.Journal of Harbin Engineering University，2009，30(11):1209-1212.

［12］王永良，丁前军，李荣锋.自适应阵列处理［M］.北京:清华大学出版社，2009:66-69.

［13］PENG H S，LI F H.Geoacoustic inversion based on a vector hydrophone array［J］.Chin Phys Lett，2007，24(7): 1977-1980.