ASUKF方法在航天器自主导航中的应用

李璟璟，张迎春，2，李化义，陈雪芹

(1.哈尔滨工业大学 卫星技术研究所，黑龙江 哈尔滨 150001;2.深圳航天东方红海特卫星有限公司，广东 深圳 518057)

在航天器自主导航技术中，系统的测量数据通常都会带有随机噪声误差，由于实际卫星导航系统大部分都是非线性系统，因此需要用非线性滤波方法得到系统状态变量的最优估计.EKF方法［1］虽然在工程中有广泛的应用，但是其对非线性方程的可微要求以及一阶近似的处理方法，限制了应用的范围和精度的提高.Julier等［2-3］提出的UKF方法，通过广义状态点对系统状态的概率分布进行近似，避免了雅可比矩阵的求取，提高了滤波精度.

然而，UKF对于系统先验噪声的分布有更为苛刻的要求.其良好的估计性能建立在精确已知系统先验噪声分布的基础之上［4］.但是，在轨航天器面临的实际空间环境是错综复杂的，在航天器运行的过程中，噪声统计特性往往会发生变化.另外，由于受到空间各种不确定因素的影响，测量系统往往也会受到不同程度干扰［5］.当存在如上所述的不确定噪声及干扰的作用时，UKF算法的估计性能会严重下降，甚至出现发散.因此，如何提高滤波器的自适应能力成为航天器自主导航需要解决的问题之一.

针对这个问题，SONG［6］等通过对噪声方差进行估计得到了自适应UKF算法并将其应用到移动机器人的状态及参数估计中.齐俊桐［7］等提出了基于MIT规则的自适应UKF方法并将其应用在旋翼飞行机器人的容错控制中.然而，这些方法都需要进行大量的偏微分计算，当系统维数较大时，必然会影响计算速度，增加计算机负荷.Kim［8］等通过自适应因子对EKF迭代过程中的方差阵和增益阵进行调整，得到自适应EKF算法并将其用在INS-GPS系统的状态估计中.该方法提高了EKF的自适应能力，但是仍然保持在一阶估计精度.裴福俊［9］等提出了基于神经网络辅助的自适应SSUKF方法并应用到车载组合导航系统的信息融合中.该方法与UKF相比具有较好的自适应能力和较短的计算时间，但由于神经网络需要一个预先训练的过程，这极大地影响了该方法在航天领域中的应用.

本文针对受到不确定因素影响的星敏/地平仪自主导航系统，在现有自适应估计方法的基础上，做了进一步的改进.通过对状态方程进行Unscented变换，对观测方程围绕状态估计点进行线性化，并引入自适应因子，在航天器自主导航系统中的仿真表明，ASUKF方法对不确定的噪声和干扰影响具有一定的自适应能力，并较AEUKF节约了计算时间.

1 ASUKF滤波方法

ASUKF滤波方法通过超球面分布变换以及自适应过程的实现在自适应调节的同时降低计算量.

1.1 Unscented变换

UT变换是UKF算法的核心，其基本原理是用采样点的分布来近似随机变量的概率分布，由被估计量的“先验”均值和方差，产生一批离散的与被估计量具有相同的概率统计特性的采样点，即Sigma点.它不必对状态方程和观测方程线性化，而是在状态矢量xk附近按一定规则选取有限的采样点，其均值和协方差分别为和，再根据生成的Sigma点，计算“后验”的均值和方差，将状态矢量的统计特性通过非线性系统传播.UT变换是UKF实现的基础，是其区别于其他非线性估计方法的本质特点.

对于状态变量xk，均值，方差，UT变换过程［10］为

将选取的状态矢量通过非线性函数f(·)，即χi，k/k－1=f(χi，k－1)，然后加权近似求解系统输出的统计特性:

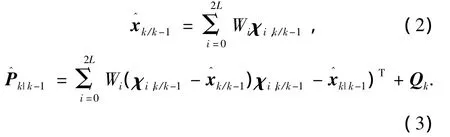
式中:

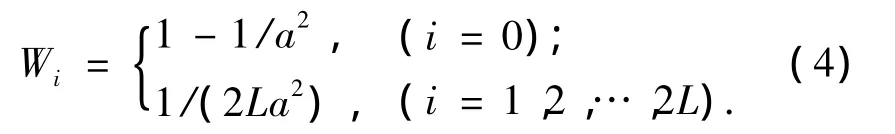
1.2 超球面分布变换(SSUT)

UKF方法通过UT变换得到了关于其均值对称分布的2n+1个采样点.在状态向量维数较高时，其计算效率较低.采用SSUT算法，可以在保证滤波精度的同时，将采样点个数由2n+1个缩减为n+2个，在一定程度上节约了计算时间，提高了计算效率［11-12］，降低了星载计算机的负荷［13］.

SSUT算法通过n+1个分布在以随机状态均值为原点的超球面上的相等权值的采样点来近似状态的概率分布.这样，由超球面分布采样点和状态均值点构成n+2个Unscented变换采样点.均值为0，均方差阵为单位阵的n维随机变量的超球面分布采样点算法如下［12］:

1)选择权值W0，满足0≤W0≤1.

2)确定权值Wi:

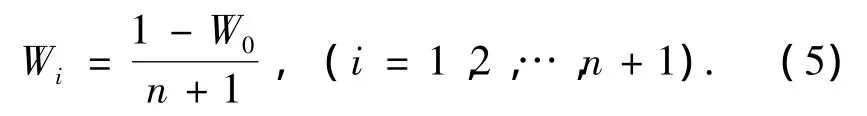
3)初始化向量序列:

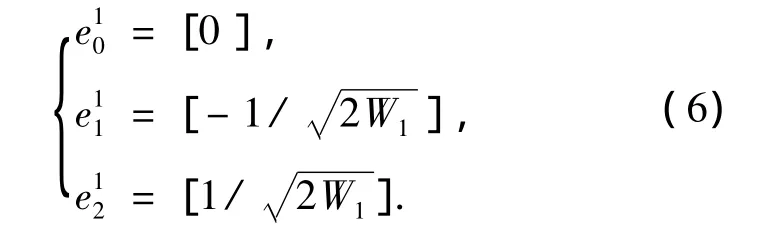
4)扩展向量序列.对于j=2，3，…，n，递推计算:

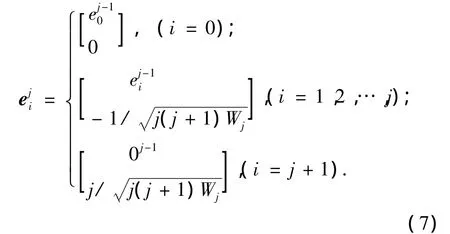
1.3 基于自适应因子的自适应方法

在EKF滤波过程中，系统新息为

引入对角矩阵βk=diag(β1，k，…，βn，k)输出预测误差相关函数形式［8］为

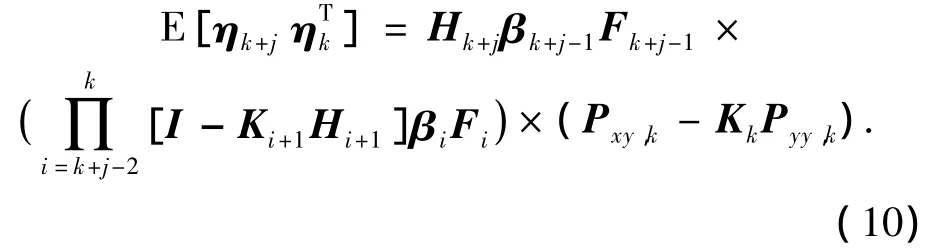
为使估计器能够准确的进行状态估计，需使输出预测误差序列{，…，}达到不相关零均值高斯序列.则根据方程，只需

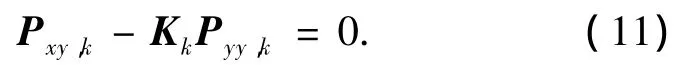
为使上式成立，可引入自适应因子αk［8］为

其中，新息方差阵:

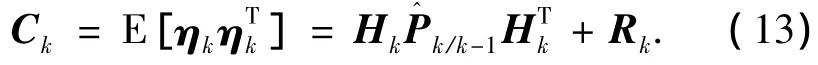
估计的新息方差阵:

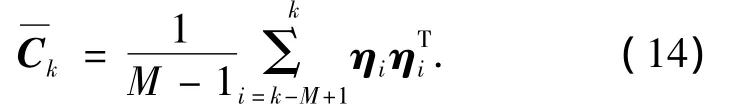
同时引入 λk≥1，对进行自适应校正，有=λkPk/k－1，其中，Pk/k－1为系统不完全方差阵.通过λk和αk修正可得新的先验状态估计误差方差矩阵为

在更新迭代过程中

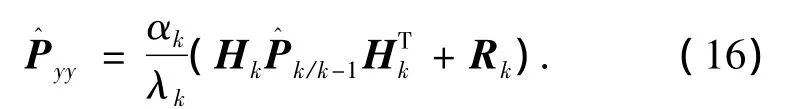
M为所选取的累加窗口.通过对M的选择，系统能够有效利用测量量的历史信息，从而对当前的迭代矩阵进行调整，实现对不确定噪声和干扰的自适应.当系统先验信息不精确时，λk和αk的取值一般可遵从如下规则:

2)调节增益阵Kk:取λk=1，此时自适应因子主要调节的是系统的增益矩阵，主要适用于观测方程存在不确定先验统计信息的情况.

1.4 ASUKF状态估计方法

当存在不确定性因素影响时，非线性系统可表示为

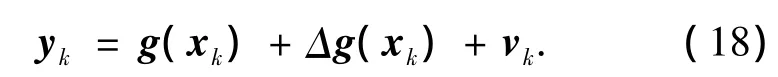
式中:Δf(xk)为不确定过程噪声方差阵、未知输入干扰或系统模型不确定性引起的系统状态方程不确定项，Δg(xk)为不确定测量噪声方差阵和未知输入干扰引起的系统测量方程不确定项，Δf(xk)、Δg(xk)与Qk、Rk以及xk相互独立.EKF方法将f(xk)、g(xk)分别围绕滤波值和估计值进行泰勒展开，并略去二阶以上项，在卡尔曼滤波框架下进行状态估计.其缺点是需要计算状态方程和观测方程的雅可比矩阵，计算量大，精度不够高.UKF方法通过Unscented变换，利用确定性采样形式，在避免了计算雅可比矩阵的同时，提高了估计精度.但是UKF的显著缺点是对系统先验信息的要求非常严格，当先验信息与实际不符时，容易导致UKF的发散.为了综合2种估计方法的优点，首先将状态方程进行Unscented变换处理，对观测方程求取雅可比矩阵，同时迭代估计过程中引入自适应调节因子，得到AEUKF方法，为了进一步降低计算时间，将状态方程用SSUT变换取代Unscented变换，最终得到ASUKF方法.该方法在降低算法复杂度的同时，减缓了由于先验信息不准确造成的估计发散问题.由于AEUKF与ASUKF的区别仅在于采样方法的不同，因而只给出ASUKF算法如下:

1)对于状态变量xk，均值，方差，进行SSUT变换:

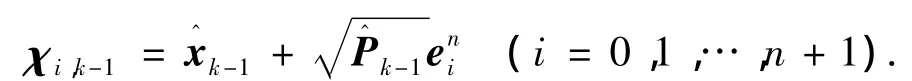
2)预测过程:

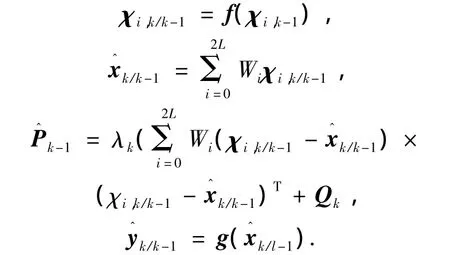
3)更新过程:

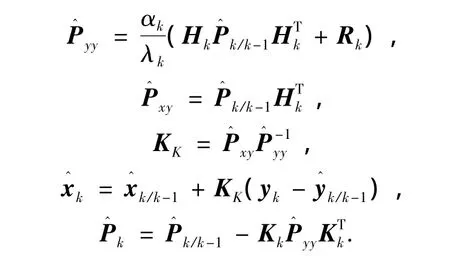
2 组合导航系统模型

在J2000.0地心赤道坐标系下，卫星自主导航系统建立为如下模型［14-16］:

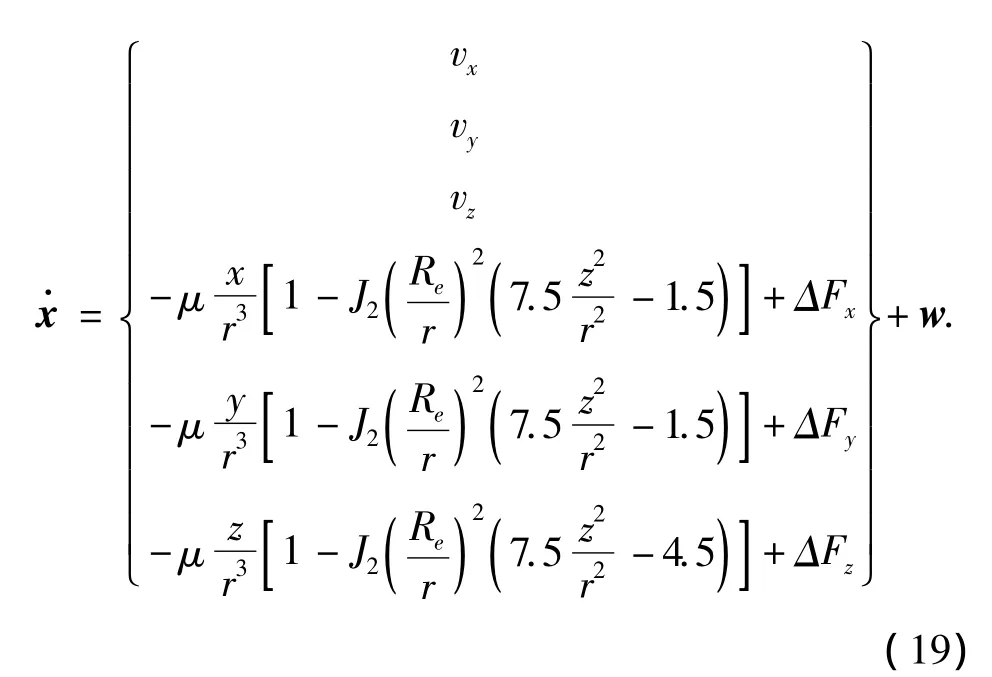
式中:x=［x y z vxvyvz］T，分别为卫星在3个坐标轴上的位置和速度，Re为地球半径，μ为地心引力常数，J2为地球引力二阶带谐项系数，ΔFx、ΔFy、ΔFz为地球非球形摄动的高阶摄动项和日、月摄动以及太阳光压摄动和大气摄动等其他摄动力影响.

采用直接敏感地平技术中的星光角距α作为观测量，可建立观测方程为

式中:r是航天器在地心惯性坐标系中的位置矢量，由地平敏感器获得，s是导航星星光方向的单位矢量，由星敏感器识别，ε为测量方程的残差.

当航天器在轨运行时，由于空间环境的复杂性，使实际的噪声统计特性往往产生变化，同时，各种空间干扰也会对测量方程的输出产生一定的影响.考虑测量方程在测量过程中噪声发生变化，同时受到不确定干扰的情况.对于不确定噪声，假设在某时间段噪声统计特性跳变为Δvk，Δvk～N(0，ΔRk)，对于不确定常值干扰Δb，假设可用如下方程描述:

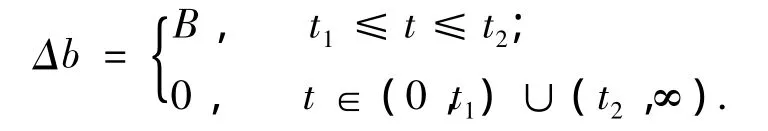
式中:B为干扰幅值.

3 ASUKF方法在天文导航系统中的仿真验证

对于方程(19)、(20)组成的天文导航系统，文献［15］利用UKF方法对系统进行导航参数估计，并通过仿真证明了UKF方法用于自主导航系统的有效性.在实际系统中，系统建模误差、先验噪声信息估计不足以及空间环境干扰都可引起方程(18)中Δ项的变化.单纯采用UKF方法很容易使估计过程出现较大的偏差.而采用ASUKF方法，可以使滤波器对系统的不确定性具有一定的自适应能力.分别在理想情况下和存在不确定性影响的情况下进行仿真.系统在理想情况下的仿真，是为了验证ASUKF方法的精度;在不确定环境影响下的仿真，可以验证自适应方法的有效性.

选取仿真场景［16］为:半长轴a=7 136.635，偏心率e=0.001 809轨道倾角i=65°，升交点赤经Ω=30°，近地点角距ω=30°，星敏感器的视场为20°×20°，星敏感器精度3″，红外地平仪精度为0.02°，导航星选用均匀分布在天球上的40颗星.假设系统的测量噪声方差阵为:Rk=4×10－6，仿真中取M=20.

分别采用UKF、AEUKF和ASUKF滤波算法进行自主导航解算，图1和图2分别给出了3个轴的位置和速度的估计误差仿真结果.由图可见，3种滤波方法的估计误差都能够较好地趋于收敛.

图1 位置估计误差Fig.1 Estimate error of position

图2 速度估计误差Fig.2 Estimate error of velocity

为了进一步比较估计效果，分别对3种方法进行100次Monte Carlo仿真，将滤波稳定后的数据求取均方根误差均值，同时求取滤波过程所用的时间平均值.结果如表1所示，可见3种方法精度的数量级相同.数值上UKF精度略高，这是因为AEUKF和ASUKF方法观测方程采用了雅可比矩阵而不是采用UT变换.同样由于观测方程采用了雅可比矩阵并且ASUKF采用了SSUT变换，ASUKF的计算时间最少.这表明了ASUKF方法的有效性.自适应因子变化过程如图3所示.通过图3可以看到，在噪声统计特性准确及没有干扰的情况下，AEUKF和ASUKF方法的自适应因子幅值变化比较平缓.

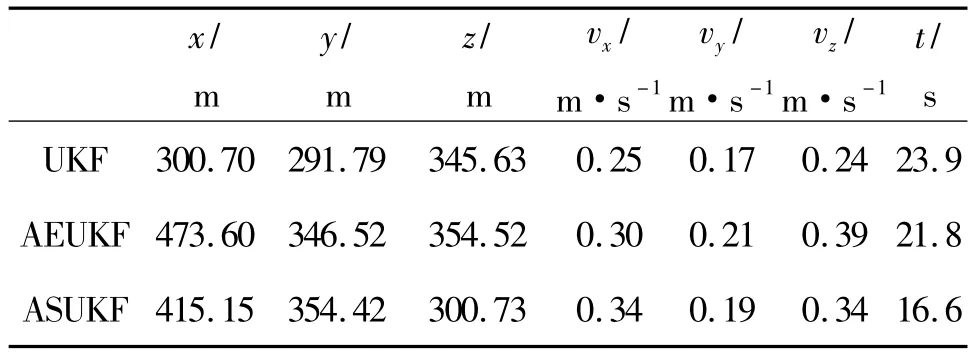
表1 均方根误差Table 1 RMS error

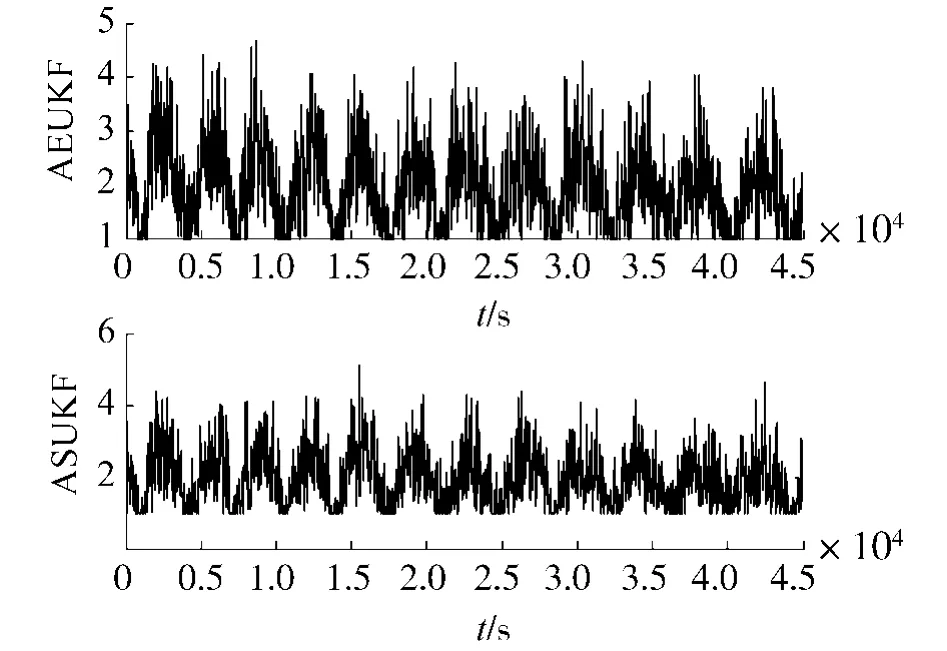
图3 自适应因子Fig.3 Adaptive factor

在实际的空间环境中，航天器面临的噪声特性和干扰幅值往往是不确定的范围，为验证ASUKF方法的自适应能力，假设在系统估计过程的第1 500 s～2 000 s，系统观测噪声扩大为原来的100倍，同时常值干扰幅值为0.05，干扰作用时间为3 s.分别采用3种方法对航天器的位置和速度进行估计，估计误差分别如图4和图5所示.由图可见，在受干扰的时间段内，UKF滤波方法的估计误差变化较为剧烈，而AEUKF和ASUKF由于自适应因子的调节作用，基本不受未知噪声和扰动的影响.

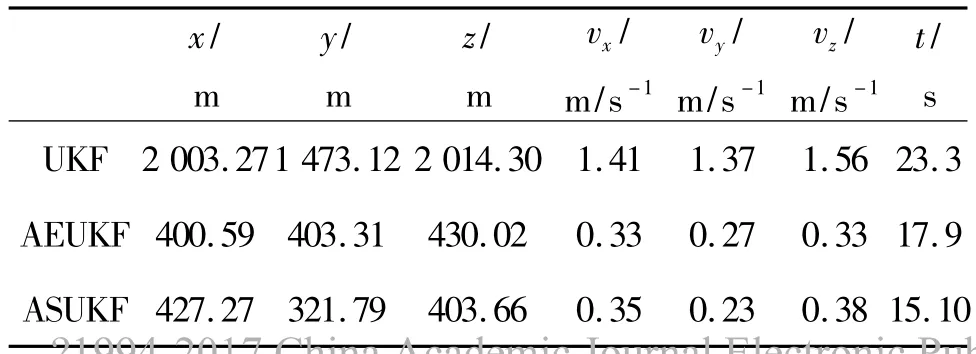
表2 均方根误差Table 2 RMS Error

图4 位置估计误差Fig.4 Estimate error of position

图5 速度估计误差Fig.5 Estimate error of velocity

图6 自适应因子Fig.6 Adaptive factor

表2给出了存在如上所述的噪声和干扰时，分别进行100次Monte Carlo仿真所得到的均方根误差均值以及滤波过程所用的平均时间.

通过以上仿真可以看出，当系统噪声统计特性发生变化，同时存在常值干扰时，用UKF方法进行的位置和速度估计，显然受到较大的影响，在受到干扰的时间段内，估计精度较差.而AEUKF和ASUKF方法基本不受未知噪声和扰动的影响，能够快速达到稳定，显示出良好的自适应能力.自适应因子变化情况如图6所示，由图可见，随着噪声和干扰的变化，两者自适应因子也较快地做了相应的调整，以使估计过程适应误差阵及观测量的变化.从滤波时间上看，不论是否存在未知噪声及干扰，ASUKF方法的计算时间最短，这对于提高星载计算机计算效率具有一定的意义.

4 结束语

本文以自主导航系统为背景，提出了一种具有一定自适应能力的状态估计算法-ASUKF算法.该算法结合EKF和UKF方法的优点，对系统状态方程进行SSUT变换，对系统测量方程求取雅可比矩阵.考虑到系统测量过程中噪声和干扰的不确定性，在迭代过程中引入了自适应因子，利用测量量的历史数据对方差阵或增益阵进行实时调整，使滤波器具有了自适应能力.与传统的UKF方法以及仅具有自适应调节因子的AEUKF方法相比，ASUKF方法明显提高了计算效率，对不确定的噪声和干扰具有较强的自适应能力.这对航天器高精度自主导航的工程实现具有一定的参考价值.

［1］LERRO D，BAR-SHAOM Y K.Tracking with debiased consistent converted measurements vs.EKF［J］.IEEE Transaction on Aerospace and Electron System，1993，29: 1015-1022.

［2］JULIER S J，UHLMANN J K.Unscented filtering and nonlinear estimation［J］.Proceedings of IEEE，2004，92(3): 401-422.

［3］潘泉，杨峰，叶亮.一类非线性滤波器——UKF综述［J］.控制与决策，2005，20(5):481-494.

PAN Quan，YANG Feng，YE Liang.Survey of a kind of nonlinear filters—UKF［J］.Control and Decision，2005，20(5):481-494.

［4］ZHAO Lin，WANG Xiaoxu.An adaptive UKF with noise Statistic Estimator［C］//4th IEEE Conference on Industrial Electronics and Applications，ICIEA 2009.Xi＇an，China，2009:614-618.

［5］高为广，何海波，陈金平.自适应UKF算法及其在GPS/ INS组合导航中的应用［J］.北京理工大学学报，2008，28(6):505-509.

GAO Weiguang，HE Haibo，CHEN Jinping.An adaptive UKF algorithm and its application for GPS/INS integrated navigation system［J］.Transactions of Beijing Institute of Technology，2008，28(6):505-509.

［6］SONG Qi，HAN Jianda.An adaptive UKF algorithm for the state and parameter estimations of a mobile robot［J］.Acta Automatica Sinica，2008，34(1):72-79.

［7］齐俊桐，韩建达.基于MIT规则的自适应Unscented卡尔曼滤波及其在旋翼飞行机器人容错控制的应用［J］.机械工程学报，2009，45(4):115-124.

QI Juntong，HAN Jianda.Adaptive UKF and its application in fault tolerant control of rotorcraft unmanned aerial vehicle［J］.Journal of Mechanical Engineering，2009，45(4): 115-124.

［8］KIM K H.The stability analysis of the adaptive fading extended Kalman filter using the innovation covariance［J］.International Journal of Control，Automation，and Systems，2009，7(1):49-56.

［9］裴福俊，居鹤华，崔平远.基于自适应SSUKF的组合导航信息融合方法［J］.系统工程与电子技术，2009，31 (5):1217-1221.

PEI Fujun，JU Hehua，CUI Pingyuan.Information fusion method based on adaptive SSUKF for integrated navigation system［J］.Systems Engineering and Electronics，2009，31 (5):1217-1221.

［10］JULIER S J.The scaled unscented transformation［C］// Proceedings of the American Control Conference.Anchorage，AK，2002.

［11］JULIER S J，UHLMANN J K.Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations［C］//Proceedings of the American Control Conference.Anchorage，AK，2002.

［12］JULIER S J.The spherical simplex unscented transformation［C］//Proceedings of the American Control Conference.Denver，Colorado，2003.

［13］郭云飞，吴庆宪，姜长生.基于修正罗德里格参数的小卫星SSUKF姿态确定［J］.上海航天，2008(6):12-25.

GUO Yunfei，WU Qingxian，JIANG Changsheng.Attitude estimation using modified rodrigues parameters based on SSUKF for micro-satellite［J］.Aerospace Shanghai，2008(6):12-25.

［14］刘林.航天器轨道理论［M］.北京:国防工业出版社，2000: 20-50.

［15］XIONG K，LIU L D，ZHANG H Y.Modified unscented Kalman filtering and its application in autonomous satellite navigation［J］.Aerospace Science and Technology，2009，13:238-246.

［16］张共愿，程咏梅，杨峰.预测—校正EKF算法在自主导航中的应用［J］.宇航学报，2009，30(6):2227-2230.

ZHANG Gongyuan，CHENG Yongmei，YANG Feng.Applying of Forecast-revise EKF algorithm in autonomous navigation system［J］.Journal of Astronautics，2009，30(6): 2227-2230.