喷动床DEM模拟曳力模型评价

朱卫兵，朱润孺，邢力超，孙巧群

(哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001)

喷动床最早由加拿大的Mathur和Gishler发明，最初用于谷物干燥，如今喷动床已经被广泛的应用到干燥、造粒、粉碎、煤燃烧和气化、铁矿石还原、油页岩热解、焦炭活化、石油热裂化等领域［1］.在典型的喷动床型中，矩形喷动床与柱锥型喷动床相比，不但具有较低的最小喷动速度和最大喷动压降的优点，还具有气固接触效率好、传热效率高的优点，且几何结构简单，易于制造.

颗粒在喷动床内运动，受到流体曳力、自身重力和颗粒间接触力等作用力，其中流体曳力是对喷动床进行数值研究时，唯一的相间相互作用力，因此曳力模型的选择是数值结果精确与否的关键.Du Wei［2］等人采用双流体模型(two fluid model，TFM)对柱锥型喷动床的曳力模型选择进行了研究，Li Jie＆Kuipers J A M［3］对Hill等模型在流化床离散元法(discrete element method，DEM)模拟中的应用做了比较，而对于矩形喷动床相同问题的研究还未见报道，由此可见对矩形喷动床内颗粒运动现象的研究远不如柱锥床深入.喷动床DEM模拟中，Tsuji［4］模型和Ergun(ε＞0.8)+Wen－Yu(ε＜0.8)联合模型［5］是应用最广泛的曳力模型，而其他曳力模型，如Arastoopour［6］，Di Felice［7］和Syamlal＆O＇Brien［8］等模型还未见有研究报道采用.喷动床中，滚动的颗粒会受到滚动摩擦的作用，但在以往的喷动床DEM模拟中，滚动摩擦很少被考虑，只考虑滑动摩擦对颗粒运动的影响，这显然会使模拟与真实物理现象间存在差异.

针对喷动床DEM模拟中的曳力模型选择问题，以DEM数值模拟为手段，首次将Arastoopour、Di Felice、Syamlal＆O＇Brien曳力模型和Beer＆Johnson［9］滚动摩阻力矩表达式应用到矩形喷动床DEM(pseudo－three－dimensional)［10］模拟中，对矩形喷动床内颗粒运动进行研究，并将模拟结果与赵香龙［11］等人的实验结果比较，具体分析了不同曳力模型下的床内流动结构和空隙率、颗粒速度、力矩分布，以期为矩形喷动床数值研究中曳力模型的选择提供有益参考.

1 数学模型

CFD－DEM模型中，气相场采用欧拉法，固相场采用拉格朗日法.对于相间耦合，文中分别选择了Arastoopour、Di Felice、Syamlal＆O＇Brien和Tsuji等曳力模型.

1.1 气相模型

对于气相场采用标准k－ε模型，考虑气体的湍流运动.连续性方程和动量方程如下:

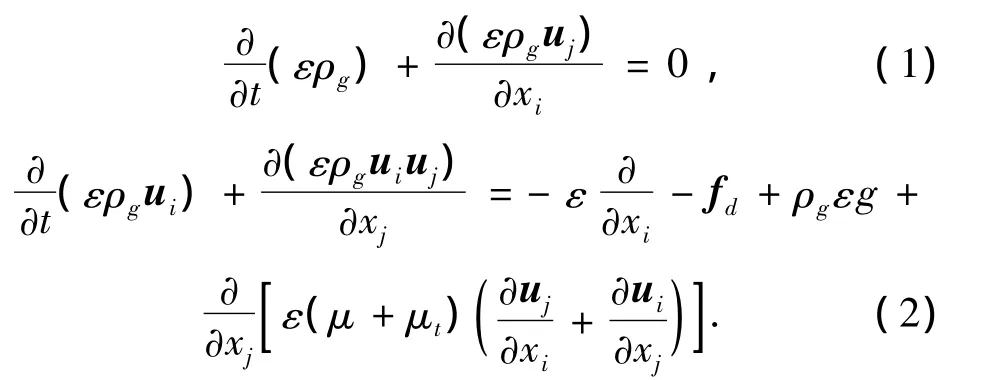
式中:ε、u、p、ρg和μ分别为孔隙率、气相速度、压力、密度和粘性.fd=β(u－v)，曳力系数β由式(11)～(14)确定.

湍流动能和湍流动量耗散方程如下:

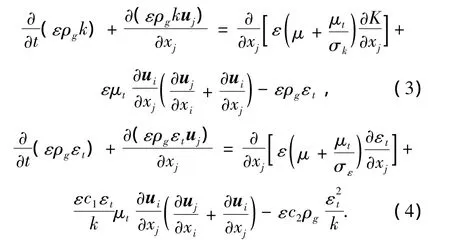
式中:k、εt分别为湍流动能和湍流动量耗散率.μt=cμρgk2/εt.方程中 c1、c2、cμ、σε和 σk的值见表1.

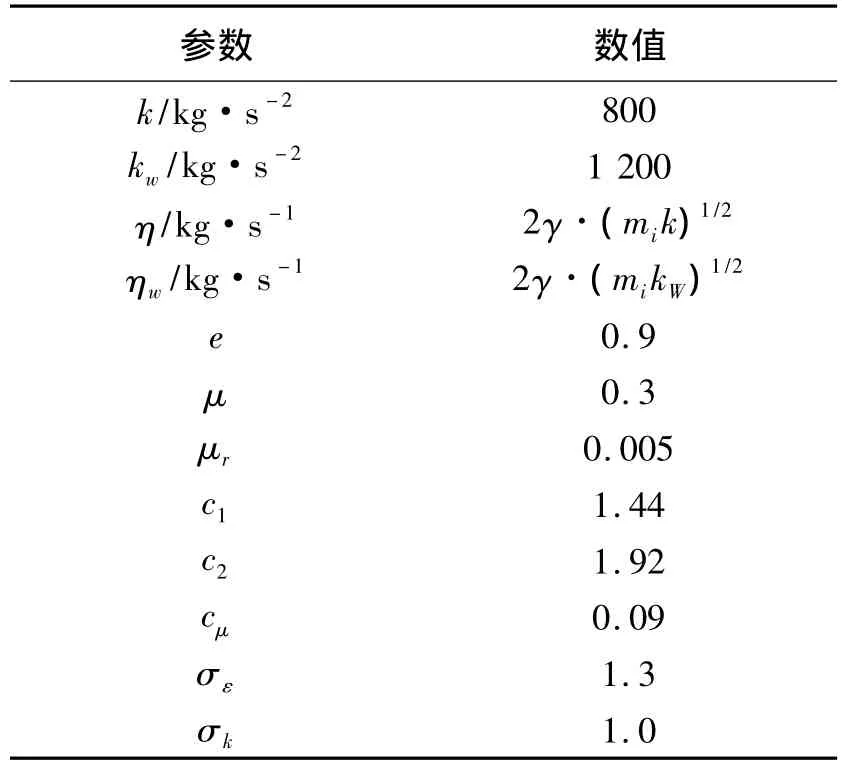
表1 模拟参数Table 1 Parameters for particle and fluid simulations

1.2 颗粒运动模型

颗粒的运动遵循牛顿第二定律，考虑重力、接触力、流体曳力和压力梯度力的作用.平动和转动运动方程为

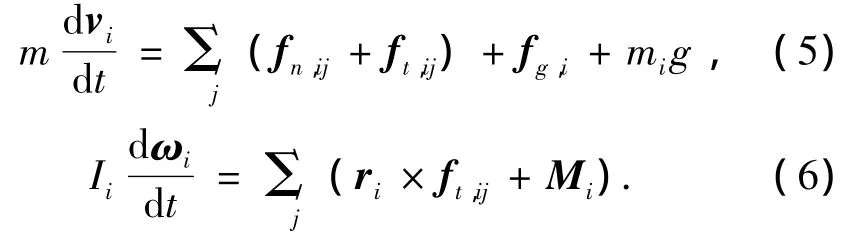
式中:

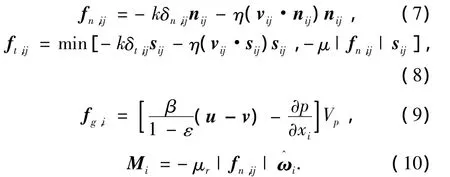
式中:dp、e、g、I、k、mi、Mi、nij、v、sij、δn，ij、δt，ij、μ、μr、η和ωi分别为颗粒直径、颗粒恢复系数、重力加速度、转动惯量、弹性系数、单个颗粒小球质量、滚动摩擦力矩、颗粒小球i和j之间的法向单位矢量、颗粒小球速度、颗粒小球i和j之间的切向单位矢量、颗粒小球i和j之间的法向变形、颗粒小球i和j之间的切向变形、滑动摩擦系数、滚动摩擦系数、阻尼系数和颗粒小球角速度.μ和μr的值见表1.

1.3 曳力模型

Arastoopour模型:

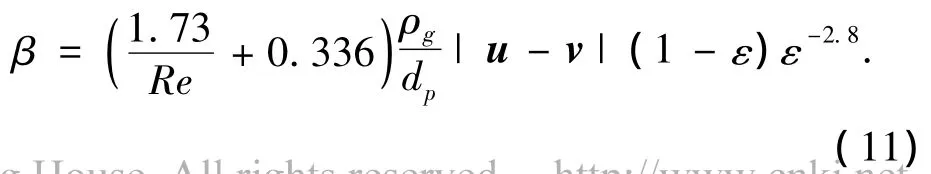
Di Felice模型:

式中:X=3.7－0.65exp［－0.5(1.5－lg Re)2］，

Syamlal＆O＇Brien模型:

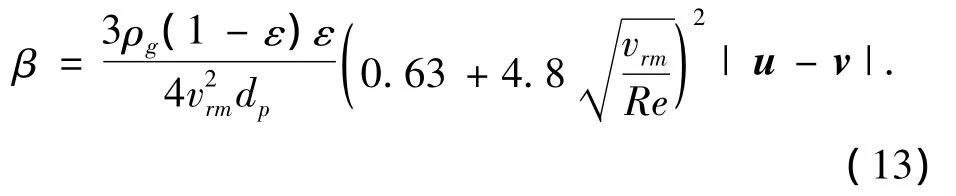
式中:vrm=0.5{A－0.06Re+［(0.06Re)2+;式(11)～(13)中，Re= (dp|u－v|ρg)/μ.

Tsuji模型:

1.4 模型及求解

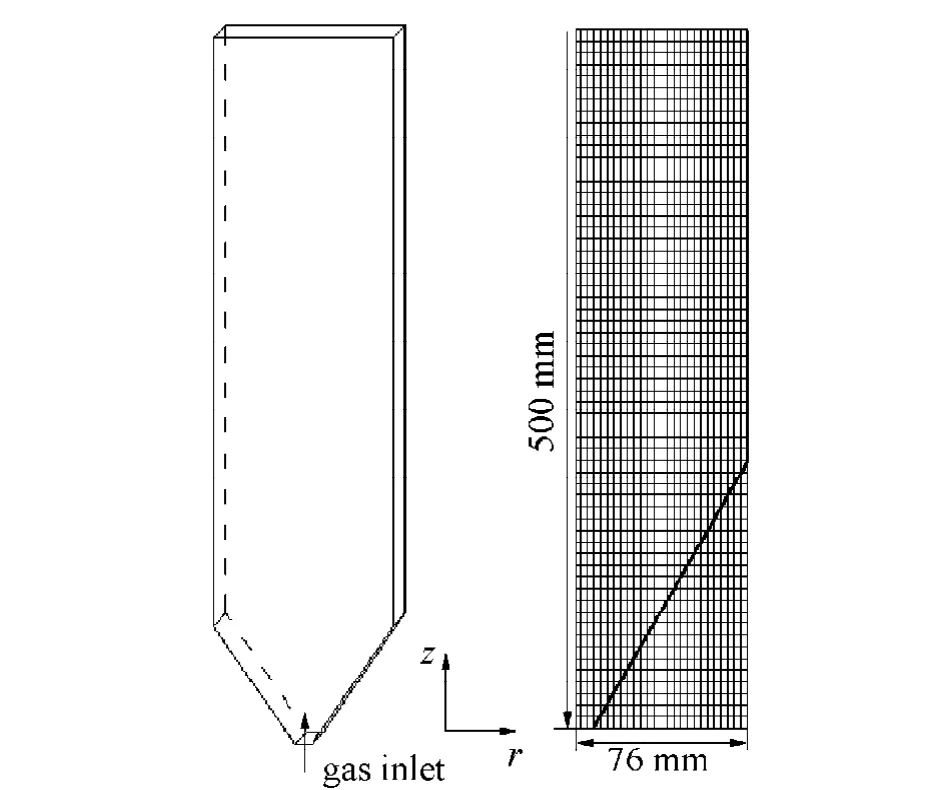
图1 几何模型Fig.1 Geometry of a vessel

模拟的对象为矩形喷动床，床体尺寸见图1，其中床厚15 mm，喷口宽9 mm.模拟所用网格尺寸为3 mm×2 mm×5.2 mm.计算颗粒直径2 mm，颗粒密度2 380 kg/m3，颗粒填充高度100 mm，气相参数选择空气在20℃，1.01×105Pa时的参数，表观气速Ug=1.58 m/s，固相颗粒计算时间步长为10－6s.采用交错网格技术，参照SIMPLE算法，对气相场和固相场连续交替耦合求解.对于模拟时最小喷动气速的确定，采用逐渐降低表观气速的方法.表观气速由1.6 m/s降到0.8 m/s后发现，4种模型的最小喷动速度均小于模拟工况.

2 结果与讨论

2.1 曳力系数分析

图2为不同曳力模型曳力系数随空隙率变化曲线，气固两相滑移速度选择15m/s.由图可见:1)空隙率大于0.8区域，不同曳力模型计算出的曳力系数值差异较小;2)空隙率在0.66～0.77内Tsuji模型曳力系数最大;3)空隙率大于0.47区域，Arastoopour、Syamlal＆O＇Brien模型分别和Tsuji模型有2个交汇点，在交汇点区间内，Arastoopour、Syamlal＆O＇Brien模型曳力系数均小于Tsuji模型曳力系数; 4)空隙率小于0.8区域，Di Flice模型曳力系数随着空隙率的减小而迅速增加，Arastoopour模型也显现出类似的趋势，但在数值上较小;5)空隙率小于0.47区域，Tsuji模型曳力系数最小.由以上分析可知空隙率变化造成了不同模型曳力系数的差异，而气固曳力是喷动床DEM模拟相间耦合的唯一作用力，并且喷动床内空隙率在不同区域相差较大，所以选择不同的曳力模型必将造成模拟的结果不同.

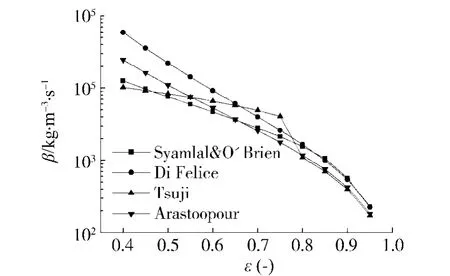
图2 曳力系数比较Fig.2 Comparison of drag force coefficients

2.2 流动结构

图3为不同曳力模型在1 s时颗粒分布的模拟结果，由图可以看出在同一时刻不同模型喷泉高度由高到低排列为:Di Felice、Arastoopour、Tsuji和Syamlal＆O＇Brien模型，Di Felice模型的喷射区直径最大，相应环隙区范围要小于其他3个模型，这是由于其在空隙率小于0.55区域曳力系数较大所致.

图4是不同曳力模型下的流动结构模拟结果，由图可以看出 Arastoopour、Syamlal＆O＇Brien和Tsuji模型的模拟结果均呈现出一种周期性喷动现象，周期大约为0.16 s，并且可以看出颗粒在喷泉区的运动呈现出均匀且对称性较好的颗粒群运动状态，这两点与图5的实验结果符合很好，而Di Felice模型的模拟结果没有出现这2种现象，所以不再对其进行进一步的讨论.

图3 不同曳力模型1 s时的流动结构Fig.3 The instantaneous flow patterns of different drag models at 1.0 s

图4 流动结构模拟结果Fig.4 Simulated result of flow patterns

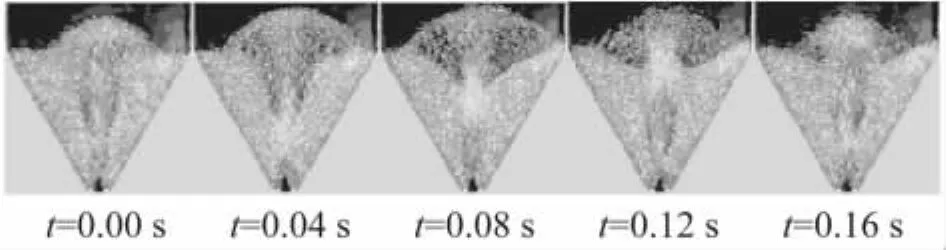
图5 流动结构实验结果Fig.5 Experimental result of flow patterns

2.3 空隙率分布

图6给出了不同床层高度下沿径向的空隙率分布.

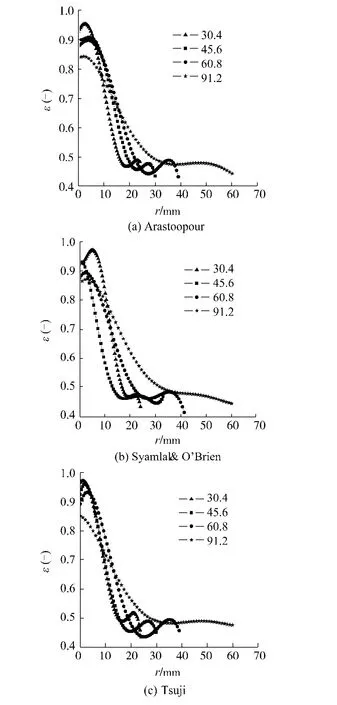
图6 空隙率分布Fig.6 Voidage profiles

由图可知3个模型的模拟结果均有以下现象: 1)随着床层高度的增加，喷射区的空隙率逐渐降低，且最小空隙率出现点外移，这与 Lim＆Mathur［12］给出的式(16)预测趋势相符;2)沿床体径向，空隙率成下降趋势，在喷射区和环隙区交界处呈现出很大的梯度，而在环隙区内变化较平缓.这2种现象和He［13－14］等人实验观察得到的结论相同.

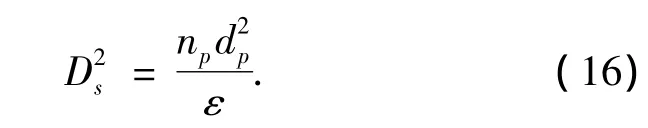
式中:Ds和np为喷射区直径和喷射区给定床高处颗粒数目.

2.4 轴线上的颗粒速度

图7(a)为颗粒轴向速度分布，实验结果表明沿轴线颗粒轴向速度由3个区组成:1)加速区，2)平缓区，3)减速区.这种现象有别于以往的实验结果［13－15］.采用标准k－ε模型和Beer＆Johnson表达式加入湍流和滚动摩擦2种因素的影响，区别于文献［11］采用Jones＆Launder低雷诺数k－ε模型和Brilliantov＆Poeschel滚动摩阻力矩表达式，由图可见2种方法均能很好地预测这种分布.

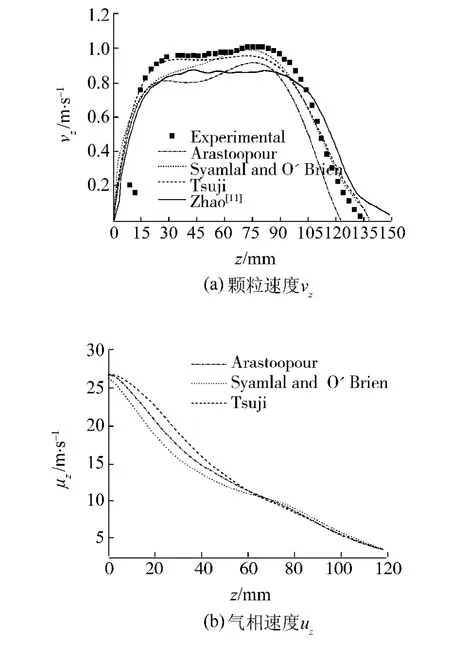
图7 轴线上轴向速度分布Fig.7 Velocities along spout axis

由图还可看出，在(1)区的低位3个模型和文献［11］的模拟结果相同，而到了高位Tsuji模型模拟结果与实验值符合更好;在(2)区Tsuji模型预测值整体与实验值最为接近，且好于文献［11］的模拟结果，Syamlal＆O＇Brien模型对最大值的预测最好;在(3)区，3个模型给出的变化趋势和实验值相符，数值上Arastoopour模型与实验值相差较大.图7 (b)给出的是气相轴向速度分布，由图可以看出:z＜60 mm区域，Tsuji模型预测的速度最大;60 mm＜ z＜90 mm区域，Syamlal＆O＇Brien模型预测值最大;而z＞90 mm区域，3个模型预测值几乎相同.3种模型预测的气相速度不同是造成3个模型预测颗粒速度差异的主要原因，因为气相作用力是喷射区的最大加速力，气相速度越大颗粒获的加速力就越大，从而得到较大的速度.

2.5 喷射区颗粒速度

图8为喷射区不同床高处的颗粒轴向速度分布.

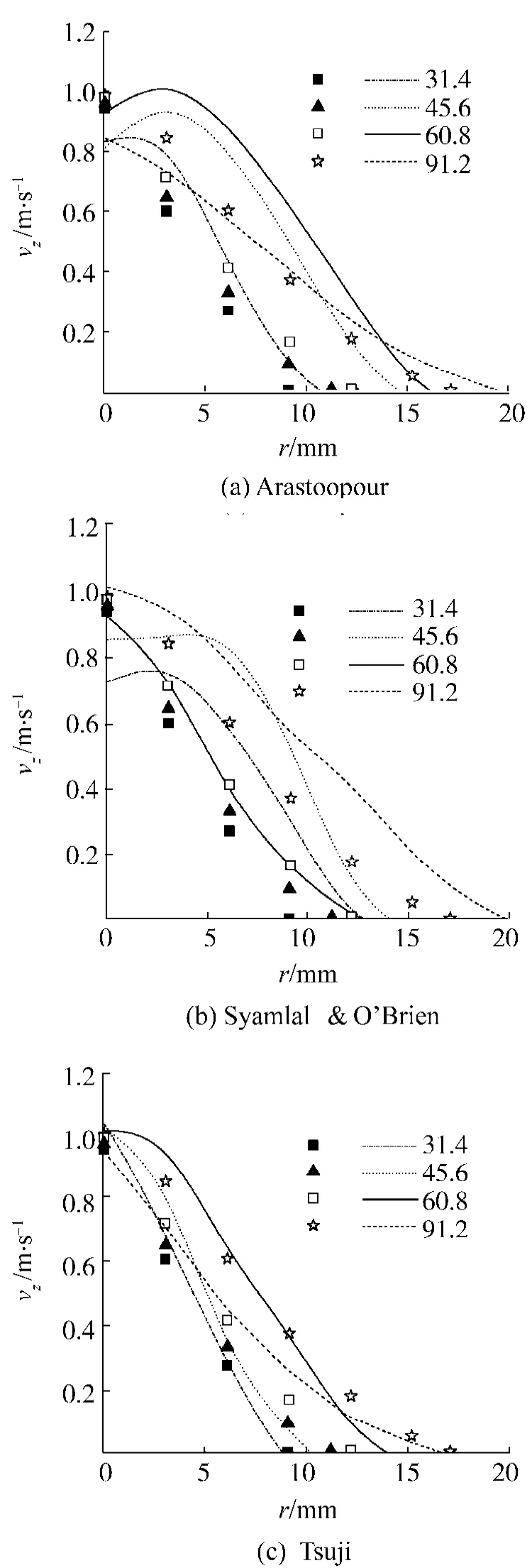
图8 喷射区颗粒速度分布Fig.8 Particle velocities in spout

由图可见实验结果呈现出类似立方函数的分布，vz随床层高度的增加而增大，Tsuji模型的模拟结果和实验结果趋势上符合较好，而其他2个曳力模型均有类似于San Jose［16］和赵香龙［17］提到的抛物线形式分布.由图还可看出31.4 mm和45.6 mm两个床层上Tusji模型结果与实验值符合的最好，60.8 mm床层上Syamlal＆O＇Brien模型结果与实验值符合最好，而在91.2 mm床层上模拟值均与实验结果存在较大差异.

2.6 环隙区内颗粒速度

图9为环隙区颗粒轴向速度分布，取竖直向下为正方向.由图可见模拟与实验结果均显示，在喷射区与环隙区交界处vz开始迅速增大，达到最大值后随r的增大而减小.图10为环隙区速度矢量分布，由图9、10可见径向上颗粒速度呈现出加速和减速两个区域，出现这种两区分布的原因是:在环隙区内颗粒受到的主要作用力为接触力，张勇等人［18］的研究结果表明颗粒碰撞频率在环隙区存在一峰值，与图9的颗粒速度分布相同，颗粒碰撞频率反应了颗粒间接触次数的多少，接触次数多，则颗粒所受接触力可能就大，从而使其速度增大，反之亦然，由此可知颗粒碰撞频率增加导致了vz增大.

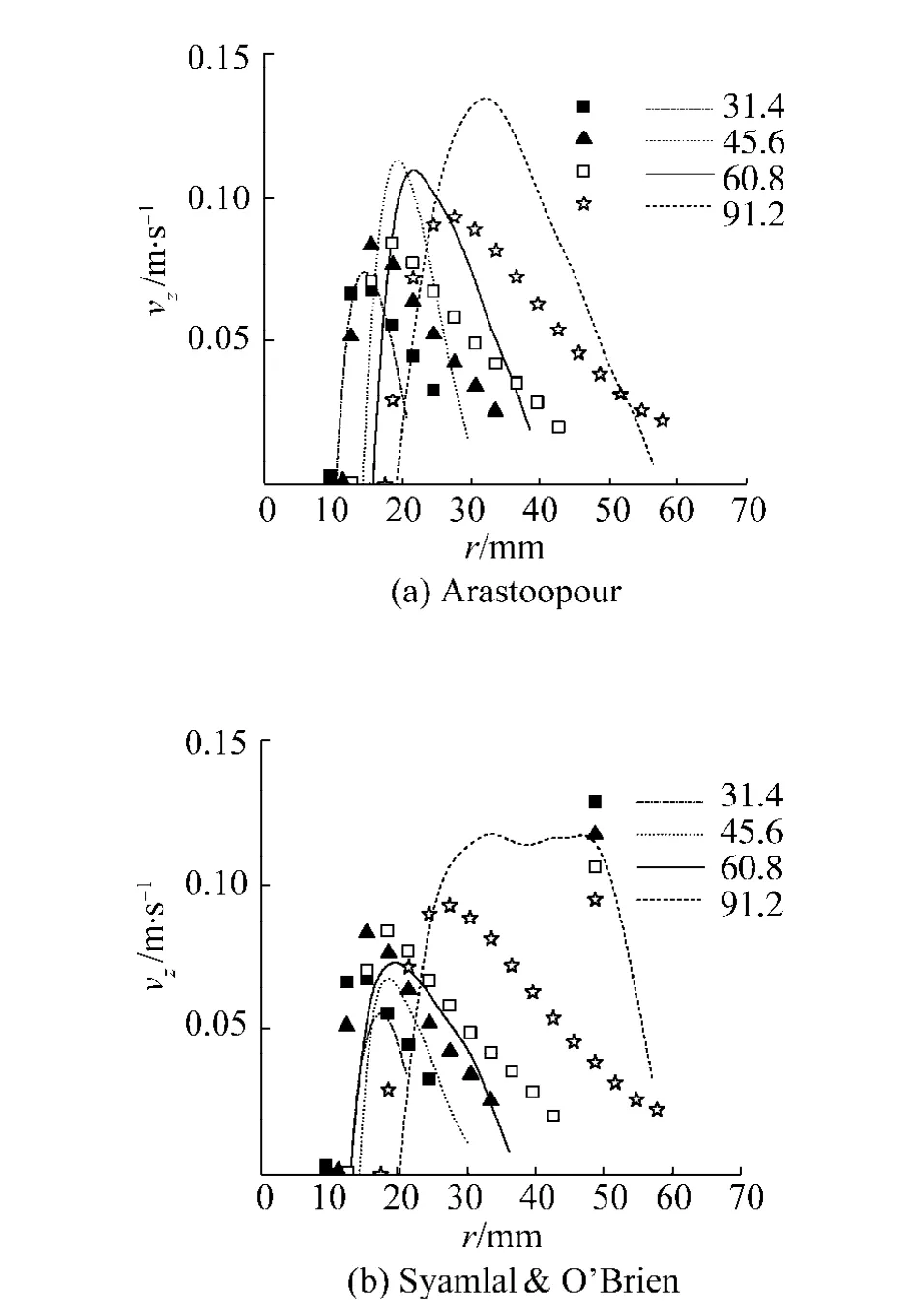
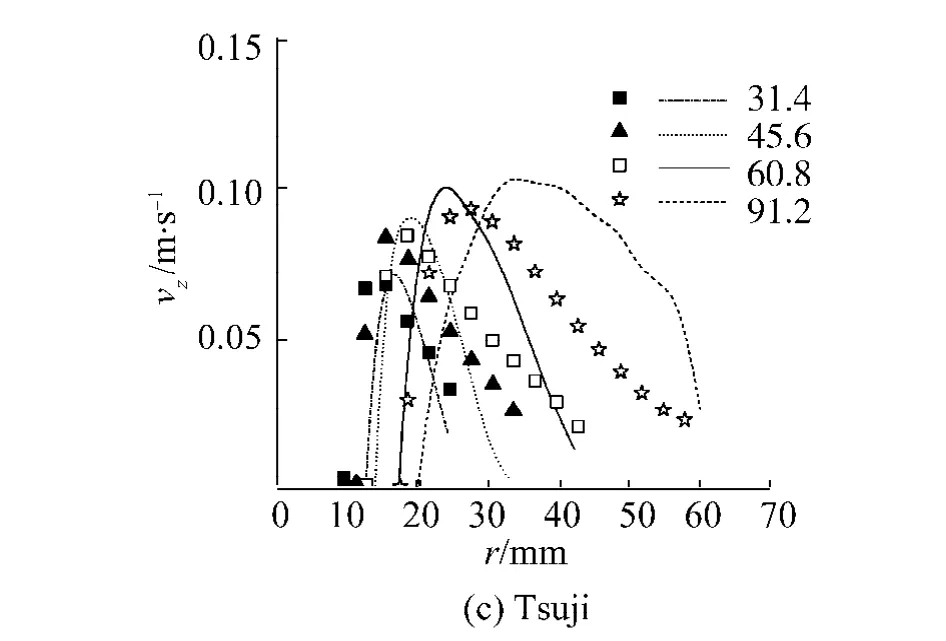
图9 环隙区颗粒速度分布Fig.9 Particle velocities in annulus

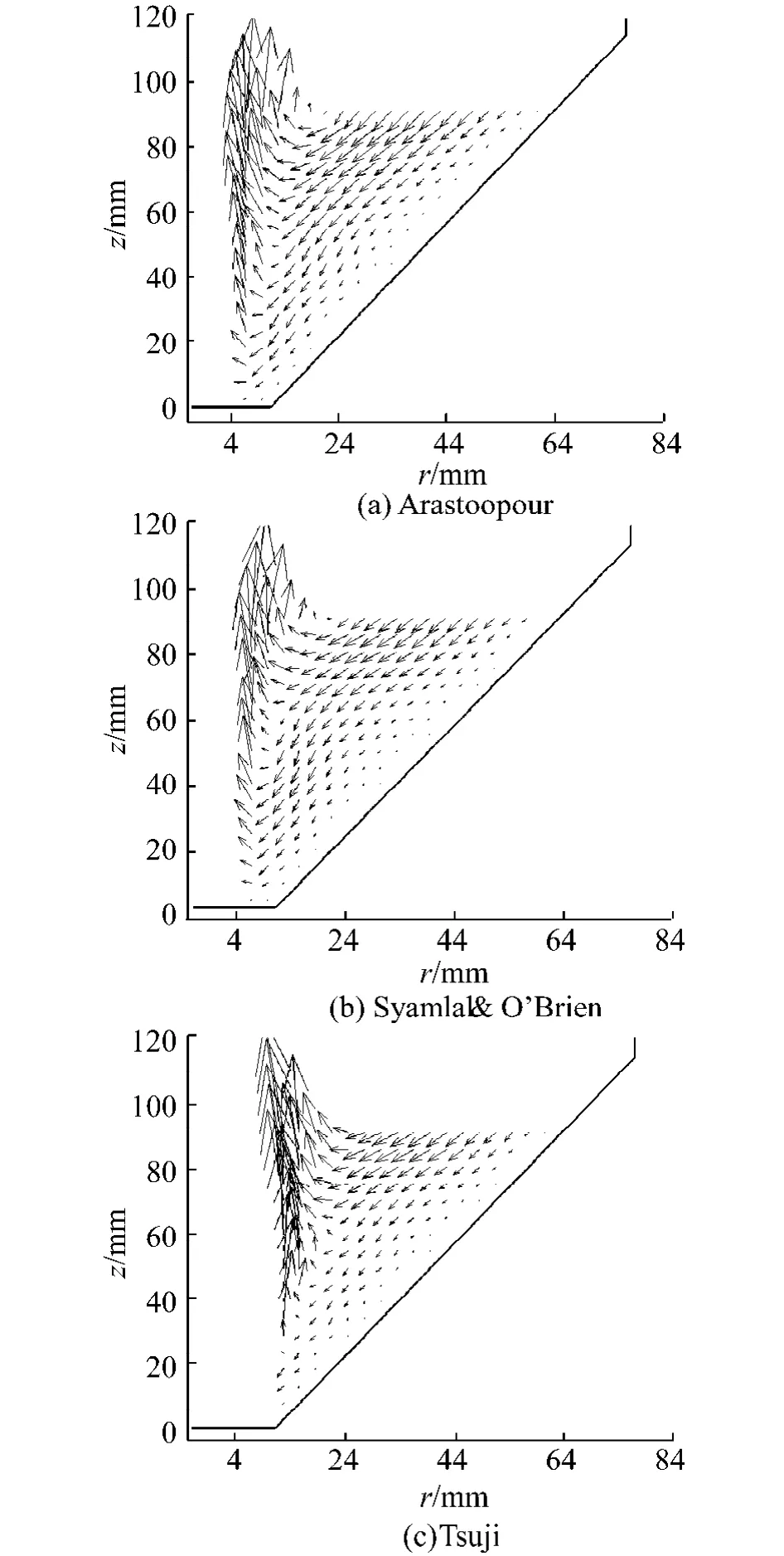
图10 喷动床局部颗粒矢量分布Fig.10 Vector fields of particle velocity in the local area of spouted bed

对于vz最大值的预测，Arastoopour模型的预测值与实验值相差最大，由91.2 mm至30.4 mm床高分别为实验值的1.47倍、1.4倍、1.36倍和1.15倍，与实验值符合最好的是Tsuji模型分别为1.12倍、1.14倍、1.12倍和1.14倍.虽然对于vz最大值的预测存在误差，但3个模型的模拟结果均好于TFM［2］和无滚动摩擦DEM［19］模拟结果的10倍和5倍误差，这说明滚动摩阻力矩的加入使速度最大值的预测更加精确.

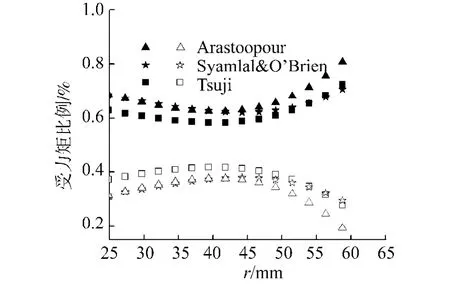
图11 91.2 mm时床高颗粒所受力矩比例分布Fig.11 Proportion of torque adding to particles at vessel height of 91.2 mm

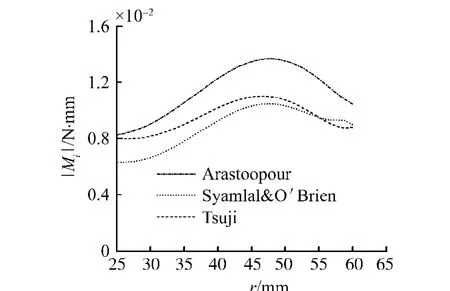
图12 91.2 mm时床高颗粒所受滚动摩阻力矩分布Fig.12 The profile of torque at vessel height of 91.2 mm

图11给出的是环隙区91.2 mm床高上颗粒所受滚动摩阻力矩和切向接触力矩比例分布，由图可以看出，在环隙区滚动摩阻力矩要大于切向接触力矩，由此更能说明，在矩形喷动床DEM模拟中加入滚动摩阻力矩的必要性.图12是91.2 mm床高近壁面处滚动摩阻力矩分布，由图可见随r(r＞25 mm区域)的增大，颗粒所受滚动摩阻力矩增大，Arastoopour模型的预测值最大，Syamlal＆O＇Brien模型预测值最小，Tsuji模型介于两者之间，这与图9中减速区颗粒速度梯度变化趋势相同，即Arastoopour模型梯度最大，Tsuji模型次之，Syamlal＆O＇Brien模型最小，滚动摩阻力矩与速度梯度两者之间的关系类似于牛顿流体中粘性应力和变形速率之间的关系，这说明在颗粒间相互作用中，滚动摩阻力矩既可以是的驱动力也可以是阻力.由图9和图12还可看出:vz峰值出现先于Mi峰值，这说明在相互影响关系上，速度梯度起主导作用.

3 结论

文中分别采用 Arastoopour、Di Felice、Syamlal＆O＇Brien和Tsuji模型结合DEM(pseudo－three－dimensional)方法对矩形喷动床内颗粒运动进行了模拟，并与赵香龙等人的实验结果比较分析得出如下结论:

1)Arastoopour、Syamlal＆O＇Brien和Tsuji模型均可预测矩形喷动床内的流动结构.

2)Arastoopour、Syamlal＆O＇Brien和Tsuji模型对颗粒轴向速度的预测在趋势上均与赵香龙等人实验结果相符，其中Tsuji模型的预测值与实验结果最为接近.

3)在环隙区内，颗粒碰撞频率增加导致了vz的增大.滚动摩阻力矩的加入使得环隙区内颗粒轴向速度最大值的预测更加精确，而且模拟结果显示该区内滚动摩阻力矩大于切向接触力矩，因此在喷动床DEM模拟中加入滚动摩阻力矩很有必要.

4)滚动摩阻力矩与颗粒速度梯度两者之间是相互作用的，速度梯度起主导作用.

［1］金涌，祝京旭，汪展文.流态化工程原理［M］.北京:清华大学出版社，2001:360－362.

［2］DU Wei，BAO Xiaojun.Computational fluid dynamics (CFD)modeling of spouted bed:assessment of drag coefficient correlations［J］.Chemical Engineering Science，2006，61(5):1401－1420.

［3］LI Jie，KUIPERS J A M.Gas－particle interactions in dense gas－fluidized beds［J］.Chemical Engineering Science，2003，58(3－6):711－718.

［4］TSUJI Y，KAWAGUCHI T，TANAKA T.Discrete particle simulation of two－dimensional fluidized bed［J］.Powder Technology，1993，77:79－87.

［5］ZHONG W Q，XIONG Y Q.DEM simulation of gas－solid flow behaviors in spout－fluid bed［J］.Chemical Engineering Science，2006，61:1571－1584.

［6］ARASTOOPOUR H，PAKDEL P，ADEWUMI M.Hydrodynamic analysis of dilute gas－solids flow in a vertical pipe［J］.Powder Technology，1990:62(2):163－170.

［7］Di FELICE R.The voidage functions for fluid－particle inter－action system［J］.International Journal of Multiphase Flow，1994，20(1):153－159.

［8］SYAMLAL M，O＇BRIEN T J.Simulation of granular layer inversion in liquid fluidized beds［J］.International Journal of Multiphase Flow，1988，14(4):473－481.

［9］ZHOU Y C，WRIGHT B D，YANG R Y.Rolling friction in the dynamic simulation of sandpile formation［J］.Physica A—Statistical Mechanics and its Applications，1999，269: 536－553.

［10］XU B H，YU A B.Numerical simulation of the gas－solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics［J］.Chemical Engineering Science，1997，52:2785－2809.

［11］ZHAO X L，LI S Q，LIU G Q.DEM simulation of the particle dynamics in two－dimensional spouted beds［J］.Powder Technology，2008，184:205－213.

［12］LIM C J，MATHUR K B.Modeling of particle movement in spouted beds［M］.Cambridge:Cambridge University Press，1978:104－109.

［13］HE Y L，LIM C J，GRACE J R，ZHU J X，QZN S Z.Measurements of voidage profiles in spouted beds［J］.Canadian Journal of Chemical Engineering，1994，72(4):229－234.

［14］HE Y L，QIN S Z，LIM C J，GRACE J R.Particle velocity profiles and solid flow patterns in spouted beds［J］.Canadian Journal of Chemical Engineering，1994，72(8):561－568.

［15］MATHUR K B，EPSTEIN N.Spouted Beds［M］.New York:Academic Press，1974:265－270.

［16］SAN JOSÉ M J，MARTIN O，ALVAREZ S，IZQUIERDO M A，BILBAO J.Solid cross－flow into the spout and particle trajectories in conical spouted beds［J］.Chemical Engineering Science，1998，53(20):3561－3570.

［17］ZHAO X L，YAO Q，LI S Q.Effects of draft tubes on particle velocity profiles in spouted beds［J］.Chemical Engineering and Technology，2006，29(7):875－881.

［18］张勇，金保升，钟文琪.基于颗粒尺度DEM直接数值模拟的喷动流化床颗粒运动特性［J］.东南大学学报:自然科学版，2008，38(1):110－115.

ZHANG Yong，JIN Baosheng，ZHONG Wenqi.Particlescale based DEM simulation of particle motion spout－fluid bed［J］.Journal of Southeast University:Natural Science E－dition，2008，38(1):110－115.

［19］KAWAGUCHI T，SAKAMOTO M，TANAKA T.Quasithree－dimensional numerical simulation of spouted beds in cylinder［J］.Powder Technology，2000，109(1):3－12.